E-Jurnal Matematika Vol. 10(2), Mei 2021, pp. 74-80

DOI: https://doi.org/10.24843/MTK.2021.v10.i02.p324

ISSN: 2303-1751

PERAMALAN INDEKS HARGA PROPERTI RESIDENSIAL MENGGUNAKAN METODE BAYES

Putu Gde Budha Wiryadana1§, I Wayan Sumarjaya2, I Komang Gde Sukarsa3

§Corresponding Author

ABSTRACT

Residential property is a property in the form of building which serves as residence or house. House has function as a place whether to take a rest, to take cover and to get together with family. Residential property price indices (RPPIs) forecasting has aim as a development planning by the developer to avoid shortages or excess of home supplies. This research aims to model and predict the RPPIs using the Bayes method for 2020 to 2021. The data used in this research is the data from RPPIs of Denpasar city from 2012 in the first quarter to 2019 in the fourth quarter. Then, the method which is used is Bayes method with autoregression (AR) model in forecasting RPPIs. Therefore, it obtained mean absolute percentage error (MAPE) for forecasting the next one period with ( ÷ )

equal to 0,4049416%. For the result of RPPIs forecasting in Denpasar city from 2020 the first quarter to 2021 the fourth quarter has an insignificant increase with an average difference for each quarter increased by 0,3568%.

Keywords: Autoregressive Model, Bayes Method, Forecasting, Markov Chain Monte Carlo, Residential Property Price Indices

  • 1.    PENDAHULUAN

Properti adalah investasi dalam bentuk aset fisik berupa kepemilikan tanah dan bangunan yang mencakup sarana dan prasarana yang ada di dalamnya (Wulandari, 2017). Industri properti sangat sulit untuk diprediksi dan memiliki risiko yang cukup tinggi. Permintaan masyarakat terhadap industri properti sulit diprediksi karena ketika pertumbuhan ekonomi tinggi menyebabkan permintaan meningkat dan pihak pengembang cenderung over supplied, namun ketika pertumbuhan ekonomi mengalami penurunan menyebabkan permintaan menurun drastis. Risiko tinggi disebabkan sumber dana utama dari industri properti berasal dari bank, proyek beroperasi dengan menggunakan aktiva tetap berupa tanah dan bangunan, dan dalam pembebasan lahan membutuhkan modal yang cukup besar (Rifai, 2015).

Menurut Evans & Evans (2007) properti residensial adalah bentuk properti berupa bangunan yang berfungsi sebagai tempat tinggal atau rumah. Permintaan properti

residensial terus meningkat seiring meningkatnya jumlah populasi manusia.

Perkiraan indeks harga properti residensial (IHPR) untuk waktu yang akan datang penting dilakukan untuk meminimalisir kecenderungan over supplied. Peramalan IHPR berguna bagi pengembang dalam merencanakan pembangunan dan untuk melihat inflasi yang akan digunakan pemerintah dalam membuat kebijakan ekonomi.

Analisis deret waktu merupakan salah satu analisis dalam statistika yang berguna dalam membuat peramalan menghasilkan galat yang kecil. Ada beberapa metode dalam peramalan statistika, seperti ARIMA, Bayes, pemulus exponensial, dan lain-lain. Penelitian Amry (2018) tentang pendekatan Bayes model autoregressive moving average (ARMA) untuk peramalan inflansi di Indonesia menunjukkan bahwa hasil dari peramalan Bayes lebih dekat dengan data faktual daripada peramalan deret waktu model ARMA. Jacobson & Karlsson (2002) menggunakan metode Bayesian model averaging (BMA) untuk peramalan inflasi indeks harga konsumen Swedia, menghasilkan

perkiraan yang kuat dengan mean square error (MSE) yang kecil dari setiap model yang disertakan.

Statistika Bayes menerapkan teori peluang tentang kepercayaan terhadap suatu peristiwa yang didasarkan pada pengetahuan dari percobaan sebelumnya atau kepercayaan individual (Bernardo & Smith, 1994). Statistika Bayes untuk peramalan, melibatkan pengondisian pada informasi yang diketahui untuk membuat pernyataan tentang informasi yang tidak diketahui Geweke & Whiteman (2006). Penelitian ini menggunakan statistika Bayes sebagai pendekatan untuk memodelkan dan meramalkan IHPR dari tahun 2020 sampai tahun 2021 dengan harapan dapat menghasilkan galat yang sekecil mungkin.

  • 2.    METODE PENELITIAN

    • 2.1    Jenis dan Sumber Data

Data yang digunakan dalam penelitian ini adalah data sekunder, yaitu data indeks harga properti residensial triwulanan untuk wilayah Denpasar tahun 2012 hingga 2019 yang dipublikasikan oleh Bank Indonesia. Penelitian ini menggunakan data indeks harga properti residensial (Y = { Yt}) sebagai variabel terikat dan data indeks harga properti residensial n periode sebelumnya X = { Yt _1 ,Yt _2,.,Yt _ n} dengan n merupakan orde dari model autoregresif (AR) yang ditentukan dari nilai AIC terkecil sebagai variabel bebas.

  • 2.2    Metode Analisis Data

Metode analisis data pada penelitian ini menggunakan metode Bayes dengan bantuan program R 4.0.1. Adapun langkah-langkah yang dilakukan sebagai berikut:

  • 1.    Plot data indeks harga properti residensial untuk melihat adanya tren pada data.

  • 2.    Menentukan orde AR(n) dalam pemilihan nilai n dengan AIC terkecil untuk n = {1,2.....10}.

  • 3.    Memilih  prior untuk masing-masing

parameter.

  • a.    Prior  normal untuk mengestimasi

parameter β dalam persamaan yi = βxi + εi, εi~N0O, σ2).

  • b.    Prior gamma untuk mengestimasi paramater   σ2   dalam persamaan

yi = βxi + εi, εi~N(0,σ2)

  • 4.    Menghitung nilai posterior dari masing-masing prior.

    6.


  • 5.    Menghitung nilai estimasi parameter dan peramalan dengan metode MCMC menggunakan Algoritme Gibbs Sampling.

  • a.    Menentukan nilai mean dan variance

dari distribusi posterior untuk parameter β menggunakan 2 (dua) persamaan, yaitu

M= = fa 1+ fa{Xt)~1 (∑_ 1β0 + ⅛XlYt) dan

V = = (∑_ 1 + ⅛X'Xt) _ 1.

  • b.    Menghitung estimasi parameter β dengan membangun bilangan acak berdistribusi normal dengan nilai mean dan variance dari langkah (5a) sesuai persamaan x = μ + zσ (z merupakan bilangan acak berdistribusi normal dengan mean = 0 dan variance = 1).

  • c.    Menentukan nilai parameter bentuk dan parameter laju dari distribusi posterior untuk parameter      menggunakan

persamaan T1 = T0 + T dan θ 1 = 00 + (Y — βXt) (Y — β Xt)  (menggunakan

nilai awal T0 = 1 dan θ 0 = 0,1).

  • d.    Menghitung estimasi parameter dengan membangun bilangan acak menggunakan persamaan σ 2 = O1 /(z'z) dari penduga untuk parameter

    e.


    f.


    g.


    h.


Menghitung estimasi indeks harga

untuk p periode selanjutnya menggunakan persamaan Yt+p = a + βl Yt+(p _ 1 ) + ■■’ + βn Yt+{_ - p') + ( σ V ). Mengulang langkah 5a sampai 5e sebanyak kali (pada kasus ini

menggunakan M = 15.000 kali) untuk mendapatkan iterasi {β 1,.,.,βu}, {(σ 2) 1,.,(σ 2)m}, dan

{( Yt+1, .,Yt+p) ,.,( Yt+1, .,Yt+p) }■

Membuang sebanyak    kali (pada

kasus ini menggunakan N = 5.000 kali) iterasi awal (burn-in) karena sampel dari iterasi awal bukan dari nilai posterior target.

Menghitung nilai rata-rata dari proses iterasi ke-(N + 1) sampai iterasi ke-M.

Menghitung keakuratan dari hasil peramalan menggunakan mean absolute percentage error (MAPE) sesuai persamaan MAPE = Q∑(- 11“^|) ×

100%. '

7. Interpretasi hasil.


  • 3.    HASIL DAN PEMBAHASAN

Bagian ini membahas penerapan metode Bayes untuk meramalkan IHPR Kota Denpasar. Untuk hasil plot data IHPR Kota Denpasar dijelaskan oleh Gambar 1.

Indeks Harga Properti Residensial


Tahun

2012              2014              2016           2018        2020

Gambar 1. Plot Data IHPR Kota Denpasar dari tahun 2012 – 2019

Gambar 1 menunjukkan tren, kenaikan IHPR secara signifikan terjadi dari tahun 2012 hingga tahun 2017 dan dari tahun 2017 hingga tahun 2019 mengalami kenaikan namun tidak terlalu signifikan. Selanjutnya didekati dengan model AR dengan pemilihan nilai AIC terkecil untuk penentuan model terbaik agar menghasilkan galat yang minimum.

  • 3.1    Pemilihan Model Terbaik

Penentuan model terbaik berguna dalam pendekatan data peramalan dengan data faktual agar galat yang dihasilkan diharapkan sekecil mungkin (Tsay, 2010). Dalam pemilihan model AR(n), orde n yang dipilih merepresentasikan sebanyak n-periode sebelumnya dari variabel terikat ( Yt). Perhitungan nilai AIC dari model AR(n) disajikan dalam Tabel 1.

Berdasarkan Tabel 1 nilai AIC terkecil ada pada AR(4) = 139,7227. Oleh karena itu analisis data selanjutnya akan menggunakan model AR(4). Dari model AR(4) dibentuk variabel bebas untuk data indeks harga properti residensial menggunakan empat periode sebelumnya,

(X = { Yt _ 1,Yt _ 2, Yt _ 3 ,Yt - 4} )

dan model regresi yang dibentuk sebagai berikut,

Yt = a + βιYt - 1 + β2 Yt - 2

+ β3 Yt - 3 + β4 Yt -4

+ ⅛             (1)

Tabel 1. Nilai AIC data IHPR Kota

Denpasar untuk orde n = {1,2, ..,10}

Orde AR

Nilai AIC

1

147,7868

2

147,9106

3

146,6744

4

139,7227

5

141,2335

6

142,4288

7

144,3036

8

146,1872

9

148,1775

10

150,1641

  • 3.2    Estimasi Parameter

Estimasi parameter bertujuan untuk menghitung nilai parameter pada model indeks harga properti residensial. Model yang diperoleh diharapkan dapat menghitung perkiraan dengan hasil mendekati nilai sebenarnya.

3.2.1 Estimasi untuk Parameter β

Dalam mencari estimasi nilai untuk parameter β menggunakan prior normal yang dipadukan dengan fungsi likelihood menghasilkan posterior berdistribusi normal dengan mean dan variance sesuai persamaan


M * = (∑0- 1+ ^Xl Xt)1 (∑o 1∕0 +


Distribution of Beta2


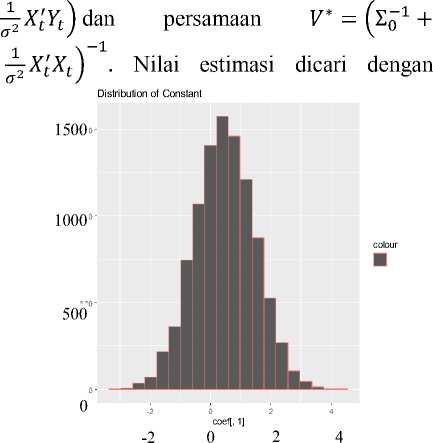
menggunakan perhitungan MCMC algoritme Gibbs sampling (Blake & Mumtaz, 2017). Iterasi yang digunakan sebanyak 15.000 kali karena pada proses Gibbs sampling memerlukan jumlah iterasi yang besar agar konvergensi ke target posterior tercapai dan 5.000 burn-in periode dipilih karena sampel dari iterasi awal bukan dari nilai posterior target, estimasi untuk parameter β ditunjukan pada Gambar 2,


Distribution of Beta1


1500 00


000

1000


500

500


colour


1500500


1000

1000


500

500


0


-0.5


colour


.6

0.9

1.5

.6

0

0   0.

1.2 coef[, 2]

1500

1000

500

(d)

0,0        0,4       0,8


0


-0,5


0.0

coef[, 3]

(c)

0,0


.0

.0

0

0.5                        1.


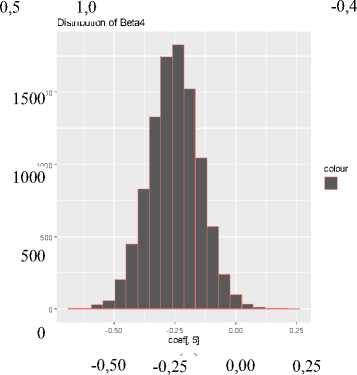
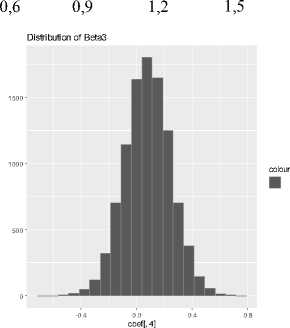
Gambar 2. Plot histogram dari bilangan acak yang dibangun untuk konstata (a) untuk parameter /J1 (b) untuk


parameter (c) untuk parameter (d) dan untuk parameter (e) (Lanjutan)


Gambar 2 menunjukkan distribusi posterior untuk parameter β , dapat dilihat pada pola sebaran data untuk semua parameter yang dibangun berdistribusi normal karena membentuk lonceng simetris. Estimasi parameter dihitung berdasarkan nilai rataan dari bilangan acak yang dibentuk dalam proses MCMC algoritme Gibbs sampling. Simpulan dari rataan untuk parameter β disajikan pada Tabel 2.

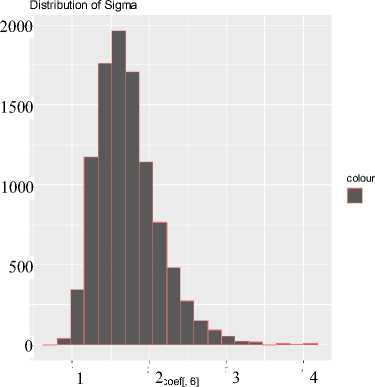
Gambar 3. Plot histogram dari bilangan acak yang dibangun untuk parameter σ2


Tabel 2 Rataan nilai estimasi parameter

Parameter

Estimasi

a

0,47720396

βl

1,07715680

β2

0,09386742

β3

0,07991582

β4

-0,25220898


Sehingga model regresi yang dibentuk untuk data indeks harga properti residensial Kota Denpasar adalah

Yt = 0,47720396

+ 1,07715680Yt-I

+ 0,09386742Yt-2 + 0,07991582Yt-3 - 0,25220898Yt-4 + Zt .                    (2)

  • 3.2.2 Estimasi Untuk Parameter σ2

Dalam mencari estimasi nilai untuk σ2 menggunakan prior inverse gamma atau parameter 1⁄σ2 menggunakan prior gamma yang dipadukan dengan fungsi likelihood menghasilkan posterior berdistribusi gamma dengan shape dan rate sesuai persamaan Tr =   +T dan persamaan ^l =   +

(Y- βxt ) ' (Y- βxt). Nilai estimasi dicari dengan menggunakan perhitungan MCMC algoritme Gibbs sampling (Blake & Mumtaz, 2017). Iterasi yang digunakan sebanyak 15.000 kali karena pada proses Gibbs sampling memerlukan jumlah iterasi yang besar agar konvergensi ke target posterior tercapai dan 5.000 burn-in periode dipilih karena sampel dari iterasi awal bukan dari nilai posterior target ditunjukan pada Gambar 3,

Gambar 3 menunjukkan distribusi posterior untuk parameter σ2 . Rataan untuk parameter σ2 dari bilangan acak yang dibangun adalah 1,72301534. Sehingga model yang dibentuk untuk peramalan dari estimasi parameter β dan parameter σ2 dengan estimasi galat adalah, ^t+ι = 0,47720396

+ 1,07715680Yt

+ 0,09386742Yt.1

+ 0,07991582Yt-2

- 0,25220898Yt-3

+ (√1,72301534

×V∗).

(3)

  • 3.3    Hasil Peramalan

Hasil peramalan diperoleh berdasarkan model yang dibentuk dari distribusi posterior pada parameter β dan parameter σ2 . Berdasarkan model yang dijelaskan pada persamaan (3) untuk peramalan satu periode selanjutnya diperoleh hasil peramalan memiliki nilai MAPE sebesar 0,4049416% disajikan pada Tabel 3.

Tabel 3 Hasil peramalan yang dibangun dari model ^+1

Indeks Harga Properti Residensial

190

180

170

variable

5% mean 95%

2014

22016      Ye     2018

2020


Harga Indeks


160


Date

Real

Forecast

1-Jul-2014

178,3430

175,6459

1-Oct-2014

180,6080

179,1255

1-Jan-2015

181,0960

181,4354

1-Apr-2015

182,0740

182,6842

1-Jul-2015

183,2020

183,0522

1-Oct-2015

183,8250

183,8268

1-Jan-2016

184,4870

184,5588

1-Apr-2016

184,7640

185,1739

1-Jul-2016

184,5240

185,2997

1-Oct-2016

185,2620

184,9629

1-Jan-2017

186,6330

185,5905

1-Apr-2017

186,6890

187,0475

1-Jul-2017

185,5870

187,3560

1-Oct-2017

185,3090

186,0977

1-Jan-2018

185,2350

185,3535

1-Apr-2018

185,4380

185,1455

1-Jul-2018

185,4010

185,6130

1-Oct-2018

185,7350

185,6564

1-Jan-2019

185,8650

186,0475

1-Apr-2019

185,9210

186,1648

1-Jul-2019

185,9770

186,2733

1-Oct-2019

186,0320

186,2650

200

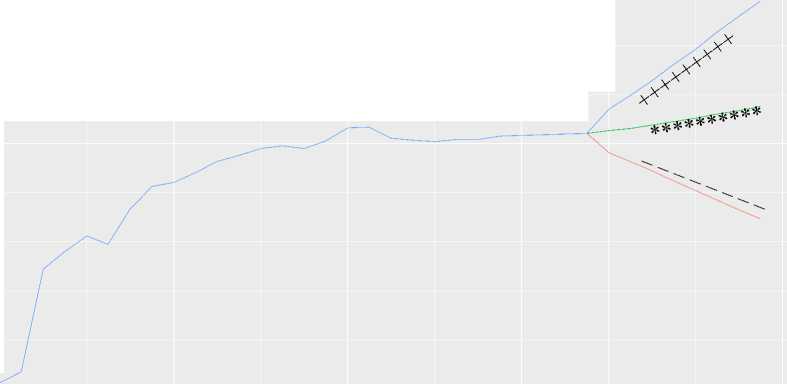
Untuk hasil peramalan dari delapan periode kedepan (dua tahun) berdasarkan persamaan (3) diperoleh hasil peramalan IHPR untuk tahun 2020 triwulan pertama hingga 2021 triwulan keempat berturut-turut sebesar 186,2965; 186,5656; 186,8811; 187,2436; 187,6226; 188,0053; 188,3837; 188,7941. Dengan toleransi minimal (pendekatan interval kredibel 5%) berturut-turut sebesar, 184,0839; 183,2014; 182,2492; 181,2021; 180,2008; 179,2578; 178,2347; dan 177,3323. Toleransi maksimal (pendekatan interval kredibel 95%) berturut-turut sebesar, 188,4823; 189,9175; 191,3523; 193,0604; 194,6424; 196,3396; 197,9562; dan 199,5546.

2022

Tahun

Gambar 4. Plot data hasil peramalan IHPR (***) dengan interval kredibel 5% (– – –) dan 95% (+++)

Dilihat dari Gambar 4 pada rentang interval kredibel dari peramalan satu periode hingga delapan periode selanjutnya menunjukkan bahwa seiring bertambahnya periode maka rentang interval kredibel semakin meluas.

  • 4.    SIMPULAN DAN SARAN

Berdasarkan hasil dan pembahasan, diperoleh model untuk peramalan satu periode selanjutnya yaitu,

= 0,47720396 + 1,07715680Yt

+ 0,09386742Yt-ι

+ 0,07991582Yt-2

- 0,25220898Yt-3

+ (√1,72301534 × v∗).

Hasil peramalan IHPR dari tahun 2020 sampai dengan tahun 2021 mengalami tren naik, dengan rata-rata kenaikan harga sebesar 0,3568% untuk setiap pergantian kuartal. Semakin banyak periode peramalan menyebabkan hasil peramalan menjauhi hasil sebenarnya, terlihat pada interval kredibel yang dibentuk dari peramalan periode pertama hingga kedelapan semakin meluas.

Saran untuk penelitian selanjutnya yaitu diharapkan dapat membangun model yang efektif untuk jangka panjang dan dapat mencoba menggunakan model yang berbeda seperti MA, ARMA, ARIMA, dan lain-lain.

DAFTAR PUSTAKA

Amry, Z. (2018). Bayesian Approach for

Indonesia      Inflation      Forecasting.

International Journal of Economics and Financial Issues, Vol. 8, No. 5, pp. 96– 102.

Bernardo, J. M., & Smith, A. F. M. (1994). Bayesian Theory. Hoboken: John Wiley & Sons, Inc.

Blake, A., & Mumtaz, H. (2017). Applied Bayesian Econometrics for Central Bankers. England: Bank of England. Diakses pada 3 Desember 2019 dari https://www.bankofenngland.co.uk//media /boe/files/ccbs/resources/appliedbayesin-

econometrics-for-centralbankers-update-2017.pdf

Evans, D. L., & Evans, O. W. (2007). The Complete Real Estate Encyclopedia. New York: McGraw-Hill.

Geweke, J., & Whiteman, C. (2006). Bayesian Forecasting. Netherlands: Elsevier B.V.

Jacobson, T., & Karlsson, S. (2002). Finding Good Predictors for Inflation: A Bayesian Model Averaging Approach. Sveriges Riksbank Working Paper Series, Vol. 23, No. 7, pp. 479–496.

Rifai, H. (2015). Pengaruh Risiko Bisnis, Pertumbuhan Perusahaan, Ukuran Perusahaan dan Struktur Aktiva terhadap Kebijakan Hutang pada Perusahaan Sektor Property and Real Estate yang Terdaftar di Bursa Efek Indonesia. Skripsi. Fakultas Ekonomi, Manajemen, Universitas Negeri Yogyakarta, Yogyakarta.

Tsay, R. S. (2010). Analysis of Financial Time Series (Third Edition). Chicago: Wiley.

Wulandari, C. S. (2017). Faktor-Faktor yang Memengaruhi Indeks Harga  Properti

Residensial    Berdasarkan    Tingkat

Pendapatan Negara: Kajian Empiris di 27 Negara. Tesis. Pascasarjana, Ilmu Ekonomi, Institut Pertanian Bogor, Bogor.

80