PERAMALAN PRODUKSI PADI DI KABUPATEN BADUNG, GIANYAR, DAN TABANAN DENGAN METODE VECTOR AUTOREGRESSION (VAR)
on
E-Jurnal Matematika Vol. 10(1), Januari 2021, pp. 32-40
DOI: https://doi.org/10.24843/MTK.2021.v10.i01.p317
ISSN: 2303-1751
PERAMALAN PRODUKSI PADI DI KABUPATEN BADUNG, GIANYAR, DAN TABANAN DENGAN METODE VECTOR
AUTOREGRESSION (VAR)
I Gusti Ayu Meigayoni Lestari1§, I Wayan Sumarjaya2, I Nyoman Widana3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: meigayonilestari29@gmail.com]
-
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id]
-
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: widana@unud.ac.id]
§Corresponding Authors
ABSTRACT
Rice is one of the staple foodstuffs whose availability is very important for public consumption in Indonesia, especially Bali Province. The three regencies that produce the most rice in Bali they are Badung, Gianyar and Tabanan. This study aims to model, predict, and analyze the relationship between rice production in Badung, Gianyar, and Tabanan Regency from January 2018 to December 2019 using vector autoregression (VAR) method. VAR method is a time series method that can be used to model and predict time series with more than one variable simultaneously. The results of this study, namely the VAR model obtained to predict the amount of rice production in Badung, Gianyar, and Tabanan Regencies is third order VAR (VAR (3)). Based on the forecasting criteria for the mean absolute percentage error (MAPE) in this model, a reasonable forecast is obtained for the rice production variables in Badung and Gianyar regencies, and good forecasting for the rice production variables in Tabanan Regency is obtained. Then, based on the granger causality analysis, it is found that the amount of rice production in Gianyar Regency affects the amount of rice production in Badung and Tabanan Regencies, and the amount of rice production in Badung Regency affects the amount of rice production in Gianyar Regency.
Keywords : Granger Causality, Mean Absolute Percentage Error, Rice Production, Vector Autoregression
Peramalan adalah seni dan ilmu untuk memprediksi kejadian pada masa depan dengan melibatkan pengambilan data historis dan memproyeksikannya ke masa mendatang dengan model pendekatan matematis (Heizer et al, 2011). Pada proses peramalan data yang dapat digunakan adalah data deret waktu (time series). Analisis deret waktu dapat dibagi menjadi dua yaitu analisis deret waktu univariate (satu variabel) dan analisis deret waktu multivariate (lebih dari satu variabel). Adapun model deret waktu multivariat yang dapat digunakan yaitu vector autoregression (VAR), analisis fungsi transfer, dan analisis fourier. Model VAR merupakan model deret waktu yang dapat digunakan untuk memodelkan dan meramalkan deret waktu dengan lebih dari satu variabel secara simultan.
Penelitian terkait metode VAR adalah sebagai berikut, Ramli et al (2019) menganalisis produksi perikanan, curah hujan, dan suhu permukaan laut dengan model VAR, diperoleh bahwa suhu permukaan laut memengaruhi produksi perikanan tangkap laut dan curah hujan. Model VAR pada penelitian tersebut digunakan untuk memodelkan variabel dari sektor ekonomi. Selain itu, model VAR juga dapat digunakan untuk meramalkan data kunjungan wisatawan mancanegara, penjualan sepeda motor, dan produksi padi.
Padi merupakan salah satu bahan pangan pokok yang mempunyai pengaruh besar dalam sektor ekonomi. Ketersediaan padi yang stabil menjadi sangat penting karena untuk persediaan dan konsumsi masyarakat sehari-hari di Indonesia, khususnya Provinsi Bali.Menurut BPS Provinsi Bali, pada tahun 2017 jumlah
produksi padi di Bali adalah sebanyak 836.236 ton. Tiga kabupaten yang memproduksi padi terbanyak di Bali adalah Kabupaten Badung sebesar 113.880 ton, Gianyar sebesar 172.987 ton, dan Tabanan sebesar 211.178 ton. Ketiga kabupaten tersebut menyumbang lebih dari 50% total produksi padi di Provinsi Bali. Sehingga ketiga kabupaten tersebut berperan penting dalam memproduksi padi untuk konsumsi masyarakat di Bali.
Proses produksi padi bisa diajalankan apabila persyaratan faktor produksi yang dibutuhkan sudah terpenuhi. Jumlah produksi padi di Kabupaten Badung, Gianyar, dan Tabanan berbeda-beda karena terdapat beberapa faktor yang memengaruhi diantaranya adalah luas lahan, modal, dan tenaga kerja. Selain itu, dalam proses penanaman padi terdapat rintangan berupa serangan organisme pengganggu tumbuhan. Kenyataan yang terjadi dari tahun ke tahun di Kabupaten Badung, Gianyar, dan Tabanan terjadinya penurunan jumlah produksi padi. Penurunan jumlah produksi padi ini diakibatkan karena tingkat penggunaan faktor-faktor produksi yang belum optimal. Sementara itu, dilakukan upaya untuk menanggulangi penurunan jumlah produksi padi di suatu wilayah, dengan cara memenuhi kekurangan tersebut dari jumlah produksi padi wilayah lain yang memiliki produksi lebih optimal.
Berdasarkan uraian di atas, maka penulis tertarik melakukan penelitian memodelkan, meramalkan, dan menganalisis hubungan produksi padi Kabupaten Badung, Gianyar, dan Tabanan dengan menggunakan metode VAR.
Data yang digunakan pada penelitian ini adalah data sekunder, yaitu jumlah produksi padi Kabupaten Badung, Gianyar, dan Tabanan periode Januari 2000 sampai Desember 2017 berupa data empat bulanan yang diperoleh dari Badan Pusat Statistik Provinsi Bali. Analisis data jumlah produksi padi Kabupaten Badung, Gianyar, dan Tabanan menggunakan software Eviews 10 dengan data amatan sebanyak 54 data. Adapun langkah-langkah yang akan dilakukan pada penelitian ini adalah sebagai berikut:
-
1. Melakukan analisis deskriptif terhadap data untuk mengetahui gambaran umum mengenai jumlah produksi padi Kabupaten Badung, Gianyar, dan Tabanan.
-
2. Memilih orde model VAR dengan menggunakan data yang diperoleh berdasarkan kriteria Akaike’s Information Criterion (AIC), Schwarz Information Criterion (SC), atau Hannan-Quinn Criterion (HQ).
-
3. Melakukan estimasi parameter model menggunakan metode multivariate least square (MLS) sesuai dengan orde yang telah diperoleh pada langkah dua.
-
4. Melakukan uji diagnostik model untuk mengecek asumsi-asumsi telah terpenuhi. Asumsi yang harus dipenuhi adalah sebagai berikut :
-
a. Tidak ada autokorelasi pada residual model.
-
b. Residual model menyebar normal.
-
c. Model yang diperoleh merupakan
proses VAR yang stabil.
Jika salah satu asumsi tidak terpenuhi, maka dipilih orde model VAR seperti pada langkah kedua dengan menggunakan kriteria lain yang belum dipilih dari Akaike’s Information Criterion (AIC), Schwarz Information Criterion (SC), dan Hannan-Quinn Criterion (HQ).
-
5. Melakukan proses peramalan jumlah produksi padi Kabupaten Badung, Gianyar, dan Tabanan, serta menghitung nilai mean absolute percentage error (MAPE) untuk mengetahui keakuratan peramalan.
-
6. Melakukan uji kausalitas granger untuk mengetahui hubungan produksi padi di Kabupaten Badung, Gianyar, dan Tabanan.
-
7. Melihat pengaruh perubahan guncangan (shock) jumlah produksi padi di Kabupaten Badung, Gianyar, dan Tabanan dengan menggunakan impulse response function (IRF).
-
8. Melakukan analisis forecast error variance decomposition (FEVD) untuk mengetahui besarnya pengaruh guncangan (shock) dari jumlah produksi padi Kabupaten Badung, Gianyar, dan Tabanan.
Berdasarkan plot pada Gambar 1, dapat dilihat bahwa tidak terdapat tren pada data produksi padi Kabupaten Badung, Gianyar, dan Tabanan.
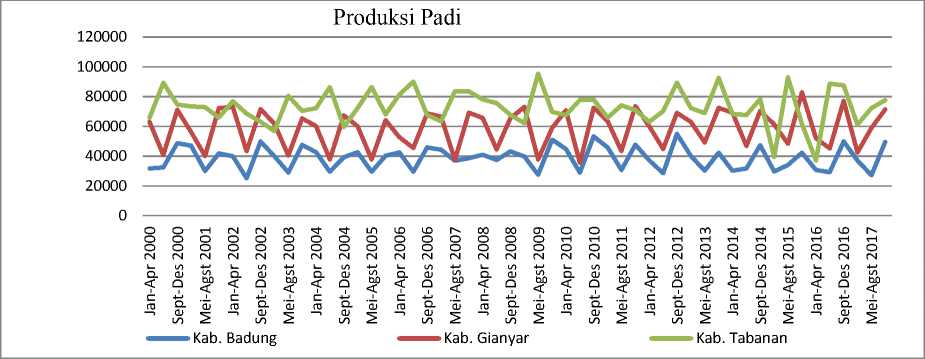
Gambar 1. Plot Data Produksi Padi di Kabupaten Badung, Gianyar, dan Tabanan
Pemilihan orde optimum pada model VAR dapat dilakukan menggunakan AIC, SC, dan HQ.
Tabel 1. Nilai Kriteria AIC, SC, dan HQ
|
Lag |
AIC |
SC |
HQ |
|
0 |
63,40112 |
63,52038 |
63,44579 |
|
1 |
63,09610 |
63,57314 |
63,27481 |
|
2 |
62,23249 |
63,06730 |
62,54521 |
|
3 |
61,42686 |
62,61945 |
61,87361 |
|
4 |
61,65628 |
63,20665 |
62,23706 |
|
5 |
61,89156 |
63,79970 |
62,60636 |
|
6 |
62,06963 |
64,33556 |
62,91846 |
|
7 |
61,92014 |
64,54384 |
62,90300 |
|
8 |
61,92322 |
64,90470 |
63,04010 |
Pemilihan Orde optimum berdasarkan kriteria Akaike’s Information Criterion (AIC), Schwarz Information Criterion (SC), dan Hannan-Quinn Criterion (HQ) masing-masing dipilih dengan nilai terkecil. Dapat dilihat pada Tabel 1, bahwa orde tiga terpilih berdasarkan kriteria uji AIC, SC dan HQ. Setelah orde model dipilih, maka langkah selanjutnya melakukan estimasi parameter.
Diperoleh persamaan estimasi model VAR(3) dengan disimbolkan produksi padi Kabupaten Badung, Gianyar, dan Tabanan berturut-turut adalah ^l , ^2, dan Yβ sebagai berikut:
Γ^ιt 43.922,091 Γ^ιt-ιl Γ^1t-2l Γ^1t-3l
[Y2t] = [8.309,953] + 41 [^2t-l]+A2 [Y2t-2]+A2 [Y2t-2]
b⅛ 199.378,4 ⅛t-ll-¾t-2⅛3t-3J dengan,
A2 :
A2
|
-0,099239 |
-0,218336 |
0,004132 |
|
-0,027514 |
-0,165008 |
0,085912], |
|
-0,316630 |
-0,352243 |
-0,288736 |
|
-0,221090 |
-0,087510 |
0,081455 |
|
-0,148947 |
-0,040776 |
0,092446], |
|
-0,095893 |
-0,385873 |
-0,336520 |
|
0,309491 |
0,134353 |
-0,013828 |
|
[0,469769 |
0,539823 |
0,085237]. |
|
0,336850 |
-0,747875 |
0,120032 |
Diagnostik model dilakukan untuk mengecek asumsi-asumsi yang harus dipenuhi oleh model. Asumsi-asumsi yang harus dipenuhi adalah asumsi tidak terdapat autokorelasi pada residual model, asumsi residual model menyebar normal, dan asumsi model merupakan proses yang stabil.
-
1. Uji Autokorelasi
Uji portmanteau digunakan untuk menguji autokorelasi pada residual model. Data yang digunakan adalah data dari bulan Januari 2000 sampai Desember 2017 dengan jumlah data sebanyak 54 data dan orde optimum yang dipilih adalah tiga. Hal ini berarti lag autokorelasi pada residual yang dapat terbentuk adalah 50.
Diperoleh nilai p-value dari lag 4 sampai 50 lebih dari 0,05 yang sebagian dapat dilihat pada Tabel 2. Karena p-value > 0,05, maka terima hipotesis nol, yang berarti tidak terdapat autokorelasi pada residual model dari lag 4 sampai 50.
Tabel 2. Uji Portmanteau
|
Lag |
Q-stat |
p-value |
|
4 |
16,22769 |
0,0623 |
|
5 |
22,26437 |
0,2205 |
|
48 |
190,2517 |
1,0000 |
|
49 |
191,1259 |
1,0000 |
|
50 |
191,2629 |
1,0000 |
-
2. Uji Kenormalan
Uji kenormalan digunakan untuk mengecek residual model VAR menyebar normal dengan menggunakan uji Lomnicki-Jarque-Bera (LJB).
Tabel 3. Nilai Chi-square Statistik Uji Kenormalan
|
Statistik uji |
Chi-square |
Df |
p-value |
|
skewness (sj) |
2,597907 |
3 |
0,4579 |
|
kurtosis (S4) |
1,192181 |
3 |
0,7549 |
|
LJB |
3,790088 |
6 |
0,7051 |
Karena nilai p-value skewness (s3 ), kurtosis (S4∖ dan LJB lebih dari a = 5%, sehingga tidak cukup bukti untuk menolak hipotesis nol, yang artinya residual model menyebar normal.
-
3. Uji Kestabilan
Uji kestabilan digunakan untuk mengecek kondisi kestasioneran model, karena model VAR yang stabil mengimplikasikan bahwa proses tersebut adalah proses yang stasioner (Lutkepohl, 2005). Kestabilan model dapat dilihat dari akar-akar reverse characteristics polynominal yang berada di dalam lingkaran unit.
Tabel 4. Akar-akar Reverse Characteristics Polynomial
|
Akar |
Modulus |
|
-0,508026 - 0,842847i |
0,984115 |
|
-0,508026 + 0,842847i |
0,984115 |
|
-0,461890 - 0,524855i |
0,699153 |
|
-0,461890 + 0,524855i |
0,699153 |
|
-0,131166 - 0,683567i |
0,696038 |
|
-0,131166 + 0,683567i |
0,696038 |
|
0,595759 - 0,242676i |
0,643289 |
|
0,595759 + 0,242676i |
0,643289 |
|
0,457662 |
0,457662 |
Nilai modulus akar-akar reverse characteristics polynomial pada Tabel 4 berada di dalam lingkaran unit. Hal ini berarti, estimasi model VAR dari data jumlah produksi padi di Kabupaten Badung, Gianyar, dan Tabanan adalah model yang stabil.
Kriteria peramalan yang digunakan untuk menguji keakuratan model dalam meramalkan adalah mean absolute percentage error (MAPE). Diperoleh bahwa nilai MAPE peramalan jumlah produksi padi Kabupaten Badung, Gianyar, dan Tabanan Provinsi Bali berturut-turut adalah 31,73%; 30,38%; dan 14,58%. Berdasarkan kriteria nilai MAPE, maka menunjukkan peramalan jumlah produksi padi di Kabupaten Badung dan Gianyar masuk akal (wajar), serta peramalan jumlah produksi padi di Kabupaten Tabanan yang baik. Hasil peramalan jumlah produksi padi di Kabupaten Badung, Gianyar, dan Tabanan Provinsi Bali dapat diamati dari Tabel 5 sebagai berikut:
Tabel 5. Peramalan Produksi Padi Kabupaten Badung, Gianyar, dan Tabanan
|
Periode |
Peramalan Produksi Padi | ||
|
Kab. Badung |
Kab. Gianyar |
Kab. Tabanan | |
|
Jan-Apr 2018 |
35.484,88 |
52.734,18 |
72.962,79 |
|
Mei-Ags 2018 |
38.588,37 |
58.029,58 |
74.225,55 |
|
Sept-Des 2018 |
41.988,87 |
64.198,53 |
71.428,88 |
|
Jan-Apr 2019 |
35.528,11 |
52.802,06 |
73.047,48 |
|
Mei-Ags 2019 |
38.799,25 |
58.406,94 |
74.111,42 |
|
Sept-Des 2019 |
41.732,73 |
63.749,37 |
71.462,82 |
Setelah diperoleh model VAR yang stabil, akan dilihat variabel mana yang memengaruhi variabel lainnya dengan menggunakan uji kausalitas granger.
Tabel 6. Kausalitas Granger Variabel Dependen Jumlah Produksi Padi Kabupaten Badung
|
Variabel |
F |
p-value |
|
4,17272 |
0,0110 | |
|
Y3 |
0,96722 |
0,4167 |
Berdasarkan Tabel 6 diperoleh bahwa p-value lebih kecil dari 0,05 sehingga keputusannya adalah menolak hipotesis nol, yang berarti jumlah produksi padi Kabupaten Badung signifikan berpengaruh pada jumlah produksi padi Kabupaten Gianyar. Sementara itu, jumlah produksi padi Kabupaten Tabanan
memiliki p-value lebih besar dari 0,05 sehingga keputusannya adalah tidak dapat menolak hipotesis nol, atau jumlah produksi padi Kabupaten Tabanan tidak memiliki pengaruh terhadap jumlah produksi padi Kabupaten Badung.
Tabel 7. Kausalitas Granger Variabel Dependen Jumlah Produksi Padi Kabupaten Gianyar
|
Variabel |
F |
p-value |
|
γi |
3,31073 |
0,0286 |
|
Y3 |
0,94700 |
0,4262 |
Berdasarkan Tabel 7 diperoleh bahwa p-value lebih kecil dari 0,05 sehingga keputusannya adalah menolak hipotesis nol, yang berarti jumlah produksi padi Kabupaten Gianyar signifikan berpengaruh pada jumlah produksi padi Kabupaten Badung. Sementara itu, jumlah produksi padi Kabupaten Tabanan memiliki p-value lebih besar dari 0,05 sehingga keputusannya adalah tidak dapat menolak hipotesis nol, atau jumlah produksi padi Kabupaten Tabanan tidak memiliki pengaruh terhadap jumlah produksi padi Kabupaten Gianyar.
Tabel 8. Kausalitas Granger Variabel Dependen Jumlah Produksi Padi Kabupaten Tabanan
|
Variabel |
F |
p-value |
|
Yi |
0,63705 |
0,5952 |
|
Y2 |
3,14761 |
0,0343 |
Berdasarkan Tabel 8 diperoleh bahwa p-value lebih besar dari 0,05 sehingga keputusannya adalah tidak dapat menolak hipotesis nol, yang berarti jumlah produksi padi Kabupaten Badung tidak memiliki pengaruh terhadap jumlah produksi padi Kabupaten Tabanan. Sementara itu, jumlah produksi padi Kabupaten Badung memiliki p-value lebih kecil dari 0,05 sehingga keputusannya menolak hipotesis nol, atau jumlah produksi padi Kabupaten Gianyar signifikan berpengaruh pada jumlah produksi padi Kabupaten Tabanan.
Pada analisis IRF, dilihat satu respon dalam menanggapi shock yang diberikan oleh variabel lain. Fungsi respon impuls dari jumlah produksi padi Kabupaten Badung, Gianyar, dan Tabanan selama 10 periode sebagai berikut:
Response of Y1 to Y2 Innovation using Cholesky (d.f. adjusted) Factors
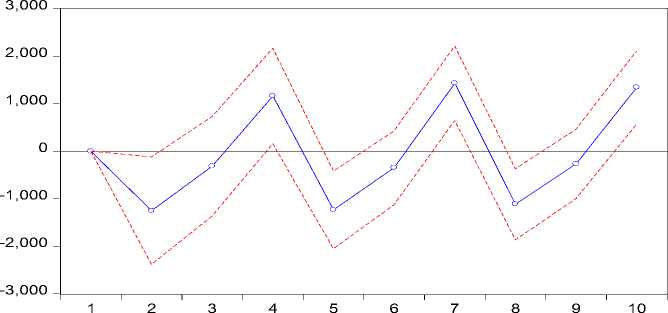
Gambar 2. Plot IRF Jumlah Produksi Padi Kabupaten Badung terhadap Jumlah Produksi Padi Kabupaten Gianyar
Berdasarkan Gambar 2 terlihat adanya pengaruh negatif pada jumlah produksi padi Kabupaten Badung setelah periode satu sampai periode ketiga, setelah periode kelima sampai periode keenam dan setelah periode kedelapan sampai periode kesembilan karena
adanya shock dari jumlah produksi padi Kabupaten Gianyar. Jumlah produksi padi Kabupaten Badung menunjukkan pengaruh positif pada periode keempat, periode ketujuh, dan periode kesepuluh.
Response of Y1 to Y3 Innovation using Cholesky (d.f. adjusted) Factors
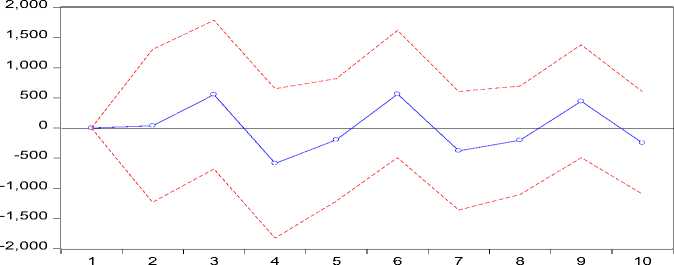
Gambar 3. Plot IRF Jumlah Produksi Padi Kabupaten Badung terhadap Jumlah Produksi Padi Kabupaten Tabanan
Berdasarkan Gambar 3 terlihat adanya pengaruh positif pada jumlah produksi padi Kabupaten Badung setelah periode satu sampai periode ketiga, periode keenam dan periode kesembilan karena adanya shock dari
jumlah produksi padi Kabupaten Tabanan. Jumlah produksi padi Kabupaten Badung menunjukkan pengaruh negatif setelah periode keempat sampai periode kelima, dan setelah periode ketujuh sampai periode kedelapan.
Response of Y2 to Y1 Innovation using Cholesky (d.f. adjusted) Factors
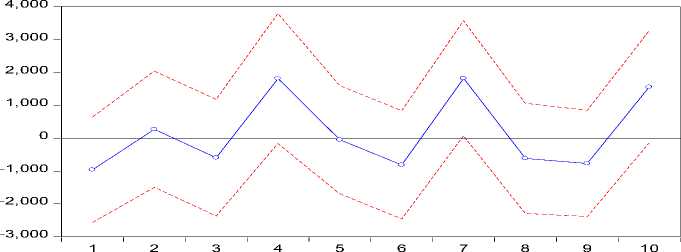
Gambar 4. Plot IRF Jumlah Produksi Padi Kabupaten Gianyar terhadap Jumlah Produksi Padi Kabupaten Badung
Berdasarkan Gambar 4 terlihat adanya pengaruh negatif pada jumlah produksi padi Kabupaten Gianyar periode satu, periode ketiga, setelah periode kelima sampai periode keenam, dan setelah periode kedelapan sampai periode kesembilan karena adanya shock dari
jumlah produksi padi Kabupaten Badung. Jumlah produksi padi Kabupaten Gianyar menunjukkan pengaruh positif pada periode kedua, periode keempat, periode ketujuh, dan periode kesepuluh.
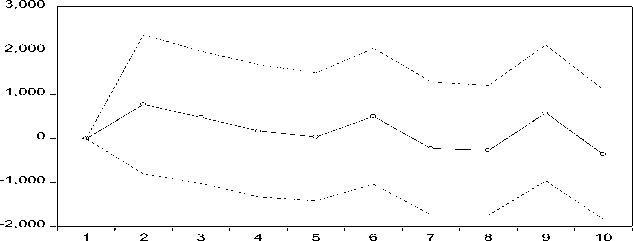
Response of Y2 to Y3 Innovation using Cholesky (d.f. adjusted) Factors
Gambar 5. Plot IRF Jumlah Produksi Padi Kabupaten Gianyar terhadap Jumlah Produksi Padi Kabupaten Tabanan
Berdasarkan Gambar 5 terlihat adanya pengaruh positif pada jumlah produksi padi Kabupaten Gianyar setelah periode satu sampai periode keenam, dan periode kesembilan karena adanya shock dari jumlah
produksi padi Kabupaten Tabanan. Jumlah produksi padi Kabupaten Gianyar menunjukkan pengaruh negatif setelah periode ketujuh sampai periode kedelapan, dan periode kesepuluh.
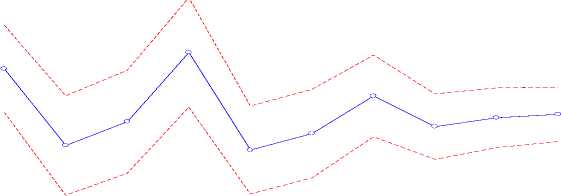
Response of Y3 to Y1 Innovation using Cholesky (d.f. adjusted) Factors
8,000
6,000
4,000
2,000
0
-2,000
-4,000
-6,000
1 2 3 4 5 6 7 8 9 10
Gambar 6. Plot IRF Jumlah Produksi Padi Kabupaten Tabanan terhadap Jumlah Produksi Padi Kabupaten Badung
Berdasarkan Gambar 6 terlihat adanya pengaruh positif terhadap jumlah produksi padi Kabupaten Tabanan pada periode satu, periode keempat, dan periode ketujuh karena adanya shock dari jumlah produksi padi Kabupaten Badung. Jumlah produksi padi
Kabupaten Tabanan menunjukkan pengaruh negatif setelah periode kedua sampai periode ketiga, setelah periode kelima sampai periode keenam, dan setelah periode kedelapan sampai periode kesepuluh.
Response of Y3 to Y2 Innovation using Cholesky (d.f. adjusted) Factors
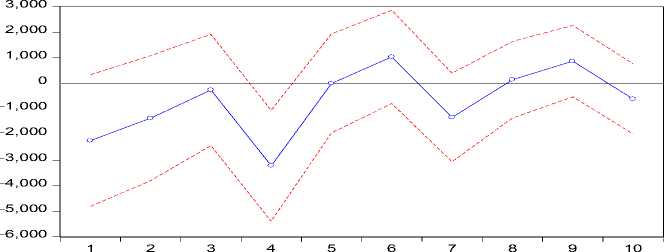
Gambar 7. Plot IRF Jumlah Produksi Padi Kabupaten Tabanan terhadap Jumlah Produksi Padi Kabupaten Gianyar
Berdasarkan Gambar 7 terlihat adanya pengaruh negatif pada jumlah produksi padi Kabupaten Tabanan setelah periode satu sampai periode keempat, periode ketujuh dan periode kesepuluh karena adanya shock dari jumlah produksi padi Kabupaten Gianyar. Jumlah produksi padi Kabupaten Tabanan menunjukkan pengaruh positif setelah periode kelima sampai periode keenam, dan setelah periode kedelapan sampai periode kesembilan.
Analisis FEVD dalam model VAR bertujuan untuk memprediksi kontribusi persentase varians setiap variabel karena adanya guncangan (shock) dari variabel lain. Berdasarkan Tabel 8, Tabel 9, dan Tabel 10 dapat diamati besarnya kontribusi dari setiap variabel jumlah produksi padi Kabupaten Badung, Gianyar, dan Tabanan Provinsi Bali selama 10 periode.
Tabel 9. Variance Decomposition Jumlah Produksi Padi Kabupaten Badung
|
Periode |
Y2 |
Y3 | |
|
1 |
100,0000 |
0,000000 |
0,000000 |
|
2 |
93,19563 |
6,798294 |
0,006076 |
|
3 |
91,78588 |
6,933896 |
1,280225 |
|
4 |
86,66006 |
10,97570 |
2,364231 |
|
5 |
82,08917 |
15,55304 |
2,357787 |
|
6 |
80,99729 |
15,63456 |
3,368157 |
|
7 |
75,85975 |
20,61693 |
3,523323 |
|
8 |
73,15687 |
23,35569 |
3,487443 |
|
9 |
72,64854 |
23,32664 |
4,024821 |
|
10 |
69,38392 |
26,69025 |
3,925827 |
Berdasarkan Tabel 9 dapat dilihat bahwa kontribusi terbesar terhadap variabel jumlah produksi padi Kabupaten Badung adalah variabel itu sendiri dengan kontribusi yang diberikan selama 10 periode adalah 69,38%-100%. Kemudian kontribusi terbesar kedua diberikan oleh jumlah produksi padi Kabupaten Gianyar yang mencapai 26,69% dan sementara itu, jumlah produksi padi Kabupaten Tabanan memberikan hanya sedikit kontribusi dalam jumlah produksi padi Kabupaten Badung.
Tabel 10. Variance Decomposition Jumlah Produksi Padi Kabupaten Gianyar
|
Periode |
Y1 |
Y2 |
Y3 |
|
1 |
2,786320 |
97,21368 |
0,00000 |
|
2 |
2,838271 |
95,44512 |
1,716612 |
|
3 |
3,774403 |
93,89344 |
2,332160 |
|
4 |
9,602340 |
88,60308 |
1,794579 |
|
5 |
8,815315 |
89,53527 |
1,649416 |
|
6 |
9,840726 |
88,07020 |
2,089077 |
|
7 |
13,70939 |
84,42011 |
1,870499 |
|
8 |
13,30476 |
84,84964 |
1,845595 |
|
9 |
13,95085 |
83,73531 |
2,313841 |
|
10 |
15,72914 |
82,01983 |
2,251026 |
Berdasarkan Tabel 10 dapat dilihat bahwa kontribusi terbesar terhadap variabel produksi
padi Kabupaten Gianyar adalah variabel itu sendiri dengan kontribusi yang diberikan selama 10 periode adalah 82,02%-97,21%. Kemudian kontribusi terbesar kedua diberikan oleh produksi padi Kabupaten Badung yang mencapai 15,73% dan sementara itu, produksi padi Kabupaten Tabanan memberikan sedikit kontribusi dalam produksi padi Kabupaten Gianyar hanya mencapai 2,25%.
Tabel 11. Variance Decomposition Jumlah Produksi Padi Kabupaten Tabanan
|
Periode |
Y1 |
Y2 |
Y3 |
|
1 |
8,124306 |
5,286241 |
86,58945 |
|
2 |
10,65090 |
6,396826 |
82,95227 |
|
3 |
10,19625 |
6,065255 |
83,73850 |
|
4 |
18,06376 |
12,09834 |
69,83790 |
|
5 |
20,68286 |
11,65895 |
67,65819 |
|
6 |
21,16754 |
12,11326 |
66,71921 |
|
7 |
21,54736 |
13,02113 |
65,43152 |
|
8 |
21,84752 |
12,98194 |
6517054 |
|
9 |
21,76629 |
13,40174 |
64,83197 |
|
10 |
21,71094 |
13,60320 |
64,68586 |
Berdasarkan Tabel 11 dapat dilihat bahwa kontribusi terbesar terhadap variabel produksi padi Kabupaten Tabanan adalah variabel itu sendiri dengan kontribusi yang diberikan selama 10 periode adalah 64,69%-86,59%. Kemudian kontribusi terbesar kedua diberikan oleh produksi padi Kabupaten Badung yang mencapai 21,85% dan sementara itu, produksi padi Kabupaten Gianyar memberikan sedikit kontribusi dalam produksi padi Kabupaten Tabanan mencapai 13,60%.
Estimasi model VAR yang terbentuk adalah model VAR(3) untuk produksi padi Kabupaten Badung, Gianyar, dan Tabanan berturut-turut adalah ^l , ^2 , dan Y^ sebagai berikut:
pit 43922,091 Γ^ιt-ιl Γ^ιt-2l Γ^ιt-3l [Y2t] = [8309,953] + A1 [Y2t-1]+Λ2 [¾t-2]+A3 [Y2t-3]
LY3t 199378,4 Y3t-1⅛-it-2
dengan,
-0,099239 A1 = [-0,027514 -0,316630
-
-
-
0,218336
0,165008
0,352243
0,004132 0,085912], -0,288736
2
-0,221090 [-0,148947
-0,095893 0,309491
[0,469769
0,336850
-0,087510
-0,040776
-0,385873 0,134353
0,539823
-0,747875
0,081455
0,092446
-0,336520
-0,013828
0,085237] 0,120032
Diperoleh bahwa nilai MAPE peramalan jumlah produksi padi Kabupaten Badung, Gianyar, dan Tabanan Provinsi Bali berturut-turut adalah 31,73%; 30,38%; dan 14,58%. Berdasarkan kriteria nilai MAPE, hasil menunjukkan peramalan jumlah produksi padi di Kabupaten Badung dan Gianyar masuk akal (wajar), serta peramalan jumlah produksi padi di Kabupaten Tabanan yang baik.
Berdasarkan analisis kausalitas granger, diperoleh jumlah produksi padi Kabupaten Gianyar memengaruhi jumlah produksi padi Kabupaten Badung dan Tabanan, serta jumlah produksi padi Kabupaten Badung memengaruhi jumlah produksi padi Kabupaten Gianyar.
DAFTAR PUSTAKA
Bali, B. (2019). Dipetik Agustus 6, 2019, dari
Statistik Produksi Padi di Bali 2015: https://bali.bps.go.id/dynamictable/2018/0 1/26/184/produksi-padi-provinsi-bali-menurut-kabupaten-kota-2000-2015.html
Budiarti, R. (2018). Analisis Produksi Padi di Kebupaten Sleman. Skripsi. Yogyakarta: Fakultas Ekonomi, Universitas Islam Indonesia.
Dianingsari, K. (2007). Analisis Hubungan Dinamis Suku Bunga SBI, IHSG, dan Suku Bunga Internasional dengan Model Vector Autoregressive. Bogor: Fakultas MIPA, Institut Pertanian Bogor.
Enders, W. (2015). Applied Econometrics Time Series (4th ed.). USA: John Wiley & Sons.
Gujarati, D. N. (2004). Basic Econometrics (4th ed.). New York: McGraw-Hill.
Hadiyatullah. (2011). Model Vector Autoregressive (VAR) dan Penerapannya untuk Analisis Pengaruh Harga Migas terhadap Indeks Harga Konsumen (IHK). Jurnal Riset Pendidikan Matematika.
Heizer, J., Render, B., & Munson, C. (2011). Operations Management Sustainability and Supply Chain Management. Boston: Pearson.
Juanda, B., & Junaidi. (2012). Ekonometrika Deret Waktu Teori dan Aplikasi. Jakarta: Rajawali Press.
Lutkepohl, H. (2005). New Introduction to Multiple Time Series Analysis. Berlin: Springer.
Lutkepohl, H., & Kratzig, M. (2004). Applied Time Series Econometrics. New York: Cambridge University Press.
Nurullita, A. H. (2011, Desember). Pengujian Kausalitas Antara Variabel Makroekonomi dengan Return Pasar di Bursa Efek Indonesia: Sebuah Pendekatan
Vector Autoregression. Media Ekonomi, 19(3), 23-42.
Ramli, R. L., Sumarjaya, I., & Sari, K. (2019). Analisis Hubungan Produksi Perikanan Tangkap Laut, Curah Hujan, dan Suhu Permukaan Laut dengan Model Vector Autoregressive (VAR). E-Jurnal
Matematika, 8(2), 155-163.
Suarsana, M., Parmila, I. P., & Wahyuni, P. S. (2020, Juni). Pengaruh Serangan Hama Penggerek Batang dan Penyakit Tungro Terhadap Produktivitas Sembilan Varietas Padi di Lokapaksa Bali. Agricultural Journal, 3(1), 84-90.
Zhang, T., Wang, K., & Zhang, X. (2015). Modelling and Analyzing the Tranmission Dynamics of HBV Epidemic in Xianjiang, China. Plos One, 10(9), 110-121.
40
Discussion and feedback