RUTE TERPENDEK UNTUK PENGANGKUTAN SAMPAH DENGAN PENDEKATAN LINTASAN HAMILTON

E-Jurnal Matematika Vol. 10(2), Mei 2021, pp. 115-121

DOI: https://doi.org/10.24843/MTK.2021.v10.i02.p330

ISSN: 2303-1751

RUTE TERPENDEK UNTUK PENGANGKUTAN SAMPAH DENGAN PENDEKATAN LINTASAN HAMILTON

Syamsyida Rozi^1§, Cut Multahadah²

¹Program Studi Matematika, Fakultas Sains dan Teknologi, Universitas Jambi [syamsyida.rozi@gmail.com] ²Program Studi Matematika, Fakultas Sains dan Teknologi, Universitas Jambi [cutmultahadah@gmail.com]

^§Corresponding Author

ABSTRACT

This research is related to the route of picking up the waste which done by janitors in housing complex of Aur Duri Indah Rt.14 Jambi considering the condition of that housing which have some crossroads, such that janitors take the same road twice which seems inefficient in terms of time and fuel consumption. This research is aimed to identify scientifically about the shortest and more efficient route which should be taken by janitors. This problem is considered as optimization problem through graph modelling. To check the efficient route, the existence of Hamiltonian Path of the graph is identified by using Depth-First Search method, and so is the shortest path. It is found that there are 39 Hamiltonian paths and the shortest path has total distance of 793.8 meter. By the existence of the shortest Hamiltonian Path, it is confirmed that janitors in housing complex of Aur Duri Indah Rt.14 can travel each road once with total distance is about 793.8 meter.

Keywords: Depth-First Search, graph, Hamiltonian Path, route

• 1.    PENDAHULUAN

Kebersihan lingkungan merupakan salah satu aspek penting untuk kenyamanan hidup di suatu lingkungan dan menjadi salah satu indikator lingkungan yang sehat dan bebas dari serangan penyakit. Permasalahan yang sering muncul adalah tidak adanya kesadaran masyarakat untuk membuang sampah dengan tertib. Terkadang, sampah dibiarkan menumpuk terlebih dulu sehingga menimbulkan bau tak sedap, dan bahkan menjadi sumber tumbuh dan berkembangnya bakteri. Diantara faktor yang menyebabkan terjadi penumpukan sampah di sekitar rumah adalah kesibukan warga sehingga tidak sempat membuang sampah pada tempat penampungan sampah, terlebih lagi jika letak TPS (Tempat Pembuangan Sementara) yang jauh dari lingkungan perumahan. Oleh karena itu, keberadaan petugas kebersihan yang bisa membantu mengambil sampah dari setiap rumah pada suatu kompleks perumahan menjadi sangat penting. Salah satu perumahan di Kota Jambi yang punya fasilitas keberadaan petugas kebersihan yang bertugas mengambil sampah-sampah dari setiap rumah adalah Perumahan Aur Duri Indah Blok B RT. 14

Kec, Telanaipura, Kota Jambi.

Struktur Perumahan Aur Duri yang berblok-blok membuat petugas kebersihan menempuh rute perjalanan yang sering kali melalui suatu blok dua kali. Hal ini dirasa kurang efisien, baik dari segi waktu ataupun konsumsi bahan bakar. Rute terpendek atau rute optimal diharapkan mampu mempercepat selesainya pekerjaan petugas kebersihan dan menghemat pengeluaran akibat konsumsi bensin yang dikeluarkan oleh kendaraan pembawa sampah. Berdasarkan masalah tersebut peneliti tertarik membantu petugas kebersihan terkait menemukan rute terpendek atau terbaik untuk mengambil sampah dari rumah ke rumah di kompleks Perumahan Aur Duri Indah Blok B Rt.14, dan mengidentifikasi kemungkinan setiap ruas jalan bisa dilalui satu kali. Permasalahan ini merupakan salah satu masalah optimasi yang bisa ditemukan solusinya dengan pemodelan melalui graf.

Graf merupakan struktur diskrit yang mengandung verteks dan sisi yang menghubungkan verteks-verteks tersebut. Suatu graf G mengandung himpunan tak kosong V = { v₁, V₂ , ■■■} yang disebut dengan verteks/ titik/ node, dan himpunan lainnya E = { 1₁, 2₂ ,...} yang disebut dengan edges/

sisi. Graf dinotasikan dengan G = (V ,E}. Sisi pada graf biasanya dinotasikan dengan e — uv yang artinya sisi e menghubungkan verteks u dan v. Dalam hal ini dikatakan pula bahwa verteks u dan verteks v bertetangga, dan sisi e dikatakan bersisian dengan verteks u dan v. Diantara klasifikasi dari graf adalah adanya graf berbobot, yaitu graf yang sisinya diberi bobot, dan ada pula graf tidak berbobot, yaitu graf yang sisinya tidak diberi bobot. (Rosen, 2012)

Terminologi penting lainnya dalam graf adalah lintasan. Lintasan dari v₀ ke v_ merupakan barisan sisi-sisi e₀ ,e₁,...,e_n pada G dimana sisi-sisi tersebut menghubungkan verteks v₀,v₁, v₂, ., v__ ₁, v_ dalam G. Jika graf tersebut merupakan graf sederhana, lintasan biasanya dinotasikan dengan barisan verteks-verteksnya, yaitu v₀, v₁, v₂, ., v__ ₁, v_. Dua buah verteks pada graf dikatakan terhubung jika terdapat lintasan yang menghubungkan kedua verteks tersebut. (Rosen, 2012)

Suatu lintasan sederhana yang melalui setiap verteks dalam graf tepat satu kali disebut lintasan Hamilton. Pada lintasan Hamilton, verteks awal berbeda dengan verteks akhir. Namun jika verteks awal dan vertekas akhir lintasan sama, maka disebut dengan sirkuit Hamilton. Ada graf yang memiliki lintasan ataupun sirkuit Hamilton, dan ada pula graf yang tidak bisa memiliki lintasan ataupun sirkuit Hamilton. Graf yang memiliki sirkuit Hamilton disebut Graf Hamilton, dan graf yang memiliki lintasan Hamilton disebut Graf semi-Hamilton (Wilson, 1996). Pada Gambar 1, graf G₁ tidak memiliki lintasan Hamilton, sedangkan graf G₂ memiliki lintasan Hamilton yaitu beberapa diantaranya lintasan a — d — c — b, lintasan a — d — b — c dan lintasan b — c d — a _a

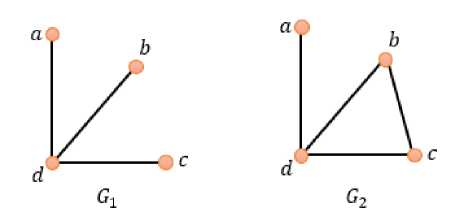
Gambar 1. Graf G₁ tidak mengandung lintasan Hamilton, dan graf G ₂ mengandung lintasan Hamilton

Jika G adalah suatu graf yang masing-masing verteksnya berderajat paling tidak/ minimal 2, maka G mengandung cycle, yaitu suatu graf yang setiap verteksnya berderajat 2. Dan cycle yang memiliki n buah verteks merupakan suatu graf Hamilton, atau memiliki lintasan Hamilton. (Vasudev, 2006)

Salah satu metode yang bisa digunakan untuk memverifikasi lintasan Hamilton adalah teknik Depth-First Search (DFS) (Riansanti et al., 2018). Pada dasarnya, DFS merupakan salah satu teknik untuk membangun spanning tree (Priskilla & Arulanandam, 2020), yaitu suatu subgraf tak berarah dari graf G yang dibentuk dengan cara membuang beberapa sisi pada graf G sedemikian sehingga subgrafnya terhubung, tidak memiliki sirkuit dan tetap mengandung setiap verktes dalam Gm Metode DFS juga merupakan suatu teknik traversal, yaitu teknik untuk mengunjungi verteks dalam suatu graf yang bisa digunakan untuk mengeksplor ataupun mengunjungi setiap verteks secara sistematis dalam graf (Rosen, 2012). Karena lintasan Hamilton merupakan suatu spanning tree (Vasudev, 2006), maka teknik DFS bisa digunakan untuk mengidentifikasi lintasan Hamilton. Sehingga implementasi dari teknik DFS pada suatu graf bisa menghasilkan lintasan Hamilton, bisa pula tidak.

Masalah alami yang dibahas dalam topik graf adalah pertanyaan-pertanyaan terkait lintasan terpendek antara satu verteks dengan verteks lainnya. Edsger Wybe Djikstra mempelopori algoritma tentang penemuan lintasan terpendek dari suatu verteks ke semua verteks lain dalam graf berbobot dengan bobot positif. Setelah itu banyak perkembangan terkait algoritma untuk menemukan lintasan terpendek pada graf. Beberapa algoritma dalam teori graf diantaranya Breadth-First Search (BFS), Depth-First Search (DFS), Bellman-Ford Algorithm, Floyd-Warshall Algorithm, Ford-Fulkerson Algorithm, etc. (Dondi et al., 2018). Teknik lain yang digunakan untuk menemukan lintasan terpendek, jika diinginkan lintasan tersebut melalui semua verteks dalam graf, adalah dengan pendekatan Graf Hamilton (Tamilarasi & Dhenakaran, 2018). Teknik tersebut juga diterapkan oleh Llopis et al., untuk menemukan lintasan terpendek, yaitu menemukan semua lintasan Hamilton dari graf, kemudian menghitung total cost untuk

masing-masing lintasan Hamilton (Llopis et al., 2014). Dan salah satu penerapan graf yang paling terkenal adalah Traveling Salesman Problem (TSP). Ada banyak metode yang telah diajukan oleh peneliti-peneliti sebelumnya terkait penemuan solusi dari masalah TSP yang sukses diaplikasikan untuk kasus-kasus tertentu. Diantaranya metode heuristik dengan teknik Tetangga Terdekat dan minimum spanning tree (Karkory & Abudalmola, 2013), algoritma Best-First Search (Abrori & Setiyani, 2015), dan sebagainya. Permasalahan dalam penelitian ini juga dikategorikan pada Travelling Salesman Problem.

• 2.    METODE PENELITIAN

Penelitian dilakukan di Perumahan Aur Duri Indah, Blok B, Rt.14, Kec. Telanai Pura, Kota Jambi, dengan visualisasi perumahan ditampilkan pada Gambar 2. Pengukuran jarak dilakukan dengan aplikasi Maps Ruler.

Ilustrasi ruas jalan yang harus dilalui oleh petugas kebersihan untuk mengambil/ mengangkut sampah, titik awal keberangkatan petugas dan lokasi akhir menaruh sampah di TPS (Tempat Pembuangan Sampah) adalah sebagaimana pada Gambar 3.

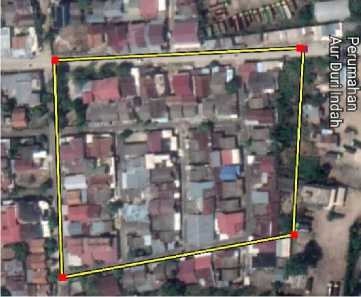
Sumber: Maps Ruler

Gambar 2.Visualisasi lokasi Perumahan Aur Duri Rt.14

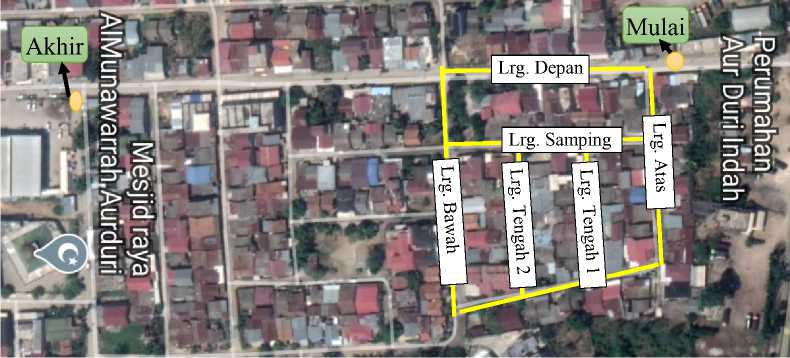
Gambar 3. Visualisasi Lokasi Perumahan Aur Duri Rt.14

Langkah-langkah penyelesaian masalah optimasi untuk menemukan rute terpendek pengambilan sampah di Perumahan Aur Duri Indah Blok B, Rt. 14 adalah:

• 1)    Memodelkan struktur perumahan ke dalam bentuk graf

• 2)    Mengidentifikasi dan menuliskan daftar lintasan Hamilton yang bisa dibentuk dari graf menggunakan teknik Depth-First Search (DFS). Pembentukan lintasan Hamilton ini bertujuan untuk mengidentifikasi kemungkinan rute perjalananan petugas kebersihan supaya setiap ruas jalan hanya dilalui sekali.

Prosedur teknik DFS untuk melakukan traversal dalam suatu graf adalah:

• a)    Pilih sembarang verteks dari verteks-verteks dalam graf untuk memulai traversal

• b)    Membentuk lintasan yang dimulai dari verteks tersebut dengan menambahkan verteks dan sisi berturut-turut, dimana setiap verteks baru yang dimasukkan ke dalam lintasan itu adalah tetangga dari verteks sebelumnya dan belum berada di dalam lintasan yang dibuat (setiap verteks muncul didalam lintasan tepat satu kali). Penambahan verteks dan sisi dapat dilakukan terus menerus ke dalam lintasan tersebut sepanjang itu memungkinkan.

• c)    Jika lintasan yang dibuat telah mengunjungi setiap verteks pada graf, maka traversal selesai.

• d)    Jika masih ada verteks yang belum dikunjungi, maka kembali ke verteks sebelumnya dalam lintasan dan jika mungkin, bentuk lintasan baru yang berawal dari verteks ini yang melalui verteks-verteks     yang     belum

dikunjungi. Proses kembali ke verteks sebelumnya ini disebut dengan backtrack, sehingga teknik DFS kadang disebut juga dengan teknik backtracking.

Namun jika lintasan masih belum bisa dibuat, maka kembali ke verteks lain di dalam lintasan, yaitu kembali ke dua verteks sebelumnya dalam lintasan dan coba lagi membuat lintasan baru.

• e)    Proses ini terus dilakukan dengan membentuk lintasan-lintasan baru sampai tidak ada lagi sisi yang bisa ditambahkan atau semua verteks telah dikunjungi.

(Rosen, 2012)

• 3) Mengidentifikasi lintasan Hamilton yang memiliki jarak terpendek.

• 3.    HASIL DAN PEMBAHASAN

Pada penelitian ini, untuk memodelkan permasalahan ke dalam bentuk graf, diasumsikan ruas jalan di kompleks tersebut sebagai verteks pada graf. Kemudian diasumsikan pula keterhubungan antara ruas jalan pada kompleks itu sebagai sisi pada graf. Graf yang dibentuk adalah graf berbobot, dimana setiap sisinya diberi bobot berdasarkan jarak antara ruas jalan (dengan satuan meter). Dengan demikian model grafnya adalah sebagaimana yang ditampilkan pada Gambar 4, dengan verteks A merepresentasikan tempat berangkat petugas dan verteks J tujuan TPS, sedangkan verteks B,C,D,E,F,G,H,I adalah ruas jalan yang harus dilalui petugas.

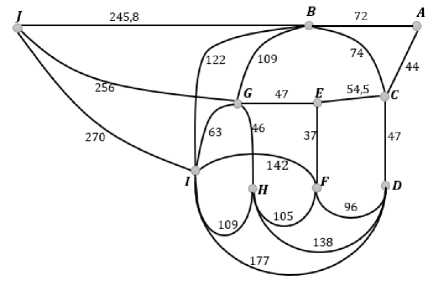
Gambar 4. Graf Rute Pengangkutan Sampah Di

Perumahan Aur Duri Rt. 14

Supaya semua sampah dari rumah-rumah dikawasan tersebut terangkut, maka dari model grafnya, akan ditemukan lintasan Hamilton dari verteks A ke verteks J . Graf Gambar 4 memiliki verteks-verteks berderajat minimal 2 sehingga graf tersebut memiliki cycle, dan pasti memiliki lintasan Hamilton. Untuk mengidentifikasi lintasan Hamilton pada graf Gambar 4, akan diimplementasikan teknik DFS. Proses pencarian akan dimulai dari verteks A (sebagai tempat keberangkatan petugas kebersihan) dan berakhir di verteks J (tujuan akhir tempat penitipan sampah). Proses teknik DFS yang dilakukan sebagai berikut:

• 1)    Menetapkan verteks A untuk memulai traversal dan menetapkan verteks J sebagai tujuan akhir.

• 2)    Dari verteks A , kemudian ditambahkan sisi yang menghubungkan A dengan B

• 3)    Dari verteks B, ditambahkan sisi yang menghubungkan B dengan I

• 4)    Dari verteks I, ditambahkan sisi yang menghubungkan I dengan H

• 5)    Dari verteks H, ditambahkan sisi yang menghubungkan H dengan F

• 6)    Dari verteks F, ditambahkan sisi yang menghubungkan F dengan D

• 7)    Dari verteks D , ditambahkan sisi yang menghubungkan D dengan C

• 8)    Dari verteks C, ditambahkan sisi yang menghubungkan C dengan E

• 9)    Dari verteks E, ditambahkan sisi yang menghubungkan E dengan G

• 10)    Dari verteks G , ditambahkan sisi yang menghubungkan G dengan J

Dengan demikian telah diperoleh sebuah lintasan Hamilton A-B-I-H-F-D-C-E-G-J , sebagaimana yang ditampilkan pada Gambar 5. Rute traversal ini diilustrasikan dengan garis berwarna merah.

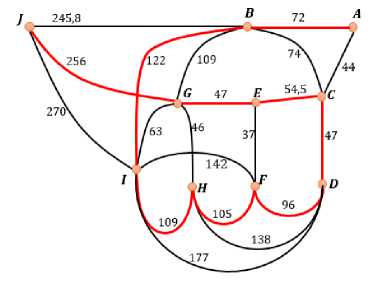
Gambar 5. Salah satu proses traversal (garis merah) pada graf dengan teknik DFS yang menghasilkan lintasan Hamilton.

Lintasan ini bukan satu-satunya lintasan Hamilton yang bisa dibentuk dari graf Gambar 4. Dengan prosedur teknis DFS yang sama, diperoleh 39 lintasan Hamilton yang berbeda untuk graf Gambar 4. Beberapa visualisasi lintasan Hamilton yang bisa dibentuk dari graf Gambar 4 ditampilkan pada Gambar 6. Dan total jarak untuk masing-masing lintasan Hamilton ditampilkan pada Tabel 1.

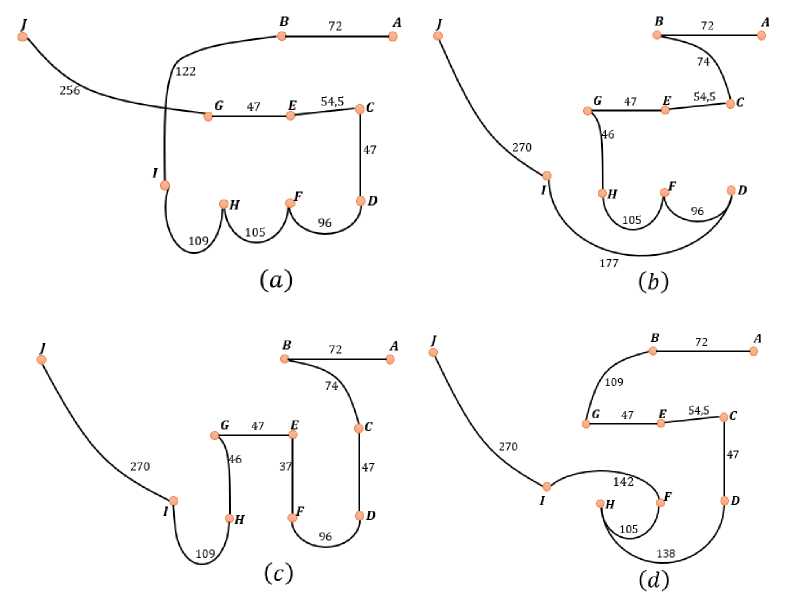
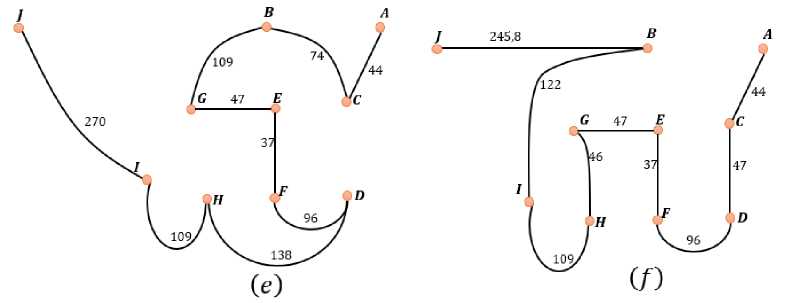
Gambar 6. Beberapa Lintasan Hamilton yang bisa dibuat dari graf Gambar 4

Tabel 1. Daftar semua lintasan Hamilton dari graf Gambar 7

No.		Lintasan Hamilton			Total jarak
1	A-B	-C-E-G	-H	-F-D-I-J	941,5
2	A-B	-C-E-G	-H	-D-F-I-J	939,5
3	A-B	-C-E-F	-H	-D-I-G-J	976,5
4	A-B	-C-E-F	-I-	-D-H-G-J	996,5
5	A-B	-C-E-F	-D	-H-I-G-J	899,5
6	A-B	-C-E-F	-D	-H-G-I-J	850,5
7	A-B	-C-E-F	-D	-I-H-G-J	921,5
8	A-B	-C-D-F	-E	-G-H-I-J	798
9	A-B	-C-D-H	-F	-E-G-I-J	853
10	A-B	-C-D-H	-I■	-F-E-G-J	922
11	A-B	-C-D-H	-G	-E-F-I-J	873
12	A-B	-C-D-I-	—H■	-F-E-G-J	924
13	A-B	-G-E-C	-D	-F-H-I-J	909,5
14	A-B	-G-E-C	-D	-H-F-I-J	984,5
15	A-B	-G-H-F	-E	-C-D-I-J	917,5
16	A-B	-G-H-D	-C	-E-F-I-J	915,5
17	A-B	-I-F-H■	-D ■	-C-E-G-J	983,5
18	A-B	-I-H-F■	-D ■	-C-E-G-J	908,5
19	A-B	-I-D-C-	—E-	—F-H-G-J	916,5
20	A-C	-B-G-E	-F	-D-H-I-J	924
21	A-C	-B-G-E	-F	-H-D-I-J	1001
22	A-C	-B-I-H■	-D ■	-F-E-G-J	923
23	A-C	-B-I-D-	-H■	-F-E-G-J	1000
24	A-C	-D-F-E	-G	-H-I-B-J	793,8
25	A-C	-D-H-F	-E	-G-B-I-J	919
26	A-C	-D-H-F	-E	-G-I-B-J	848,8
27	A-C	-D-H-I ■	-F-	—E-G-B-J	918,8
28	A-C	-D-H-G	-E	-F-I-B-J	868,8
29	A-C	-D-I-H ■	-F-	—E-G-B-J	920,8
30	A-C	-E-G-H	-F	-D-I-B-J	937,3
31	A-C	-E-G-H	-D	-F-I-B-J	935,5
32	A-C	-E-F-D	-H	-I-B-G-J	965,5
33	A-C	-E-F-D	-H	-I-G-B-J	896,3
34	A-C	-E-F-D	-H	-G-B-I-J	916,5
35	A-C	-E-F-D	-H	-G-I-B-J	846,3
36	A-C	-E-F-D	-I-	-H-G-B-J	918,3
37	A-C	-E-F-H	-D	-I-B-G-J	1042,5
38	A-C	-E-F-H	-D	-I-G-B-J	973,3
39	A-C	-E-F-I-	—D-	—H-G-B-J	993,3

Dengan demikian diperoleh lintasan Hamilton dengan bobot terpendek, yaitu dengan rute A-C-D-F-E-G-H-I-B-J dengan total jarak 793,8 meter. Visualisasi dari lintasan Hamilton terpendek ini ditampilkan pada Gambar 6 (f). Dari penemuan penelitian ini, dapat disarankan kepada petugas untuk mengambil dan mengangkut sampah dari rumah warga di Perumahan Aur Duri Indah Rt.

14 dengan menempuh ruas jalan: lorong atas – lorong tengah 1 – lorong samping - lorong tengah 2 - lorong bawah – lorong depan – TPS.

• 4.    KESIMPULAN DAN SARAN

Kesimpulan

Berdasarkan penelitian ini dan penyelesaian masalah optimasi melalui model graf, diperoleh kesimpulan bahwa terdapat efisiensi rute perjalanan petugas kebersihan untuk mengambil sampah dari rumah-rumah warga di Perumahan Aur Duri Indah, Blok B, Rt.14. Efisiensi itu berupa adanya rute terpendek yang bisa ditempuh oleh petugas kebersihan sedemikian sehingga setiap ruas jalan hanya dilalui satu kali saja, yaitu menempuh lorong atas – lorong tengah 1 – lorong samping -lorong tengah 2 - lorong bawah – lorong depan – TPS dengan total jarak 793,8 meter.

Saran

Pada penelitian berikutnya diharapkan dapat mengidentifikasi dan menginvestigasi secara ilmiah terkait rute terpendek pengangkutan sampah yang ditempuh oleh petugas kebersihan dengan kawasan yang lebih luas, misalnya, tingkat kecamatan atau tingkat kota. Dan hasil yang diperoleh pada penelitian, berupa rute terpendek dan yang lebih efisien, diharapkan mampu menjadi acuan bagi petugas kebersihan dalam melaksanakan tugasnya.

DAFTAR PUSTAKA

Abrori, M., & Setiyani, R. N. (2015).

Implementasi Algoritma Best-First Search (BeFS) pada Penyelesaian Traveling Salesman Problem (TSP) (Studi Kasus: Perjalanan Wisata Di Kota Yogyakarta). Jurnal Fourier, 4(2), 93.

https://doi.org/10.14421/fourier.2015.42.9 3-111

Dondi, R., Mauri, G., & Zoppis, I. (2018). Graph Algorithms. In Encyclopedia of Bioinformatics and Computational Biology: ABC of Bioinformatics. https://doi.org/10.1016/B978-0-12-809633-8.20424-X

Karkory, F. A., & Abudalmola, A. A. (2013). Implementation of Heuristics for Solving Travelling Salesman Problem Using Nearest Neighbour and Minimum Spanning Tree Algorithms. 7(10), 987– 997.

Llopis, C., Llopis, S., & Llopis, J. D. (2014). Resolving Hamiltonian Path Problems, Travelling Salesman Problems, Euclidean Problems and Route Problems with Inchrosil. 5(8), 669–676.

Priskilla, D. J., & Arulanandam, K. (2020). An Node Search of DFS with Spanning Tree in Undirected Graphs. 3, 2465–2470.

https://doi.org/10.35940/ijitee.B7887.0193 20

Riansanti, O., Ihsan, M., & Suhaimi, D. (2018). Connectivity algorithm with depth first search (DFS) on simple graphs.

Journal of Physics: Conference Series, 948(1). https://doi.org/10.1088/1742-6596/948/1/012065

Rosen, K. H. (2012). Discrete Mathematics and Its Aplications (7th ed.). McGraw-Hill.

Tamilarasi, M., & Dhenakaran, S. S. (2018). Hamiltonian Approach for Finding Shortest Path. 4(8), 484–488.

Vasudev, C. (2006). Graph Theory with Applications. New Age International (P) Limited.

Wilson, R. J. (1996). Introduction to Graph Theory (4th ed.). Longman.

121