PERAMALAN NILAI TUKAR PETANI MENGGUNAKAN METODE SINGULAR SPECTRUM ANALYSIS
on
E-Jurnal Matematika Vol. 9(3), Agustus 2020, pp. 171-176
DOI: https://doi.org/10.24843/MTK.2020.v09.i03.p295
ISSN: 2303-1751
PERAMALAN NILAI TUKAR PETANI MENGGUNAKAN METODE SINGULAR SPECTRUM ANALYSIS
Gilang Bimasakti Andhika1§, I Wayan Sumarjaya2, I Gusti Ayu Made Srinadi3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: gilang.1316@gmail.com]
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id]
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: srinadi@unud.ac.id]
§Corresponding Author
ABSTRACT
Singular spectrum analysis (SSA) is a new method in time series analysis that uses a nonparametric approach. The purpose of this study is to determine the model and forecast the farmer exchange rate in the Province of Bali using SSA. Vector singular spectrum analysis (VSSA) forecasting method is used to calculate the accuracy of forecasting. The best SSA model is obtained with a window length (L) value of 57 and produces a MAPE value of 0.49%. In conclusion, SSA method can predict farmer exchange rate in the Province of Bali very accurate.
Keywords: farmer exchange rate, singular spectrum analysis, VSSA
Indonesia dikenal sebagai negara agraris yang sebagian besar penduduknya bekerja pada sektor pertanian. Kebutuhan pangan yang diperoleh dari sektor pertanian sangatlah penting bagi kelangsungan hidup penduduk, sehingga kesejahteraan para petani perlu diperhatikan.
Nilai tukar petani (NTP) adalah salah satu indikator untuk mengukur tingkat kesejahteraan petani. NTP merupakan perbandingan antara indeks harga yang diterima petani (If ) dan indeks harga yang dibayar petani ( h)) (BPS Bali, 2018). Dalam mengukur kesejahteraan petani, diharapkan It meningkat sedangkan ^b menurun. Sehingga peramalan diperlukan untuk mengetahui potensi sektor pertanian ke depannya.
Terdapat banyak metode untuk meramal yang telah berkembang dalam metode deret waktu, salah satunya adalah metode singular spectrum analysis (SSA). SSA adalah metode baru dalam analisis deret waktu yang menggabungkan elemen analisis deret waktu klasik, statistika multivariat, geometri multivariat, sistem dinamik, dan pemrosesan sinyal. Tujuan SSA adalah mendekomposisi data asli menjadi sejumlah kecil komponen independen sehingga dapat lebih mudah untuk diinterpretasi (Hassani, 2007).
Penelitian terdahulu tentang SSA telah dilakukan antara lain oleh peneliti-peneliti berikut. Sakinah (2018) meneliti akurasi peramalan long horizon dengan recurrent SSA (RSSA) dan vector SSA (VSSA) yang menghasilkan mean absolute percentage error (MAPE) secara berturut-turut 5,0029 dan 4,0067. Sari dkk. (2019) meramalkan jumlah kunjungan wisatawan mancanegara ke Bali dan menghasilkan model SSA terbaik dengan window length (L) 94 dan MAPE sebesar 7,65%.
Pada penelitian ini penulis menggunakan metode SSA untuk memodelkan dan mengetahui hasil peramalan NTP di Provinsi Bali.
Jenis data yang digunakan adalah data sekunder yang diperoleh dari Badan Pusat Statistik Provinsi Bali. Data yang digunakan adalah data bulanan dari periode Januari 2008 hingga Desember 2019 yang dibagi menjadi dua yaitu data in-sample sebanyak 132 data yaitu periode Januari 2008 hingga Desember 2018 dan data out-sample sebanyak 12 data yaitu periode Januari 2019 hingga Desember 2019.
Langkah-langkah yang digunakan untuk menganalisis dengan bantuan program R 3.6.2 adalah sebagai berikut:
-
1. Mempersiapkan data in-sample nilai tukar petani di Provinsi Bali.
-
2. Menyusun data menjadi bentuk data deret waktu.
-
3. Melakukan plot data untuk mengetahui pola data.
-
4. Tahap dekomposisi. Tahap ini dibagi menjadi dua langkah yaitu:
-
a. Embedding
Pada langkah ini, dibentuk matriks lintasan X berukuran L×K dari data deret waktu. Pemilihan Window length (L) dilakukan secara coba-coba (trial and N error) yang memenuhi 2≤L ≤ dengan N=132 danK= -L+1.
-
b. Singular value decomposition (SVD)
Langkah ini mendekomposisi matriks lintasan X sebanyak d matriks dengan d = max{i, ^i>0}. Masing-masing
matriks hasil dekomposisi ( ^l ,…,Xc]) dapat dinyatakan sebagai ^i =√Wl . Kumpulan (√λι, Ui , Vf) merupakan
eigentriple matriks X^.
-
5. Tahap rekonstruksi. Tahap ini dibagi menjadi dua langkah yaitu:
-
a. Grouping
Pada langkah ini, dikelompokkan matriks hasil dekomposisi yang telah dipartisi, kemudian menjumlahkan setiap
kelompok matriks yang dinyatakan X= +⋯+X/ . Selanjutnya menge
lompokkan komponen tren, musiman, dan noise menggunakan plot nilai singular. Dari plot nilai singular diperoleh r yang digunakan untuk membatasi jumlah eigentriple. Eigentriple digunakan untuk mengidentifikasi komponen tren dan musiman. Komponen tren dapat dilihat dari eigentriple yang bervariasi lambat, sedangkan komponen musiman dilihat berdasarkan kemiripan dari dua eigentriple yang berurutan. Melakukan ESPRIT pada setiap dua eigentriple berurutan yang terpilih. Dari hasil ESPRIT dipilih pasangan eigentriple yang memiliki periode musiman sebesar 12, 6, 4, 3, 2 untuk dikelompokkan ke dalam komponen musiman.
-
b. Diagonal Averaging
Pada langkah akhir ini, dibentuk deret baru dengan panjang N menjadi deret yang sesuai terhadap masing-masing hasil grouping komponen tren dan musiman.
-
6. Membentuk model SSA dengan mencari
koefisien tren dan koefisien musiman dari
hasil diagonal averaging menggunakan
̃i, i=1,…,K.
θ(v)Zl-ι, i= +1,…,K+ℎ+L-1.
-
7. Melakukan peramalan menggunakan
VSSA.
-
8. Menghitung tingkat error peramalan
menggunakan MAPE.
-
9. Menginterpretasi hasil peramalan dan
menarik kesimpulan.
Bagian ini membahas penerapan metode SSA untuk meramalkan NTP di Provinsi Bali. Berikut hasil plot data NTP di Provinsi Bali.
Nilai Tukar Petani Provinsi Bali

2008 2010 2012 2014 2016 2018
Tahun
Gambar 1. Plot Data Nilai Tukar Petani di Provinsi Bali periode Januari 2008 hingga Desember 2019
Gambar 1 memperlihatkan bahwa pada tiga tahun awal terdapat pola tren naik. Pada tahun selanjutnya terlihat pola tren cenderung menurun, hal ini disebabkan harga konsumsi dan biaya produksi lebih besar dibandingkan dengan harga produksi. Selain itu, terdapat pola berulang yang mengindikasi adanya pola musiman pada data.
Langkah awal dalam tahap dekomposisi adalah embedding. Pertama dilakukan pemilihan nilai window length (L) secara coba-coba (trial and error). Pada penelitian ini banyak data yang digunakan sebanyak 132
data. Oleh karena itu nilai L yang memenuhi adalah 2 < L < 66. Dilakukan coba-coba nilai L = 55,56,57,58,59 kemudian diperoleh nilai MAPE berturut-turut 0,501%, 0,502%, 0,49%, 0,504%, 0,51%.
Nilai L yang dipilih setelah dilakukan proses coba-coba yaitu L = 57 dan X = 76. Pemilihan nilai L didasarkan pada nilai MAPE minimum yaitu sebesar 0,49%. Dengan demikian, matriks lintasan X dapat disusun sebagai berikut:
eigentriple 50 diidentifikasi sebagai komponen noise, sehingga nilai r adalah 16. Dengan demikian, banyak eigentriple yang akan digunakan untuk mengidentifikasi komponen tren dan musiman adalah enam belas eigentriple. Dari enam belas eigentriple terdapat kemungkinan ada eigentriple yang mencerminkan komponen noise, hal ini dapat diketahui dari sisa eigentriple yang tidak mencerminkan komponen tren dan musiman.
X = [X1:
(
101,63
101,57
108,46
:X76] = (¾) 101,57 -
99,24 -
108,93
5 7,76 _ i ,7=1 =
103,8
104,4
103,87.
)
Langkah selanjutnya yaitu SVD dengan mendekomposisi matriks lintasan X menjadi 50 eigentriple yang terdiri dari 50 nilai eigen dan 50 vektor eigen.
3.2.2 Pengelompokan Komponen Tren dan Musiman
Eigentriple yang akan digunakan untuk mengidentifikasi komponen tren dan musiman adalah sebanyak enam belas eigentriple. Enam belas eigentriple yang digunakan untuk mengidentifikasi komponen tren dan musiman terdiri dari eigentriple 1,2,3, ...,16. Dalam mengidentifikasi eigentriple yang berhubungan dengan tren dan musiman dapat menggunakan plot deret yang direkonstruksi.
3.2 Rekonstruksi
Terdapat dua langkah dalam tahap rekonstruksi yaitu grouping dan diagonal averaging.
3.2.1 Pengelompokan Komponen Noise
Langkah awal dalam tahap rekonstruksi adalah mengelompokkan eigentriple menjadi komponen tren, musiman, dan noise. Grouping effects (r) merupakan parameter dalam langkah grouping yang berguna untuk membatasi jumlah eigentriple yang akan digunakan saat mengidentifikasi komponen tren dan musiman. Nilai r ditentukan berdasarkan jumlah eigentriple yang tidak mencerminkan noise pada plot nilai singular.

Gambar 3. Plot Deret yang Direkonstruksi

Gambar 2. Plot Nilai Singular
Gambar 2 menunjukkan plot nilai singular dari 50 eigentriple. Terlihat nilai singular mulai menurun secara lambat dari eigentriple 17. Hal ini menyebabkan eigentriple 17 hingga
Gambar 3 memperlihatkan bahwa deret yang direkonstruksi oleh eigentriple 1 dan eigentriple 2 memuat komponen yang bervariasi lambat. Oleh karena itu, eigentriple 1 dan eigentriple 2 dikelompokkan ke dalam komponen tren. Selanjutnya dilakukan pengelompokan eigentriple ke dalam komponen musiman yang dilakukan berdasarkan kemiripan eigentriple yang berurutan. Pada plot deret yang direkonstruksi, kemiripan eigentriple mengakibatkan deret yang direkonstruksi memiliki pola dan periode musiman yang sama.
Pada Gambar 3 terlihat beberapa pasang eigentriple berurutan yang memiliki kemiripan pola yaitu eigentriple 5 dan 6, eigentriple 7 dan 8, eigentriple 10 dan 11, serta eigentriple
15 dan 16. Dengan ESPRIT diperoleh deret yang direkonstruksi eigentriple 15 dan 16 memiliki periode musiman yang sama yakni empat sehingga dikelompokkan ke dalam komponen musiman. Selanjutnya, deret yang direkonstruksi eigentriple 5 dan 6 memiliki periode musiman yang sama yakni tiga belas. Meskipun deret yang direkonstruksi oleh eigentriple 5 dan 6 memiliki periode musiman yang sama, tetapi kedua eigentriple tersebut tidak dapat dikelompokkan ke dalam komponen musiman. Hal ini dikarenakan periode musiman kedua deret tersebut tidak dapat diinterpretasikan untuk data bulanan.
W-correlation matrix

Gambar 4. Plot Keterpisahan (W-correlation)
Selain melihat plot deret yang direkonstruksi, proses identifikasi eigentriple yang mencerminkan komponen tren dan musiman dapat dilihat pada plot keterpisahan (w-correlation). Plot keterpisahan (w-correlation) ini digunakan untuk melihat besarnya korelasi antar eigentriple. Semakin tua warnanya maka semakin tinggi korelasinya. Plot keterpisahan (w-correlation) dari enam belas eigentriple ditunjukkan pada Gambar 4.
Gambar 4 memperlihatkan pasangan eigentriple 5 dan 6, eigentriple 7 dan 8, eigentriple 10 dan 11, serta eigentriple 15 dan 16 memiliki korelasi yang kuat. Akan tetapi, untuk mengidentifikasi komponen musiman tidak dapat ditentukan hanya dengan melihat plot. Sehingga digunakan ESPRIT untuk mencari periode musiman dari deret yang direkonstruksi dari dua eigentriple. Tabel 1 menyajikan secara lengkap pasangan eigentriple beserta periode musimannya.
Tabel 1 Eigentriple dan Periode Musiman
|
Eigentriple |
Periode |
Eigentriple |
Periode |
|
5 |
13 |
10 |
47 |
|
6 |
13 |
11 |
47 |
|
7 |
21 |
15 |
4 |
|
8 |
21 |
16 |
4 |
Sumber: Data diolah, 2020
Pasangan eigentriple yang memiliki periode musiman yang sama dapat diinterpretasikan untuk data bulanan berdasarkan Tabel 1 adalah eigentriple 15, dan 16. Sehingga, eigentriple 15, dan 16 dapat dikelompokkan ke dalam kelompok komponen musiman.
Eigentriple yang dikelompokkan ke dalam kelompok komponen tren adalah eigentriple 1 dan 2. Selanjutnya eigentriple yang dikelompokkan ke dalam kelompok komponen musiman adalah eigentriple 15, dan 16. Terakhir, eigentriple yang tidak dikelompokkan ke dalam kelompok komponen tren dan musiman merupakan kelompok komponen noise.
3.2.3 Diagonal Averaging
Langkah selanjutnya yaitu diagonal averaging. Masing-masing komponen direkonstruksi menggunakan eigentriple yang terkait. Pada penelitian ini, komponen tren direkonstruksi oleh eigentriple 1 dan 2. Plot hasil dari komponen tren yang direkonstruksi adalah sebagai berikut.

Gambar 5. Komponen Tren yang Direkonstruksi
Selanjutnya komponen musiman direkonstruksi oleh eigentriple 15, dan 16. Plot hasil dari komponen musiman yang direkonstruksi dapat dilihat pada Gambar 6.
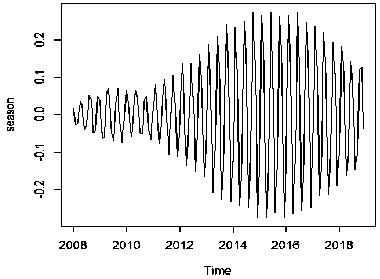
Gambar 6. Komponen Musiman yang Direkonstruksi
Sedangkan plot hasil dari komponen noise yang direkonstuksi dapat dilihat pada Gambar 7.

Gambar 7. Komponen Noise yang Direkonstruksi
3.3 Peramalan
Saat seluruh komponen berhasil dipisahkan, maka langkah selanjutnya adalah melakukan peramalan terhadap komponen tren dan musiman. Metode yang digunakan untuk meramalkan komponen tren dan musiman adalah vector singular spectrum analysis (VSSA). Data in-sample sebanyak N = 132, sehingga peramalan dengan data out-sample pada selang ℎ=12 yakni ̃133,…, ̃144 diperoleh rumus vector sebagai berikut:
Xi, i=1,…,76.
θ(v)Zi-i,i=77,…,144.
Z1 ={
dengan Z^,…, ^144 merupakan nilai-nilai dari deret rekonstruksi dan θ(V) merupakan
koefisien dari VSSA.
Model SSA untuk meramalkan komponen tren dapat ditulis sebagai berikut:
zl = 101,69zl + 101,75zl +⋯+104,2Zf^ .
Selanjutnya, model SSA untuk meramalkan komponen musiman dapat ditulis sebagai berikut:
zl = 0,024zl - 0,022zl+⋯-0,1Zβ3 .
Nilai ramalan data out-sample secara keseluruhan diperoleh dari penjumlahan nilai ramalan data out-sample dari komponen tren dan komponen musiman. Secara matematis, model SSA untuk memperoleh nilai ramalan data out-sample secara keseluruhan dapat ditulis sebagai berikut:
Zi = + zf , untuk i=132,…,144.
Setelah diperoleh model SSA yang digunakan untuk melakukan peramalan, maka langkah selanjutnya melakukan peramalan pada data out-sample berdasarkan model yang diperoleh. Akurasi hasil peramalan pada data out-sample diukur dengan nilai MAPE yang merupakan nilai rata-rata persentase kesalahan dari beberapa periode. Tabel 2 menyajikan hasil peramalan data out-sample dari komponen tren dan musiman untuk dua belas bulan ke depan.
Tabel 2. Hasil Peramalan Data Out-Sample dari Komponen Tren dan Musiman
|
Bulan |
Hasil Ramalan |
Data Aktual |
Persentase Kesalahan |
|
Januari |
104,13 |
103,65 |
0,00458 |
|
Februari |
104,18 |
103,98 |
0,00190 |
|
Maret |
104,25 |
104,10 |
0,00143 |
|
April |
104,14 |
103,40 |
0,00711 |
|
Mei |
103,99 |
103,30 |
0,00667 |
|
Juni |
104,02 |
103,50 |
0,00499 |
|
Juli |
104,09 |
104,80 |
0,00679 |
|
Agustus |
103,99 |
104,65 |
0,00625 |
|
September |
103,85 |
104,14 |
0,00281 |
|
Oktober |
103,85 |
103,66 |
0,00183 |
|
November |
103,92 |
104,35 |
0,00413 |
|
Desember |
103,85 |
104,93 |
0,01033 |
|
Total Persentase Kesalahan |
0,05885 | ||
|
MAPE |
0,00490 | ||
Sumber: Data diolah, 2020
Menurut Zhang dkk. (2015) nilai MAPE yang kurang dari 10% menunjukkan bahwa peramalan sangat akurat. Berdasarkan Tabel 2, diperoleh nilai MAPE pada data out-sample sebesar 0,0049 atau 0,49%. Dengan demikian, dapat disimpulkan bahwa metode SSA dengan L=57 dapat meramalkan nilai tukar petani di Provinsi Bali dengan sangat akurat.
4. SIMPULAN DAN SARAN
Berdasarkan hasil dan pembahasan, diperoleh model SSA yang digunakan untuk meramalkan komponen tren dua belas bulan ke depan yaitu sebagai berikut:
Zf = 101,69zl + 101,75zl+⋯+104,2Zβ3 .
Kemudian model SSA yang digunakan untuk meramalkan komponen musiman dua belas bulan ke depan dapat ditulis sebagai berikut:
zi = 0,024Zf - 0,022Zf+⋯-0,1Z63 .
Model tersebut merupakan model SSA terbaik dengan nilai window length L=57 serta nilai MAPE sebesar 0,49%. Hal ini menunjukkan bahwa metode SSA dapat meramalkan nilai tukar petani di Provinsi Bali dengan sangat akurat.
Saran untuk penelitian selanjutnya yaitu pada proses pengelompokan komponen tren dan musiman dapat menambahkan atau menggunakan cara lain seperti analisis periodogram dan pairwise scatterplot.
DAFTAR PUSTAKA
Badan Pusat Statistik Provinsi Bali. 2018.
Indeks Nilai Tukar Petani Provinsi Bali 2018. Badan Pusat Statistik Provinsi Bali. Denpasar: BPS Provinsi Bali.
Hassani, Hossein. 2007. “Singular Spectrum Analysis: Methodology and
Comparison.” Journal of Data Science 5:
239–257.
Sakinah, Awit Marwati. 2018. “Akurasi
Peramalan Long Horizon Dengan
Singular Spectrum Analysis.” Kubik 3(2): 93–99.
Sari, Mira Ayu Novita, I Wayan Sumarjaya, and Made Susilawati. 2019. “Peramalan Jumlah Kunjungan Wusatawan
Mancanegara Ke Bali Menggunakan Metode Singular Spectrum Analysis.” E-Jurnal Matematika 8(4): 303–308.
Zhang, Tailei, Kai Wang, and Xueliang Zhang. 2015. “Modeling and Analyzing the Transmission Dynamics of HBV Epidemic in Xinjiang, China.” PLoS ONE 10(9): 1–14.
176
Discussion and feedback