DIMENSI METRIK GRAPH LOBSTER Ln (q;r)

E-Jurnal Matematika Vol. 2, No.2, Mei 2013, 42-48

ISSN: 2303-1751

DIMENSI METRIK GRAPH LOBSTER L_n (q; r)

Pande Gde Dony Gumilar¹, Luh Putu Ida Harini²,

Kartika Sari³

• ^1,2,3Jurusan Matematika FMIPA Universitas Udayana, Bukit Jimbaran-Bali e-mail: ¹ pande.dony@gmail.com , ² ballidah@gmail.com, ³sari_kaartika@yahoo.co.id

Abstract

The metric dimension of connected graph G is the cardinality of minimum resolving set in graph G. In this research, we study how to find the metric dimension of lobster graph L_n (q; r). Lobster graph L_n (q; r) is a regular lobster graph with n vertices backbone on the main path, every backbone vertex is connected to q hand vertices and every hand vertex is connected to r finger vertices, with n, q, r ∈ N, n ≥ 2. We obtain the metric dimension of lobster graph L₂(1; 1) is 1, the metric dimension of lobster graph L_n (1; 1) for n >2 is 2, the metric dimension of lobster graph L_n (q; 1) for n≥ 2 and q ≥ 2 is n(q — 1) and the metric dimension of lobster graph L_n (q; r) for n≥ 2, q ≥ 1 and r ≥ 2 is nq(r — 1).

Keywords: lobster graph, metric dimension, resolving set.

• 1.    Pendahuluan

Graph adalah pemodelan matematika dalam bentuk geometri yang diwakili oleh diagram vertex dan edge sedangkan teori graph merupakan pemikiran matematis yang mengkaji sifat dan struktur graph. Beberapa penelitian yang menggunakan konsep graph yaitu navigasi robot [5], permasalahan berat koin [6], penemuan jaringan dan verifikasi [1], dan mastermind of the game [2]. Konsep graph yang digunakan pada penelitian-penelitian tersebut adalah dimensi metrik dari suatu graph terhubung.

Diberikan suatu graph terhubung G, misalkan u dan v adalah vertex-vertex dalam graph terhubung G, panjang lintasan terpendek dari u ke v pada G dinotasikan d(u,v). Jika W = {w₁,w₂,w₃,... ,w_k} suatu himpunan terurut dari vertex - vertex dalam graph terhubung G dan vertex v di V (G) maka representasi jarak dari vertex v terhadap W adalah

r(v∣W) = (d(v,W1 ),d(v,w2), ■■■ ,d(v,w_k)).

Jika r(v∣W) untuk setiap vertex v ∈V(G} berbeda, maka W disebut himpunan pemisah dari G. Himpunan pemisah dengan kardinalitas (banyak anggota) minimum disebut himpunan pemisah minimum atau basis metrik. Kardinalitas dari basis metrik tersebut dinamakan dimensi metrik dari G, yang

• ¹    Mahasiswa Jurusan Matematika FMIPA Universitas Udayana

• ^2,3 Staf Pengajar Jurusan Matematika FMIPA Universitas Udayana

dinotasikan dim(G) [3]. Dengan demikian, dimensi metrik pada graph G adalah kardinalitas minimum himpunan pemisah dari G.

Terdapat banyak jenis graph. Salah satu jenis graph yang jarang dibahas adalah graph lobster. Graph lobster adalah graph pohon yang setiap vertexnya memiliki jarak paling banyak t dari lintasan utama, dengan t adalah suatu bilangan bulat positif [4]. Pada penelitian ini ditentukan dimensi metrik graph lobster teratur dengan t = 2.

• 1.1    Graph Lobster

Graph lobster L_n (q; r) merupakan graph lobster teratur yang memiliki n vertex backbone pada lintasan utama, setiap vertex backbone dihubungkan dengan q vertex hand dan setiap vertex hand dihubungkan dengan r vertex finger, dengan n, q, r ∈N, n≥ 2. Contohnya, diberikan suatu graph lobster L_n (q; r) dengan n = 3, q = 2 dan r = 4 yang ditunjukkan pada Gambar 1.

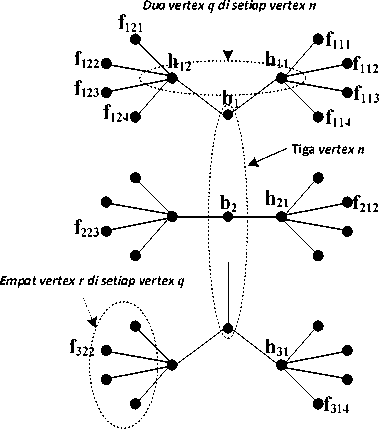
Gambar 1. Pelabelan graph lobster L_n (q; r)

Keterangan

b: Label vertex lintasan utama

h: Label vertex berjarak 1 dari lintasan utama

f : Label vertex berjarak 2 dari lintasan utama

Dalam tulisan ini pelabelan vertex-vertex dalam graph lobster dijelaskan sebagai berikut. Vertex b_i merupakan vertex backbone ke-i. Vertex h_ij merupakan vertex hand ke-j yang terhubung dengan vertex b_i. Vertex fa merupakan vertex finger ke-k yang terhubung dengan vertex b_i dan vertex hand ke-j.

• 2.    Metode Penelitian

Langkah awal dalam penelitian ini adalah mempelajari teori graph, graph lobster dan dimensi metrik. Langkah selanjutnya yang dilakukan adalah eksplorasi bentuk-bentuk dari graph lobster L_n (q; r) dengan cara menentukan himpunan pemisahnya dengan memasukkan nilai n, q dan r tertentu. Lebih lanjut lagi, berdasarkan hasil eksplorasi akan dilakukan studi kasus dimensi metrik graph lobster L_n(q; r). Kemudian ditarik kesimpulan dari hasil analisis tersebut.

• 3.    Hasil dan Pembahasan

Terlebih dahulu untuk memudahkan menentukan dimensi metrik tersebut diberikan lemma berikut.

Lemma 3.1 Diberikan graph terhubung G dan    v_i EV(G) dengan

i = 1,2,3,... ,'n. Graph G berdimensi metrik satu jika dan hanya jika graph G merupakan graph lintasan.

Lemma 3.2 Diberikan graph G dan himpunan vertx-vertex W dengan W ⊆ V(G). Jika w E W maka w memiliki representasi jarak yang berbeda terhadap W.

• 3.1    Dimensi Metrik Graph Lobster L₂ (1; 1)

Gambar 3.1 merupakan gambar graph lobster L₂ (1; 1). b1             h11

f111

_b2              21              _f211

Gambar 2. Graph lobster L₂(1; 1)

Perhatikan Gambar 2. Tampak bahwa graph lobster tersebut merupakan graph lintasan. Berdasarkan Lemma 3.1 diperoleh dimensi metrik graph lobster L₂ (1; 1) adalah satu. Berdasarkan hasil ini diperoleh teorema berikut.

Teorema 3.3 Diberikan graph lobster L_n (q; r). Jika n = 2, q = 1 dan r = 1 maka dim{L_n(q; r)) = 1.

• 3.2    Dimensi Metrik Graph Lobster L_n (1; 1) untuk n >2

Berikut ini diberikan lemma yang menyangkut himpunan pemisah pada graph lobster L_n(1; 1) untuk n >2.

Lemma 3.4 Diberikan graph lobster L_n (q; r). Jika n >2, q = 1 dan r = 1 maka vertex backbone ke-1 dan vertex finger ke-n merupakan himpunan pemisah.

Bukti :

Diambil himpunan W = {b₁, f_n11} pada graph lobster L_n (1; 1) diperoleh bahwa setiap vertex yang bukan himpunan W memiliki representasi jarak yang berbeda terhadap W, sedangkan berdasarkan Lemma 3.2 setiap vertex pada himpunan W memiliki representasi jarak yang berbeda terhadap W, sehingga himpunan W merupakan himpunan pemisah.

Berdasarkan Lemma 3.4 diperoleh teorema yang menyangkut dimensi metrik pada graph lobster L_n(1; 1) untuk n >2.

Teorema 3.5 Diberikan graph lobster L_n (q; r). Jika n >2, q = 1 dan r = 1 maka dim(L_n(q; rf) = 2.

Bukti :

Berdasarkan Lemma 3.1 dan Lemma 3.4 diperoleh dim(L_n(1;1)) = 2 untuk n >2.

• 3.3    Dimensi Metrik Graph Lobster L_n(q; 1) untuk n ≥ 2 dan q ≥ 2

Berikut ini diberikan lemma-lemma yang menyangkut himpunan pemisah pada graph lobster L_n(q; 1) untuk n ≥ 2 dan q ≥ 2.

Lemma 3.5 Diberikan graph lobster L_n (q; r). Jika n≥ 2, q≥ 2 dan r = 1 maka gabungan sedikitnya (q — 1) vertex finger di setiap vertex backbone merupakan himpunan pemisah.

Bukti :

Tanpa mengurangi keumuman bukti, diambil himpunan W = {f₁₁₁, f₁₂₁, f₁₃₁, —, ^f1(q—1)1^{, f}211^{, f}221^{, f}231^, — ^{, f}2(q—1)1^, ■■■^{, f}n1q^{, f}n21^{, f}n31^, — ^{, f}n(q—1)1} ^{pada graph} lobster L_n (q;1), diperoleh setiap vertex yang bukan himpunan W memiliki representasi jarak yang berbeda terhadap W, sedangkan berdasarkan Lemma 3.2 setiap vertex pada himpunan W memiliki representasi jarak yang berbeda terhadap W. Dengan demikian W merupakan himpunan pemisah. Lebih lanjut lagi, misalkan himpunan W digabungkan dengan himpunan Y yang anggota-anggotanya merupakan vertex-vertex yang bukan di W, notasikan dengan W', maka W =WuY. Berdasarkan Lemma 3.2, setiap anggota W' mempunyai representasi jarak yang berbeda terhadap W'. Di lain pihak, berdasarkan hasil terdahulu, bahwa setiap vertex pada graph lobster L_n (q; 1) dengan n≥ 2 dan q ≥ 2 yang bukan anggota W memiliki representasi jarak yang berbeda terhadap W, maka setiap vertex pada graph lobster tersebut yang bukan anggota W' memiliki representasi jarak yang berbeda terhadap W'. Oleh karena itu, W' merupakan himpunan pemisah. Jadi gabungan sedikitnya (q — 1) vertex finger di setiap vertex backbone merupakan himpunan pemisah.

Lemma 3.6 Diberikan graph lobster L_n (q; r). Jika n≥ 2, q≥ 2 dan r = 1 maka gabungan (q — 1) vertex finger di setiap vertex backbone adalah himpunan bagian dari himpunan pemisah minimum (f) dari graph lobster tersebut.

Bukti :

Tanpa mengurangi keumuman bukti, diambil gabungan (q — 1) vertex finger di setiap vertex backbone yaitu W = {fm,f121,f131, —,f1(q-1)1,f211,f221,f231 , —, f2(q-1)1, —, fn11, fn21, fn31, —, fn(q-1)1} diperoleh kardinalitas himpunan W adalah n(q — 1). Berdasarkan Lemma 3.5, W merupakan himpunan pemisah. Akan ditunjukkan bahwa W ⊆ f. Andaikan W bukan himpunan bagian dari β.

Dengan kata lain, terdapat vertex finger yang merupakan anggota di W tetapi bukan merupakan anggota di β. Tanpa mengurangi keumuman bukti, misalkan vertex tersebut vertex finger f₁₁₁ atau f₁₁₁ ∉ β. Diperoleh bahwa terdapat vertex yang memiliki representasi jarak yang sama, yaitu

r(fm W = r(f1q1∣β)

Hal ini berarti β bukan merupakan himpunan pemisah minimum. Terjadi kontradiksi, oleh karena itu f₁₁₁ ∈ β. Jadi W ⊆ β.

Berdasarkan Lemma 3.5 dan Lemma 3.6 diperoleh teorema yang menyangkut dimensi metrik pada graph lobster L_n(q; 1) untuk n≥ 2 dan q ≥ 2.

Teorema 3.7 Diberikan graph lobster L_n (q; r). Jika n≥ 2, q≥ 2 dan r = 1 maka dim(L_n(q; r')) = n(q — 1).

Bukti :

Berdasarkan Lemma 3.5, diperoleh gabungan sedikitnya (q — 1) vertex finger di setiap vertex backbone merupakan himpunan pemisah. Karena terdapat n vertex backbone maka banyak vertex finger sebagai anggota himpunan pemisah pada graph lobster tersebut sedikitnya adalah n(q — 1). Akan tetapi himpunan pemisah ini belum tentu merupakan himpunan pemisah minimum. Dengan demikian diperoleh bahwa

dim(Ln(q; 1)) ≤ n(q — 1)                        (3.1)

Selanjutnya berdasarkan Lemma 3.6, karena W ⊆ β maka kardinalitas himpunan W lebih kecil atau sama dengan kardinalitas himpunan β. Kardinalitas himpunan W adalah n(q — 1) sedangkan kardinalitas β adalah dim(L_n(q; 1)). Dengan demikian diperoleh bahwa

n⁽q — 1) ≤ dim(Ln(q; 1))                        (3.2)

Berdasarkan (3.1) dan (3.2) diperoleh dim(L_n(q; 1)) = n(q — 1). □

• 3.4    Dimensi Metrik Graph Lobster L_n(q; r) untuk n ≥ 2,q ≥ 1 dan r ≥ 2

Berikut ini diberikan lemma-lemma yang menyangkut himpunan pemisah pada graph lobster L_n(q; r) untuk n ≥ 2, q ≥ 1 dan r ≥ 2.

Lemma 3.8 Diberikan graph lobster L_n(q; r). Jika n≥ 2, q≥ 1 dan r ≥ 2 maka gabungan sedikitnya (r — 1) vertex finger di setiap vertex hand merupakan himpunan pemisah.

Bukti :

Tanpa mengurangi keumuman bukti diambil himpunan W = {f₁₁₁,f₁₁₂, —, ^f11(r—1)^, —^{, f}12(r—1), — ^{, f}1q(r—1)^{, f}211^{, f}212^, - ^{, f}21(r—1)^, - ^{, f}22(r—1)^, - ^{, f}2q(r—1), —^, f_nq(_r—1)} pada graph lobster L_n(q; r), diperoleh setiap vertex yang bukan himpunan W memiliki representasi jarak yang berbeda terhadap W, sedangkan berdasarkan Lemma 3.2 setiap vertex pada himpunan W memiliki representasi

jarak yang berbeda terhadap W. Lebih lanjut lagi, misalkan himpunan W digabungkan dengan himpunan Y yang anggota-anggotanya merupakan vertexvertex yang bukan di W, notasikan dengan W', maka W = WuY. Berdasarkan Lemma 3.2, setiap anggota W' mempunyai representasi jarak yang berbeda terhadap W'. Di lain pihak, berdasarkan hasil terdahulu, bahwa setiap vertex pada graph lobster L_n (q; r) dengan n≥ 2, q≥ 1 dan r ≥ 2 yang bukan anggota W memiliki representasi jarak yang berbeda terhadap W, maka setiap vertex pada graph lobster tersebut yang bukan anggota W' memiliki representasi jarak yang berbeda terhadap W'. Oleh karena itu, W' merupakan himpunan pemisah. Jadi gabungan sedikitnya (r — 1) vertex finger di setiap vertex hand merupakan himpunan pemisah.

Lemma 3.9 Diberikan graph lobster L_n(q; r). Jika n≥ 2, q ≥ 1 dan r ≥ 2 maka gabungan (r — 1) vertex finger di setiap vertex hand adalah himpunan bagian dari himpunan pemisah minimum (β) dari graph lobster tersebut.

Bukti :

Diambil gabungan (r — 1) vertex finger di setiap vertex hand yaitu ^w = {^f111^{, f}112^, — ^, f11(r-1)> ■■■^, f12(r-1)> ■■■^, f1q(r-1)> ^f211^,f212^, ■■■^, f21(r-1)> —> f₂₂(r_—1), —, f_2q(r_—1), —, f_nq(_r-1)}, diperoleh juga kardinalitas himpunan W adalah nq(r — 1). Berdasarkan Lemma 3.8, W merupakan himpunan pemisah. Akan ditunjukkan bahwa W ⊆ β. Andaikan W bukan himpunan bagian dari β. Dengan kata lain, terdapat vertex finger yang merupakan anggota di W tetapi bukan merupakan anggota di β. Tanpa mengurangi keumuman bukti, misalkan vertex tersebut vertex finger f₁₁₁ atau f₁₁₁ ∉ β. Diperoleh bahwa terdapat vertex yang memiliki representasi jarak yang sama, yaitu

r(f111 ∖β) =  r(f11_r∣β)

Hal ini berarti β bukan merupakan himpunan pemisah minimum. Terjadi kontradiksi, oleh karena itu f₁₁₁ ∈ β. Jadi W ⊆ β.∏

Berdasarkan Lemma 3.5 dan Lemma 3.6 diperoleh teorema yang menyangkut dimensi metrik pada graph lobster L_n (q; r) untuk n ≥ 2, q ≥ 1 dan r ≥ 2.

Teorema 3.10 Diberikan graph lobster L_n(q; r). Jika n≥ 2, q ≥ 1 dan r ≥ 2 maka dim[L_n(q; r)) = nq(r — 1).

Bukti :

Berdasarkan Lemma 3.8 diperoleh gabungan sedikitnya (r — 1) vertex finger di setiap vertex hand merupakan himpunan pemisah. Karena terdapat q vertex hand di setiap vertex backbone maka banyak vertex finger sebagai anggota himpunan pemisah pada graph lobster tersebut adalah nq(r — 1). Akan tetapi himpunan pemisah ini belum tentu merupakan himpunan pemisah minimum. Dengan demikian diperoleh bahwa

dim(L_n(q; r)) ≤ nq(r — 1)                            (3.3)

Selanjutnya berdasarkan Lemma 3.9, karena W ⊆ β maka kardinalitas himpunan W lebih kecil atau sama dengan kardinalitas himpunan β. Kardinalitas himpunan W adalah nq(r — 1) sedangkan kardinalitas β adalah dim(L_n(q; r)). Dengan demikian diperoleh bahwa

nq(r — 1) ≤ dim(L_n(q; r))                            (3.4)

Berdasarkan (3.3) dan (3.4) diperoleh dim(L_n(q; r)) = nq(r — 1).

• 4.    Kesimpulan

Berdasarkan pembahasan mengenai dimensi metrik graph lobster L_n (q; r) dengan t = 2, maka dapat disimpulkan dimensi metrik graph lobster L_n (q; r)

untuk n = 2, q = 1 dan r = 1 adalah 1, dimensi metrik graph lobster L_n (q; r)

untuk n >2, q = 1 dan r = 1 adalah 2, dimensi metrik graph lobster L_n (q; r)

untuk n ≥ 2, q ≥ 2 dan r = 1 adalah n(q — 1), dan dimensi metrik graph lobster

L_n (q; r) dengan n ≥ 2, q ≥ 2 dan r ≥ 2 adalah nq(r — 1).

Daftar Pustaka

• [1]    Beerliova Z., Eberhard F., Erlebach T., Hall A., Hoffmann M., Mihalak M. dan Ram L.S. 2006. Network Dicovery and Verification. IEEE Journal On Selected Areas in Communications. 24(12). p.2168-2181.

• [2]    Caceres J., Hernando C., Mora M, Pelayo I.M., Puertas M.L., Seara C., dan Wood D. R. 2007. On The Metric Dimension of Cartesian Products of Graphs. SIAM Journal on Discrete Mathematics. 21(2). p.423-441.

• [3]    Harary, F. dan Melter, R. A. 1976. On The Metric Dimension of A Graph. Ars Combinatoria. 2. p.191–195

• [4]    Khan, N., Pal, A. dan Pal, M. 2009. Edge Colouring of Cactus Graphs. AMO -Advanced Modeling and Optimization. 11(4).

• [5]    Khuller, S., Raghavachari, B., dan Rosenfeld, A. Landmarks in Graphs. Discrete Applied Mathematics. 70(3). p.217-229.

• [6]    Sebo, A. dan Tannier, E. 2004. On Metric Generators of Graphs. Mathematics of Operations Research. 29(2). p.383-393.

48