IMPLEMENTASI ALGORITMA DIJKSTRA DALAM MENENTUKAN RUTE TERPENDEK BIS TRANSJAKARTA DALAM MENGUNJUNGI 5 DESTINASI WISATA POPULER DI JAKARTA

E-Jurnal Matematika Vol. 9(4), November 2020, pp. 265-271

DOI: https://doi.org/10.24843/MTK.2020.v09.i04.p307

ISSN: 2303-1751

IMPLEMENTASI ALGORITMA DIJKSTRA DALAM MENENTUKAN RUTE TERPENDEK BIS TRANSJAKARTA DALAM MENGUNJUNGI 5 DESTINASI WISATA POPULER DI JAKARTA

Patricia Josephine Barek Baba Tapobali^1§, Cyrenia Novella Krisnamurti²

• ¹Program Studi Pendidikan Matematika, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma [Email: [email protected]]

• ²Program Studi Pendidikan Matematika, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma [Email: [email protected]]

^§Corresponding Author

ABSTRACT

This study shows the Dijkstra Algorithm process in determining the shortest Transjakarta bus route connecting 5 popular tourist destinations in Jakarta, namely; Ragunan Wildlife Park, Beautiful Indonesia Miniature Park, National Monument, Old Town, and Ancol Dreamland. Based on the analysis of the data obtained by the 5 shortest routes in visiting 5 popular tourist destinations in Jakarta with the initial position is a different tourist destination, namely; (1) TMII → Monas → City → Ancol → Ragunan with the length of the Transjakarta bus lane is 57.6 kilometers. (2) Ragunan → Monas → City → Ancol → TMII with the length of the Transjakarta bus lane is 47.38 kilometers. (3) Monas → City → Ancol → Ragunan → TMII with the length of the Transjakarta bus lane is 53.86 kilometers. (4) City → Ancol → Monas → Ragunan → TMII with the length of the Transjakarta bus lane is 49.46 kilometers. (5) Ancol → City → Monas → Ragunan → TMII with the length of the Transjakarta bus lane is 46.41 kilometers.

Keywords:  Algoritma Dijkstra, Destinasi Wisata Populer, Graf, Rute Bis Transjakarta

• 1.    PENDAHULUAN

DKI Jakarta adalah salah satu kota di Indonesia yang kaya akan objek wisatanya. Untuk mengunjungi wisata-wisata yang ada di Jakarta, para wisatawan lokal maupun non lokal kerap kali menggunakan transportasi umum Transjakarta sebagai pilihan transportasi bertamasya keliling Jakarta (Liputan6.com, 2017). Untuk menggunakan transportasi umum Transjakarta dalam mengunjungi destinasi-destinasi wisata yang diinginkan, para wisatawan perlu mengetahui rute bis transjakarta terpendek dalam mengunjungi destinasi-destinasi wisata tersebut agar dapat lebih menghemat waktu. PT Transportasi Jakarta menyediakan Peta Jaringan Transjakarta pada setiap halte bis Transjakarta dan situs resmi transjakarta.co.id agar dapat mempermudah wisatawan dalam mengetahui posisi mereka berada dengan posisi destinasi wisata yang akan dikunjungi. Namun, pada peta jaringan tersebut terdapat lebih dari satu rute untuk menuju tempat tujuan dari posisi awal

wisatawan berada sedangkan pada peta jaringan tersebut belum dijelaskan manakah rute yang terpendek, sehingga wisatawan kurang dapat mengetahui manakah rute terpendek untuk mengunjungi destinasi-destinasi wisata yang diinginkan.

Pada penelitian ini, akan mencoba untuk menentukan rute terpendek untuk mengunjungi 5 destinasi wisata populer di Jakarta. Tempat wisata popular di Jakarta yang menurut Badan Pusat Statistik tahun 2017 yaitu Taman Margasatwa Ragunan, Taman Mini Indonesia Indah, Monumen Nasional, Kawasan Kota Tua, dan Taman Impian Jaya Ancol, dengan menggunakan transportasi publik Transjakarta. Penelitian ini akan memberikan hasil berupa rute bis Transjakarta terpendek dalam mengunjungi 5 destinasi wisata populer tersebut dengan posisi-posisi awal merupakan destinasi wisata yang berbeda.

Algoritma Djikstra dapat digunakan dalam menentukan rute terpendek bis Transjakarta

dalam mengunjungi suatu lokasi ke lokasi lain, yaitu dengan mengubah rute bis Transjakarta kedalam simbol-simbol matematika yang dapat dihitung dan dianalisis secara matematis. Dalam menentukan rute terpendek dari suatu jaringan transportasi, terdapat beberapa algoritma yang dapat digunakan antara lain; Algoritma Dijkstra, Algoritma Floyd-Warshall, dan Algoritma Bellman-Ford (Susani, 2012). Penelitian ini menggunakan Algoritma Dijkstra karena kesederhanaan algoritmanya yang mudah dipahami dibandingkan algoritma Floyd-Warshall dan Algoritma Bellman-Ford, estimasi waktu yang dibutuhkan dalam menjalankan program lebih cepat dibandingkan dengan Algoritma Floyd-Warshall, label pada graf yang merepresentasikan rute bis Transjakarta yang menghubungkan 5 destinasi wisata tersebut selalu merupakan bilangan tak negatif sehingga Algoritma Dijkstra lebih tepat untuk digunakan daripada Algoritma BellmanFord yang digunakan untuk graf yang memiliki label negatif dengan efisiensi waktu yang lebih lama (Nawagusti dkk, 2018). Oleh sebab itu, penelitian ini akan menggunakan Algoritma Dijkstra untuk menentukan rute terpendek bis Transjakarta dalam mengunjungi 5 destinasi wisata populer tersebut dengan menginterpretasikan rute bis Transjakarta yang menghubungkan 5 destinasi wisata tersebut kedalam suatu graf yang selanjutnya akan dianalisis menggunakan Algoritma Dijkstra.

Pokok permasalahan dalam penelitian ini adalah dibutuhkannya informasi untuk memudahkan wisatawan agar mengetahui rute terpendek bis Transjakarta dalam mengunjungi Taman Margasatwa Ragunan Taman Mini Indonesia Indah, Monumen Nasional, Kawasan Kota Tua, dan Taman impian Jaya Ancol dengan menggunakan Algoritma Dijkstra. Untuk mendukung penelitian ini terlebih dahulu merepresentasikan destinasi wisata dan rute bis Transjakarta dalam bentuk graf.

Algoritma Djikstra merupakan salah satu topic dalam Graf. Untuk membahas lebih dalam terkait algoritma Djiksta terlebih dahulu dibahas tentang Graf. Suatu Graf G(V,E) adalah himpunan yang terdiri dari himpunan V yaitu himpunan tak kosong titik-titik yang elemennya disebut Titik, dan himpunan garis-garis yang elemennya disebut Sisi (Siang, 2011: 276). Sebuah sisi yang menghubungkan satu titik disebut Loop, sedangkan dua sisi berbeda yang menghubungkan satu titik yang sama disebut Sisi Paralel (Wilson, 2009:08).

Graf yang tidak memiliki sisi paralel tergolong sebagai Graf Sederhana, sedangkan Graf Tak Sederhana adalah graf yang memiliki sisi paralel dan Loop (Siang, 2011:279). Jika dibedakan berdasarkan labelnya, graf terbagi menjadi dua yaitu Graf berlabel, graf yang seluruh sisinya memiliki label yaitu suatu bilangan Riil yang menyatakan bobot hubungan dari dua titik yang dihubungkan, dan Graf Tak Berlabel yaitu graf yang semua sisi pada graf tersebut tidak memiliki label (Siang, 2011:276). Jika dibedakan berdasarkan arah dari sisi-sisi pada graf, graf dibedakan menjadi dua yaitu Graf Berarah, graf yang semua sisi pada graf tersebut memiliki arah yang menunjukkan titik asal dan titik tujuan, dan Graf Tak Berarah yaitu graf yang semua sisi-sisinya tidak memiliki arah (Siang, 2011:276). Suatu Lintasan dari titik v ke titik w pada graf G ( V,E) adalah barisan titik berhubungan dan sisi secara berselang-seling (Siang, 2011:283).

Matriks adalah susunan bilangan-bilangan yang disusun dalam bentuk persegi panjang dan diatur menurut baris dan kolom (Sulistyono, 2007: 59). Matriks dapat merepresentasikan suatu graf. Menurut Siang (2011: 286), graf yang diubah kedalam bentuk matriks dapat mempermudah perhitungan-perhitungan yang diperlukan, dan matriks yang digunakan untuk merepresentasikan suatu graf pada umumnya adalah Matriks Hubung atau Adjacency Matrix. Matriks hubung adalah matriks yang setiap elemen-elemennya adalah bobot hubungan antara titik pada baris dan titik pada kolomnya. Matriks hubung yang merepresentasikan suatu graf memiliki jumlah baris dan kolom yang sama dengan jumlah titik pada graf tersebut. Misalkan A_nnn adalah matriks berordo n× n, elemen matriks A yaitu a _i j dengan i ,j = 1,2,3,..., n. Elemen-elemen dari matriks hubung merepresentasikan hubungan antara baris ke- i dan kolom ke-j label sisi yang menghubungkan v t dan v_j-. Apabila suatu matriks adalah representasi dari graf tak berarah, maka matriks hubung yang dibentuk adalah matriks simetris yaitu a j = Cj t , ∀ i ,J'. Menurut Siang (2011: 299), Algoritma Dijkstra adalah algoritma yang ditemukan oleh Edsger W. Dijkstra, dan digunakan untuk menentukan jalur terpendek antara dua titik pada suatu graf. Misalkan G adalah graf berlabel (berarah ataupun tidak berarah) dengan titik-titik V(G) = { v₁ ,v₂ ,v₃ ,.,v_n} dan jalur terpendek yang dicari adalah jalur dari v₁ ke v_n, maka

Algoritma Dijkstra dimulai dari titik V₁. Dalam iterasinya, Algoritma Dijkstra akan mencari satu titik yang terhubung dengan V₁ dan memiliki label sisi yang paling kecil diantara titik lainnya yang juga terhubung dengan v ₁. Selanjutnya titik yang terpilih pada setiap iterasi akan dipisahkan (disebut titik permanen) dan titik tersebut tidak diperhatikan lagi pada iterasi-iterasi berikutnya. Misalkan V(G) adalah himpunan titik yang ada pada graf G yaitu V = { v₁,v₂ , v₃,...,v_n}, L merupakan himpunan titik pada V(G) yang sudah terpilih menjadi titik permanen, D(Vj) merupakan jumlah bobot lintasan terkecil dari V₁ ke V₇- , W merupakan matriks hubung yang merepresentasikan graf, dan W( i ,j ) adalah bobot sisi dari v_i ke Vj.

• 2.    METODE PENELITIAN

Penelitian ini merupakan penelitian terapan. Menurut Nawawi dan Martini (2015 : 11) menyatakan bahwa penelitian terapan adalah suatu kegiatan ilmiah yang mengungkapkan gejala alama maupun gelaja social yang terjadi dalam masyarakat, di mana dipandan perlu untuk memperbaiki suatu kejadain yang mengalami kelemahan. Peneliti melakukan penerapan dari Algoritma Dijkstra untuk menentukan lintasan terpendek bis Transjakarta dalam mengunjungi 5 destinasi wisata populer di Jakarta. Data 5 destinasi wisata populer tersebut menurut data Badan Pusat Statistik DKI Jakarta tahun 2017 adalah Taman Margasatwa Ragunan, Taman Mini Indonesia Indah, Monumen Nasional, Kawasan Kota Tua, dan Taman Impian Jaya Ancol. Objek dari penelitian ini adalah Rute bis Transjakarta yang menghubungkan 5 destinasi wisata populer tersebut.

Variabel yang digunakan dalam penelitian ini ada dua, yaitu variabel bebas dan variabel terikat. Variabel bebas dari penelitian ini adalah destinasi wisata pertama yang akan dikunjungi, sedangkan variabel terikat dari penelitian ini adalah rute terpendek bis Transjakarta dalam mengunjungi 5 destinasi wisata populer tersebut.

Teknik pengumpulan data yang digunakan dalam penelitian ini adalah menggunakan data Badan Pusat Statistik DKI Jakarta untuk memperoleh 5 destinasi wisata di Jakarta dengan jumlah pengunjung terbanyak pada tahun 2015, menggunakan situs resmi PT.

Transportasi Jakarta untuk memperoleh Peta Jaringan Transjakarta, dan Google Maps untuk memperoleh data panjang jalur bis Transjakarta yang menghubungkan halte-halte bis Transjakarta. Teknik analisis data yang dilakukan dalam penelitian ini ada dua tahap yaitu: (1) menganalisis data untuk memodelkan rute bis Transjakarta yang menghubungkan 5 destinasi wisata populer di Jakarta kedalam suatu Graf Berarah dan Berlabel dimana titik pada graf merepresentasikan halte-halte bis Transjakarta, sisi pada graf merepresentasikan jalur bis Transjakarta, arah dari sisinya menyatakan jalur bis Transjakarta yang tersedia, dan label pada sisinya menyatakan panjang jalur bis Transjakarta (2) menganalisis data menggunakan Algoritm Dijkstra untuk memperoleh rute bis Transjakarta terpendek dalam mengunjungi 5 destinasi wisata populer di Jakarta.

Untuk menentukan jalur terpendek dari V_a ke V_n , maka langkah kerja Algoritma Dijkstra menurut Jong Jek Siang (2011: 299) adalah sebagai berikut:

• 1.    Menentukan V_a sebagai titik awal dan V_n sebagai titik akhir.

• 2.    Menentukan tabel representasi dari graf.

• 3.    Membuat matriks hubung W.

• 4.    Untuk iterasi pertama, lakukan:

• a.    Inisialisasi :

• •    L = {  }

• •    VGG= = {V1,V2,V₃, ^,Vn^}

• b.    Titik awal adalah V_a maka lakukan

D( v= — (0 '^j.= ^a, ∀ v,- ∈ V( G=. (∞ ,j ≠ a ^{1 v j}

• c.    ∀   ∈  ( ), tentukan ( ) terkecil,

maka titik permanen adalah .

• d.    L = LU { v_p}

• e.    Jika v_n ∈ L maka iterasi berhenti, jika v_n ∉ L maka iterasi berlanjut.

• 5.    Untuk iterasi kedua dan seterusnya, lakukan:

• a.    Inisialisasi :

• •   —

• • V(G) — V(G)-{ v_p}

• b.    Selanjutnya    ∀ V₁- ∈ V( G), lakukan

D ( Vj) — min(β(vj),D(vp) + W (p ,j)).

• c.    Kemudian ∀ v₁∙ ∈ V( G), tentukan D( v= terkecil, maka titik permanen adalah ^V1.

• d.    Diperoleh L = LU { v_p}

• e.    Jika ∈ maka iterasi berhenti, jika v_n ∉ L maka iterasi berlanjut.

• 6.    Tuliskan D(v_j∙) untuk j = 1,2,3, ...,n pada setiap iterasi diatas kedalam tabel.

• 7.    Tentukan lintasan terpendeknya dengan mendaftar titik permanen pada tabel diatas mulai dari iterasi terakhir hingga iterasi pertama. Perhatikan titik permanen v_j∙ pada iterasi ke- i, apabila D( v_j∙) pada iterasi ke- i mengalami penurunan dibandingkan D( v_j∙) pada iterasi sebelumnya, maka titik permanen pada iterasi ke- i tersebut merupakan jalur yang harus dilalui.

• 8.    Panjang Lintasan dari v _a ke v_n adalah D( v_p) pada iterasi terakhir.

• 9.    Interpretasi.

• 3.    HASIL DAN PEMBAHASAN

Dari peta jaringan Transjakarta, pertama menentukan rute bis Transjakarta yang menghubungkan 5 destinasi wisata populer yang terpilih, serta panjang lintasan jalur bis Transjakarta yang berada pada rute tersebut. Peta bis Transjakarta yang menghubungkan 5 destinasi wisata populer yang terpilih dapat dilakukan dengan menggambarkan kembali peta jaringan Transjakarta dengan rute yang hanya menghubungkan 5 destinasi wisata terpilih. Sedangkan untuk menentukan panjang lintasan jalur bis Transjakarta dapat digunakan dengan mendaftar halte-halte bis Transjakarta yang berada pada rute tersebut. Selanjutnya menentukan panjang lintasan jalur bis Transjakarta antara dua halte yang berada pada jalur yang sama.

Halte bis Transjakarta terdekat dari Taman Margasatwa Ragunan adalah Halte Ragunan, halte bis Transjakarta terdekat dari Taman Mini Indonesia Indah adalah Halte TMII, halte bis Transjakarta terdekat dari Monumen Nasional adalah Halte Monas, halte bis Transjakarta terdekat dari Kawasan Kota Tua adalah Halte Kota, dan halte bis Transjakarta terdekat dari Taman Impian Jaya Ancol adalah Halte Ancol, sehingga diperoleh rute yang menghubungkan kelima destinasi wisata populer beserta nomor bis Transjakarta yang melalui rute tersebut adalah sebagai berikut:

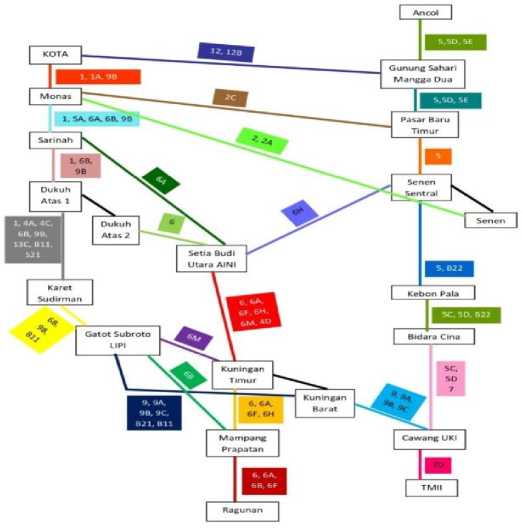
Gambar 1. Peta Jaringan Bis Transjakarta yang Menghubungkan 5 Destinasi Wisata Populer di Jakarta

Untuk menentukan panjang jalur bis Transjakarta yang ada pada peta tersebut, peneliti menggunakan Google Maps sehingga diperoeh data pada Tabel 1.

Selanjutnya, peta jaringan transjakarta yang menghubungkan 5 destinasi wisata populer tersebut direpresentasikan kedalam graf G. Simbol-simbol matematika adalah dengan merepresentasikan halte-halte bis Transjakarta menjadi titik-titik pada graf, jalur bis transjakarta yang tersedia menjadi sisi yang berarah pada graf, dan panjang jalur bis transjakarta menjadi label pada sisi dalam graf tersebut, maka selanjutnya dapat dibentuk suatu graf berarah dan berlabel yaitu graf G(V,E) yang merepresentasikan rute bis Transjakarta yang menghubungkan 5 destinasi wisata populer di Jakarta. Penamaan titik-titik pada graf dijelaskan pada Tabel 2.

Tabel 1. Panjang Jalur Bis Transjakarta

Awal	Tujuan	Panjang Jalur Bis Transjakarta (meter)
Ragunan	Mampang Prapatan	7450
Mampang Prapatan	Gatot Subroto LIPI	2150
Mampang Prapatan	Kuningan Timur	950
TMII	Cawang UKI	11810
Cawang UKI	TMII	6900
Cawang UKI	Kuningan Barat	7500
Cawang UKI	Bidara Cina	3900
Kuningan Barat	Gatot Subroto LIPI	1700
Kuningan Barat	Kuningan Timur	130
Kuningan Timur	Gatot Subroto LIPI	1850
Kuningan Timur	Setiabudi Utara AINI	3230
Gatot Subroto LIPI	Karet Sudirman	2600
Bidara Cina	Kebon Pala (Via Kp. Melayu)	2050
Karet Sudirman	Dukuh Atas 1	800
Kebon Pala	Bidara Cina (Via Kp. Melayu)	2300
Kebon Pala	Senen Sentral	4550
Setiabudi Utara AINI	Kuningan Timur	3230
Setiabudi Utara AINI	Dukuh Atas 2	3200
Setiabudi Utara AINI	Sarinah	2600
Setiabudi Utara AINI	Senen Sentral	6990
Dukuh Atas 1	Karet Sudirman	800
Dukuh Atas 1	Dukuh Atas 2	300
Dukuh Atas 1	Sarinah	2000
Dukuh Atas 2	Dukuh Atas 1	300
Dukuh Atas 2	Setiabudi Utara AINI	1310
Senen Sentral	Setiabudi Utara AINI	10140
Senen Sentral	Senen	56
Senen Sentral	Pasar Baru Timur	2200
Senen	Monas	6000
Sarinah	Setiabudi Utara AINI	2600
Sarinah	Monas	1400
Monas	Senen	3300
Monas	Pasar Baru Timur	4300
Monas	Kota	4400
Kota	Gunung Sahari Mangga Dua	2300
Pasar Baru Timur	Senen Sentral	2200
Pasar Baru Timur	Monas	3400
Pasar Baru Timur	Gunung Sahari Mangga Dua	2900
Ancol	Gunung Sahari Mangga Dua	1150

Tabel 2. Penamaan Titik pada Graf G( V , E)

Nama Titik	Nama Halte Bis Transjakarta
Vl	Kuningan Barat
V2	Cawang UKI
V3	TMII
V4	Gatot Subroto LIPI
V5	Kuningan Timur
V6	Bidara Cina
V7	Kebon Pala
V8	Karet Sudirman
V9	Ragunan
VlO	Mampang Prapatan
Vll	Setiabudi Utara AINI
V12	Senen Sentral
Vi3	Dukuh Atas 1
Vi4	Dukuh Atas 2
VlS	Senen
Vi6	Sarinah
V17	Monas
VlS	Pasar Baru Timur
V19	Kota
V2O	Gunung Sahari Mangga Dua
V2I	Ancol

Dengan demikian, Graf yang merepresentasikan rute bis Transjakarta yang menghubungkan 5 destinasi wisata populer di Jakarta dituliskan sebagai Graf Tak Sederhana, Berarah, dan Berlabel yang selanjutnya disebut Graf G(V,E).

Untuk menentukan rute terpendek bis Transjakarta dalam mengunjungi 5 destinasi wisata populer di Jakarta terdsebut, perlu ditentukan rute terpendek bis Transjakarta dari halte-halte bis Transjakarta terdekat dari destinasi wisata, menuju halte-halte bis Transjakarta terdekat dari destinasi wisata lainnya menggunakan Algoritma Dijkstra sehingga dapat diperoleh panjang lintasannya sebagai berikut:

Tabel 3. Panjang Jalur bis Transjakarta antar Destinasi Wisata

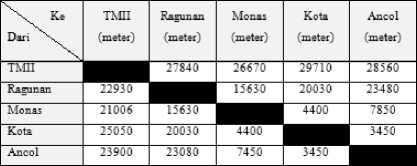
Kemudian tentukan rute bis Transjakarta terpendek dalam mengunjungi 5 destinasi wisata populer di Jakarta dengan posisi awal adalah masing-masing destinasi wisata dengan proses sebagai berikut:

• 1.    Untuk iterasi pertama lakukan:

• •    Tl = Destinasi wisata pertama yang dikunjungi

• •    Membuat tabel panjang lintasan bis Transjakarta dengan menghapus kolom yang memuat A.

• •    Pilih halte B yang memiliki panjang lintasan terpendek terhadap halte A .

• •    Rute terdekat: A → B

• 2.    Untuk iterasi kedua lakukan:

• •    Membuat tabel panjang lintasan bis Transjakarta dengan menghapus kolom yang memuat A dan B.

• •    Pilih halte C yang memiliki panjang lintasan terpendek terhadap halte B.

• •    Rute terdekat: A → B → C

• 3.    Untuk iterasi ketiga, lakukan:

• •    Membuat tabel panjang lintasan bis Transjakarta dengan menghapus kolom yang memuat A , B , dan C.

• •    Pilih halte D yang memiliki panjang lintasan terpendek terhadap halte .

• •    Rute terdekat:  →  →  →

• 4.    Untuk iterasi keempat, lakukan:

• •    Membuat tabel panjang lintasan bis Transjakarta dengan menghapus kolom yang memuat ,  ,  , dan .

• •    Pilih halte yang memiliki panjang lintasan terpendek terhadap halte .

• •    Rute terdekat:  →  →  →  →

Dengan menggunakan algoritma diatas, diperoleh 5 rute bis Transjakarta yang menghubungkan 5 destinasi wisata populer di Jakarta dengan posisi awal merupakan halte bis transjakarta terdekat dari destinasi wisata yang berbeda yaitu rute terpendek pertama dimulai dari HalteTMII, rute terpendek kedua dimulai dari Halte Ragunan, rute terpendek ketiga dimulai dari Halte Monas, rute terpendek keempat dimulai dari Halte Kota, dan rute terpendek kelima dimulai dari Halte Ancol. Berikut adalah 5 rute bis Transjakarta dalam mengunjungi 5 destinasi wisata populer di Jakarta dengan posisi awal merupakan halte bis Transjakarta terdekat dari destinasi wisata yang berbeda-beda beserta panjang lintasannya.

Tabel 4. Rute Terpendek dan Panjang Lintasan

Rute	Rute Destinasi Wisata	Panjang Lintasan (Km)
1	TMH — Monas — Kota — Ancol — Ragtrun	57,6
2	Ragunan — Monas — Kota — Ancol — TM ∏	47J8
3	Monas — Kota — Ancol — Ragman — TMII	53.86
4	Kota — Ancol — Monas —Ragman — TMΠ	49.46
5	Ancol — Kota — Monas — Raaynan- TMΠ.	46,41

• 4.    KESIMPULAN DAN SARAN

Berdasarkan penelitian yang telah dilakukan, dapat disimpulkan bahwa (1) Hasil memodelkan rute bis Transjakarta yang menghubungkan 5 destinasi wisata populer di Jakarta ke dalam bentuk graf yaitu :

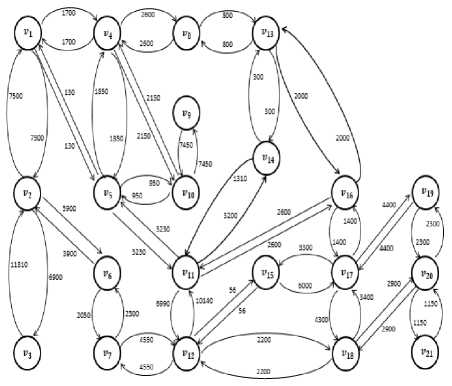
Gambar 2. Graf G ( V , E)

.(2) cara menentuka rute terpendek bis Transjakarta dalam mengunjungi 5 destinasi wisata populer di Jakarta adalah dengan menggunakan Algoritma Dijkstra untuk menentukan rute terpendek dari setiap halte bis Transjakarta terdekat dengan masing-masing destinasi wisata, ke setiap halte bis Transjakarta terdekat dengan masing-masing destinasi wisata lainnya, kemudian dengan menggunakan rute dan panjang lintasan bis Transjakarta yang diperoleh, menentukan urutan destinasi wisata yang terpilih sehingga diperoleh 5 rute bis Transjakarta yang dapat dilakukan dalam mengunjungi 5 destinasi wisata populer di Jakarta dengan posisi awal merupakan 5 halte bis Transjakarta terdekat dengan destinasi wisata.

DAFTAR PUSTAKA

Arikunto, Suharsimi. 2006. Prosedur Penelitian Suatu Pendekatan Praktek. Jakarta: PT. Rineka Cipta

Arikunto, Suharsimi. 2010. Managemen Penelitian Edisi Revisi. Jakarta: Rineka Cipta

Badan Pusat Statistik DKI Jakarta. Jumlah Kunjungan Wisatawan ke Obyek Wisata Unggulan Menurut Lokasi Tahun 20112015. Diakses pada tanggal 28 Januari 2019                                dari

https://jakarta.bps.go.id/statictable/2017/01/ 30/158/jumlah-kunjungan-wisatawan-ke-obyek-wisata-unggulan-menurut-lokasi-2011-2015.html

Fauzi, Imron. 2011. Penggunaan Algoritma Dijkstra dalam Pencarian Rute Tercepat dan Terpendek (Studi Kasus pada Jalan raya antara Wilayah Blok M dan Kota). Skripsi Program Studi Teknik Informatika, Universitas UIN Syarif Hidayatullah, Jakarta.

Kountur, Ronny. 2003. Metode Penelitian untuk Penulisan Skripsi dan Tesis. Jakarta: Penerbit PPM.

Liputan6.com. 2017. Liburan Tahun Baru, Transjakarta jadi Transportasi Favorit warga. Diakses tanggal 1 Juni 2019 dari https://www.liputan6.com/citizen6/read/26 93270/liburan-tahun-baru-transjakarta-jadi-transportasi-favorit-warga

Narbuko, Cholid dan H. Abu Achmadi. 2007. Metodologi Penelitian. Jakarta:   BUMI

AKSARA

Nawagusti, Vera Apriliani dkk. 2018. Penentuan Rute Terpendek pada Optimalisasi Jalur Pendistribusian Barang di PT.X dengan Menerapkan Algoritma Floyd-Warshall. Seminar Nasional Inovasi dan Aplilkasi Teknologi di Industri 2018: ISSN 2085-4218. ITN Malang: 3 Februari 2018.

Nawawi, H. Hadari & H. Mimi Martini. 2005. Penelitian Terapan. Yogyakarta: Gadjah Mada University Press.

PT. Transportasi Jakarta. 2017. Peta Jaringan Transjakarta. Diakses tanggal 18 Februari 2019 dari http://transjakarta.co.id/peta-rute/

Setiadji. ---.Pengantar Teori Graf. Bahan Kuliah Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Gadjah Mada, Yogyakarta.

Siang, Jong Jek. 2011. Riset Operasi Dalam Pendekatan Logaritmis. Jakarta: Penerbit Andi.

Sulistyono. 2007. Seri Pendalaman Materi Matematika SMA dan MA. Jakarta: Penerbit Erlangga.

Suryadi H.S. 1994. Teori Graf Dasar. Jakarta: Penerbit Gunadarma.

Susani, Indriyani Mulyawatik. 2012. Perbandingan Algoritma Dijkstra, Bellman-Ford, dan Floyd-Warshall untuk Mencari Rute terpendek (The Shortest Lintasan Problem). Skripsi Program Studi Matematika, Fakultas Sains dan Teknologi, Universitas Islam Negeri Sunan Kalijaga, Yogyakarta.

Wilson, Robin J. 2009. Pengantar Teori Graf Edisi Kelima. Jakarta: Penerbit Erlangga.

271