RUSSELL’S APPROXIMATION METHOD DAN IMPROVED VOGEL’S APPROXIMATION METHOD DALAM PENYELESAIAN MASALAH TRANSPORTASI
on
E-Jurnal Matematika Vol. 8(3), Agustus 2019, pp.184-193
DOI: https://doi.org/10.24843/MTK.2019.v08.i03.p251
ISSN: 2303-1751
RUSSELL’S APPROXIMATION METHOD DAN IMPROVED
VOGEL’S APPROXIMATION METHOD DALAM PENYELESAIAN MASALAH TRANSPORTASI
Ni Putu Intan Puspa Dewi1§, Ni Ketut Tari Tastrawati2, Kartika Sari3
-
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: intanpuspa315@gmail.com]
-
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: tastrawati@unud.ac.id]
-
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: sarikaartika@unud.ac.id]
§Corresponding Author
ABSTRACT
Distribution activities in company which related in distribution sometimes have a problems, one of the problems is transportation problem. To solve that problem can be used a transportation model to obtain the distribution route so the cost that come out is more minimum. The aim of this research is to compare the initial solution of RAM and IVAM and to know the distribution route in distribution of bottled water in the CV. Prasarana Fortuna Prima so obtained the minimum distribution costs after optimality test using MODI. The results showed that RAM gave a lower initial solution than IVAM and the initial solution of RAM was optimum after optimality test using MODI with a distribution routes is from depo Klungkung to Toko Bintang, Toko Subur, Toko Cahaya Melati, Toko Mawar Sari, and Coco Mart Ubud, from depo Kapal to CV. Sumber Jaya, Toko Sol Mandala, and Toko Kayana, from depo Mahendradatta to Toko Sinar Wangi and Toko Aris.
Keywords: Distribution, IVAM, MODI, RAM, Transportation Model
Model transportasi merupakan salah satu model yang dapat menyelesaikan permasalahan transportasi. Pada umumnya, permasalahan transportasi berkaitan dengan proses pendistribusian barang dari beberapa sumber produksi ke beberapa lokasi tujuan yang ditujukan untuk meminimalkan biaya transportasi (Hillier & Lieberman, 1994). Kegiatan distribusi dalam suatu perusahaan adalah kegiatan rutin yang dilakukan untuk menyalurkan barang dan jasa, misalnya perusahaan yang bergerak pada bidang produksi, jasa konstruksi, ekspedisi, pemasok, distributor, dan perusahaan lainnya (Hasibuan, 2017).
Setiap perusahaan yang bergerak pada bidang pendistribusian menginginkan pendistribusian barang dan jasa agar tepat waktu sampai lokasi tujuan dengan biaya yang minimum. Namun, ada beberapa masalah yang sering timbul dalam proses pendistribusian, antara lain pemilihan rute atau jalur dalam pendistribusian yang kurang tepat dan waktu yang diperlukan untuk mendistribusikan barang
dan jasa dari sumber produksi ke lokasi tujuan kurang optimal (Sari, 2014). Guna mengatasi permasalahan dalam proses pendistribusian tersebut, dapat digunakan model transportasi agar diperoleh rute atau jalur distribusi yang tepat sehingga biaya yang dikeluarkan lebih minimum, perusahaan mendapatkan keuntungan yang maksimal, dan kegiatan pendistribusian lebih efektif dan efisien.
Pada model transportasi terdapat beberapa metode untuk mendapatkan solusi awal, antara lain metode North West Corner (NWC), Least Cost (LC), Russell’s Approximation Method (RAM), dan Vogel’s Approximation Method (VAM). Selain metode tersebut ada metode pengembangan dari VAM yaitu Improved Vogel’s Approximation Method (IVAM). Namun tidak ada teori yang menjamin bahwa solusi awal merupakan solusi yang optimal. Oleh karena itu, untuk memperoleh hasil yang optimal, ada dua metode yang dapat digunakan yaitu metode Stepping Stone dan Modified Distribution (MODI) (Siswanto, 2007).
Sehubungan dengan penerapan model
transportasi, penelitian yang dilakukan oleh Korukoğlu dan Ballı (2011) menggunakan IVAM untuk mengoptimalkan biaya pendistribusian pada suatu kasus diperoleh hasil bahwa biaya yang diperoleh dari IVAM lebih minimum dan telah optimal daripada biaya yang diperoleh dari VAM. Selain itu, penelitian yang dilakukan oleh Nofrianto (2015) menggunakan VAM dan RAM untuk mengoptimalkan biaya pendistribusian air pada PDAM Kota Padang diperoleh hasil bahwa biaya yang diperoleh dari VAM dan RAM sama dan telah optimal. Kemudian penelitian yang dilakukan oleh Nahar (2018) menggunakan IVAM untuk mengoptimalkan biaya pendistribusian beras pada Perum BULOG Divre Medan diperoleh hasil bahwa biaya yang diperoleh dari IVAM lebih minimum dibandingkan dengan perhitungan yang dilakukan oleh Perum BULOG dan saat dilakukan uji optimalitas dengan MODI biaya yang diperoleh dari IVAM telah optimal.
Permasalahan transportasi juga dialami oleh CV. Prasarana Fortuna Prima. Selama ini CV. Prasarana Fortuna Prima tidak menggunakan metode khusus dalam mendistribusikan Air Minum Dalam Kemasan (AMDK). Perusahaan ini mendistribusikan AMDK secara langsung tanpa memperhatikan rute dari sumber ke lokasi tujuan. Permasalahan yang dialami tersebut dapat diselesaikan menggunakan model transportasi. Oleh karena itu, penelitian ini bertujuan untuk mengetahui perbandingan solusi awal dari RAM dan IVAM pada masalah pendistribusian AMDK di CV. Prasarana Fortuna Prima dan rute pendistribusian dari sumber ke lokasi tujuan sehingga diperoleh biaya pendistribusian yang minimum setelah dilakukan uji optimalitas menggunakan MODI.
Pada penelitian ini hanya membahas pendistribusian AMDK CLUB dalam kemasan dus 600 ml pada bulan Oktober sampai Desember 2018. Biaya yang dikeluarkan adalah biaya BBM, biaya dari pabrik ke depo diabaikan. Daerah pendistribusian yaitu daerah Denpasar, Badung, Gianyar, dan Klungkung. Diasumsikan akses jalan bisa dilalui semua kendaraan dan barang dapat diantar sekaligus dengan satu mobil box ke satu tempat tujuan. Perhitungan biaya menggunakan aturan pembulatan, jika angka dibelakang koma adalah angka 5 atau lebih maka dibulatkan ke atas, jika angka dibelakang koma kurang dari 5 maka dibulatkan ke bawah.
-
2. METODE PENELITIAN
Jenis dan Sumber Data
Data yang digunakan pada penelitian ini adalah data sekunder dalam bentuk data kuantitatif yaitu data banyaknya depo CV. Prasarana Fortuna Prima beserta persediaan AMDK 600 ml di masing-masing depo, permintaan AMDK 600 ml dari masing-masing lokasi tujuan, banyaknya AMDK 600 ml yang didistribusikan dari masing-masing depo ke masing-masing lokasi tujuan, serta biaya transportasi dalam mendistribusikan AMDK 600 ml dari masing-masing depo ke masing-masing lokasi tujuan. Semua data di atas merupakan data pada bulan Oktober sampai Desember 2018 yang diperoleh dari CV. Prasarana Fortuna Prima.
Variabel Penelitian
Variabel yang digunakan pada penelitian ini adalah jumlah persediaan AMDK 600 ml di masing-masing depo (ai), jumlah permintaan AMDK 600 ml di masing-masing tempat tujuan (bj), banyaknya AMDK 600 ml yang didistribusikan dari depo i ke tempat tujuan j (xij), dan biaya yang dikeluarkan dalam pendistribusian AMDK 600 ml dari depo i ke tempat tujuan j (c^) dengan i = 1,2,3 dan j = 1,2, ..,10. Indeks i dan j yang dimaksud adalah sebagai berikut:
Tabel 1. Nama Indeks i dan j
|
i |
Depo |
j |
Tempat Tujuan |
|
1 |
Klungkung |
1 |
Toko Bintang |
|
2 |
Toko Subur | ||
|
3 |
Toko Cahaya Melati | ||
|
2 |
Kapal |
4 |
Toko Mawar Sari |
|
5 |
Coco Mart Ubud | ||
|
6 |
CV Sumber Jaya | ||
|
3 |
Mahendradatta |
7 |
Toko Sinar Wangi |
|
8 |
Toko Sol Mandala | ||
|
9 |
Toko Aris | ||
|
10 |
Toko Kayana |
Metode Analisis Data
Adapun langkah-langkah analisis data adalah sebagai berikut:
-
1. Mengumpulkan data persediaan AMDK 600 ml di masing-masing depo, data permintaan AMDK 600 ml dari masing-masing tempat tujuan, banyaknya AMDK 600 ml yang didistribusikan dari masing-masing depo ke
masing-masing tempat tujuan, dan biaya transportasi dalam pendistribusian AMDK 600 ml dari masing-masing depo ke masing-masing tempat tujuan serta menghitung biaya distribusi per dus dan biaya rata-rata distribusi per dus pada bulan Oktober– Desember 2018.
-
2. Membentuk model transportasi yang seimbang (balanced transportation).
-
3. Membentuk fungsi tujuan dan fungsi
kendala.
-
4. Menghitung solusi awal dengan RAM dan IVAM.
-
5. Uji optimalitas dengan MODI.
-
6. Interpretasi hasil.
Langkah-langkah menghitung solusi awal dengan RAM (Siswanto, 2007):
-
1. Menentukan biaya distribusi tertinggi pada masing-masing baris ke-i ( ̅γ ) dan kolom ke-j ( ̅ i).
-
2. Menghitung selisih biaya distribusi setiap sel menggunakan rumus: ∆Cij- = - ̅i-
̅i.
-
3. Menentukan sel yang memiliki selisih biaya (∆ cij ) dengan negatif terbesar, kemudian dilakukan pengalokasian paling maksimum terhadap sel yang memiliki ∆ cij dengan negatif terbesar dengan memperhatikan permintaan dan penawaran yang paling minimum dimana sel tersebut berada.
-
4. Menghilangkan baris atau kolom yang telah dipenuhi. Baris atau kolom yang telah dipenuhi tidak dapat lagi digunakan untuk menentukan biaya distribusi tertinggi berikutnya.
-
5. Mengulangi langkah 1 sampai langkah 4 sampai sel-sel lain terisi penuh.
-
6. Menghitung total biaya minimum distribusi menggunakan rumus:
Z =∑i^i ∑7=1 CijXij = + c12x12 +
c13x13+⋯+CmnXmn
Sedangkan langkah-langkah menghitung solusi awal dengan IVAM (Korukoğlu & Ballı, 2011):
-
1. Menghitung nilai Total Opportunity Cost (TOC) dengan menjumlahkan hasil dari Row Opportunity Cost dan Column Opportunity Cost. Untuk menghitung Row Opportunity Cost, terlebih dahulu dicari biaya distribusi terendah untuk setiap baris kemudian kurangkan masing-masing biaya distribusi dengan biaya terendah pada baris yang sama. Untuk menghitung Column Opportunity Cost, terlebih dahulu dicari
biaya distribusi terendah untuk setiap kolom kemudian kurangkan masing-masing biaya distribusi dengan biaya terendah pada kolom yang sama.
-
2. Mencari selisih biaya terendah dengan biaya terendah berikutnya untuk setiap baris dan kolom yang sama. Biaya yang digunakan adalah biaya yang telah diperoleh pada langkah 1.
-
3. Memilih tiga selisih biaya dengan nilai yang terbesar dan mengalokasikan produk paling maksimum ke sel yang memiliki biaya terendah pada ketiga baris atau kolom yang terpilih. Jika terdapat nilai yang sama maka dapat dipilih secara sebarang. Dalam mengalokasikan produk kedalam tiga baris atau kolom yang terpilih, terlebih dahulu alokasikan produk ke baris atau kolom dengan selisih biaya terbesar di antara tiga selisih biaya tersebut dan alokasikan sesuai dengan permintaan dan penawaran paling minimum yang ada pada baris atau kolom yang terpilih.
-
4. Menghilangkan baris atau kolom yang telah diisi dan baris atau kolom tersebut tidak digunakan lagi untuk menghitung selisih biaya berikutnya.
-
5. Ulangi langkah 2 sampai langkah 4 sampai semua sel pada baris dan kolom teralokasi.
-
6. Setelah semua sel terisi kemudian menghitung total biaya minimum distribusi.
Setelah menghitung solusi awal dilanjutkan dengan uji optimalitas menggunakan MODI dengan langkah-langkah seperti berikut:
-
1. Memastikan jumlah sel dengan variabel dasar pada tabel yang diperoleh saat pemecahan awal sama dengan m+n-1, dengan m adalah jumlah baris dan n adalah jumlah kolom.
-
2. Menghitung nilai indeks pada masing-masing baris dan kolom menggunakan rumus: Ui + Vj = , untuk setiap variabel
dasar xij dengan menetapkan nilai U1 sama dengan nol. Ui merupakan nilai indeks baris ke-i, i=1,2,…,m dan vj merupakan nilai indeks kolom ke-j, j=1,2,…,n.
-
3. Menghitung besarnya nilai pada sel-sel yang kosong (opportunity cost) menggunakan rumus: ̅̅̅=cij - Ui - Vj .
-
4. Apabila seluruh nilai sel-sel yang kosong (nilai ̅̅̅) telah bernilai positif atau nol maka solusi minimum telah diperoleh. Apabila seluruh nilai sel-sel yang kosong (nilai ̅̅̅) masih ada yang bernilai negatif maka pilih
variabel masuk dengan memilih nilai clj yang paling negatif (negatif terbesar) kemudian dilanjutkan ke langkah 5.
-
5. Menentukan variabel keluar menggunakan jalur tertutup dengan memberi tanda positif pada sel kosong yang terpilih pada langkah 4 kemudian memberi tanda negatif, positif, negatif, dan seterusnya disesuaikan dengan arah jalur tertutup. Selanjutnya tambahkan dan kurangkan isi tabel dengan isi sel bertanda negatif yang memiliki nilai terkecil pada seluruh sel yang ada di jalur tertutup.
-
6. Ulangi langkah 2 sampai langkah 5 sampai semua nilai sel-sel yang kosong (nilai Cjj) bernilai positif atau nol.
-
7. Menghitung total biaya minimum.
-
8. Interpretasi hasil.
-
3. HASIL DAN PEMBAHASAN
Data Penelitian
Perusahaan ini memiliki tiga depo, yaitu depo Klungkung, depo Kapal, dan depo Mahendradatta. Pada penelitian ini hanya membahas pendistribusian ke beberapa toko yang berada di daerah Denpasar yaitu Toko Sinar Wangi dan Toko Kayana, di daerah Badung yaitu CV. Sumber Jaya, Toko Sol Mandala, dan Toko Aris, di daerah Gianyar yaitu Toko Mawar Sari dan Coco Mart Ubud, dan di daerah Klungkung yaitu Toko Bintang, Toko Subur, dan Toko Cahaya Melati. Biaya distribusi yang dikeluarkan untuk
mendistribusikan AMDK Club 600 ml dari masing-masing depo ke masing-masing tempat tujuan adalah biaya BBM.
Adapun persediaan AMDK 600 ml di masing-masing depo selama tiga bulan ( ai), permintaan AMDK 600 ml di masing-masing tempat tujuan pada bulan Oktober–Desember 2018 ( bj'), banyaknya AMDK 600 ml yang dikirimkan dari masing-masing depo ke masing-masing tempat tujuan (x^), biaya distribusi per dus dari bulan Oktober– Desember 2018, dan biaya rata-rata distribusi per dus (ctj) disajikan secara terurut pada Tabel 2, 3, 4, 5, dan 6.
Tabel 2. Persediaan Masing-masing Depo ( ai)
|
I |
Depo |
Persediaan (dus) |
|
1 |
Klungkung |
1293 |
|
2 |
Kapal |
4764 |
|
3 |
Mahendradatta |
4218 |
|
Jumlah |
10275 |
Tabel 3. Permintaan Masing-masing Tempat
Tujuan (bj)
|
j |
Tempat Tujuan |
Jumlah Permintaan (dus) |
|
1 |
Toko Bintang |
100 |
|
2 |
Toko Subur |
450 |
|
3 |
Toko Cahaya Melati |
272 |
|
4 |
Toko Mawar Sari |
90 |
|
5 |
Coco Mart Ubud |
65 |
|
6 |
CV Sumber Jaya |
1205 |
|
7 |
Toko Sinar Wangi |
705 |
|
8 |
Toko Sol Mandala |
450 |
|
9 |
Toko Aris |
457 |
|
10 |
Toko Kayana |
255 |
|
Total Permintaan |
4049 |
Tabel 4. Distribusi Masing-masing Depo ke
Masing-masing Tempat Tujuan (x y)
|
I |
Sumber |
j |
Tempat Tujuan |
Total (dus) |
|
1 |
Depo Klungk ung |
1 |
Toko Bintang |
100 |
|
2 |
Toko Subur |
450 | ||
|
3 |
Toko Cahaya Melati |
272 | ||
|
4 |
Toko Mawar Sari |
90 | ||
|
5 |
Coco Mart Ubud |
65 | ||
|
2 |
Depo Kapal |
6 |
CV Sumber Jaya |
100 |
|
7 |
Toko Sinar Wangi |
655 | ||
|
8 |
Toko Sol Mandala |
150 | ||
|
9 |
Toko Aris |
358 | ||
|
10 |
Toko Kayana |
25 | ||
|
3 |
Depo Mahend radatta |
6 |
CV Sumber Jaya |
1105 |
|
7 |
Toko Sinar Wangi |
50 | ||
|
8 |
Toko Sol Mandala |
300 | ||
|
9 |
Toko Aris |
99 | ||
|
10 |
Toko Kayana |
230 |
Tabel 5. Biaya Distribusi Per Dus
|
Sumber |
Tempat Tujuan |
Biaya per dus (Rp) | ||
|
Okt |
Nov |
Des | ||
|
Depo Klungk ung |
Toko Bintang |
50 |
0 |
0 |
|
Toko Subur |
30 |
20 |
30 | |
|
Toko Cahaya Melati |
75 |
80 |
90 | |
|
Toko Mawar Sari |
8800 |
8800 |
4400 | |
|
Coco Mart Ubud |
5000 |
10000 |
3750 | |
|
Depo Kapal |
CV Sumber Jaya |
55 |
0 |
0 |
|
Toko Sinar Wangi |
330 |
359 |
367 | |
|
Toko Sol Mandala |
1040 |
520 |
0 | |
|
Toko Aris |
263 |
280 |
292 | |
|
Toko Kayana |
1520 |
0 |
0 | |
|
Depo Mahend radatta |
CV Sumber Jaya |
553 |
350 |
467 |
|
Toko Sinar Wangi |
220 |
0 |
0 | |
|
Toko Sol Mandala |
600 |
600 |
600 | |
|
Toko Aris |
306 |
0 |
300 | |
|
Toko Kayana |
583 |
750 |
750 | |
Tabel 6. Biaya Rata-rata Distribusi Per Dus ( cU )
|
Sumber |
Tempat Tujuan |
Biaya Rata-rata per dus (Rp) |
|
Depo Klungkung |
Toko Bintang |
17 |
|
Toko Subur |
27 | |
|
Toko Cahaya Melati |
82 | |
|
Toko Mawar Sari |
7333 | |
|
Coco Mart Ubud |
6250 | |
|
Depo Kapal |
CV Sumber Jaya |
18 |
|
Toko Sinar Wangi |
352 | |
|
Toko Sol Mandala |
520 | |
|
Toko Aris |
278 | |
|
Toko Kayana |
507 | |
|
Depo Mahendra datta |
CV Sumber Jaya |
457 |
|
Toko Sinar Wangi |
73 | |
|
Toko Sol Mandala |
600 | |
|
Toko Aris |
202 | |
|
Toko Kayana |
694 |
Skema pendistribusian AMDK Club 600 ml dari masing-masing depo ke masing-masing tempat tujuan dapat dilihat pada Gambar 1.
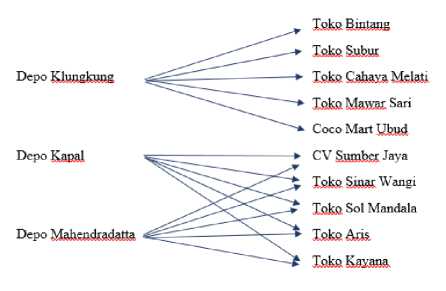
Gambar 1. Skema Pendistribusian AMDK 600 ml
Berdasarkan data pada Tabel 4 dan Tabel 6 diperoleh total biaya pendistribusian AMDK 600 ml di CV. Prasarana Fortuna Prima pada bulan Oktober–Desember 2018 sebelum dilakukan optimasi adalah sebesar Rp 2.393.186,00.
Formulasi Model Permasalahan Pendistribusian AMDK
Berdasarkan data penelitian yang telah dipaparkan pada Tabel 2 dan 3 dapat dilihat bahwa jumlah persediaan lebih besar dari jumlah permintaan, hal ini berarti model transportasi belum seimbang. Untuk membuat model transportasi yang seimbang, ditambahkan variabel dummy. Karena jumlah persediaan yang lebih besar dari jumlah
permintaan maka ditambahkan tujuan dummy untuk menyerap kelebihan tersebut dengan asumsi bahwa dummy memiliki biaya transportasi nol. Pada Gambar 1 dapat dilihat bahwa terdapat depo yang tidak mengirimkan AMDK ke suatu tempat tujuan sehingga diasumsikan biaya distribusinya sebesar M dengan M adalah bilangan positif yang sangat besar dan alokasi barang sebanyak 0 dus.
Pada formulasi model, variabel X1 (11) merupakan banyaknya AMDK yang dikirimkan dari depo Klungkung ke tujuan dummy, X2 (11) merupakan banyaknya AMDK yang dikirimkan dari depo Kapal ke tujuan dummy, dan X3 (11) merupakan banyaknya AMDK yang dikirimkan dari depo Mahendradatta ke tujuan dummy sehingga formulasi model permasalahan pendistribusian AMDK 600 ml adalah sebagai berikut:
Minimumkan
Z=17 ^ll +27%12 +82 ¾3 + 7333⅛
+ 6250%15 + Mx16 + Mx17
+ Mx18 + Mx19 + Mx1 (io) +0Xi (11)+Mx21 + Mx22 + Mx23 + Mx24 + Mx26 +18X26+352X27+520 *28 +278 ¾9 +507 *2 (10)
+0 *2 (11)+Mx31 + Mx32
+ Mx33 + Mx34 + Mx36
+457x36+73X37+600 *38 +202 ⅞9 +694 *3 (10)
+0 *3 (11)
dengan kendala
-
* 11 + *12 + *13 + *14 + *15 + *16 + *17 + *18 + *19 + *1 (10) + ^l (11) = 1293
-
* 21 + ⅞2 + ⅞3 + *24 + *25 + *26 + *27 + ¾8 + *29 + *2 (10) + *2 (11) = 4764
-
* 31 + *32 + *33 + *34 + *35 + *36 + *37 + *38 + *39 + *3 (10) + *3 (11) = 4218
-
* 11 + *21 + *31 =100
-
* 12 + *22 + *32 =450
-
* 13 + *23 + *33 =272
-
* 14 + *24 + *34 =90
-
* 15 + *25 + *35 =65
-
* 16 + *26 + *36 = 1205
-
* 17 + *27 + *37 =705
-
* 18 + *28 + *38 =450
-
* 19 + *29 + *39 =457
-
* 1 (10)+*2 (10)+*3 (10)=255
Xi (11)+*2 (11)+*3 (11) = 6226 xij≥0,i = 1,2,3 dan j=1,2,…,11 Berdasarkan asumsi sebelumnya bahwa dummy memiliki biaya transportasi 0 rupiah, depo yang tidak mengirimkan AMDK ke suatu tempat tujuan diasumsikan biaya distribusinya sebesar M dan alokasi barang sebanyak 0 dus sehingga formulasi model permasalahan pendistribusian AMDK 600 ml di atas menjadi: Minimumkan
Z=17Xn+27Xii +82 *13 + 7333*14
+ 6250^15 +18 ¾6 +352 ¾7 +520%28 +278 ¾9 +507 *2 (10)+457*36 +73 ¾7 +600 *38 +202 *39 +694 *3 (10)
dengan kendala
-
* 11 + *12 + *13 + *14 + *15 + *1 (11) = 1293
-
* 26 + *27 + *28 + *29 + *2 (10)+*2 (11) = 4764
-
* 36 + *37 + *38 + *39 + *3 (10)+*3 (11) = 4218
*11 =100
*12 =450
*13 =272
*14 =90
*15 =65
Perhitungan Solusi Awal
Sebelum dilakukan perhitungan solusi awal dengan RAM dan IVAM, terlebih dahulu dibentuk tabel awal transportasi. Berdasarkan data yang telah dikumpulkan, dimisalkan KL adalah depo Klungkung, KA adalah depo Kapal, MA adalah depo Mahendradatta dan TB adalah Toko Bintang, TS adalah Toko Subur, TC adalah Toko Cahaya Melati, TM adalah Toko Mawar Sari, CM adalah Coco Mart Ubud, SJ adalah CV. Sumber Jaya, SW adalah Toko Sinar Wangi, SM adalah Toko Sol Mandala, TA adalah Toko Aris, TK adalah Toko Kayana, D adalah dummy, Su adalah supply atau persediaan, dan De adalah demand atau permintaan. Berdasarkan formulasi model dapat dilihat bahwa *11 = 100, *12 = 450, *13 = 272, *14 =90, *15 =65 sehingga
-
* 1 (11)=1293-(100+450+272+90+ 65) = 316. Tabel awal transportasi dapat dilihat pada Tabel 7.
Perhitungan Russell’s Approximation Method (RAM)
Berdasarkan Tabel 7 dapat dihitung solusi awal menggunakan RAM dengan penyelesaian sebagai berikut:
Tabel 7. Tabel Awal Transportasi
|
Ke Dari |
TB |
TS |
TC |
TM |
CM |
SJ |
SW |
SM |
TA |
TK |
D |
Su |
|
KL |
17 100 |
27 450 |
82 272 |
7333 90 |
6250 65 |
M 0 |
M 0 |
M 0 |
M 0 |
M 0 |
0 316 |
1293 |
|
KA |
M 0 |
M 0 |
M 0 |
M 0 |
M 0 |
18 |
352 |
520 |
278 |
507 |
0 |
4764 |
|
MA |
M 0 |
M 0 |
M 0 |
M 0 |
M 0 |
457 |
73 |
600 |
202 |
694 |
0 |
4218 |
|
De |
100 |
450 |
272 |
90 |
65 |
1205 |
705 |
450 |
457 |
255 |
6226 |
10275 |
-
* 26 + *36 = 1205
-
* 27 + *37 =705
-
* 28 + *38 =450
-
* 29 + *39 =457
-
* 2 (10)+*3 (10)=255
*1 (11)+*2 (11)+*3 (11) = 6226 xij≥0,i = 1,2,3 dan j=1,2,…,11
-
1. Menentukan biaya distribusi tertinggi pada masing-masing baris ke-i ( ̅ l ) dan kolom ke- j ( ̅i). Pada Tabel 7 ̅2 = 520, dan ̅3 = 694. Sedangkan ̅6 = 457, ̅ =
352, ̅8 = 600, ̅9 = 278, ̅10 = 694, dan
̅11 =0
-
2. Perhitungan selisih biaya distribusi setiap sel adalah ∆^"26 = - ̅2- ̅ =18-
520-457=-959, dengan cara yang sama diperoleh ∆⅛7 = -520, ∆ =
-
-600, ∆ ⅛9 = -520, ∆ ¾(10) =-707,
∆ c2 (11) =-520, ∆c36 = -694, ∆ =
-
-973, ∆c38 = -694, ∆c39 = -770,
∆ c3 (10) = -694, ∆c3 (11) = -694.
-
3. Menentukan sel yang memiliki selisih biaya (∆ cij ) dengan negatif terbesar. Pada langkah 2, nilai selisih biaya (∆C^ ) dengan negatif terbesar adalah ∆C37. Kemudian alokasikan produk ke sel yang berada pada baris 3 kolom 7 sebanyak 705 (min (4218,705) = 705).
Berdasarkan pengalokasian tersebut kolom 7 telah terpenuhi sehingga kolom 7 tidak digunakan lagi untuk menentukan biaya distribusi tertinggi berikutnya. Setelah diulangi langkah 1 sampai langkah 3 diperoleh hasil akhir pengalokasian AMDK 600 ml menggunakan RAM pada iterasi ke-6 yang dapat dilihat pada Tabel 8 dengan total biaya distribusi sebesar Rp 1.631.128,00.
Perhitungan Improved Vogel’s Approximation Method (IVAM)
Berdasarkan Tabel 7 dapat dihitung solusi awal menggunakan IVAM dengan penyelesaian sebagai berikut:
-
1. Menghitung nilai Total Opportunity Cost (TOC). Terlebih dahulu dicari Row
Opportunity Cost. Pada Tabel 7 biaya distribusi terendah pada baris 2 adalah 0 dan baris 3 adalah 0 sehingga kurangkan setiap biaya distribusi pada masing-masing baris dengan biaya distribusi terendah pada baris yang sama. Contoh perhitungan: biaya distribusi pada baris 2 kolom 6 adalah 18 dan biaya distribusi terendah pada baris 2 adalah 0 sehingga nilai Row Opportunity Cost pada baris 2 kolom 6 adalah 18 – 0 = 18. Selanjutnya dicari Column Opportunity Cost. Pada Tabel 7 biaya distribusi terendah pada kolom 6 adalah 18, kolom 7 adalah 73, kolom 8 adalah 520, kolom 9 adalah 202, kolom 10 adalah 507, dan kolom 11 adalah 0 sehingga kurangkan setiap biaya distribusi pada masing-masing kolom dengan biaya distribusi terendah pada kolom yang sama. Contoh perhitungan: biaya distribusi pada baris 2 kolom 6 adalah 18 dan biaya distribusi terendah pada kolom 6 adalah 18 sehingga nilai Column Opportunity Cost
pada baris 2 kolom 6 adalah 18 – 18 = 0. Kemudian hasil Row Opportunity Cost dan Column Opportunity Cost dijumlahkan sehingga diperoleh nilai TOC seperti berikut: baris 2 kolom 6 = 18, baris 2 kolom 7 = 631, baris 2 kolom 8 = 520, baris 2 kolom 9 = 354, baris 2 kolom 10 = 507, baris 2 kolom 11 = 0, baris 3 kolom 6 = 896, baris 3 kolom 7 = 73, baris 3 kolom 8 = 680, baris 3 kolom 9 = 202, baris 3 kolom 10 = 881, baris 3 kolom 11 = 0.
-
2. Mencari selisih biaya terendah dengan biaya terendah berikutnya untuk setiap baris dan kolom yang sama. Biaya yang digunakan adalah biaya yang telah diperoleh pada langkah 1 (TOC). Berikut adalah selisih dua biaya terendah pada masing-masing baris dan kolom: baris 2 = 18, baris 3 = 73, kolom 6 = 878, kolom 7 = 558, kolom 8 = 160, kolom 9 = 152, kolom 10 = 374, kolom 11 = 0.
-
3. Memilih tiga selisih biaya dengan nilai yang terbesar (jika terdapat nilai yang sama maka dapat dipilih secara sembarang). Hasil perhitungan selisih dua biaya terendah pada langkah 2 dapat dilihat bahwa selisih biaya terbesar yang pertama adalah 878 sehingga terlebih dahulu dialokasikan produk ke sel yang memiliki biaya terendah pada kolom 6. Biaya terendah pada kolom 6 adalah 18 sehingga alokasikan produk pada sel tersebut sebanyak 1205 (min (4764,1205) = 1205). Selanjutnya selisih biaya terbesar adalah 558 sehingga alokasikan produk ke sel yang memiliki biaya terendah pada kolom 7. Biaya terendah pada kolom 7 adalah 73 sehingga alokasikan produk pada sel tersebut sebanyak 705 (min (4218,705) = 705). Kemudian selisih biaya terbesar adalah 374 sehingga alokasikan produk ke sel yang memiliki biaya terendah pada kolom 10. Biaya terendah pada kolom 10 adalah 507 sehingga alokasikan produk pada sel tersebut sebanyak 255 (min (3559,255) = 255).
Berdasarkan pengalokasian tersebut, kolom 6, kolom 7, dan kolom 10 telah terpenuhi sehingga kolom 6, kolom 7, dan kolom 10 tidak digunakan lagi untuk menghitung selisih dua biaya terendah berikutnya. Setelah diulangi langkah 2 sampai langkah 3 diperoleh hasil akhir pengalokasian AMDK 600 ml menggunakan IVAM pada iterasi ke-3 yang dapat dilihat pada Tabel 9 dengan total biaya distribusi sebesar Rp 1.667.128,00.
Tabel 8. Hasil Akhir Pengalokasian dengan RAM
|
Ke Dari |
TB |
TS |
TC |
TM |
CM |
SJ |
SW |
SM |
TA |
TK |
D |
Su |
|
KL |
17 100 |
27 450 |
82 272 |
7333 90 |
6250 65 |
M |
M |
M |
M |
M |
0 316 |
1293 |
|
KA |
M |
M |
M |
M |
M |
18 1205 |
352 |
520 450 |
278 |
507 255 |
0 2854 |
4764 |
|
MA |
M |
M |
M |
M |
M |
457 |
73 705 |
600 |
202 457 |
694 |
0 3056 |
4218 |
|
De |
100 |
450 |
272 |
90 |
65 |
1205 |
705 |
450 |
457 |
255 |
6226 |
10275 |
Tabel 9. Hasil Akhir Pengalokasian dengan IVAM
|
Ke Dari |
TB |
TS |
TC |
TM |
CM |
SJ |
SW |
SM |
TA |
TK |
D |
Su |
|
KL |
17 100 |
27 450 |
82 272 |
7333 90 |
6250 65 |
M |
M |
M |
M |
M |
0 316 |
1293 |
|
KA |
M |
M |
M |
M |
M |
18 1205 |
352 |
520 |
278 |
507 255 |
0 3304 |
4764 |
|
MA |
M |
M |
M |
M |
M |
457 |
73 705 |
600 450 |
202 457 |
694 |
0 2606 |
4218 |
|
De |
100 |
450 |
272 |
90 |
65 |
1205 |
705 |
450 |
457 |
255 |
6226 |
10275 |
Perhitungan Solusi Optimal (Uji Optimalitas)
Perhitungan RAM menghasilkan solusi awal seperti pada Tabel 8. Selanjutnya dilakukan uji optimalitas menggunakan MODI. Terlebih dahulu dipastikan jumlah sel dengan variabel dasar sama dengan m+n-1. Pada Tabel 8 dapat dilihat bahwa m=3, n=11, dan jumlah sel dengan variabel dasar adalah 13 sehingga jumlah sel dengan variabel dasar yang diperoleh saat pemecahan awal sama dengan m+n-1. Kemudian berdasarkan Tabel 8 dihitung nilai indeks baris dan kolom dengan menetapkan U1=0, diperoleh nilai indeks pada masing-masing baris dan kolom sebagai berikut: U2 =0, U2 =0, vι=17, V2 =27, V3 =82, V4 = 7333, vS = 6250, V6=18, V7 =73, V8 = 520, V9 = 202, vW = 507, vH =0. Setelah diperoleh nilai indeks, dilanjutkan dengan menghitung besarnya nilai opportunity cost. Contoh perhitungan: ̅̅̅̅ =
C16 - U1 - V6 = -0-18=M-18,
dengan cara yang sama diperoleh ̅̅̅̅ = M-73, ̅̅̅̅ = M - 600, ̅̅̅̅ = M - 202, ̅̅̅(̅̅̅̅) = M-507, ̅̅̅̅ =M-17, ̅̅̅̅ =M(-)27,
̅̅̅̅ = M-82, ̅̅̅̅ =M - 7333, ̅̅̅̅ = M-
6250, ̅̅̅̅=279, ̅̅̅̅=76, ̅̅̅̅=M-17,
̅̅̅̅ = M-27, ̅̅̅̅ =M-82, ̅̅̅̅ =M-
7333, ̅̅̅̅ = M-6250, ̅̅̅̅=439, ̅̅̅̅=0, ̅̅̅(̅̅̅̅) = 187. Berdasarkan perhitungan, nilai pada sel-sel yang kosong (opportunity cost) tidak ada yang bernilai negatif sehingga Tabel 8 telah optimal.
Perhitungan IVAM menghasilkan solusi awal seperti pada Tabel 9. Selanjutnya dilakukan uji optimalitas menggunakan MODI. Terlebih dahulu dipastikan jumlah sel dengan variabel dasar sama dengan m+n-1. Pada Tabel 9 dapat dilihat bahwa m=3, n=11, dan jumlah sel dengan variabel dasar adalah 13 sehingga jumlah sel dengan variabel dasar yang diperoleh saat pemecahan awal sama dengan
m+n-1. Kemudian berdasarkan Tabel 9 dihitung nilai indeks baris dan kolom dengan menetapkan U1=0, diperoleh nilai indeks pada masing-masing baris dan kolom sebagai berikut: U2 =0, u3 =0, Ul=17, V2 =27, U3 =82, U4 = 7333, U5 = 6250, ⅝ =18, U7 =73, U8 = 600, U9 = 202, UlO = 507,
Ull =0. Setelah diperoleh nilai indeks, dilanjutkan dengan menghitung besarnya nilai opportunity cost. Contoh perhitungan: ̅̅̅̅ = C16 - U1 - U6 = -0-18=M-18,
dengan cara yang sama diperoleh ̅̅̅̅ = M-73, ̅̅̅̅ = M - 600, ̅̅̅̅ = M - 202, ̅̅̅(̅̅̅̅) = M - 507, ̅̅̅̅ = M-17, ̅̅̅̅ =M-27,
̅̅̅̅ = M-82, ̅̅̅̅ =M - 7333, ̅̅̅̅ = M-6250, ̅̅̅̅ = 279, ̅̅̅̅ = -80, ̅̅̅̅ = 76,
̅̅̅̅ = M - 1=7, ̅7̅̅9̅, = M =--2870, , ̅̅̅̅ = 2M =-7862,, ̅̅̅̅ = M - 7333, ̅̅̅̅ = M - 6250, ̅̅̅̅ =
439, ̅̅̅(̅̅̅̅) = 187. Berdasarkan perhitungan terdapat sel kosong yang bernilai negatif maka dilanjutkan dengan memilih variabel masuk dengan memilih nilai ̅̅̅ yang paling negatif yaitu ̅̅̅̅ sehingga X2 8 dipilih sebagai variabel masuk. Setelah memilih variabel masuk dilanjutkan dengan menentukan variabel keluar menggunakan jalur tertutup dengan memberi tanda positif pada sel baris 2 kolom 8, kemudian memberi tanda negatif pada sel baris 2 kolom 11, memberi tanda positif pada sel baris 3 kolom 11, dan memberi tanda negatif pada sel baris 3 kolom 8. Pada jalur tertutup, isi sel yang bertanda negatif yang memiliki nilai terkecil adalah 450 (min (3304,450) = 450) sehingga ⅞8 dipilih sebagai variabel keluar. Selanjutnya tambahkan X28 sebanyak 450, kurangkan X2 (11) sebanyak 450, tambahkan ⅞(11) sebanyak 450, dan kurangkan ⅞8 sebanyak 450. Diperoleh hasil iterasi 1 sama seperti hasil akhir pengalokasian dengan RAM maka telah diperoleh solusi optimal.
Dengan demikian total biaya distribusi AMDK 600 ml dari bulan Oktober–Desember 2018 yang optimal adalah sebesar Rp 1.631.128,00 dengan rute pengiriman yaitu dari depo Klungkung ke Toko Bintang, Toko Subur, Toko Cahaya Melati, Toko Mawar Sari, dan Coco Mart Ubud, dari depo Kapal ke CV. Sumber Jaya, Toko Sol Mandala, dan Toko Kayana, dari depo Mahendradatta ke Toko Sinar Wangi dan Toko Aris. Pada penelitian ini terjadi penurunan biaya sebesar Rp 762.058,00 atau 32% dari total biaya distribusi yang dikeluarkan oleh CV. Prasarana Fortuna Prima sebelum dilakukan optimasi. Perlu diingat
bahwa dalam penelitian ini biaya distribusi yang digunakan hanya biaya BBM, untuk biaya yang lainnya tidak diperhitungkan sehingga apabila ada biaya yang lain maka perlu dilakukan perhitungan lagi.
Berdasarkan hasil penelitian diperoleh bahwa RAM menghasilkan solusi awal yang lebih minimum dari IVAM, akan tetapi RAM memerlukan iterasi yang lebih banyak dari IVAM. Berdasarkan hasil uji optimalitas menggunakan MODI, solusi awal yang diperoleh dari RAM sudah optimal sedangkan solusi awal yang diperoleh dari IVAM memerlukan 1 iterasi untuk memperoleh solusi optimal. Rute pendistribusian yang diperoleh yaitu dari depo Klungkung ke Toko Bintang, Toko Subur, Toko Cahaya Melati, Toko Mawar Sari, dan Coco Mart Ubud, dari depo Kapal ke CV. Sumber Jaya, Toko Sol Mandala, dan Toko Kayana, dari depo Mahendradatta ke Toko Sinar Wangi dan Toko Aris dengan total biaya distribusi yang lebih minimum dari sebelum dilakukan optimasi.
Pada penelitian ini data biaya distribusi yang digunakan hanya biaya BBM tetapi pada kenyataannya terdapat biaya lain yang dikeluarkan seperti biaya sopir dan biaya perbaikan kendaraan sehingga untuk penelitian selanjutnya diharapkan menambahkan data biaya tersebut. Selain itu, pada permasalahan transportasi terdapat suatu kasus di mana saat pendistribusian, barang yang diangkut dari sumber tidak langsung dikirim ke tempat tujuan tetapi melalui tempat transit sehingga untuk menyelesaikan permasalahan tersebut dapat digunakan model transshipment.
DAFTAR PUSTAKA
Hasibuan, N. A. (2017). Russell Approximation Method and Vogel's Approximation Method in Solving Transport Problem. International Journal of Informatics and Computer Science (The IJICS), 1 No. 1, 17.
Hillier, F. S., & Lieberman, G. J. (1994). Introduction to Operation Research (7th ed.). New York: McGraw-Hill.
Korukoğlu, S., & Ballı, S. (2011). An Improved Vogel's Approximation Method for The Transportation Problem. Mathematical and Computational Applications, 16
Nomor 2, 370-381.
Nahar, J., Rusyaman, E., & Putri, S. (2018). Application of Improved Vogel's Approximation Method in Minimization of Rice Distribution Costs of Perum BULOG. IOP Conference Series: Materials Science and Engineering, 332 Nomor 1, 1-8.
Nofrianto, A. (2015). Model Transportasi Pengaturan Pasokan Pendistribusian Air PDAM Kota Padang untuk
Meminimalisasi Biaya Produksi (Studi Kasus Metode Aproksimasi Vogel dan Metode Aproksimasi Russell). Retrieved September 11, 2018, from
http://repository.unp.ac.id/7797/
Sari, D. P. (2014). Optimasi Distribusi Gula Merah pada UD Bumi Sari Raya Menggunakan Model Transportasi dan Metode Least Cost. Sistem Informasi, 3 Nomor 2, 1-9.
Siswanto. (2007). Operation Research Jilid I. (T. Prasetyo, & Y. Sumiharti, Eds.) Jakarta: Penerbit Erlangga.
193
Discussion and feedback