ANALISIS HUBUNGAN PRODUKSI PERIKANAN TANGKAP LAUT, CURAH HUJAN, DAN SUHU PERMUKAAN LAUT DENGAN MODEL VECTOR AUTOREGRESSIVE (VAR)
on
E-Jurnal Matematika Vol. 8(2), Mei 2019, pp.155-163
DOI: https://doi.org/10.24843/MTK.2019.v08.i02.p247
ISSN: 2303-1751
ANALISIS HUBUNGAN PRODUKSI PERIKANAN TANGKAP LAUT, CURAH HUJAN, DAN SUHU PERMUKAAN LAUT
DENGAN MODEL VECTOR AUTOREGRESSIVE (VAR)
Ramadhan Lenggu Ramli1§, I Wayan Sumarjaya 2, Kartika Sari 3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: ramadhanramli88@gmail.com]
-
2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@gmail.com]
-
3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: sarikaartika@unud.ac.id]
§Corresponding Author
ABSTRACT
NTT Province is one of the provinces with the largest marine catch fisheries production in Indonesia. Rainfall and sea surface temperature are factors that affect marine catch fisheries production. This study aims to analyze relationships between marine catch fisheries production, sea surface temperature and rainfall in NTT based on time series data using a vector autoregressive model (VAR). The result of this study: (i) the best VAR model for forecasting marine catch fisheries, rainfall, and sea surface temperature is a second-order VAR model (VAR (2)), (ii) based on MAPE forecasting criterion, the VAR model obtained classified as good forecasting for variable production of marine catch fisheries, and sea surface temperature, while for rainfall forecasting is inaccurate, (iii) significant sea surface temperatures affect marine catch fisheries production and rainfall in NTT.
Keywords: Forecasting, MAPE, Marine catch fisheries production, Vector autoregressive (VAR).
Metode peramalan merupakan seni dan ilmu memprediksi peristiwa-peristiwa masa depan dengan pengambilan data historis dan memproyeksikannya ke masa depan menggunakan model matematis (Heizer et al., 2011). Metode peramalan dapat digunakan untuk meramalkan produksi perikanan tangkap laut. Peramalan produksi perikanan tangkap laut dapat dipakai sebagai acuan bagi pemerintah dalam mengoptimalkan ekspor ikan.
Indonesia merupakan sebuah negara yang memiliki produksi perikanan tangkap laut melimpah. Menurut BPS (2018) jumlah penangkapan ikan laut di Indonesia tahun 2015 sebanyak 6.204.668 ton, pada tahun 2016 sebanyak 6.334.106 ton, dan pada tahun 2017 sebanyak 6.570.056 ton. Salah satu Provinsi dengan produksi perikanan tangkap yang banyak adalah Provinsi Nusa Tenggara Timur. Menurut BPS (2018) jumlah penangkapan ikan laut di Provinsi NTT pada tahun 2015 sebanyak 118.389 ton, pada tahun 2016 sebanyak 123.766
ton, dan pada tahun 2017 sebanyak 138.268 ton, berdasarkan data tersebut terlihat adanya peningkatan jumlah penangkapan ikan di Provinsi NTT dari tahun 2015 sampai tahun 2017.
Produksi perikanan tangkap tidak terlepas dari sebaran kelimpahan ikan. Sebaran kelimpahan ikan dipengaruhi oleh dinamika oseanografi. Beberapa parameter dinamika oseanografi antara lain suhu air laut, arus laut, salinitas, dan ketersediaan makanan. Suhu merupakan parameter oseanografi yang berpengaruh sangat dominan terhadap kehidupan ikan. Setiap jenis ikan mempunyai suhu optimum untuk kehidupannya (Lalli and Parsons, 1997). Selain suhu, salinitas berpengaruh terhadap berlangsungnya proses biologis yang secara langsung memengaruhi laju pertumbuhan, jumlah makanan yang dikonsumsi, nilai konversi makanan, dan daya kelangsungan hidup ikan (Robinson, 2010).
Metode analisis yang dapat digunakan untuk
meramalkan adalah analisis deret waktu. VAR merupakan metode deret waktu yang dapat digunakan untuk memodelkan dan meramalkan lebih dari satu variabel secara simultan. Keunggulan dari metode VAR adalah (1) bentuk model sederhana tidak perlu menentukan variabel endogen dan variabel eksogen karena dalam model ini, semua variabel adalah variabel endogen; (2) estimasi model VAR bersifat sederhana yaitu bisa menggunakan metode kuadrat terkecil (MKT); (3) hasil peramalan yang diperoleh dari metode ini lebih baik dibandingkan dengan model simultan kompleks lainnya (Gujarati, 2004).
Penelitian terkait metode VAR telah dilakukan oleh Ranangga, et al. (2018) menunjukkan bahwa nilai MAPE pada model VAR (6) memberikan peramalan yang baik dalam meramalkan jumlah kunjungan wisatawan Cina (15,9%) dan memberikan hasil peramalan yang akurat dalam meramalkan jumlah kunjungan wisatawan Australia (6,8%) dan Jepang (9%). Sementara itu, penelitian peramalan produksi penangkapan ikan telah dilakukan oleh Bako et al. (2013) dengan menggunakan model ARIMA. Dari penelitian Bako et al. (2013), diperoleh model ARIMA (1,1,0) (0,0,1)12 dan model SARIMA (0,1,1) (0,0,1)12 sebagai model terbaik dalam meramalkan jumlah penangkapan ikan selayor dan ikan tambun beluru di perairan Malaysia. Sedangkan penelitian pengaruh oseanografi terhadap perikanan tangkap laut telah dilakukan oleh Perdana dan Susilowati (2015) dengan menggunakan metode pendekatan kualitatif secara deskriptif, memberikan hasil bahwa gejala-gejala perubahan iklim yang dirasakan oleh masyarakat nelayan di Kota Semarang yaitu, curah hujan dengan intensitas tinggi, angin kencang, dan gelombang tinggi, berdampak pada adanya perubahan volume hasil tangkapan yang mengakibatkan penurunan pendapatan nelayan dan perubahan biaya melaut.
Berdasarkan uraian di atas, mengingat bahwa produksi perikanan tangkap laut antara lain dipengaruhi oleh curah hujan dan suhu permukaan laut sementara dilain pihak Provinsi
NTT merupakan salah satu provinsi dengan produksi perikanan tangkap yang banyak, maka penulis tertarik melakukan penelitian mengenai hubungan produksi perikanan tangkap laut, curah hujan, dan suhu permukaan laut di Provinsi NTT dengan menggunakan model VAR.
-
2. TINJAUAN PUSTAKA
-
a. Vector Autoregressive (VAR)
Dalam model ini semua variabel dianggap sebagai variabel endogen. Bentuk umum model VAR orde p (VAR (p)), untuk K variabel deret waktu adalah sebagai berikut (Lütkepohl, 2005): yt = + AιYt-ι + A2Yt-2 +⋯+ApYt-P +
ut , untuk t = 0, ±1, ±2,… (1)
dengan Yt=(Vit, Y2t, Y3t,…,Yκt ) ' adalah
vektor berukuran K, Ai adalah matriks
parameter variabel endogen berukuran (K×K) untuk i = 1,2,․․․,P, v=( ^l , V2 , V3,…,vK ) ' adalah vektor yang berisi konstanta berukuran K, dan ut=( ^,lt , ^2t , ^3t ,…, ^Kt ) ' adalah galat model. Vektor Ut diasumsikan sebagai proses white noise yaitu suatu proses stokastik yang saling bebas dengan rata-rata 0 dan timeinvariant.
-
b. Identifikasi Model
Identifikasi orde VAR merupakan tahap untuk menentukan model VAR yang cocok. Diasumsikan bahwa M merupakan batas atas dari orde model VAR, urutan hipotesis yang diuji adalah:
Ho ∶ = 0 vs Hl ∶ ≠0 |Am =0
Hipotesis diuji secara berurutan dari Hq dan proses berhenti sampai menemukan hipotesis nol yang ditolak. Hal ini berarti, jika Hq ditolak, maka ̂ = M-i + 1 akan terpilih sebagai estimasi orde dari model VAR. Uji statistik yang digunakan untuk menguji Hq adalah uji likelihood ratio (LR) yang dirumuskan sebagai (Lütkepohl, 2005):
^LR (i)=T[ln| ̃U(M-i)|-ln| ̃U(M-i+1)|] (2)
dengan ̃ u(m) merupakan penduga MLE dari ∑u ketika model VAR(m) cocok untuk deret waktu dengan panjang T. Uji likelihood ratio (LR) secara asymptotic berdistribusi Chi-square dengan derajat bebas K2 , yaitu Z2 (K2). Pada pengujian ini, jika ^LR (i)> Xk2 ;a atau P- value <a , maka Hq ditolak.
Selain menggunakan uji LR untuk menentukan orde model VAR terdapat beberapa kriteria untuk memilih orde model VAR yaitu final prediction error (FPE), Akaike’s Information Criterion (AIC), Hannan-Quinn Criterion (HQ), dan Schwarz Information Criterion (SC) yang secara berturut-turut dirumuskan sebagai :
dengan T adalah ukuran sampel, K adalah banyak variabel, dan ̃ U(m) merupakan nilai duga MLE dari Xr. Estimasi orde ( ̂) model yang dipilih adalah ̂=m sedemikian sehingga nilai kriteria FPE(m), AIC (m), HQ(m), atau SC(m) yang dihasilkan adalah yang terkecil, dengan m=0,1,2,…,M (Lü tkepohl, 2005).
-
c. Diagnostik Model
Uji portmanteau digunakan untuk menguji autokorelasi dari residual model. Hipotesis yang diuji adalah
Hq ∶ = =⋯= =0, (tidak terdapat
autokorelasi pada residual model dari beda kala 1 sampai h),
Hy ∶ paling sedikit ada satu Ri≠0, dengan
i=1,2,3,․․․,ℎ. (terdapat paling sedikit satu autokorelasi pada residual model).
Uji statistik untuk mengecek hipotesis ini adalah:
Qh = ∑ ^-ι tr( ̂;̂ ̂îr ) (7)
dengan ̂j =∑t=i+ι ̂ ̂ dan ̂■ f merupakan residual dari model VAR(p) yang stabil. Uji portmanteau secara asymptotic berdistribusi Chi-square dengan derajat bebas K2(ℎ-P).
Kriteria uji portmanteau: Hq ditolak apabila Qh > Xk2 (h-p);a atau P- value <a (Lütkepohl and Kratzig, 2004).
Selanjutnya uji kenormalan dilakukan untuk mengetahui apakah residual dari model VAR menyebar normal. Uji kenormalan yang digunakan pada deret waktu berganda untuk menguji kenormalan residual model adalah uji Lomnicki-Jarque-Bera (LJB). Hipotesisnya adalah
Hq ∶ residual model menyebar normal, Hy ∶ residual model tidak menyebar normal. Statistik uji Lomnicki-Jarque-Bera (LJB) adalah: LJBk = + sj , (8)
dengan sI atau skewness adalah derajat
ketidaksimetrisan suatu distribusi data dan S4 atau kurtosis adalah ukuran ekor suatu distribusi
data. Skewness dan kurtosis dirumuskan sebagai:
_ ⅛
= dan
3 6
c,2 _ T(v⅛) ' (v⅛)
S4 =
dengan
bi=(b n, ⅛12 , ⅛13 ,…,L,ικ)′ dengan
T∑M( ̂ Skt)3,k=1,2,3,…,K
⅛2 =(L>2l, L 22, L>23,…,t>2K)′ dengan
T∑Ll( ̂ kt)4,k=1,2,3,…,K
3κ=(3,3,3,…,3)′ berukuran (K×1),
(9)
(10)
=
=
LJB secara asymptotic berdistribusi Chisquare dengan derajat bebas 2K. Kriteria uji LJB : Hq ditolak apabila, LJBk > X2K;a atau P- value <a (Lütkepohl and Kratzig, 2004).
-
d. Kriteria MAPE
Kemampuan model dalam melakukan peramalan bisa dilihat dari hasil perhitungan ketepatan peramalan. Salah satu ukuran statistik yang bisa digunakan untuk mengukur ketepatan peramalan adalah mean absolute percentage error (MAPE). Nilai MAPE dirumuskan sebagai (Lütkepohl and Kratzig, 2004):
MAPE = ∑ Li | ^ ̅ t-|×100% (11) a l l yt
dengan a merupakan banyak data, ̅ f merupakan hasil peramalan, dan yt merupakan nilai yang sesungguhnya dari variabel yang diprediksi. Kriteria peramalan MAPE dapat dilihat dalam Tabel 1.
Tabel 1. Kriteria Nilai MAPE
|
MAPE |
Kekuatan Peramalan |
|
< 10% |
Peramalan sangat akurat |
|
10 %– 20% |
Peramalan baik |
|
20% – 50% |
Peramalan masuk akal (wajar) |
|
> 50% |
Peramalan tidak akurat |
Sumber : Zhang et al. (2015)
Uji kausalitas granger sangat populer dalam beberapa tahun terakhir, idenya adalah efek atau akibat tidak dapat terjadi sebelum adanya penyebab. Variabel xt memengaruhi variabel zt, jika informasi terdahulu dan saat ini dari variabel xt dapat membantu memprediksi informasi variabel zt (Lutkepohl, 2005).
Misalkan diberikan VAR (p) dengan dua peubah x t dan zt sebagai berikut : (Xt) = GWXiw KiwIGt-Wt) (12)
VW2 ' l iL u 2 i, l K 2 2,1-I∖zt- i' V uZt'
Hipotesis untuk uji kausalitas granger adalah H0: α2i, j = 0 untuk i= 1,2, ...,p (X tidak
granger cause Y)
Hi: ¾i, j≠0 untuk i= 1,2, .,p (X granger
cause )
Statistik uji yang digunakan adalah
F =
p-⅛j
'“M , Lτ-(o +q- 1)J
(13)
dengan RSSr adalah jumlah kuadrat residual dari model terestriksi, SSSu adalah jumlah kuadrat residual dari model yang tidak terestriksi, o adalah jumlah lag pada model terestriksi dan q adalah jumlah lag pada model yang tidak terestriksi. Kriteria uji : H0 ditolak jika nilai F > nilai kritis F (Luitkepohl and Kratzig, 2004).
-
f. Impuls Response Function
Impulse response function (IRF) digunakan karena, kausalitas granger tidak memberi informasi lengkap tentang interaksi antarvariabel. Pengaruh guncangan (shock) pada salah satu variabel terhadap beberapa variabel dalam VAR dapat diketahui dengan
menggunakan impulse response function. IRF menelusuri respon dari variabel dependen dalam system VAR terhadap guncangan (shock) dalam error ( ) dan mengamati dampak dari
guncangan tersebut untuk beberapa periode ke depan. Dengan melakukan plot IRF secara visual dapat diamati perilaku satu variabel dalam menerima berbagai guncangan (shock) dari variabel lain dalam sistem (Enders, 2015).
Data yang digunakan pada penelitian ini adalah data sekunder yaitu data produksi perikanan tangkap laut, curah hujan dan suhu permukaan laut di Provinsi NTT yang diperoleh dari Dinas Kelautan dan Perikanan Provinsi NTT dan BMKG Provinsi NTT. Data yang digunakan adalah data bulanan dari bulan Juli 2012 sampai bulan Desember 2017. Data dari bulan Juli 2012 sampai bulan Februari 2017 akan digunakan dalam pembentukan model dan data dari bulan Maret 2017 sampai bulan Desember 2017 akan digunakan untuk menghitung nilai MAPE. Data curah hujan dan suhu permukaan laut yang digunakan dalam penelitian ini merupakan rerata data dari lima titik wilayah di Provinsi NTT, yaitu Laut Flores, Laut Sawu, Selat Ombai, Selat Sumba, dan Samudera Indonesia.
Penelitian ini menggunakan tiga variabel deret waktu dengan ketiga variabel tersebut menjadi variabel endogen. Variabel-variabel yang diteliti yaitu produksi perikanan tangkap laut, curah hujan, dan suhu permukaan laut di Provinsi NTT. Adapun tahapan penyesaian
dalam penelitian ini yaitu:
-
1. melakukan analisis deskriptif;
-
2. melakukan pemilihan orde model VAR;
-
3. melakukan estimasi parameter model;
-
4. uji portmanteau;
-
5. uji Lomnicki-Jarque-Bera (LJB);
-
6. uji kestabilan model;
-
7. menghitung nilai MAPE;
-
8. melakukan peramalan;
-
9. pengkajian kausalitas granger;
-
10. pengkajian fungsi respon impuls.
Berdasarkan Gambar 1, Gambar 2, dan Gambar 3 dapat dilihat bahwa terdapat musiman pada data produksi perikanan laut, suhu permukaan laut, dan curah hujan di NTT.
Produksi Perikanan Tangkap Laut di NTT
b. Identifikasi Model
Identifikasi model dilakukan dengan terlebih dahulu menentukan orde optimum dari model dengan menggunakan data produksi perikanan tangkap laut, suhu permukaan laut dan curah hujan di NTT pada Juli 2012 sampai Februari 2017. Nilai uji LR, AIC, HQ, FPE, dan SC dapat dilihat pada Tabel 2 berikut.
14000
12000
10000
8000
6000
4000
2000 0


Gambar 1. Plot Data Produksi Perikanan Tangkap Laut di NTT bln Juli 2012-Februari 2017
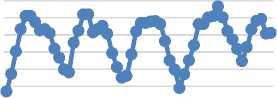
Suhu Permukaan Laut di NTT
32.000
31.000
30.000
29.000
28.000
27.000
26.000
25.000
24.000
23.000
Mcnm^-,ςtL∩L∩kDΦΓ×
Gambar 2. Plot Data Suhu Permukaan Laut di NTT Bulan Juli 2012-Februari 2017
700
600
500
400
300
200
100
0
Curah Hujan di NTT

Gambar 3. Plot Data Curah Hujan di NTT Bulan Juli 2012-Februari 2017
Tabel 2. Nilai Kriteria Pemilihan Orde
Lag
LR
FPE
AIC
SC
HQ
0
NA
5,7 × 10 1 0
33,3
33,4
33,3
1
143,5
4,9 × 109
30,8
31,3
31,0
2
52,1
2,3 × 109
30,1
30,8
30,4
3
22,7
2,0 × 109
29,9
31,0
30,3
4
32,2
1,3 × 1O9
29,5
30,9
30,0
5
11,9
1,4 × 109
29,5
31,2
30,2
6
13,1
1,4 × 109
29,5
31,5
30,3
7
11,8
1,4 × 109
29,5
31,8
30,4
8
11,8
1,4 × 109
29,4
32,1
30,4
Orde optimum yang terpilih berdasarkan masing-masing kriteria dapat dilihat pada Tabel 2 dengan nilai dalam sel yang dicetak tebal. Dapat dilihat bahwa orde dua terpilih berdasarkan kriteria uji SC, orde empat terpilih berdasarkan kriteria uji LR, FPE dan HQ, serta orde delapan terpilih berdasarkan kriteria uji AIC. Orde delapan tidak dipilih karena banyak mengambil data untuk pembentukan model. Orde empat juga tidak dipilih karena setelah dilakukan uji normalitas yang merupakan salah satu asumsi yang harus dipenuhi untuk membentuk model VAR tidak terpenuhi. Oleh karena itu, orde model VAR dari data produksi perikanan tangkap laut, suhu permukaan laut dan curah hujan di NTT yang dipilih adalah dua.
Selanjutnya, model produksi perikanan tangkap laut, suhu permukaan laut, dan curah hujan secara berturut-turut disimbolkan dengan L, S, dan H. Setelah orde model dipilih, langkah selanjutnya adalah estimasi parameter.
c. Estimasi Parameter
Estimasi parameter model menggunakan metode multivariate least square (MLS). Berdasarkan pembahasan terdahulu diperoleh
orde model L, S, dan H di NTT adalah dua. Estimasi model VAR dapat dilihat pada persamaan (14).
Lt 18173,68
St = 11,22727 + X1
H -11,17,064
dengan
∣‰-ι Lt-21
[St-1]+^2 [St-2 ] (14)
Ht-1 H
0,992068 -238,1576 0,774217
X1 = [8,749 × 10^≡ 1,263339 0,002216
-0,022688 58,18294 0,7001698
dan
2
-0,146694 -364,6648 3,678113
[-4,929 × 10“S -0,672192 -0,001027
0,0114401 -12,44571 -0,3630004
Uji autokorelasi antarresidual model VAR pada persamaan (14) yang digunakan adalah uji portmanteau. Data yang digunakan untuk memperoleh model VAR pada persamaan (14) berjumlah 56 data yaitu dari Juli 2012 sampai Februari 2017 dengan orde optimum yang dipilih adalah dua. Hal ini berarti beda kala (lag) autokorelasi antarresidual terbesar yang dapat terbentuk adalah 54.
Diperoleh nilai ^54 = 291,6690 dengan nilai p-value = 1,0000 yang dapat dilihat pada Tabel 3. Penarikan keputusan menggunakan tingkat signifikan 5%. Karena nilai p-value dari Q54 lebih besar dari 5%, maka tidak cukup bukti untuk menolak Hq . Dengan kata lain, tidak terdapat autokorelasi antarresidual estimasi model VAR pada persamaan (14).
Tabel 3. Nilai Statistik Uji Portmanteau
|
Lags |
Q-Stat |
Prob.* |
|
1 |
10.57222 |
--- |
|
2 |
17.08798 |
--- |
|
3 . |
20.95615 . |
0.0128 . |
|
. . 52 |
. . 291.1318 |
. . 1.0000 |
|
53 |
291.3020 |
1.0000 |
|
54 |
291.6690 |
1.0000 |
Uji kenormalan residual estimasi model VAR pada persamaan (14) menggunakan uji Lomnicki-Jarque-Bera (LJB).
Nilai statistik uji berupa nilai S3 , s4 , dan QB3 dapat dilihat pada Tabel 4.
Tabel 4. Nilai Chi-square Statistik Uji Kenormalan
|
Statistik Uji |
Chi-square |
df |
p-value |
|
sl |
5,06074 |
3 |
0,1674 |
|
S4 |
5,87238 |
3 |
0,1180 |
|
LJB3 |
10,93312 |
6 |
0,0905 |
Penarikan keputusan menggunakan tingkat signifikan 5%. Karena nilai p-value S3 , sI , dan LJBk lebih besar dari 5%, maka tidak cukup bukti untuk menolak Hq . Hal ini berarti, residual estimasi model VAR pada persamaan (14) menyebar normal.
Estimasi model VAR pada persamaan (14) stabil apabila modulus dari akar-akar reverse characteristics polynomial berada pada atau di dalam lingkaran unit. Modulus akar-akar dapat dilihat pada Tabel 5.
Tabel 5. Akar-Akar reverse characteristics polynomial
|
Akar |
Modulus |
|
0,713006 – 0,441929i |
0,838855 |
|
0,713006 + 0,441929i |
0,838855 |
|
0,702206 |
0,702206 |
|
0,429192 – 0,548102i |
0,696148 |
|
0,429192 + 0,548102i |
0,696148 |
|
-0,031031 |
0,031031 |
Nilai modulus akar-akar reverse characteristics polynomial pada Tabel 5 berada di dalam lingkaran unit. Jadi, estimasi model VAR dari data produksi perikanan tangkap laut (L), suhu permukaan laut (S) dan curah hujan (H) di NTT pada persamaan (14) adalah model yang stabil.
Ukuran keakuratan model dalam meramalkan dihitung mengguanakan persamaan (11) berupa nilai MAPE. Data aktual yang digunakan dalam menghitung nilai MAPE adalah data produksi perikanan tangkap laut, suhu permukaan laut dan curah hujan di NTT pada Maret 2017 sampai Desember 2017 dan data hasil peramalan diperoleh menggunakan model pada persamaan (14). Memperlihatkan bahwa nilai MAPE peramalan produksi perikanan tangkap laut, suhu permukaan laut dan
curah hujan di NTT berturut-turut adalah 16,17%; 3,08%; dan 4.505,4%. Berdasarkan Tabel 1 dan nilai MAPE maka peramalan produksi perikanan tangkap laut sangat akurat, peramalan suhu permukaan laut baik, sedangkan untuk curah hujan peramalan tidak akurat.
Setelah memperoleh model VAR, peramalan produksi perikanan tangkap laut, suhu permukaan laut dan curah hujan di NTT dari Januari 2018 sampai Juni 2018 dengan menggunakan estimasi model VAR persamaan (14) dapat dilihat pada Tabel 6.
Tabel 6. Peramalan Produksi Perikanan Tangkap Laut, Suhu Permukaan Laut, dan Curah Hujan di NTT Tahun 2018
|
Bulan |
L (dalam TON) |
S (dalam Derajat Celsius |
H (dalam Milimeter) |
|
Januari |
9.407,656 |
28,82236 |
148,8065 |
|
Februari |
9.378,990 |
28,78489 |
147,5714 |
|
Maret |
9.393,973 |
28,74935 |
143,1480 |
|
April |
9.427,204 |
28,72383 |
138,2300 |
|
Mei |
9.456,933 |
28,71128 |
134,7671 |
|
Juni |
9.473,076 |
28,71093 |
133,4214 |
Hasil perhitungan statistik uji untuk analisis kausalitas granger dapat dilihat pada Tabel 7, 8, dan 9.
Tabel 7. Kausalitas Granger Variabel Dependen Produksi Perikanan Tangkap Laut
|
Variabel |
F |
Prob. |
|
H |
1,00941 |
0,3719 |
|
S |
3,48361 |
0,0385 |
Berdasarkan Tabel 7 diperoleh bahwa p-value lebih kecil dari 0,05 sehingga keputusannya adalah menolak Hq , yang berarti suhu permukaan laut signifikan berpengaruh pada jumlah produksi perikanan tangkap laut. Sementara itu curah hujan memiliki p-value yang lebih besar dari 0,05 sehingga keputusannya tidak dapat menolak Hq atau curah
hujan tidak memiliki pengaruh terhadap produksi perikanan tangkap laut.
Tabel 8. Kausalitas Granger Variabel Dependen Suhu Permukaan Laut
|
Variabel |
F |
Prob. |
|
L |
0,06606 |
0,9362 |
|
H |
1,96366 |
0,1512 |
Berdasarkan Tabel 8 diperoleh bahwa p-value lebih besar dari 0,05 sehingga keputusannya adalah tidak dapat menolak Hq , yang berarti produksi perikanan tangkap laut dan curah hujan tidak memiliki pengaruh yang signifikan terhadap suhu permukaan laut.
Tabel 9. Kausalitas Granger Variabel Dependen Curah Hujan
|
Variabel |
F |
Prob. |
|
L |
1,07110 |
0,3505 |
|
S |
7,02910 |
0,0021 |
Berdasarkan Tabel 9 diperoleh bahwa p-value lebih kecil dari 0,05 sehingga keputusannya adalah menolak Hq , yang berarti suhu permukaan laut signifikan berpengaruh terhadap curah hujan. Sementara itu produksi perikanan tangkap laut memiliki p-value yang lebih besar dari 0,05 sehingga keputusannya tidak dapat menolak Hq atau produksi perikanan tangkap laut tidak memiliki pengaruh terhadap curah hujan.
-
b. Impulse Response Function (IRF)
Pada analisis IRF, dilihat respon satu variabel dalam menanggapi shock yang diberikan oleh variabel lain. Respon positif ditandai dengan grafik di atas garis nol, sedangkan grafik di bawah garis nol menunjukkan respon negatif. Fungsi respon impuls dari produksi perikanan tangkap laut, suhu permukaan laut dan curah hujan di NTT selama 25 periode.
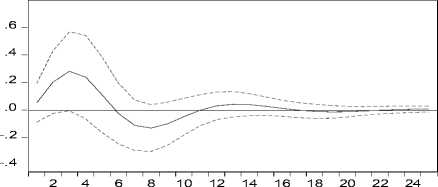
Pada Gambar 4, terlihat adanya pengaruh positif terhadap suhu permukaan laut setelah bulan pertama sampai bulan kelima dan setelah bulan kesebelas sampai bulan keenambelas
karena adanya shock dari curah hujan. Suhu permukaan laut mulai menunjukkan pengaruh negatif setelah bulan keenam sampai bulan kesepuluh. Setelah bulan keenambelas suhu permukaan laut cenderung stabil.
Response of S to H
Response S ± 2 S.E.
Gambar 4. Plot IRF Suhu Permukaan Laut Terhadap Curah Hujan
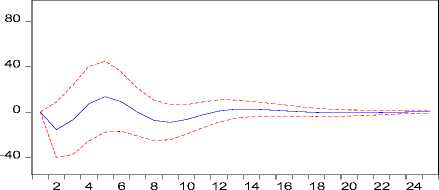
Response of S to L
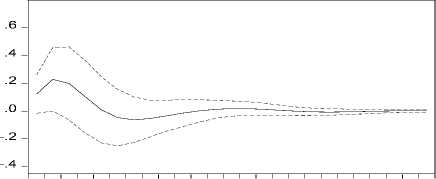
keduabelas sampai keenambelas karena adanya shock dari suhu permukaan laut. Curah hujan mulai menunjukkan pengaruh negatif setelah bulan ketujuh sampai bulan kesebelas dan bulan ke-18 sampai bulan ke-22. Setelah bulan ke-22 curah hujan cenderung stabil.
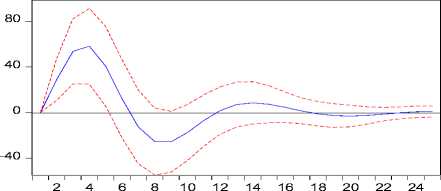
Response of H to L
I_____ Response H ± 2 S.E.
Gambar 7. Plot IRF Curah Hujan Terhadap Produksi Perikanan Tangkap Laut
2 4 6 8 10 12 14 16 18 20 22 24
Response S ± 2 S.E.
Gambar 5. Plot IRF Suhu Permukaan Laut Terhadap Produksi Perikanan Tangkap Laut
Pada Gambar 7, terlihat adanya pengaruh negatif terhadap curah hujan setelah bulan pertama sampai bulan ketiga dan bulan kedelapan sampai bulan ke sebelas karena adanya shock dari produksi perikanan tangkap laut. Curah hujan mulai menunjukkan pengaruh positif setelah tiga bulan keempat sampai bulan ketujuh. Setelah bulan kesebelas curah hujan cenderung stabil.
Pada Gambar 5, terlihat adanya pengaruh positif terhadap suhu permukaan laut setelah bulan pertama sampai bulan kelima karena adanya shock dari produksi perikanan tangkap laut. Suhu permukaan laut mulai menunjukkan pengaruh negatif setelah bulan keenam sampai bulan kesepuluh. Setelah bulan kesembilan suhu permukaan laut cenderung stabil.
Response of H to S
Response H ± 2 S.E.
Gambar 6. Plot IRF Curah Hujan Terhadap Suhu Permukaan Laut
Pada Gambar 6, terlihat adanya pengaruh positif terhadap curah hujan setelah bulan pertama sampai bulan keenam dan setelah bulan
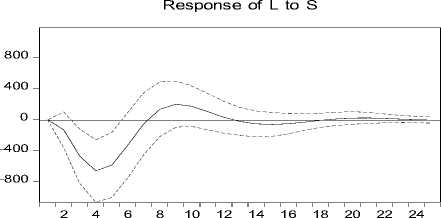
Response L ± 2 S.E.
Gambar 8. Plot IRF Produksi Perikanan Tangkap Laut Terhadap Suhu Permukaan Laut
Pada Gambar 8, terlihat adanya pengaruh negatif terhadap produksi perikanan tangkap laut setelah bulan pertama sampai bulan ketujuh dan bulan ke-13 sampai bulan ke-17 karena adanya shock dari suhu permukaan laut. produksi perikanan tangkap laut mulai menunjukkan pengaruh positif setelah bulan kedelapan sampai bulan ke-12. Setelah bulan ke-17 produksi perikanan tangkap laut cenderung stabil.
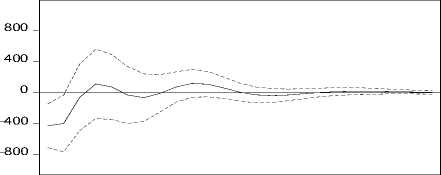
Response of L to H
2 4 6 8 10 12 14 16 18 20 22 24
Response L ± 2 S.E.
Gambar 9. Plot IRF Produksi Perikanan Tangkap Laut Terhadap Curah Hujan
Pada Gambar 9, terlihat adanya pengaruh negatif terhadap produksi perikanan tangkap laut setelah bulan pertama sampai bulan ketiga dan bulan keenam sampai bulan kedelapan karena adanya shock dari curah hujan. Produksi perikanan tangkap laut mulai menunjukkan pengaruh positif setelah bulan keempat sampai bulan kelima dan bulan kesembilan sampai bulan ke-12. Setelah bulan ke-13 produksi perikanan tangkap laut cenderung stabil.
5. KESIMPULAN
Berdasarkan hasil dan pembahasan, model vector autoregressive (VAR) dibentuk berdasarkan data produksi perikanan tangkap laut, suhu permukaan laut dan curah hujan di NTT memiliki orde optimum dua adalah sebagai berikut:
18173,68
11,22727
-1117,064
[H : ]=[
dengan
dan
0,992068
[8,749 × 10-≡
-0,022688
]+A1 [S ]+A2 [LS ]
Ht-1 Ht-2-l
-238,1576 1,263339 58,18294
-364,6648 -0,672192 -12,44571
-0,146694
Λ2=[-4,929×10 ^5 0,0114401
0,774217 0,002216], 0,7001698
3,678113 -0,001027
-0,3630004
Berdasarkan kriteria MAPE, peramalan
produksi perikanan tangkap laut sangat akurat, peramalan suhu permukaan laut baik, sedangkan untuk curah hujan peramalan tidak akurat.
Peramalan produksi perikanan tangkap laut di NTT (dalam ton) periode Januari 2018 sampai Juni 2018 yaitu sebanyak 9.407,656; 9.378,99; 9.393,973; 9.427,204; 9.456,933; 9.473,076,
suhu permukaan laut di NTT (dalam derajat celcius) periode Januari 2018 sampai Juni 2018
yaitu sebesar 28,8; 28,8; 28,7; 28,7; 28,7; 28,7 dan curah hujan di NTT periode Januari 2018 sampai Juni 2018 yaitu 148,8; 147,6; 143,1;
138,2; 134,8; 133,4. Berdasarkan uji kausalitas granger diperoleh suhu permukaan laut memengaruhi produksi perikanan tangkap laut dan curah hujan di NTT.
DAFTAR PUSTAKA
Bako, H., Rusima, M., Kane, I. & Matias-Peralta, H. 2013.Predictive Modeling of Pelagic Fish Catch in Malaysia Using Seasonal ARIMA models. Agriculture, Forestry and Fisheries, 3(3), pp.136-140.
BPS. 2018. Statistik Produksi Perikanan Tangkap di NTT 2015. [Online] Available at: https://www.bps.go.id/ [Accessed 1 April 2018].
Enders, W. (2015). Applied Econometrics Time Series. 4th ed. USA: John Wiley & Sons.
Gujarati, D.N. 2004. Basic Econometrics.4th ed. New York: McGraw-Hill.
Heizer, J., Render, B. & Munson, C. 2011. Operations Management Sustainability and Supply Chain Management. Boston: Pearson.
Lalli, C. & Parsons, T. 1997. Biological Oceanography: An Introduction. 2nd ed. Oxford: Elsevier Butterworth-Heinemann.
Lutkepohl, H., & Kratzig, M. 2004. Applied Time Series Econometrics. New York: Cambridge University Press.
Lutkepohl, H. 2005. New Introduction to Multiple Time Series Analysis. Berlin: Springer.
Perdana, T. & Susilowati, I. 2015. Dampak Perubahan Iklim Terhadap Perikanan Tangkap di Kota Semarang. Diponegoro Journal of Economics, 4(2), pp.1-7.
Ranangga, T., Sumarjaya, I. & Srinadi, I. 2018. Metode Vector Autoregresive (VAR) dalam Peramalan Jumlah Wisatawan Mancanegara ke Bali. E-Jurnal Matematika, 7(2), pp.157164.
Robinson, I. 2010. Discovering the Ocean from Space. Berlin: Springer.
Zhang, T., Wang, K. & Zhang, X. 2015. Modelling and Analyzing the Transmission Dynamics of HBV Epidemic in Xinjiang, China. Plos One, 10(9), pp.110-121.
163
Discussion and feedback