PERBANDINGAN PERAMALAN HASIL PRODUKSI IKAN MENGGUNAKAN METODE PERMULUSAN EKSPONENSIAL HOLT-WINTERS DAN ARIMA
on
E-Jurnal Matematika Vol. 7(4), November 2018, pp. 371-376
DOI: https://doi.org/10.24843/MTK.2018.v07.i04.p227
ISSN: 2303-1751
PERBANDINGAN PERAMALAN HASIL PRODUKSI IKAN MENGGUNAKAN METODE PERMULUSAN EKSPONENSIAL
HOLT-WINTERS DAN ARIMA
Dian Rahman1§, I Wayan Sumarjaya2, I Komang Gde Sukarsa3
-
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: diensar3@gmail.com] 2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id] 3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: sukarsakomang@yahoo.com]
§Corresponding Author
ABSTRACT
Every year fish consumption in Indonesia always increases. Basis landing of fish (PPI) Kedonganan is one of the ports where the ships docked and take part in economic activities of fisheries in Bali. The aim of this study is to forecast the amount of fish production so that the fish production can be managed. Some methods that can handle seasonal factors in time series forecasting include HoltWinters exponential smoothing and ARIMA. The results show that ARIMA(2,0,4)×(3,1,2)12 yields RMSE is 89,358 and MAPE is 0.81% whereas the value of fish outcomes prediction using HoltWinters exponential smoothing method yields RMSE is 119,158 and MAPE is 1.14%.
Keywords: ARIMA, Holt-Winters exponential smoothing.
Indonesia merupakan negara maritim yang memiliki luas wilayah perairan sebesar 3,25 juta km2 atau sekitar 63 persen dari total wilayah Indonesia (Keputusan Menteri Kelautan dan Perikanan, 2011). Letak geografi Indonesia yang diapit oleh dua samudera yakni Samudera Hindia dan Pasifik menjadikan sumber daya ikan memiliki nilai keragaman hayati yang tinggi di Indonesia.
Ikan merupakan salah satu sumber pangan yang dikonsumsi oleh masyarakat Indonesia. Setiap tahun konsumsi ikan selalu mengalami peningkatan. Peningkatan konsumsi ikan tahun 2011–2015 menunjukkan rata-rata persentase pertumbuhan sebesar 6,27 persen dengan rata-rata konsumsi ikan sebesar 36,12 kg/kapita/tahun (Kementerian Kelautan dan Perikanan Republik Indonesia, 2015).
Pangkalan Pendaratan Ikan (PPI) merupakan tempat berlabuh perahu atau kapal dan menjadi sarana kegiatan ekonomi perikanan. Terdapat 13 lokasi PPI yang tersebar di provinsi Bali, salah satu PPI yang berada di Bali adalah
PPI Kedonganan yang menjadi pengembangan kegiatan usaha perikanan.
Peramalan adalah salah satu cara untuk mengetahui dan memprediksi peristiwa yang akan terjadi pada masa yang akan datang dengan melihat kembali data yang telah lampau, sehingga dapat dinyatakan bahwa peramalan mempunyai peranan penting dalam mengambil keputusan di kemudian hari.
Menurut Nontji (2002) pola musim penangkapan ikan yang berlangsung dipengaruhi oleh pola arus dan perubahan pola arah angin, di Indonesia pola arus dan perubahan pola arah angin selalu berubah setiap tahun. Pola angin ini bertiup secara berkala di arah tertentu pada satu periode dan selanjutnya bertiup ke arah berlainan pula. Pola tersebut kerap dikenal dengan angin musim barat (Desember– Februari), angin musim timur (Juni–Agustus), dan musim peralihan (Maret–Mei dan September–November). Hal ini menunjukkan bahwa ada faktor musiman yang mempengaruhi hasil produksi ikan setiap tahun. Menurut
Makridakis et al. (1998) metode peramalan yang dapat menangani faktor musiman pada peramalan deret waktu adalah pemulusan eksponensial Holt-Winters dan autoregressive integrated moving average (ARIMA).
Pemulusan eksponensial adalah suatu metode peramalan rata-rata bergerak yang melakukan pembobotan menurun secara eksponensial terhadap nilai observasi yang lebih lama (Makridakis at al., 1998). Pemulusan
eksponensial Holt-Winters merupakan perluasan dari pemulusan eksponensial Holt yang dirancang untuk data runtun waktu yang mengandung musiman. Metode pemulusan eksponensial Holt-Winters dibagi menjadi dua yaitu pemulusan eksponensial Holt-Winters aditif dan multikatif. Pemulusan ekponensial Holt-Winters aditif digunakan untuk variasi musiman yang bersifat konstatan sedangkan pemulusan eksponensial Holt-Winters multikatif digunakan untuk variasi musiman yang mengalami fluktasi pada musimannya.
Menurut Montgomery et al. (2008) cara menentukan nilai awal taksiran untuk pemulusan eksponensial Holt-Winters aditif sebagai berikut. Inisialisasi data keseluruhan
L
Inisialisasi faktor tren
-
2, 1 ∫ ( Xl+ι - X1)( Xl+2 — X2)+ ( Xl+l - Xl ) 1
(2) Inisialisasi faktor musiman
dengan persamaan
Pemulusan eksponensial keseluruhan
St = α(Xt - It—l ) + (1 - α)(St-1 + bt-1).(4)
Pemulusan faktor tren
bt = β(St - St-1) + (1 - β)bt-1.(5)
Pemulusan faktor musiman
It = γ(Xt - St) + (1 - γ)It-l .
Ramalan m periode ke depan
Cara menghitung nilai awal taksiran pemulusan eksponensial Holt-Winters multikatif sama dengan model aditif kecuali untuk inisialisasi faktor musiman yaitu
I = X, I2 =—, ∙∙∙, Ii = XL
1S2S LS
.
dengan persamaan
Pemulusan eksponensial keseluruhan
St = α + (1 - α)(St-1 + bt-1).
It - L
Pemulusan faktor tren
bt = β(St - St -1) + (1 - β)bt-1.
Pemulusan faktor musiman
X
It = Y XX + (1 - Y) It - L.
St
Ramalan m periode ke depan
F+m = (St + btm) It - L+m.
(8)
(9)
(10)
(11)
(12)
ARIMA adalah salah satu metode peramalan deret waktu yang banyak digunakan dengan mengharuskan data memenuhi asumsi stasioneritas. Ada beberapa model yang dapat terbentuk dari deret waktu ARIMA di antaranya adalah model autoregresif (AR), model rerata bergerak (MA), model rerata bergerak autoregresif (ARMA), model rerata bergerak terintegrasi autoregresif (ARIMA) dan model rerata bergerak terintegrasi autoregresif musiman (SARIMA).
Suatu model ARIMA dibangun dengan beberapa asumsi. Uji kesesuaian model dilakukan untuk memeriksa asumsi model apakah galat model adalah white noise dan apakah model telah berdistribusi normal, selanjutnya menetapkan model terpilih dengan mengambil nilai AIC terkecil dari model.
Root mean square error (RMSE) dan mean absolute percentage error (MAPE) adalah salah satu cara untuk mengamati nilai kesalahan dalam suatu peramalan. Nilai RMSE dan MAPE dapat menjadi pembanding akurasi peramalan dari beberapa metode peramalan.
-
2. METODE PENELITIAN
Sumber Data
Data yang digunakan merupakan data sekunder yang diperoleh dari Pangkalan Produksi Ikan (PPI) Kedonganan, Kuta Selatan, Bali. Data produksi ikan yang digunakan untuk meramalkan hasil produksi ikan selama enam bulan adalah data bulanan dari bulan Januari 2011 – Februari 2018 di Pangkalan Produksi Ikan (PPI) Kedonganan, Kuta Selatan, Bali.
Teknik Analisis Data Pemulusanan Eksponensial Holt-Winters
Tahap-tahap yang dilakukan dalam menganalisis data pemulusan eksponensial HoltWinters sebagai berikut.
-
1. Membuat plot deret waktu untuk menentukan pola musiman aditif dan multikatif.
-
2. Menentukan panjang musiman (L) yaitu periode permusim, dalam hal ini panjang musiman adalah 12 karena data merupakan data perbulan.
-
3. Menentukan nilai awal taksiran pemulusan eksponensial awal (SL), tren (bL) dan musiman (IL).
-
4. Menentukan nilai alpha (α), beta (β), dan gamma (γ) yang memiliki sum of square error (SSE) yang minimum. Prosedur
optimasisasi ini dilakukan secara numerik, dalam hal ini menggunakan aplikasi R.
-
5. Menghitung pemulusan eksponensial keseluruhan (St), nilai tren (bt) dan nilai musiman (It).
-
6. Selanjutnya dari ketiga persamaan tersebut diperoleh nilai ramalan untuk m periode ke depan (Ft + m).
-
7. Mengamati nilai kesalahan peramalan menggunakan root mean squared error (RMSE) dan mean absolute percentage error (MAPE).
Teknik Analisis Data ARIMA
Tahapan-tahapan yang akan dilakukan untuk menganalisis pada metode ARIMA sebagai berikut:
-
1. Membuat plot deret waktu
-
2. Pemeriksaan kestasioneran dengan melihat grafik fungsi autokorelasi. Apabila pada grafik data telah menunjukkan pola yang cenderung lambat menuju nol pada beberapa lag awal maka data tersebut tidak stasioner, dan untuk lebih memastikan kembali akan dilakukan pengujian formal dengan menggunakan uji augmented Dickey Fuller (ADF).
-
3. Selanjutnya membuat plot autocorrelation function (ACF) dan partial autocorrelation function (PACF) dari data yang telah stasioner dalam rata-rata dan varians untuk melakukan pendugaan model sementara.
-
4. Setelah melakukan pendugaan model maka tahap selanjutnya melakukan penaksiran dan pengujian parameter dari model tersebut.
-
5. Pemilihan model ARIMA dapat dilakukan dengan menggunakan kriteria informasi Aikake (AIC) dengan pengambilan keputusan nilai terkecil merupakan model terbaik.
-
6. Jika parameter signifikan maka dilanjutkan dengan melakukan pemeriksaan diagnostik yaitu memeriksa uji autokorelasi residual dan normalitas residual.
-
7. Melakukan peramalan dari model terbaik
-
8. Mengamati nilai kesalahan peramalan menggunakan root mean squared error (RMSE) dan mean absolute percentage error (MAPE).
Perbandingan Hasil Pemulusan Eksponensial Holt-Winters dan ARIMA
Setelah mendapatkan masing-masing nilai RMSE dan MAPE dari kedua hasil peramalan, maka selanjutnya melakukan perbandingan dengan mengamati nilai RMSE dan MAPE terkecil merupakan peramalan terbaik pada penelitian ini.
Hal pertama yang dilakukan adalah melihat plot data yang akan diteliti. Adapun plot data produksi yang diperoleh dari Pangkalan Produksi Ikan (PPI) Kedonganan dapat dilihat pada Gambar 1.
ye∣ujnf
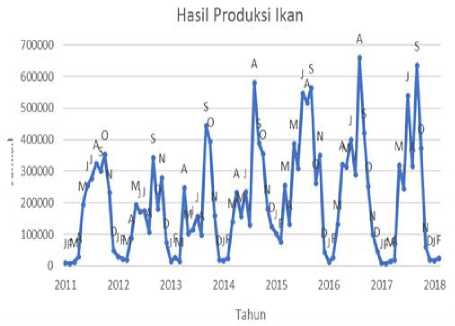
Gambar 1. Grafik Hasil Produksi Ikan
Huruf-huruf J, F, M, A, M, J, J, A, S, O, N, D yang terdapat pada Gambar 1. merupakan keterangan bulan pada jumlah produksi ikan setiap tahun. Terlihat pada grafik produksi ikan kerap mengalami kenaikan di antara bulan Agustus–Oktober dan selalu mengalami penurunan di antara bulan Januari–Maret. Hal ini mengindikasikan bahwa data pada hasil produksi ikan PPI Kedonganan mengandung faktor musiman.
Berdasarkan data yang telah diperoleh dari PPI Kedonganan menghasilkan bentuk pola seperti pada Gambar 1. dengan panjang musiman (L) sebesar 12 dan model musiman multikatif memperoleh nilai awal taksiran pemulusan eksponensial awal (SL) = 194.449,471; nilai awal taksiran pemulusan tren (bL) = -1.120,364 dan nilai awal faktor musiman (IL) dapat dilihat pada Tabel 1.
Tabel 1. Nilai Awal Taksiran Musiman
|
I1 |
-106.159,021 |
|
I2 |
-36.386,490 |
|
I3 |
63.586,873 |
|
I4 |
48.292,310 |
|
I5 |
121.185,463 |
|
I6 |
175.977,763 |
|
I7 |
206.641,757 |
|
I8 |
116.861,446 |
|
I9 |
-5.251,309 |
|
I10 |
-144.463,725 |
|
I11 |
-160.664,757 |
|
I12 |
-153.967,243 |
Prosedur optimalisasi yang dilakukan secara numerik dalam menentukan nilai α, β dan γ pada aplikasi R diperoleh model terbaik dengan sum of square error (SSE) minimum sebesar 1,050699×1012 dengan nilai α = 0,160; β = 0,018; dan γ = 0,157.
Selanjutnya melakukan peramalan untuk enam bulan ke depan dengan nilai α = 0,160; β = 0,018; dan γ = 0,157; sehingga diperoleh hasil ramalan dapat dilihat pada Tabel 2.
Tabel 2. Hasil Ramalan Holt-Winters Tahun
2018.
|
Bulan |
Hasil Produksi |
|
Maret |
87.170 |
|
April |
155.822 |
|
Mei |
254.675 |
|
Juni |
238.260 |
|
Juli |
310.033 |
|
Agustus |
363.705 |
-
3.2 ARIMA
Kestasioneran Data
Terlebih dahulu data ditransformasikan dengan menggunakan uji Box-Cox agar data stasioner dalam varians, diperoleh nilai uji BoxCox sebesar 0,174 sehingga akan dilakukan transformasi pada data dengan bentuk ln(X ) .
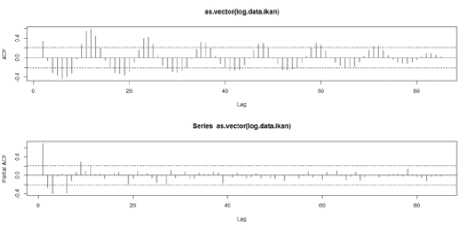
Gambar 2. ACF dan PACF Hasil Produksi Ikan
Plot ACF dan PACF pada Gambar 2. terlihat data menunjukkan pola yang tidak cenderung lambat menuju nol pada beberapa lag awal yakni lag kedua, sehingga dapat dikatakan bahwa data telah stasioner. Kemudian untuk memastikan kestasioneran data akan dilakukan pengujian formal melalui uji augmented Dickey Fuller (ADF) dengan bantuan program R diperoleh
nilai p-value sebesar 0,01 lebih kecil dari nilai α = 0,05 menunjukkan hipotesis nol ditolak sehingga dapat disimpulkan bahwa data telah stasioner.
Identifikasi Model
Model ARIMA Terpilih
Model ARIMA terpilih diperoleh dengan cara mencari nilai AIC terkecil dari kandidat model. ARIMA(2,0,4)×(3,1,2)12 adalah model terpilih dengan nilai AIC sebesar 1.942,3.
Setelah data stasioner maka langkah selanjutnya adalah mengindentifikasi model. Gambar 3. terlihat fungsi autokorelasi mengalami pengulangan di lag 12, 24, 48 yang menyatakan bahwa data mengandung unsur musiman yang kuat sehingga akan dilakukan differencing sebesar 12 terhadap faktor musiman.
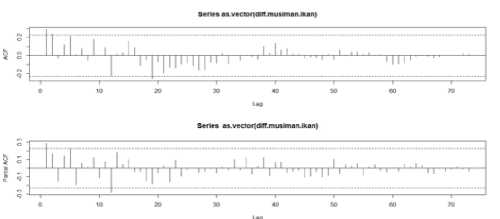
Gambar 3. ACF dan PACF Differencing Musiman
Estimasi Parameter Model
Kandidat model ARIMA dapat diperoleh dengan cara melihat pola tingkah laku pada fungsi autokorelasi dan fungsi autokorelasi parsial data. Adapun kandidat model ARIMA yang diperoleh pada penelitian ini disajikan pada Tabel 3.
Tabel 3. Kandidat-kanditat model ARIMA
|
No |
Model |
AIC |
|
1 |
ARIMA(2,0,0)×(1,1,0)12 |
1.950,0 |
|
2 |
ARIMA(2,0,0)×(1,1,2)12 |
1.948,9 |
|
3 |
ARIMA(2,0,0)×(2,1,0)12 |
1.951,2 |
|
4 |
ARIMA(2,0,0)×(2,1,2)12 |
1.948,5 |
|
5 |
ARIMA(2,0,0)×(3,1,0)12 |
1.946,7 |
|
6 |
ARIMA(2,0,0)×(3,1,2)12 |
1.949,5 |
|
7 |
ARIMA(2,0,3)×(1,1,0)12 |
1.954,0 |
|
8 |
ARIMA(2,0,3)×(1,1,2)12 |
1.952,2 |
|
9 |
ARIMA(2,0,3)×(2,1,0)12 |
1.955,1 |
|
10 |
ARIMA(2,0,3)×(2,1,2)12 |
1.951,5 |
|
11 |
ARIMA(2,0,3)×(3,1,0)12 |
1.948,4 |
|
12 |
ARIMA(2,0,3)×(3,1,2)12 |
1.951,6 |
|
13 |
ARIMA(2,0,4)×(1,1,0)12 |
1.955,2 |
|
14 |
ARIMA(2,0,4)×(1,1,2)12 |
1.950,9 |
|
15 |
ARIMA(2,0,4)×(2,1,0)12 |
1.949,0 |
|
16 |
ARIMA(2,0,4)×(2,1,2)12 |
1.944,4 |
|
17 |
ARIMA(2,0,4)×(3,1,0)12 |
1.942,3 |
|
18 |
ARIMA(2,0,4)×(3,1,2)12 |
1.944,9 |
Uji Diagnostik
Setelah melakukan pendugaan model maka langkah selanjutnya melakukan pemeriksaan uji autokorelasi residual dan normalitas residual pada model terpilih. Nilai uji autokorelasi residual Ljung-Box pada model terpilih adalah 0,3992 lebih besar dari nilai α = 0.05 menunjukkan hipotesis nol diterima sehingga dapat disimpulkan bahwa tidak ada korelasi antar data. Nilai uji normalitas Shapiro-Wilk pada model terpilih adalah 0,1023 lebih besar dari nilai α = 0.05 menunjukkan hipotesis nol diterima sehingga dapat disimpulkan bahwa data berdistribusi normal
Hasil Peramalan ARIMA
Hasil peramalan selama enam bulan ke depan yakni pada bulan Maret–Agustus 2018 dari model ARIMA(2,0,4)×(3,1,2)12 dapat dilihat pada Tabel 4.
Tabel 4. Hasil Ramalan ARIMA Tahun 2018
|
Bulan |
Hasil Produksi |
|
Maret |
73.279 |
|
April |
85.829 |
|
Mei |
223.721 |
|
Juni |
338.541 |
|
Juli |
349.167 |
|
Agustus |
469.998 |
RMSE dan MAPE
Berdasarkan kedua metode yang telah dianalisis maka diperoleh nilai masing-masing RMSE dan MAPE. Metode terbaik dipilih dengan mengambil nilai RMSE dan MAPE terkecil dari peramalan. Metode pemulusan eksponensial Holt-Winters dengan α = 0,160; β = 0,018; dan γ = 0,157 memperoleh nilai RMSE = 119.158 dan MAPE = 1,14%, sedangkan nilai kesalahan ramalan model
ARIMA(2,0,4)×(3,1,2)12 memperoleh nilai RMSE = 89.358 dan MAPE = 0,81 %.
Melihat nilai RMSE dan MAPE kedua metode dapat disimpulkan bahwa metode ARIMA lebih efektif dibandingkan metode pemulusan eksponensial Holt-Winters dalam kasus hasil produksi ikan di PPI Kedonganan dengan nilai kesalahan terkecil.
-
4. KESIMPULAN DAN SARAN
Kesimpulan
Berdasarkan hasil yang diperoleh dapat diambil kesimpulan bahwa pada kasus peramalan data produksi ikan di Pangkalan Produksi Ikan (PPI) Kedonganan lebih baik menggunakan metode ARIMA dengan nilai RMSE = 89.358 dan MAPE = 0,81%;
dibandingkan metode pemulusan eksponensial Holt-Winters dengan nilai RMSE = 119.158 dan MAPE = 1,14%.
Saran
Saran yang dapat diberikan penulis untuk peneliti selanjutnya dapat menggunakan metode lain yang bisa menangani faktor musiman seperti metode state space. Penulis berharap dengan melakukan peramalan menggunakan metode state space dapat memperoleh hasil peramalan yang lebih akurat dengan nilai kesalahan yang lebih kecil. Selain itu peneliti selanjutnya dapat melakukan peramalan pada musim angin barat di mana hasil produksi ikan yang sedikit dapat diramalkan guna memberi informasi kepada masyarakat serta instansi.
DAFTAR PUSTAKA
Kementrian Kelautan dan Perikanan Republik Indonesia, 2015, Konsumsi Ikan 20112015, http://statistik.kkp.go.id/sidatik-dev/Infografis/konsumsi-ikan-2011-2015.png, diakses 21 November 2017.
Keputusan Menteri Kelautan dan Perikanan Indonesia Nomor 45, 2011, Estimasi Potensi Sumber Daya Ikan di Wilayah Pengelolaan Perikanan Negara Republik Indonesia, http://kkji.kp3k.kkp.go.id/index.php/dokum en/regulasi-hukum/peraturan-menteri/finish/13-peraturan-menteri/161-permen-kp-no-45-tahun-2011-tentang-perubahan-atas-keputusan-menteri-kelautan-dan-perikanan-nomor-kep-56-men-2002-tentang-organisasi-dan-tata-kerja-akademi-perikanan-sorong, diakses 16 Desember 2017.
Makridakis, S., Wheelwright, SC., 1998, Forecasting Methods and Applications, 3rd ed. New York: Jhon Wiley & Sons, Inc.
Montgomery, D.C., Jennings, C.J., Kulahci, M., 2008, Introduction to Time Series Analysis and Forecasting, 1st ed, Canada: John Wiley & Sons, Inc.
Nontji, A., 2002, Laut Nusantara, Perseroan Terbatas. Djambatan, Jakarta..
376
Discussion and feedback