PENDEKATAN REGRESI NONPARAMETRIK DENGAN MENGGUNAKAN ESTIMATOR KERNEL PADA DATA KURS RUPIAH TERHADAP DOLAR AMERIKA SERIKAT
on
E-Jurnal Matematika Vol. 7(4), November 2018, pp. 305-310
DOI: https://doi.org/10.24843/MTK.2018.v07.i04.p218
ISSN: 2303-1751
PENDEKATAN REGRESI NONPARAMETRIK DENGAN
MENGGUNAKAN ESTIMATOR KERNEL PADA DATA KURS RUPIAH TERHADAP DOLAR AMERIKA SERIKAT
Dewa Ayu Dwi Astuti1§, I Gusti Ayu Made Srinadi2, Made Susilawati3
1Program Studi Matematika, Fakultas MIPA – UniversitasUdayana [Email: dewaastuti16@gmail.com] 2Program Studi Matematika, Fakultas MIPA – UniversitasUdayana [Email: srinadi@unud.ac.id] 3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: mdsusilawati@unud.ac.id]
-
§ Corresponding Author
ABSTRACT
Nonparametric regression can be applied for some data types one of them is time series data. The technique of this method is called smoothing technique. There are several smoothing techniques however this study used kernel estimator with seven kernel functions in data of rupiah exchange rate to US dollar. The analysis with R shows that by using minimum Generalized Cross Validation (GCV) criteria, seven functions produce various optimal bandwidth value but has similar curves estimation. The conclusion is that by using kernel estimator in time series data support that choosing the optimal bandwidth is more important than choosing the kernel functions.
Keywords: Nonparametric Regression, Kernel Estimator, Bandwidth, GCV.
Analisis regresi merupakan metode statistika yang digunakan untuk menentukan model atau pola hubungan antara variabel terikat/respon (dependent variable) dan variabel bebas/prediktor (independent variable). Pada umumnya, untuk melihat hubungan antara variabel terikat dan variabel bebas dapat dilakukan dengan dua pendekatan yaitu pendekatan parametrik dan pendekatan nonparametrik. Kedua pendekatan tersebut memiliki perbedaan terkait dengan asumsi-asumsi yang harus dipenuhi.
Model regresi parametrik mengasumsikan bahwa pola kurva regresi diketahui bentuknya seperti linear, kuadratik, kubik, polinomial derajat-p, eksponensial dan lain-lain. Pada model parametrik, ada beberapa asumsi yang harus dipenuhi seperti normalitas serta tidak terjadi autokorelasi, heteroskedastisitas, dan multikolinieritas. Sedangkan, model regresi nonparametrik tidak terikat pada asumsi bahwa kurva regresi diketahui bentuknya, dan membiarkan data mencari bentuk kurvanya sendiri. Pada model nonparametrik kurva regresi
diasumsikan termuat dalam suatu ruang fungsi berdimensi tak hingga dan merupakan fungsi yang mulus atau smooth (Eubank, 1999).
Teknik yang digunakan untuk mengestimasi fungsi maupun kurva regresi pada pendekatan nonparametrik adalah teknik pemulusan (smoothing). Adapun beberapa teknik smoothing dalam pendekatan regresi nonparametrik yaitu histogram, estimator kernel, estimator spline, estimator polinomial lokal, deret Fourier, deret orthogonal, k-NN (k-nearest neighbor), dan wavelet.
Penggunaan regresi nonparametrik dapat digunakan pada beberapa jenis data salah satunya yaitu data time series. Menurut Wuleng,dkk (2014), hal ini dikarenakan data time series yang sering fluktuatif serta galatnya diasumsikan saling berkorelasi perlu analisis tersendiri. Ada beberapa kasus data time series dianalisis menggunakan pendekatan nonparametrik (Hardle, 1994). Salah satu pendekatan nonparametrik yang dapat digunakan adalah pendekatan dengan menggunakan estimator kernel. Estimator kernel
memiliki tujuh macam fungsi yaitu triangle, Gauss, Epanechnikov, uniform, cosinus, triweight, dan quartic (Hardle, 1990).
Penelitian sebelumnya mengenai regresi nonparametrik pada data time series dilakukan oleh Wuleng,dkk (2014) yang memodelkan data kurs rupiah terhadap dolar Amerika Serikat dengan menggunakan Penalized Spline Filter yaitu salah satu bentuk penaksir regresi nonparametrik, dimana fungsi penaltinya menggunakan fungsi filter. Penelitian ini menghasilkan model optimal dengan menggunakan satu titik knot dan parameter penghalus λ = 0,001. Suparti,dkk (2014) menganalisis data inflasi Indonesia menggunakan model regresi polinomial lokal dengan kriteria generalized cross validation (GCV) minimum untuk menentukan titik lokal optimal. Hasil penelitian ini yaitu prediksi inflasi bulan Juni tahun 2016 sebesar 3,43 sedangkan Bank Indonesia mencatat inflasi bulan Juni tahun 2016 sebesar 3,45. Hal ini menunjukkan bahwa perbedaan nilai aktual dan prediksi tidak jauh berbeda.
Kurs atau nilai tukar mata uang merupakan salah satu data time series yang selalu mengalami fluktuasi. Fluktuasi terjadi karena penentuan nilai kurs mata uang suatu negara dengan mata uang negara lain ditentukan oleh permintaan dan penawaran mata uang yang bersangkutan (Novianto, 2011). Di Indonesia, kurs rupiah juga sering mengalami fluktuasi. Hal ini tentunya akan berpengaruh pada sektor perekonomian nasional karena kurs rupiah memegang peran penting dalam hubungan bilateral, seperti dalam dunia ekspor-impor dan harga saham.
Dolar Amerika Serikat merupakan mata uang resmi negara Amerika Serikat yang juga digunakan secara luas di dunia internasional. Nilai rupiah terhadap mata uang dolar ini sering melemah hingga mencapai harga yang jauh dari target pemerintah dalam Anggaran Pendapatan dan Belanja Negara (APBN). Sehingga nilai kurs rupiah terhadap mata uang dolar Amerika Serikat menjadi salah satu kasus nilai kurs yang paling sering mengalami fluktuasi.
Berdasarkan hal tersebut, maka peneliti tertarik untuk melakukan penelitian mengenai pendekatan regresi nonparametrik dengan menggunakan estimator kernel pada data kurs rupiah terhadap dolar Amerika Serikat.
Untuk n pengamatan yang independen, ( xi , Vt ) dengan i=1,2,…,n maka model regresi nonparametrik secara umum dapat ditulis dengan:
yt =(χt)+εi ,i=1,2,…,n (1) Vi adalah variabel terikat ke-i, f( xi ) adalah fungsi regresi yang tidak diketahui bentuk kurva regresinya dan εi adalah random error atau galat acak yang diasumsikan independen dan identik dengan rataan 0 dan ragam σ2 .
Salah satu teknik dalam regresi nonparametrik adalah estimator kernel. Estimator kernel diperkenalkan oleh Rosenblatt dan Parzen. Rosenblatt memberi bobot pada setiap pengamatan, dengan memilih fungsi K, sehingga pengamatan yang lebih dekat ke x akan memberi sumbangan yang lebih besar terhadap ̂h(X). Fungsi K ini merupakan fungsi pembobot yang dinamakan fungsi kernel (Hardle, 1994). Bentuk bobot kernel ditentukan oleh fungsi kernel K, sedangkan ukuran bobotnya ditentukan oleh parameter pemulus h yang disebut bandwidth.
Secara umum kernel K dengan bandwidth h (Wand & Jones, 1995) didefinisikan sebagai:
-
1 U\
κ^ ( “ )=ℎκ (ℎ) ,
untuk - ∞ < U< ∞ dan ℎ>0 (2)
serta memenuhi:
-
(a) K(u)≥0, untuk semuau,
-
(b) ∫ ∞∞ K(U) du=1,
-
(c) ∫ ∞ (u) du = >0,
-
(d) ∫∞ruK(u) du=0.
Adapun beberapa jenis fungsi kernel disajikan dalam Tabel 1.
Tabel 1. Jenis-jenis Fungsi Kernel
|
No. |
Fungsi Kernel |
Bentuk Fungsi |
|
1 |
Uniform |
1 K(U)= I (|u|≤21) |
|
2 |
Triangle |
K(U)=(1-|U|) I (|U|≤1) |
|
3 |
Epanechnikov |
3 K(U)=4(1-U2 ) I (|U|≤41) |
|
4 |
Quartic |
15 K(U)=16(1-U2)2 16 I (|U|≤1) |
|
5 |
Triweight |
35 K(U)=32(1-U2)3 I (|U|≤312) |
|
6 |
Gauss |
K(U) =√2 π exp(12(-U2)), -∞<U<∞ |
|
7 |
Cosinus |
Tl /71 x K(U)=4cos(2U) I (|U|≤41) 2 |
dengan I adalah fungsi indikator (Hardle, 1990).
Regresi kernel adalah salah satu teknik statistika nonparametrik yang dapat digunakan untuk menduga fungsi regresi f( xi ) pada model regresi nonparametrik pada persamaan (1). Pada tahun 1964, Nadaraya dan Watson mengusulkan penduga/estimator kernel dalam regresi nonparametrik yang kemudian sering disebut
dengan
estimator
Nadaraya-Watson
(Hardle,1990) yaitu:
̂(X)=
∑?=i Kfi (x- xi ) Vi
∑k=ικh(X- χk ) n
(3)
dengan
=∑WM (X) yl i=ι
(4)
Whi (X)=
(5)
(h)
∑nk^ (h) .
Selanjutnya, untuk memperoleh nilai duga
masing-masing pengamatan yaitu diperoleh:
n
] ̂( xi)=∑Whj (xi) yj
j = l
dengan
K( Xi-X] ) whj (xi )= ( )
∑ n^ (h) ;i,j=1,2,…,n.
xi , maka
(6)
(7)
Menurut Hastie dan Tibshirani (1990), pemilihan bandwidth jauh lebih penting dibandingkan dengan memilih fungsi kernel. Bandwidth (h) adalah parameter pemulus (smoothing) yang berfungsi untuk mengontrol kemulusan dari kurva yang diduga. Bandwidth yang terlalu kecil akan menghasilkan kurva yang undersmoothing yaitu kurva yang sangat kasar dan sangat fluktuatif, dan sebaliknya bandwidth yang terlalu lebar akan menghasilkan kurva yang oversmoothing yaitu kurva yang sangat mulus, tetapi tidak sesuai dengan pola data (Hardle, 1994). Oleh karena itu, perlu dipilih bandwidth yang optimal untuk menghasilkan kurva yang optimal.
Suatu kriteria untuk h akan dibatasi pada kelas penduga linear, dimana untuk setiap h ada matriks H(h) berukuran n×n , H(h) simetris dan semidefinit positif, sehingga f h= (ℎ) Y
dengan elemen-elemen H(h) adalah ^ij yang diperoleh dari menuliskan kembali persamaan (7) sebagai:
∑ . K' (Xj-Xk X
(Takezawa, 2006).
Salah satu metode untuk mendapatkan h optimal adalah dengan menggunakan kriteria generalized cross validation (GCV) (Eubank, 1999), yang didefinisikan sebagai berikut:
MSE
GCV(ℎ)= 2 (9)
(ntl^(I-H(ℎ))) (9)
dengan n
MSE=1 ∑(y, - fh (X1))(10) i=i
I menyatakan matriks identitas dan tr menyatakan trace/teras dari matriks (I-H(ℎ)).
Selain digunakan dalam penentuan nilai GCV, menurut Aydin (2007) MSE (mean square error) merupakan salah satu metode yang digunakan untuk mengukur ketepatan suatu estimator. Semakin kecil nilai MSE yang dihasilkan, maka semakin baik hasil estimasinya.
Regresi nonparametrik pada pemodelan data deret waktu menggunakan tiga konsep dasar pemodelan matematika (Hardle, 1994) sebagai berikut:
-
1. Model (S) yaitu suatu barisan stasioner {(Xi , Yi), i=1,2,…,n } (diperbolehkan dependen stokastik) telah diobservasi dan berdasarkan hasil observasi akan diestimasi:
-
2. Model (T) yaitu suatu runtun waktu { ,i≥1 } telah diobservasi dan akan
diprediksi X∏+l dengan:
-
3. Model (C) yaitu error observasi {^m } dalam model regresi dengan rancangan tetap
membentuk barisan variabel random yang berkolerasi.
Menurut Hardle (1994), permasalahan model (T) dapat dipetakan dengan permasalahan model (S) dengan mendefinisikan dalam runtun waktu { Zi ,i≥1 }, yaitu nilai lag1 sebagai Xl dan Zi sebagai Yi . Selanjutnya, masalah prediksi Zn+ι dari {Zi,i=1,2,…,n} dapat dipandang sebagai masalah pemulusan regresi untuk
{(Xi , Zi)} = {(Zi-I, Zi) ;i=1,2,…,n (14) Jadi, masalah prediksi {Zi } ekuivalen dengan mengestimasi persamaan (2.11) untuk runtun waktu dua dimensi {(Xl , Yi), i=1,2,…,n}. Selanjutnya fungsi f diestimasi dengan metode nonparametrik.
Salah satu data time series yang sering mengalami fluktuasi adalah kasus data nilai kurs atau nilai tukar mata uang. Menurut Triyono (2008), kurs (exchange rate) adalah pertukaran antara dua mata uang yang berbeda, yaitu merupakan perbandingan nilai atau harga antara kedua mata uang tersebut. Ada beberapa macam kurs, antara lain:
-
(a) Kurs jual yaitu kurs yang digunakan apabila bank/money changer membeli valuta asing atau apabila seseorang ingin menukarkan valuta asing yang dimiliki dengan rupiah.
-
(b) Kurs beli yaitu kurs yang digunakan apabila bank/money changer menjual valuta asing atau apabila seseorang ingin menukarkan rupiah dengan valuta asing yang dibutuhkan.
-
(c) Kurs tengah yaitu kurs rata-rata antara kurs jual dan kurs beli.
Data yang digunakan dalam penelitian ini adalah data sekunder yaitu data harian kurs jual rupiah terhadap dolar Amerika Serikat periode tanggal 30 Juni 2017 sampai dengan 28 Februari 2018 yang diambil dari http://www.bi.go.id.
Adapun objek penelitian yang dijadikan variabel independen adalah data kurs rupiah terhadap dolar Amerika Serikat periode tanggal 30 Juni 2017 sampai dengan 27 Februari 2018. Sedangkan, objek penelitian yang dijadikan variabel dependen yaitu data kurs rupiah terhadap dolar Amerika Serikat periode tanggal 1 Juli 2017 sampai dengan 28 Februari 2018.
Dalam penelitian ini estimasi kurva regresi dilakukan dengan menggunakan estimator
kernel, dengan tujuh fungsi kernel yaitu uniform, triangle, Epanechnikov, quartic, triweight,
Gauss, dan cosinus. Penelitian ini menggunakan bantuan software R x64 3.4.3 dengan langkah-langkah yang dilakukan adalah sebagai berikut:
-
1. Mengubah data harian kurs jual rupiah
terhadap dolar Amerika Serikat periode 30 Juni 2017 sampai dengan 28 Februari 2018 berdasarkan persamaan (14) dengan = 243.
-
2. Menentukan nilai bandwidth optimal
masing-masing fungsi kernel.
-
3. Menggunakan bandwidth optimal untuk
memperoleh hasil estimasi kurva regresi nonparametrik masing-masing fungsi kernel.
-
4. Membandingkan hasil estimasi ketujuh fungsi kernel dengan membandingkan plot estimasi kurva regresi bersama-sama
dengan plot data, serta melihat nilai MSE yang dihasilkan.
Plot Data Kurs Rupiah/Dolar Amerika Serikat
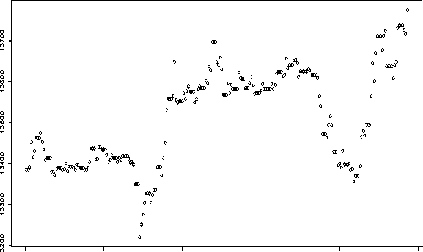
0 50 100 150 200 250
Waktu (Hari)
Gambar 1. Plot Data Harian Kurs Rupiah terhadap Dolar Amerika Serikat Periode 1 Juli 2017 – 28 Februari 2018
Gambar 1 memperlihatkan bahwa plot data kurs rupiah terhadap dolar Amerika Serikat pada periode tersebut tidak membentuk pola linear karena selama periode delapan bulan tersebut nilai kurs rupiah terhadap dolar Amerika Serikat cenderung mengalami fluktuasi sehingga penggunaan analisis regresi berganda tidak dapat diterapkan. Berdasarkan hal tersebut, maka pada penelitian ini data kurs rupiah terhadap dolar Amerika Serikat akan diestimasi dengan menggunakan pendekatan nonparametrik.
Langkah pertama untuk mengestimasi kurva regresi dengan menggunakan estimator kernel adalah menentukan nilai bandwidth optimal masing-masing fungsi kernel yang digunakan yaitu uniform, triangle, Epanechnikov, quartic, triweight, gauss, dan cosinus. Nilai bandwidth optimal diperoleh berdasarkan kriteria nilai GCV (Generalized Cross Validation) yang minimum. Berdasarkan persamaan (2.9), terlihat bahwa besar kecilnya nilai GCV bergantung pada nilai MSE (Mean Square Error), bandwidth (h'), dan trace dari matriks H(h).
Secara ringkas nilai bandwidth optimal ketujuh fungsi kernel disajikan pada Tabel 2. Tabel 2 menunjukkan nilai bandwidth optimal masing-masing fungsi kernel dengan nilai GCV minimumnya. Tabel tersebut memperlihatkan bahwa masing-masing fungsi kernel memiliki nilai bandwidth optimal yang bervariasi.
Tabel 2. Nilai Bandwidth Optimal Fungsi Kernel
|
Fungsi Kernel |
Nilai Bandwidth Optimal |
Nilai GCV |
|
Uniform |
5,00 |
712,3605 |
|
Triangle |
9,70 |
715,8937 |
|
Epanechnikov |
7,05 |
714,4010 |
|
Quartic |
8,55 |
718,2056 |
|
Triweight |
11,05 |
717,4295 |
|
Gauss |
3,95 |
715,3156 |
|
Cosinus |
7,10 |
715,6449 |
Sumber: data diolah (2018)
Selanjutnya, nilai bandwidth optimal tersebut digunakan untuk memperoleh hasil estimasi kurva regresi nonparametrik ketujuh fungsi kernel. Adapun hasil estimasi kurva ketujuh fungsi kernel disajikan pada Gambar 2. Gambar 2 menunjukkan bahwa ketujuh fungsi kernel dengan masing-masing nilai bandwidth optimalnya menghasilkan kurva yang hampir mirip dan mengikuti pola data aktual.
Perbandingan Hasil Estimasi Fungsi Kernel

150
200
250
0
50
100
Waktu (Hari)
Gambar 2. Perbandingan Hasil Estimasi Ketujuh Fungsi Kernel
Data Aktual Uniform Epanechnikov Cosinus Quartic Triweight Gauss Triangle
Selanjutnya, untuk melihat ketepatan estimasi ketujuh fungsi kernel berikut disajikan nilai MSE yang dihasilkan oleh masing-masing fungsi kernel.
Tabel 3 memperlihatkan nilai MSE yang dihasilkan oleh ketujuh fungsi kernel. Nilai MSE menunjukkan seberapa bagus hasil estimasi yang dihasilkan oleh estimator kernel dengan menggunakan fungsi kernel Uniform, Triangle, Epanechnikov, Quartic, Triweight, Gauss, dan Cosinus. Semakin kecil nilai MSE yang dihasilkan, maka berarti semakin bagus hasil estimasinya.
Tabel 3. Nilai MSE masing-masing Fungsi Kernel
|
No |
Fungsi Kernel |
Nilai MSE (mean square error) |
|
1 |
Uniform |
494,8126 |
|
2 |
Triangle |
501,2490 |
|
3 |
Epanechnikov |
488,8835 |
|
4 |
Quartic |
490,7947 |
|
5 |
Triweight |
504,2970 |
|
6 |
Gauss |
502,5406 |
|
7 |
Cosinus |
485,7985 |
Sumber: data diolah (2018)
Ketujuh fungsi kernel menghasilkan MSE yang nilainya tidak jauh berbeda antara satu sama lain sehingga dari nilai MSE tersebut dapat memperkuat bahwa ketujuh fungsi kernel menghasilkan estimasi kurva yang mirip. Hal ini mendukung pendapat Hastie & Tibshirani (1990) yang menyatakan bahwa pemilihan bandwidth jauh lebih penting dibandingkan pemilihan fungsi kernel dikarenakan telah terbukti pemilihan fungsi kernel yang berbeda akan menghasilkan estimasi kurva yang hampir sama.
Pendekatan regresi nonparametrik dengan estimator kernel menggunakan fungsi kernel Uniform, triangle, epanechnikov, quartic, triweight, gauss, dan cosinus pada data kurs rupiah terhadap dolar Amerika Serikat menghasilkan nilai bandwidth optimal yang bervariasi. Namun, dengan menggunakan nilai bandwidth optimal menghasilkan kurva regresi yang berimpit dan mengikuti pola data aktual. Dilihat berdasarkan nilai MSE (mean square error) yang dihasilkan, masing-masing fungsi memiliki nilai MSE yang tidak jauh berbeda antara satu sama lain sehingga memperkuat bahwa ketujuh fungsi menghasilkan estimasi kurva yang hampir sama. Jadi, dapat dikatakan bahwa penerapan estimator kernel pada data time series juga menghasilkan kesimpulan bahwa pemilihan bandwidth jauh lebih penting dibandingkan dengan pemilihan fungsi kernel.
DAFTAR PUSTAKA
Aydin, D. (2007). A Comparison of the Nonparametric Regression Models using Smoothing Spline and Kernel Regression. World Academy of Science, Engineering and Technology, 36, 253-257, Turkey.
Bank Indonesia. (2018).
http://www.bi.go.id/id/moneter/informasi-kurs/transaksi-bi/Default.aspx. Diakses
tanggal 10 Maret 2018.
Eubank, R. L. (1999). Nonparametric Regression and Spline Smoothing. New York: Marcel Dekker.
Hardle, W. (1994). Applied Nonparametric Regression. New York: Cambridge
University Press.
Hardle, W. (1990). Smoothing Techniques with Implementation in S. New York: Cambridge University Press.
Hastie, T., & Tibshirani, R. (1990). Generalized Additive Models. New York: Chapman and Hall.
Novianto,Aditya. (2011). " Analisis Pengaruh Nilai Tukar (Kurs) Dolar Amerika/Rupiah (US$/Rp), Tingkat Suku Bunga SBI, Inflasi, dan Jumlah Uang Beredar (M2) terhadap Indeks Harga Saham Gabungan (IHSG) di Bursa Efek Indonesia (BEI) periode 1999.1 – 2010.6". Skripsi. Fakultas Ekonomi Universitas Diponegoro.
Semarang.
Suparti, Warsito, B., & Mukid, M. A. (2014). Analisis Data Inflasi di Indonesia Menggunakan Model Regresi Polinomial Lokal. IndoMS Journal on Statistics , II, 65-78.
Takezawa, K. (2006). Introduction to Nonparametric Regression. New Jersey: John Wiley & Sons,Inc.
Triyono. (2008). Analisis Perubahan Kurs Rupiah terhadap Dolar Amerika Serikat. Jurnal Ekonomi Pembangunan , IX, 156167. Universitas Muhammadiyah
Surakarta.
Wand, M., & Jones, M. (1995). Kernel
Smoothing. New York: Chapman and Hall.
Wuleng,A.T., Islamiyati,A., & Herdiani, E.T. (2014). http://repository.unhas.ac.
id/bitstream/handle/123456789/10741/ JURNAL.pdf?sequence=1. Diakses tanggal 7 Oktober 2017.
310
Discussion and feedback