ESTIMASI NILAI IMPLIED VOLATILITY MENGGUNAKAN SIMULASI MONTE CARLO
on
E-Jurnal Matematika Vol. 7(3), Agustus 2018, pp. 239-245
DOI: https://doi.org/10.24843/MTK.2018.v07.i03.p209
ISSN: 2303-1751
ESTIMASI NILAI IMPLIED VOLATILITY MENGGUNAKAN SIMULASI MONTE CARLO
Makbul Muflihunallah¹§, Komang Dharmawan², Ni Made Asih³
¹Program Studi Matematika, Fakultas MIPA–Universitas Udayana [Email: muflihunallah@gmail.com]
²Program Studi Matematika, Fakultas MIPA–Universitas Udayana [Email: k.dharmawan@unud.ac.id]
³Program Studi Matematika, Fakultas MIPA–Universitas Udayana [Email: madeasih@unud.ac.id] §Corresponding Author
ABSTRACT
Investing among investors is an exciting activity to gain profit in the financial world. The development of investment in the financial world affects the number of alternative investment instruments that can be offered to investors in the capital market. The management of instruments in finance depends on the accuracy of forecasting of variables for example volatility. Volatility is a statistic of the degree of price variation in one period to the next which is expressed by σ. Volatility values can be estimated using Implied Volatility. Implied Volatility is the volatility used in determining the price of European options obtained by equalizing the price of the theoretical options, the price obtained from the Black-Scholes model, with the option price in the market. In this research will discuss how to estimate Implied Volatility value using the option obtained from simulation with Monte Carlo.
Keywords: Implied Volatility, Monte Carlo
1. PENDAHULUAN
Berinvestasi dikalangan investor adalah kegiatan yang menarik untuk mendapatkan keuntungan yang optimal. Instrumen yang dapat digunakan untuk memperoleh keuntungan dalam berinvestasi salah satunya instrumen derivatif. Instrument derivatif merupakan suatu kontrak atau perjanjian penukaran pembayaran yang nilainya bergantung pada nilai dari aset lain yang lebih mendasar, sebagai contohnya kontrak opsi dengan aset dasar saham.
Kontrak opsi saham adalah suatu perjanjian atau kontrak yang terjadi di antara penjual dan pembeli opsi saham, dimana penjual menjamin adanya hak dan bukan merupakan suatu kewajiban kepada pembeli opsi saham untuk membeli atau menjual saham pada waktu tertentu dan harga yang telah disepakati (Brigham dan Houston, 2011). Semakin berkembangnya pasar opsi saham, maka semakin berkembang juga pengetahuan dalam memprediksi suatu pergerakan harga kontrak opsi saham dan memperkirakan segala kemungkinan yang bisa terjadi, dengan tujuan
untuk meminimalkan kerugian dan memaksimalkan keuntungan. Salah satu perusahaan yang menjual kontrak opsi saham adalah Perseroan Terbatas Telekomunikasi Indonesia,Tbk. (PT. Telkom). PT Telkom merupakan sebuah perusahaan Badan Usaha Milik Negara (BUMN) di Indonesia yang menyediakan layanan jaringan dan telekomunikasi diantaranya layanan InfoComm, telepon rumah, telepon seluler, dan internet (www.telkom.co.id).
Pengelolaan instrumen dalam dunia keuangan bergantung pada akurasi peramalan beberapa peubah (variables) sebagai contoh volatilitas (volatility). Faktor volatilitas atau volatility merupakan pengukuran statistik dari derajat variasi harga pada satu periode ke periode selanjutnya yang dinyatakan dengan σ (Lya Aklimawati, 2013). Meningkatnya volatilitas menyebabkan probabilitas untuk memperoleh harga aset dasar yang lebih tinggi atau lebih rendah pada saat opsi jatuh tempo juga akan meningkat. Maka dari itu penafsiran nilai volatilitas perlu dilakukan karena nilai volatilitas bergerak secara random dan tidak
dapat diobservasi secara langsung (Dharmawan & Widana, 2011).
Nilai volatilitas dapat diestimasi menggunakan data historis harga saham, seperti harga saham pembukaan (open), harga saham penutupan (close), harga saham terendah (low), dan harga saham tertinggi (high) (Garman & Klass, 1980). Selain itu, volatilitas dapat di estimasi menggunakan metode Monte Carlo (Changiagi, 2000), metode GARCH (Duan, 1995), metode Heston dan Implied Volatility (Renault & Touzi, 1996). Menentukan nilai Implied Volatility yakni diberikannya harga opsi dan nilai S, T, K, dan r diketahui, kemudian nilai volatilitas (σ) ditentukan. Implied Volatility adalah volatilitas yang digunakan dalam penentuan harga opsi Eropa yang diperoleh dengan cara menyamakan harga opsi teoritis, harga yang diperoleh dari model Black-Scholes, dengan harga opsi yang di pasar.
Berdasarkan latar belakang yang telah diuraikan, peneliti tertarik menggunakan nilai opsi yang diperoleh dari hasil simulasi Monte Carlo, hal tersebut dikarenakan tidak mudah untuk memilih jenis opsi dan waktu jatuh tempo yang sama di pasar modal yang berbeda.
Simulasi Monte Carlo Standar, disebut juga Crude Monte Carlo, adalah suatu metode yang melibatkan pembangkit bilangan acak dengan distribusi probabilitas yang dapat diketahui dan ditentukan. Dasar simulasi Monte Carlo Standar adalah melakukan percobaan pada elemen-elemen probabilistik melalui pengambilan sampel acak. Metode ini telah diterapkan dalam berbagai bidang salah satunya pada bidang keuangan untuk menghitung ekspektasi payoff harga saham dan akhinya dapat digunakan untuk menentukan nilai opsi. Ekspetasi payoff dalam kondisi resiko netral dihitung dengan menggunakan prosedur sampling, kemudian didiskonto pada suku bunga bebas risiko (Hull, 2009).
Penentuan harga opsi pada simulasi Monte Carlo dipengaruhi oleh harga opsi dalam keadaan risiko netral (r = μ) Dalam simulasi Monte Carlo Standar, harga opsi diasumsikan mengikuti Gerak Brown Geometrik. Gerak
Brown Geometrik dalam perhitungan simulasi Monte Carlo Standar mengikuti persamaan
(1∆ + σ√∆t
st = Sto e∖ (1)
Kontrak opsi (option contract) merupakan suatu kontrak yang memberikan hak kepada pemegangnya namun bukan kewajiban untuk membeli (atau menjual) suatu aset pada harga yang telah ditentukan sebelumnya dalam jangka waktu tertentu (Brigham dan Houston, 2011). Jenis Sekuritas yang bisa dijadikan Opsi tidak hanya saham tetapi bisa dalam bentuk indeks pasar, kurs valuta asing, komoditas dan lain-lain. Menurut Tandelilin (2010) harga sebuah opsi akan dipengaruhi oleh enam faktor berikut ini
-
1. Harga saham yang dijadikan patokan;
-
2. Srike price yang ditetapkan;
-
3. Expriration date dari opsi;
-
4. Volatilitas harga saham yang diharapkan selama umur opsi;
-
5. Tingkat suku bunga jangka pendek selama umur opsi;
-
6. Deviden yang diharapkan diberikan oleh saham yang dijadikan patokan dalam opsi selama umur opsi tersebut.
Model Black-Scholes merupakan model penilaian call option standar yang banyak diterima oleh masyarakat keuangan. Model Black-Scholes hanya dapat digunakan untuk opsi dengan tipe Eropa (European Option) yang dilaksanakan pada saat waktu jatuh tempo (expiration date) dan mengasumsikan bahwa variansi atau volatilitas harga saham bersifat konstan selama usia opsi diketahui pasti. Selain itu model Black-Scholes hanya dapat diterapkan pada saham yang tidak memberikan dividend. Menurut Tandelilin (2010) model ini dikembangkan oleh Fisher Black dan Mryon Scholes. Rumus yang digunakan tidak begitu kompleks bahkan sudah tersedia pada kalkulator dan komputer Terdapat lima input yang dibutuhkan pada model Black-Scholes yaitu sebagai berikut :
-
1. Harga saham saat ini (S0);
-
2. Strike Price (K);
-
3. Expiration date ( T} -,
-
4. Tingakat suku bunga dalam satu tahun (r);
-
5. Volatilitas Harga saham (s).
Menurut Tandelilin (2010) rumus penilaian opsi dengan menggunakan model Black-Scholes adalah :
C = S0N(d 1) - Ke~rτN(d2)
(2)
dengan
d i —
ln ⅛) + (r + s2∕2)T [Jf
d2 — d 1 — s[T
Volatilitas (volatility) merupakan pengukuran statistik dari derajat variasi harga pada satu periode ke periode selanjutnya yang dinyatakan dengan σ (Lya Aklimawati, 2013). Ukuran tersebut menunjukkan penurunan dan peningkatan harga dalam periode yang pendek dan tidak mengukur tingkat harga, namun derajat variasinya dari satu periode ke periode berikutnya. Volatilitas tinggi mengakibatkan harga opsi menjadi mahal. Menurut Schwert (1992) terdapat lima jenis volatilitas dalam pasar keuangan, yaitu :
-
1. Future Volatility
Future volatility adalah apa yang hendak diketahui oleh para pemain dalam pasar keuangan (trader).
-
2. Historical Volatility
Untuk dapat mengetahui masa depan maka perlu mempelajari masa lalu. Hal ini dilakukan dengan membuat suatu pemodelan dengan teori pricing berdasarkan data masa lalu untuk dapat meramalkan volatilitas pada masa yang akan datang.
-
3. Forecast Volatility
Seperti halnya terdapat jasa yang berusaha meramalkan pergerakan arah masa depan harga suatu kontrak demikian juga terdapat jasa yang berusaha meramalkan volatilitas masa depan suatu kontrak
-
4. Seasonal Volatility
Seasonal Volatility adalah volatilitas yang mengalami musiman, contohnya komoditas pertanian tertentu seperti jagung, kacang kedelai, dan gandum yang sangat sensitif
terhadap factor-faktor dari kondisi cuaca musim yang jelek.
-
5. Implied Volatility
Implied Volatility merupakan volatilitas yang harus kita masukkan ke dalam model teoritis pricing untuk menghasilkan nilai teoritis yang identik dengan harga opsi di pasar. Berdasarkan keadaan persaingan pasar, Black-Scholes menunjukkan bahwa harga suatu saham (S) mengikuti gerak Brown geometric pada suku bunga dan fluktuasi saham tertentu (volatilitas). Pergerakan harga saham tersebut dapat ditulis dalam bentuk sebagai berikut
dS t — s^t + s S t d Wt (3)
dengan
dSt : perubahan harga saham yang mengikuti gerak Brown geometric
μ : rata-rata dari tingkat pengembalian
saham
d t : perubahan waktu
s : nilai volatilitas
Wt : gerak Brownian.
Menurut Lee (2002), keadaan pasar yang demikian dikatakan tidak ada arbitrase. Dengan kata lain, pelaku pasar modal mengasumsikan bahwa harga opsi di pasar modal sama dengan harga teoritis yang dihitung mengunakan model Black-Scholes, atau dapat ditulis sebagai berikut:
Cobs — Cbs (4)
dengan Cobs menyatakan harga opsi observasi yang diperoleh dari harga pasar sebenarnya, dimana masa jatuh tempo ( T) opsi sama dengan masa jatuh tempo ( T) saham induk. Dalam hal ini, Bss menyatakan harga opsi teoritis dari model Black-Scholes.
Jenis data yang digunakan dalam penelitian ini adalah data sekunder yakni data historis saham PT. Telekomunikasi Indonesia selama satu tahun terakhir yaitu data harian dari periode waktu 22 November 2016 sampai 22 November 2017. Sumber data dari penelitian ini diperoleh dari http://finance.yahoo.com/. Langkah-langkah penelitian meliputi:
-
1. Mengumpulkan data historis dari harga PT. Telekomunikasi Indonesia
-
2. Menghitung tingkat pengembalian (return) dari data historis harga PT. Telekomunikasi Indonesia
-
3. Mensimulasikan harga saham 1 tahun
menggunakan simulasi Monte Carlo
Standar. Simulasi dilakukan sebanyak 3000 kali
-
4. Menentukan input yang diperlukan pada model Black-Scholes dalam menentukan harga opsi dari masing-masing simulasi harga saham yaitu nilai harga aset saat ini (S0), strike price dari opsi (K), waktu jatuh tempo (T), suku bunga bebas risiko (r) dan volatilitas (σ)
-
5. Menghitung nilai opsi dari masing-masing simulasi harga saham dengan waktu jatuh tempo satu tahun menggunakan model Black- Scholes dan tentukan rataan dari hasil seluruh opsi yang diperoleh
-
6. Menghitung nilai Implied Volatility berdasarkan nilai rataan opsi hasil simulasi yang diperoleh dengan membangkitkan nilai volatility yang memungkinkan. Nilai tersebut kemudian diuji dan dipilih nilai yang menghasilkan nilai opsi paling mendekati nilai opsi simulasi sebagai Implied Volatility.
Pada penelitian ini menggunakan data historis harian harga saham penutupan PT. Telekomunikasi Indonesia periode waktu 22 November 2016 sampai 21 November 2017 sebanyak 253 data. Sumber data dari penelitian ini diperoleh dari http://finance.yahoo.com/ yang disajikan dalam bentuk plot pada Gambar 1.
Plot harga saham PT. Telekomunikasi Indonesia pada Gambar 1 menunjukkan harga saham mengalami kenaikan pada bulan Maret sampai dengan bulan September dan terlihat juga harga saham mengalami penurunan pada bulan September sampai dengan bulan November.
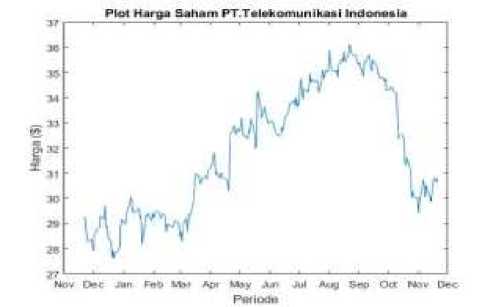
Gambar 1. Plot Harga Saham PT.
Telekomunikasi Indonesia Periode 22 November 2016 sampai 21 November 2017
Menghitung Nilai Return
Menghitung nilai return (R) pada waktu t pada harga penutupan saham PT. Telekomunikasi Indonesia menggunakan persamaan berikut :
R = l"⅛)
Hasil dari return saham dapat dilihat pada Gambar 2.
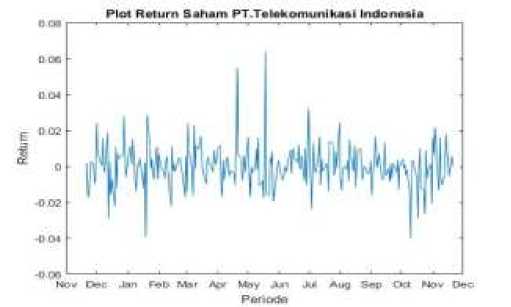
Gambar 2. Plot Return Saham PT. Telekomunikasi Indonesia Periode 22 November 2016 sampai 21 November 2
Plot return saham pada gambar 2 terlihat nilai tingkat pengembalian (return) saham PT. Telekomunikasi Indonesia pada bulan April dan Juni sangat tinggi dibandingkan dengan bulan-bulan lainnya, hal ini berarti adanya tingkat risiko yang relative lebih tinggi.
Setelah return dari semua data diperoleh dapat ditentukan nilai statistika deskriptif dari
return saham PT. Telekomunikasi Indonesia dapat dilihat pada Tabel 1.
Tabel 1. Nilai Statistika Deskriptif
|
No |
Karakteristik |
Nilai |
|
1 |
Mean |
0.000214 |
|
2 |
Variance |
0.000143 |
|
3 |
Standar deviasi |
0.011956 |
|
4 |
Maksimum |
0.063585 |
|
5 |
Minimum |
-0.04027 |
dari Tabel 1 dapat dilihat bahwa return harga saham PT. Telekomunikasi Indonesia mengalami fluktuasi data dengan nilai variance 0.00143 dan nilai rata-rata 0.000214 serta memiliki nilai maksimum dan minimum secara berturut-turut yaitu 0.063585 dan -0.04027.
Simulasi Harga Saham
Pada tahap sebelumnya telah diperoleh nilai mean, variance, dan standar deviasi yang dibutuhkan untuk melakukan simulasi pada harga saham PT. Telekomunikasi Indonesia untuk satu tahun yang akan datang. Tujuan dari melakukan simulasi dalam penelitian ini adalah untuk memprediksi harga-harga saham dimasa yang akan datang. Dalam penelitian ini jumlah simulasi sebanyak 3000 kali dengan menggunakan simulasi Monte Carlo Standar. Contoh hasil perhitungan dari 10 simulasi yang disajikan pada Gambar 3.
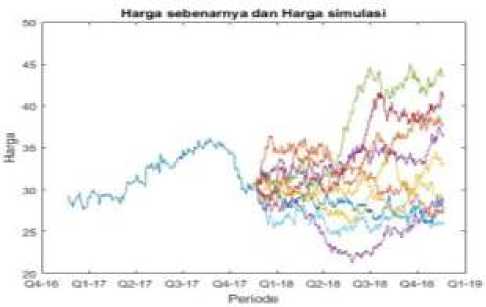
Gambar 3. Plot Harga Saham Sebenarnya dan Harga Saham Simulasi
Pada gambar 3 menunjukkan bahwa harga saham periode 2016 sampai dengan 2017 menunjukkan harga saham sebenarnya dan
harga saham pada periode 2017 sampai dengan 2018 merupakan prediksi harga saham dari hasil 10 kali simulasi.
Menghitung Nilai Opsi dari Masing-masing Simulasi Menggunakan Model Black-Scholes
Menentukan nilai opsi dari masing-masing simulasi dapat dilakukan menggunakan model Black-Scholes Pada model Black-Scholes terdapat lima input yang digunakan untuk menentukan nilai opsi yaitu, harga saham pada saat ini (S0) = 30.82, Strike Price (K) = 30 , waktu jatuh tempo ( T) = 1 tahun, tingkat suku bunga dalam satu tahun (r) = 4.5% dan volatilitas (σ) = volatilitas saham yang diperoleh dari masing-masing simulasi. Contoh hasil perhitungan nilai opsi dari 10 simulasi yang disajikan pada Tabel 1.
Tabel 1. Hasil Perhitungan Nilai Opsi dari Masing-masing Simulasi
|
Simulasi |
Opsi Call |
|
1 |
3.5822502 |
|
2 |
3.3359165 |
|
3 |
3.567483 |
|
4 |
3.4454045 |
|
5 |
3.4902379 |
|
6 |
3.4944578 |
|
7 |
3.4369244 |
|
8 |
3.5195746 |
|
9 |
3.5047733 |
|
10 |
3.3580474 |
Setelah opsi dari masing-masing simulasi diperoleh dapat ditentukan nilai rataan opsi dari masing-masing simulasi yaitu 3.4735. nilai tersebut kemudian dijadikan acuan untuk mengstimasi nilai Implied Volatility.
Menghitung Nilai Implied Volatility
Menghitung nilai Implied Volatility berdasarkan nilai rataan opsi yang diperoleh. Nilai opsi tersebut dijadikan acuan dengan membangkitkan nilai volatility yang memungkinkan (%). Nilai volatility kemudian diuji untuk mendapatkan nilai opsi yang mendekati nilai rataan opsi yang diperoleh dari hasil simulasi sebagai Implied Volatility.
Hasil perhitungan nilai Implied Volatility menggunakan simulasi Monte Carlo dengan alat bantu software MATLAB bisa dilihat pada Tabel 2.
Tabel 2. Hasil Perhitungan Nilai Implied Volatility
|
Jumlah Simulasi |
Rataan Opsi (USD) |
Implied Volatility (%) |
|
10 |
3.4735 |
18.94 |
|
20 |
3.4744 |
18.94 |
|
30 |
3.4601 |
18.82 |
|
40 |
3.4533 |
18.76 |
|
50 |
3.4662 |
18.86 |
|
60 |
3.4730 |
18.92 |
|
70 |
3.4731 |
18.92 |
|
80 |
3.4723 |
18.92 |
|
90 |
3.4701 |
18.9 |
|
100 |
3.4640 |
18.84 |
|
⸽ |
⸽ |
⸽ |
|
2000 |
3.4841 |
19.02 |
|
2100 |
3.4843 |
19.04 |
|
2200 |
3.4842 |
19.04 |
|
2300 |
3.4843 |
19.04 |
|
2400 |
3.4849 |
19.04 |
|
2500 |
3.4851 |
19.04 |
|
2600 |
3.4850 |
19.04 |
|
2700 |
3.4847 |
19.04 |
|
2800 |
3.4849 |
19.04 |
|
2900 |
3.4849 |
19.04 |
|
3000 |
3.4852 |
19.04 |
Berdasarkan output yang diperoleh pada Tabel 2 dapat dilihat bahwa nilai Implied Volatility yang sering diperoleh selama proses simulasi yaitu 19.04%. Dengan demikian dapat diestimasikan nilai Implied Volatility menggunakan simulasi Monte Carlo standar yaitu 19.04% dengan simulasi sebanyak 3000 kali.
Berdasarkan output yang diperoleh pada Tabel 2 dapat dilihat bahwa nilai Implied Volatility yang sering diperoleh selama proses simulasi yaitu 19.04%. Dengan demikian dapat diestimasikan nilai Implied Volatility menggunakan simulasi Monte Carlo standar yaitu 19.04% dengan simulasi sebanyak 3000 kali.
Simpulan
Berdasarkan hasil dan pembahasan yang telah diuraikan, estimasi nilai Implied Volatility saham menggunakan simulasi Monte Carlo pada data historis harga saham penutupan PT. Telekomunikasi Indonesia periode 22 November 2016 sampai 21 November 2017 dengan langkah awal yaitu menghitung tingkat pengembalian (return). Kemudian
mensimulasikan harga saham untuk mencari nilai opsi yang dijadikan acuan dengan menentukan nilai rataan opsi dari masing-masing simulasi. Sehingga dapat diestimasikan nilai Implied Volatility dengan melihat hasil output yang diperoleh selama proses simulasi sebanyak 3000 kali yaitu 19.04%. Semakin tinggi nilai Implied Volatility akan mengakibatkan harga opsi menjadi mahal karena Implied Volatility merupakan cara untuk mengukur harga opsi saham tanpa harus menganilis harga opsi saham sebenarnya.
Saran
Penulis menyadari bahwa dalam penelitian ini masih memiliki kekurangan. Hal tersebut dikarenakan estimasi nilai Implied Volatility masih menggunakan simulasi Monte Carlo yang standar. Adapun hal-hal yang disarankan peneliti untuk penelitian selanjutnya adalah mengembangkannya pada simulasi Monte Carlo dengan variance reduction untuk mengestimasi nilai Implied Volatility.
DAFTAR PUSTAKA
Brigham dan Houston, 2011. Essentials of
Financial Management.Edisi 11. Selemba empat,Jakarta.: s.n.
Changiagi, Andrea., 2000. Implied Volatility Estimation using Adjoint Monte Carlo Methods.
Dharmawan, K. & Widana, I. N., 2011.
Aplikasi Algoritma Biseksi dan Newton-Raphson dalam Menaksir Nilai Volatilitas Implied. Jurnal Matematika, Volume 2, p. 1.
Duan, J.C., 1995. The GARCH Option Pricing Model. Mathematical Finance, 5(1) 13-32.
Garman, Mark B & Klass, Michael J., 1980. On the Estimation of Security Price Volatilities from Historical Data. The Journal of Business, Vol. 53, No. 1, PP. 67-76.
Halim, A., 2005. Analisis Investasi. Jakarta: Salemba Empat.
Hull, J. C., 2009. Option, Futures, and Other Derivatives. 7th ed. New Jersey: Pearson Prentice Hall.
Indonesia, PT.TELKOM. 2017. Tentang Telkom dan Informasi Saham from http://www.telkom.co.id.
Lee, Roger. W., 2002. Implied Volatility:
Statics, Dynamics, and Probabilistic
Interpretation. Recant Advances in Applied Probability 2005, pp. 241-268.
Lya Aklimawati, T. W., 2013. Estimasi
Volatilitas Harga Kakao Menggunakan Model ARCH dan GARCH. PELITA PERKEBUNAN, Volume 29, p. 144.
Renault, E. & N, Touzi., 1996. Option Hedging and Implied Volatilities in a Stochastic Volatility Model. Mathematical Finance. 6, 279-302.
Schwert, 1992. Empirical Research in Capital Market. Mc Graw Hill.
Seydel, R., 2002. Tools For Computational Finance. jerman: Springer.
Tandelilin, E., 2010. Portofolio Investasi Teori dan Aplikasi. Yogyakarta: s.n
245
Discussion and feedback