PENENTUAN CADANGAN PREMI DENGAN METODE NEW JERSEY PADA ASURANSI JOINT LIFE

E-Jurnal Matematika Vol. 7(3), Agustus 2018, pp. 226-231

DOI: https://doi.org/10.24843/MTK.2018.v07.i03.p207

ISSN: 2303-1751

PENENTUAN CADANGAN PREMI DENGAN METODE NEW JERSEY PADA ASURANSI JOINT LIFE

Jenne Lali Tewo^1§, I Nyoman Widana², Tjokorda Bagus Oka³

¹Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email:Jenne2295@gmail.com] ²Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email:nwidana@yahoo.com] ³Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email:tjokordabagusoka@gmail.com]

^§Corresponding Author

ABSTRACT

Joint Life insurance is an insurance that covered two individuals in one policy. The purpose of this research is to determine and to compare the reserve value of Joint Life insurance using New Jersey method and Prospective method with and without New Jersey method. The method that used in this research are New Jersey method, the participants of this assurance is a couple of husband and wife between 45 and 40 years old with 30 years period, interest levels at 6,5%. The results of this represent reserve value with New Jersey method always smaller, and the reserve value in the 30 years period have the same result using New Jersey method and Prospective method.

Keywords: Joint Life Insurance, Premium Reserve, Vasicek, Prospective.

• 1.    PENDAHULUAN

Masyarakat mengalami suatu kejadian yang tidak terduga, kejadian tersebut seperti kehilangan harta benda, sakit, ataupun kecelakaan, Karena itu masyarakat perlu menyiapkan diri untuk mengatasi risiko yang tidak terduga tersebut. Salah satu cara untuk mengurangi risiko yang tidak pasti adalah dengan mengikuti asuransi (Sembiring, 1986).

Asuransi (insurance) “pertanggungan” dalam ketentuan pasal 1 UU no.2 tahun 1992 tentang usaha perasuransian, didefinisikan bahwa asuransi atau pertanggungan adalah perjanjian antar dua pihak atau lebih, dengan mana pihak penanggung mengikatkan diri kepada tertanggung, dengan menerima premi asuransi, untuk memberikan penggantian kepada tertanggung karena kerugian kerusakan atau kehilangan keuntungan yang diharapkan, atau tanggung jawab hukum kepada pihak ketiga yang mungkin akan diderita tertanggung, yang timbul dari suatu peristiwa yang tidak pasti, atau untuk memberikan suatu pembayaran yang didasarkan atas meninggal atau hidupnya

seseorang yang dipertanggungkan. (www.hukumonline.com)

Adapun berbagai jenis asuransi yaitu asuransi jiwa, asuransi pendidikan, asuransi kesehatan, dan lain sebagainya (Sembiring, 1986). Asuransi jiwa merupakan program yang memberikan perlindungan terhadap risiko, berkaitan dan meninggalnya seseorang yang dipertanggungkan ketika mengikuti asuransi. Asuransi jiwa berdasarkan jumlah tertanggung yang dapat dibagi menjadi dua yaitu: asuransi single life dan asuransi jiwa gabungan (joint life).

Asuransi joint life adalah asuransi yang menanggung dua jiwa atau lebih dalam satu polis asuransi. Dalam polis asuransi joint life perusahaan asuransi akan memberikan sejumlah uang yang disebut sebagai santunan atau uang pertanggungan kepada tertanggung dalam asuransi joint life. Sedangkan tertanggung juga mempunyai kewajiban terhadap perusahaan asuransi jiwa yaitu membayar sejumlah uang yang disebut premi. Premi yang terkumpul pada perusahaan asuransi jiwa yang akan dipakai oleh

perusahaan untuk membayar uang pertanggungan dan biaya administrasi. Selisih dari pendapatan yang diperoleh oleh perusahaan asuransi dari pembayaran premi dengan pengeluarannya disebut dengan cadangan.

Studi yang terkait tentang asuransi joint life telah dilakukan oleh Dewi (2016) yang menyatakan bahwa penentuan cadangan premi untuk asuransi joint life, hasil yang diperoleh berdasarkan formula cadangan premi tersebut serta untuk kasus usia awal peserta laki-laki 50 tahun dan perempuan 45 tahun dan lama pembayaran premi 10 tahun, diperoleh nilai cadangan premi akhir tahun ke-1 sampai akhir tahun ke-11 mengalami peningkatan setiap tahunnya, sedangkan nilai cadangan premi dari akhir tahun ke-12 dan seterusnya sampai seumur hidup mengalami penurunan. Demikian juga penelitian yang terkait dengan metode New Jersey telah dilakukan oleh Sari (2016) dalam penelitian yang menyatakan cadangan asuransi jiwa dwiguna semikontinu untuk usia pecahan dengan metode New Jersey. Menghasilkan nilai premi tahunan asuransi jiwa dwiguna semikontinu yang lebih besar, selanjutnya dengan besar premi tahunan yang sama pada akhir tahun ke-t untuk k <20 < m nilai cadangan yang dihasilkan dengan metode New Jersey. Hal ini dikarenakan adanya biaya tambahan yang diperhitungkan selama masa penyesuaian dalam metode New Jersey. Namun pada akhir tahun masa pertanggungan nilai cadangan yang diperoleh sama.

Iswatika (2014) menyatakan bahwa menentukan besar cadangan disesuaikan dengan metode New Jersey pada asuransi jiwa endowment. Hasil yang diperoleh adalah sumber dana tambahan untuk menutup biaya awal tahun dapat diperoleh dengan menyesuaikan cadangan premi, dengan menggunakan metode New Jersey. Pada asuransi jiwa endowment 30 tahun, cadangan pada akhir tahun ke-t berdasarkan perhitungan cadangan prospektif dan retrospektif menghasilkan nilai cadangan yang hampir sama dan pada akhir waktu polis, nilai cadangan disesuaikan dengan metode New Jersey hampir sama dengan nilai santunan yang diberikan.

Metode New Jersey mempunyai kelebihan yang sangat berguna dalam pembuatan tabel cadangan (Destriani dkk, 2014), karena perhitungan nilai cadangan yang digunakan setiap tahun secara berurutan. Perhitungan nilai cadangan menggunakan metode New Jersey juga bermanfaat untuk perusahaan dalam menutupi kekurangan biaya pada tahun pertama polis, kemudian akan dibayar kembali dari premi tahun-tahun berikutnya. Sehingga dalam perhitungan joint life lebih merupakan asuransi jiwa bersama yang pembayaran preminya sampai kematian pertama dari pesertanya. Pada asuransi jiwa bersama joint life premi yang dibayarkan oleh peserta asuransi akan berakhir atau berhenti jika salah satu dari peserta asuransi tersebut meninggal dan kemudian ahli waris mendapat santunan dari perusahaan asuransi. Pada penelitian ini akan dicari menghitung besar cadangan premi asuransi joint life dan menghitung besarnya cadangan asuransi joint life jika menggunakan metode New Jersey.

Selanjutnya dibahas komponen-komponen yang diperlukan dalam penentuan cadangan premi dengan metode New Jersey pada asuransi joint life yaitu:

Variabel random sisa usia adalah usia kematian seseorang yang berusia x dan sisa usia dari seseorang yang berusia x tahun merupakan suatu peubah acak kontinu. Cara perhitungan variabel random sisa usia yang digunakan yaitu (Bowers et al, 1997):

tPx = 1- tPx =P [ Tx>t ] , t ≥ 0

Tabel mortalitas adalah rata-rata nilai kematian dalam setiap tahunnya dalam satu kelompok orang tertentu. Persamaan yang digunakan untuk melengkapi nilai tabel mortalitas yaitu:

Fungsi gabungan dari orang yang berusia x dan y tahun sehingga diperoleh sebagai berikut:

^xy lχ × Iy

Peluang orang yang berusia x dan y tahun akan tetap hidup selama 1 tahun sehingga diperoleh sebagai berikut:

⅛+ι ⁱy+ι ⅛y+ι

Pxy =Px×Py = —×V =⅛

Peluang orang yang berusia x dan y tahun akan tetap hidup selama n tahun dapat dirumuskan sebagai berikut:

n = ^lxm n Pxy = ^Lxy

Peluang orang yang berusia x dan y tahun meninggal dalam jangka waktu 1 tahun maka diperoleh sebagai berikut:

_ lχy~lχy+ι Qxy = ^Lxy

Tabel komutasi adalah tabel yang perhitungannya memiliki hubungan erat dengan tabel mortalitas. Cara perhitungan tabel komutasi yang digunakan (Futami, 1993): N_xy merupakan total penjumlahan

^xy=^Dx+ly+l ⁺ ^x+l ,y+i+⋯

Fungsi v sebagai nilai sekarang tingkat bunga

Nilai Tunai manfaat merupakan uang pertanggungan yang diperoleh dari pihak tertanggung pada saat melalukan klaim. Persamaan yang digunakan untuk menghitung nilai tunai manfaat yaitu:

n-l

^xy:.= E(Z)=∑ ^vk+l k | Qxy k=0

Anuitas hidup berjangka adalah suatu rangkaian pembayaran yang dilakukan selama jangka waktu tertentu. Persamaan yang digunakan untuk menghitung anuitas yaitu: n-l

a • xy : n˥ =∑V^t tPxy

t=0

Menurut (Larson dan Gaunmnitz, 1951), Penentuan cadangan disesuaikan dengan persamaan umum untuk cadangan dua orang atau peserta yang digunakan yaitu:

tV⅛y^m = ^Ax+t,y+t,:n-t\   pxy:n\^ax+t,y+t:n-t

• 2.    METODE PENELITIAN

Jenis penelitian ini menggunakan data sekunder, data sekunder merupakan sumber data yang diperoleh peneliti secara tidak langsung melalui media perantara. Pengolahan data pada penelitian ini menggunakan alat bantu software

Microsoft Excell. Pada perhitungan cadangan premi menggunakan langkah-langkah sebagai berikut:

• a. Melengkapi Tabel Mortalitas Indonesia 2011 b. Menghitung besar nilai Tabel Komutasi

• c.    Menghitung besar premi joint life, yaitu: (a) menghitung nilai tunai manfaat; (b) menghitung anuitas awal nilai sekarang joint life.

• d.    Mengkontruksi rumus untuk menentukan cadangan asuransi joint life dengan menggunakan metode new jersey.

• e.    Menghitung cadangan premi asuransi joint life menggunakan metode new jersey.

• f.    Membandingkan besar cadangan premi joint life dengan dan tanpa metode new jersey.

• g.    Menyimpulkan atau interpretasi dari hasil yang diperoleh.

• 3. HASIL DAN PEMBAHASAN

Dalam melengkapi tabel perhitungan berdasarkan Tabel Mortalitas Indonesia 2011 akan dihitung nilai P_y dan P_x menggunakan persamaan yang ditulis sebagai berikut:

Px=1-^Qx

Langkah selanjutnya membuat tabel komutasi. Pada pembuatan tabeli komutasi dilakukan perhitungan nilai v dan nilai-nilai komutasi, dengan menggunakan tingkat suku bunga konstan i=6,5%. Perhitungannya adalah:

• 1.    Perhitungan nilai v adalah fungsi nilai v sebagai nilai sekarang tingkat bunga

l

V = — l + l

• 2.    Perhitungan nilai ^x adalah menentukan banyaknya orang yang meninggal antara usia x tahun

D_x = V^xI_x

• 3.    Perhitungan nilai   N_x   adalah total

penjumlahan dari Dx

^Nx = Dx ^{+ D}x+l ^{+ D}x+2+⋯

• 4.    Perhitungan nilai Dy adalah menentukan banyaknya orang yang meninggal antara usia y tahun

Dy = V^yIy

• 5.    Perhitungan nilai   Ny   adalah total

penjumlahan dari Dy

Ny = Dy + ^Dy+l + ^Dy+2 +⋯

• 6.    Perhitungan nilai D_xy adalah menentukan banyaknya orang yang meninggal antara usia x tahun sampai x + y tahun sehingga dapat dihitung sebagai berikut:

D_xy = v^2(^x+y')l_xy

• 7.    Perhitungan nilai N_xy adalah menentukan penjumlahan dari D_xy sehingga diperoleh sebagai berikut:

^Nxy = ^Dx+1,y+1 ^{+ D}x+2,y+2 + "'

akan dihitung nilai tunai manfaat untuk pihak tertanggung yang berusia x=45 tahun dan y=40 tahun dan jangka waktu pertanggungan selama 30 tahun, diperoleh:

^45,40:30= ∑fc=0 $^fc+1 fc∣Q45,40

=0,938¹(1 - 0,996) + 0,938²(0,996 -0,991) + 0,938³(0,991 - 0,986) + +0,9 38³⁰(0,5 1 5 - 0,481)

= 0,247529589

untuk perhitungan tahun selanjutnya dapat digunakan perhitungan seperti ditas, yaitu:

A¹    =V0 r⁰⁺¹

^74,69:1  ∑k=0 $

= V⁰⁺¹(0P74,₆8^-1+1P74,68)

=0.93897¹(1 -0.870697)

=0.121411

Kemudian dihitung anuitas awal nilai sekarang

joint life untuk pihak tertanggung yang berusia x=45 tahun dan y=40 tahun dan jangka waktu

pertanggungan selama 30 tahun, diperoleh:

29

$45,40:301

=∑

t=0

V°_θP45,40

= 0.938⁰(1.000)+(0.995)+0.938² (0.990)

+0.938³(0.985)+.+0.938²⁹(0.515)

=12.32893828

untuk perhitungan tahun selanjutnya dapat digunakan perhitungan seperti ditas, yaitu:

0

_a             t „  _ „0 „

$73,68:21 = ∑ $ tPxy = $ oP73,68

t=0

= 0.938⁰(1.000) = 1

Selanjutnya, yaitu mengkontruksi rumus untuk menentukan cadangan asuransi joint life jika menggunakan metode new jersey. Adapun rincian kontrak dalam program asuransi adalah sebagai berikut, pihak tertanggung berusia x dan y tahun dengan jangka waktu pertanggungan selama n tahun. Apabila kedua peserta asuransi tetap hidup sampai kontrak asuransi berakhir maka peserta asuransi joint life diberikan uang

sejumlah Rp.1 dan kontrak asuransi berakhir. Apabila salah satu peserta asuransi joint life meninggal dunia sebelum masa kontrak berakhir, misalkan x meninggal, maka pemabayaran premi dihentikan dan rincian untuk pembayaran uang pertanggungan adalah sebagai berikut: apabila pasangan y tetap hidup pada akhir kontrak maka y akan diberikan uang pertanggungan sebesar Rp. 1 setiap tahunnya selama seumur hidup. Begitu juga sebaliknya, apabila y meninggal maka x diberikan uang pertanggungan sebesar RP. 1 setiap tahunnya selama seumur hidup. Namun apabila pasangannya juga meninggal sebelum masa kontrak berakhir maka tidak ada pembayaran uang pertanggungan. Berdasarkan rincian kotrak tersebut, maka pada persamaan (10) akan dikontruksi, sehingga diperoleh rumus untuk perhitungan cadangan asuransi joint life menggunakan metode new jersey:

⅛i7 = _c^x+t,y+t:n-t| ^- (β^{1 -} ⅛P‰,y+_t^0-_t∣ t                 ⁱ

• -P$x+t,y+t:_n-t|)                   (19)

Sebelum menentukan besar nilai cadangan, terlebih dahulu dihitung besar nilai premi joint life, diperoleh:

P    _^¾yn1

^px,y:n1= _& ^αX∑∏ι

Pas 40 sot= ^⁴⁵,⁴⁰:³⁰¹= -⁰²³⁸ = 0.01911132 ^45,40:301  «45,40:301  12.477

Setelah diperoleh besar nilai premi, maka dapat ditentukan besar nilai cadangan asuransi joint life menggunakan persamaan (19):

Berdasarkan persyaratan dari metode new jersey bahwa dalam menghitung besar nilai cadangan dimulai dari tahun ke-2 karena pada tahun pertama nilai cadangan harus nol.

Cadangan premi tahun ke-2:

• ²^45,40:3011 = ^45+2,40+1:30-2 |    ⁽^      ^P 45,40:30 | )

β^T 1   ~    - P T T T

45+2,40+2:20-2|45,40:30|

$—-----------T )

45+2,40+2:30-2|⁷

=1× 0.264072402-(0.004768820.01911132) × 10․41655244 -0․01911132× 12․05789065 =0․1830504

Cadangan premi tahun ke-3:

³145,40:30V = ^45+3,40+1:30-3 I    ⁽^     ^P 45,40:30 ¹ )

$ _ _--——- P tr—r

45+3,40+3:20-3|45,40:30|

^a-------------------1 )

4 5+3,4 O+3: 3 O - 3 ∣ ^j

=1 ×0.277599909-(0.00476882-

0.01911132) × 10.07937682 -

0.01911132× 11.83624765

= 0.19597722

berlaku juga untuk perhitungan selanjutnya sampai pada besar nilai cadangan ke-19, diperoleh:

Cadangan premi Tahun ke -19:

19^14 S ,4 O : 3 O 1 ⁴ = ^4 5 ₊ 49,4 0 + 1 : 3 O - 19 ∣    ⁽^      ^P4 S ,4 O : 3 O ∣ )

β^---r — P _—;—r

45 + 19,4O+19:2O-19|45,4O:3O|

a—-------------r)

45 + 19,4O+19:3O-19|⁷

=1× 0.569136175-(0.00476882

0.01911132) × 1.913276139 —

0.01911132× 7.059538055

= 0.4616641

Selanjutnya, membandingkan besar cadangan premi asuransi joint life menggunakan metode prospektif dengan dan tanpa metode new jersey. Berdasarkan persamaan (10) maka dihitung cadangan premi joint life, diperoleh:

Cadangan Premi Tahun Ke-1:

1^45,4O:3O | = ^46,41:29 ^{- Pa}46,41:29|

=0.247529589-0.01911132 × 12.32893828 = 0.2169711

Cadangan Premi Tahun Ke-2:

2^45,4O:3O | = ^4742: 28 ^{- Pa}47,42:28| =0.264072402-0.01911132 × 12.05789065

=0.2341858

• 4.    SIMPULAN DAN SARAN

• A.    Simpulan Penelitian

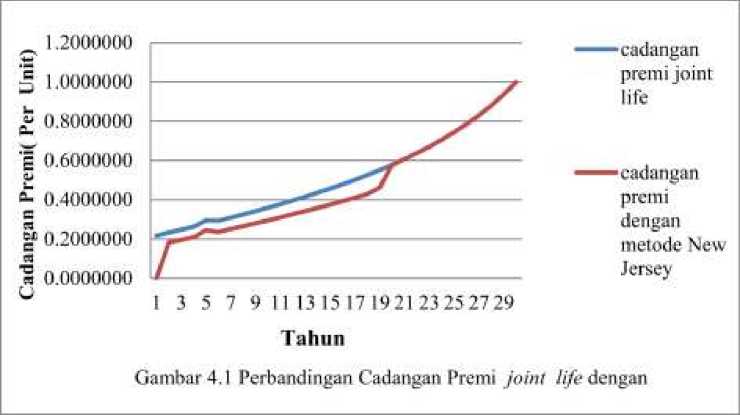
Besar cadangan premi asuransi Joint life yang dihitung dengan menggunakan Metode New Jersey selalu lebih kecil sebelum tahun ke-19 dan bernilai sama pada tahun ke-20 sampai jatuh tempo tahun ke-30 dengan besar cadangan premi asiransi cara prosfektif.

• B.    Saran

Pada penelitian ini menghitung nilai cadangan premi dengan menggunakan suku  bunga

konstan. Untuk penelitian selanjutnya dapatmenggunakan metode kanada, atau jenis asuransi lainnya dan suku bunga tidak konstan. Cadangan Premi Tahun Ke-3:

3^O1,40:14 | = A04,41:14 ^{- P}^io4,oH:14|

=0.277599909-0.01911132× 11.83624765 =0.9364885

Berlaku juga untuk seterusnya, sampai pada perhitungan cadangan premi untuk tahun ke-30, diperoleh:

Cadangan Pada Tahun Ke-30:

3O^45,4O:3O | = ^46,41:O ^{- Pa}46,41:O|

=1

Perbandingan Cadangan Premi joint life menggunakan metode prospektif dan metode New Jersey

DAFTAR PUSTAKA

Bowers NL, Gerber HU, Hickman JC, Jones DA, dan Nesbitt CJ. 1997. Actuarial Mathematics,  2^nd ed. Scaumburg: The

Society of Actuaries.

Destriani, Satyahadewi, N. & Mara, M.N., 2014. Penentuan Nilai Cadangan Prospektif pada Asuransi Jiwa Seumur Hidup Menggunakan Metode New Jersey. Buletin Ilmiah Mat.Stat dan Terapannya (BIMASTER), 03, pp.7-12.

Dewi, NL.P.R., 2016. Penentuan Cadangan Premi Untuk Asuransi Joint Life. Skripsi, S1 Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Udayana, Bali.

Futami, T., 1994. Matematika Asuransi Jiwa, Bagian I. Tokyo: Oriental Life Insurance Cultural Development Center. Terjemah dari: Seime Hoken Sugaku Gekan (“ 92 Revision).

Iswatika, R. F., 2014. Penentuan Cadangan

Disesuaikan pada Asuransi Jiwa Endowment, Skripsi, S1 Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Brawijaya, Malang.

Larson R.E. dan Gaumnitz, E.A., 1951. Life Insurance Mathematics, John Willey & Sons, Inc., New York.

Sari, Retno., 2016. Cadangan Asuransi Jiwa Dwiguna Semikontinu Untuk Usia Pecahan Dengan Metode New Jersey, Artikel, S1 Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Riau. JOM vol. 1 No.2.

Sembiring, R.1986. Buku Materi Pokok Asuransi I Modul 1-5. Jakarta:Karunika

231