E-Jurnal Matematika Vol. 7(3), Agustus 2018, pp. 203-210

DOI: https://doi.org/10.24843/MTK.2018.v07.i03.p204

ISSN: 2303-1751

MENGKLASIFIKASIKAN DESA PERKOTAAN DAN DESA PERDESAAN DI KABUPATEN KLUNGKUNG MENGGUNAKAN METODE MAMDANI

Ni Kadek Sumarwati1§, G. K. Gandhiadi2, Tjokorda Bagus Oka3

§Corresponding Author

ABSTRACT

According to Bureau of Statistic, village can be classified into urban and rural village. This classification is useful for planning development, such as security, health, and agriculture plans which have the roles of rural urban linkages. This classification also useful for divide a village into villages. In this research the villages in Klungkung Regency will be classified into urban and rural villages using Mamdani method. The result of classification using Mamdani method is 52 villages classified into urban village and seven villages classified into rural village which has an accuracy of 93% between the Mamdani method output with the original data in 59 villages in Klungkung Regency.

Keywords: fuzzy logic, Mamdani method, classification, urban, rural, accuracy

  • 1.    PENDAHULUAN

Kabupaten Klungkung merupakan kabupaten yang luasnya terkecil kedua setelah Kota Denpasar dari sembilan kabupaten dan kota di Bali dengan luas wilayah 315 km2 (Badan Pusat Statistik Kabupaten Klungkung, 2016). Secara administratif Kabupaten Klungkung terdiri dari empat kecamatan dan 59 desa/kelurahan. Setiap desa mempunyai ciri dan tipologi lingkungan, kondisi ekonomi, akses fasilitas umum yang berbeda-beda, dan akan terus berubah seiring dengan kemajuan tingkat pembangunan di suatu desa. Berdasarkan peraturan Kepala Badan Pusat Statistik Nomor 37 Tahun 2010 tentang klasifikasi perkotaan dan perdesaan di Indonesia maka desa/kelurahan dapat dikategorikan menjadi wilayah perkotaan dan wilayah perdesaan berdasarkan nilai/skor dari indikator yang telah ditetapkan oleh Badan Pusat Statistik. Indikator yang dimaksud adalah kepadatan penduduk (jiwa/km2), persentase rumah tangga pertanian (%), dan akses fasilitas umum (Badan Pusat Statistik, 2010).

Skor atau nilai dalam klasifikasi ditentukan dengan batas minimal 10 maka desa tersebut termasuk perkotaan sedangkan apabila skor kurang dari 10 maka desa berstatus perdesaan (Badan Pusat Statistik, 2010). Adanya perubahan kecil nilai pada suatu indikator mengakibatkan perbedaan skor yang dapat mengubah status suatu desa. Hal tersebut sangat kaku, sehingga himpunan fuzzy akan digunakan dalam penelitian ini yang dirasa mampu untuk mengantisipasi hal tersebut. Salah satu metode yang dapat digunakan dalam pengaplikasian logika fuzzy untuk mengklasifikasikan desa perkotaan dan desa perdesaan adalah metode Mamdani.

Metode Mamdani pertama kali diperkenalkan oleh Ebrahim Mamdani pada tahun 1975. Metode Mamdani juga sering disebut metode Min-Max, yaitu mencari nilai minimum dari setiap aturan dan nilai maksimum dari gabungan konsekuensi setiap aturan (Kusumadewi & Purnomo, 2010). Metode

Mamdani memiliki kelebihan yakni, lebih intuitif, diterima oleh banyak pihak, cocok digunakan apabila input diterima dari manusia bukan mesin.

Beberapa penelitian tentang logika fuzzy metode Mamdani yaitu penelitian oleh Ayuningtiyas, dkk. (2007) yang memperoleh hasil akurat dalam pengambilan keputusan mengenai keadaan balita di suatu daerah, penelitian oleh Arifin, dkk. (2015) yang bertujuan untuk mendeteksi kerentanan banjir di Semarang Utara menggunakan lima defuzifikasi memperoleh hasil pengujian dengan kesimpulan yang sama dari dua contoh kasus, dan penelitian oleh Muthohar, dkk. (2016) yang bertujuan untuk mengevaluasi kinerja pelayanan perawat berdasarkan tangibility, reliability, responsiveness, assurance, dan empathy memperoleh hasil yang sesuai antara keluaran sistem fuzzy dengan keluaran yang diharapkan.

Pada penelitian ini logika fuzzy metode Mamdani digunakan dalam mengklasifikasikan desa perkotaan dan desa perdesaan di Kabupaten Klungkung. Tujuan klasifikasi ini adalah untuk mengetahui klasifikasi dan ketepatan hasil klasifikasi desa perkotaan dan desa perdesaan di Kabupaten Klungkung menggunakan metode Mamdani.

  • 2.    METODE PENELITIAN

Data yang digunakan dalam penelitian ini adalah data sekunder yang diperoleh dari Badan Pusat Statistik Kabupaten Klungkung. Data tersebut merupakan data hasil pencatatan setiap kecamatan dan desa di Kabupaten Klungkung tahun 2016. Langkah-langkah yang dilakukan dalam penelitian ini adalah sebagai berikut:

  • 1.    Menentukan variabel input dan variabel output

Pada penelitian ini terdapat tiga variabel input yaitu Kepadatan Penduduk (KPD), Persentase Rumah Tangga Pertanian (PRT), dan Akses Fasilitas Umum (AFU) dan satu variabel output yaitu Status Desa (SD).

  • 2.    Menentukan himpunan universal dan himpunan fuzzy

Himpunan universal untuk variabel input yaitu: KPD=[0, 20000], PRT=[0, 100], dan

AFU=[0,  10] serta variabel output Status

Desa=[0, 20]. Sedangkan himpunan fuzzy untuk masing-masing variabel input akan dibagi menjadi tiga himpunan fuzzy dan dua himpunan fuzzy untuk variabel output. Nilai himpunan universal untuk variabel input dan output ditentukan oleh peneliti berdasarkan nilai minimum, maksimum, dan median data klasifikasi desa.

  • 3.    Menentukan aturan fuzzy

Banyaknya aturan fuzzy yang dapat terbentuk diperoleh dari hasil kali jumlah masing-masing himpunan fuzzy pada variabel input (Bojadziev & Bojadziev, 2007).

  • 4.    Aplikasi fungsi implikasi Min

Pada langkah ini akan dicari output untuk setiap aturan dengan menggunakan fungsi implikasi min pada persamaan (1).

μ a ∧μe(z) = a∧μc(z) = min(u a(z) =

a ,μc(z))                                    (1)

dengan,

a = μA(x)∧μB(y) = min(μX%),μg(y));

x = x0 dan y = y0

Keterangan:

μ a ∧μs (z) = daerah hasil fungsi implikasi min a = nilai keanggotaan hasil operasi himpunan fuzzy A dan B

μ a(x) = derajat keanggotaan himpunan fuzzy A μ S (y) = derajat keanggotaan himpunan fuzzy B μc(z) = derajat keanggotaan konsekuen pada himpunan C

  • 5.    Melakukan agregasi

Agregasi metode max akan digunakan dalam penelitian ini yaitu dengan mengambil nilai maksimum untuk setiap output himpunan fuzzy dari hasil aplikasi fungsi implikasi menggunakan persamaan (2) :

μsf (Xi) = max(μs f(xi),μkf(xi))           (2)

dengan μs f(x i) adalah nilai keanggotaan solusi fuzzy sampai aturan ke-i dan μf((xi) = nilai keanggotaan konsekuen aturan ke-i.

  • 6.    Melakukan defuzzifikasi

Defuzzifikasi pada penelitian ini menggunakan metode centroid untuk mendapatkan nilai variabel solusi dari suatu daerah konsekuen dengan cara mengambil titik pusat daerah fuzzy menggunakan persamaan:

∗∫; ^U (z) dz

∫ . <“ (z) dz

Keterangan:

Z ∗ = nilai hasil penegasan (defuzzifikasi)

Z = nilai domain ke-j

Vt- (z) = derajat keanggotaan z

  • 7.    Hasil klasifikasi setiap desa

Hasil klasifikasi setiap desa diperoleh dengan mensubstitusikan nilai defuzzifikasi ke dalam fungsi keanggotaan pada masing-masing himpunan fuzzy variabel output dan menentukan klasifikasi dari nilai yang diperoleh.

  • 8.    Uji ketepatan hasil klasifikasi

Pada langkah terakhir akan dihitung ketepatan hasil klasifikasi dengan menggunakan confusion matrix untuk membandingkan hasil klasifikasi metode Mamdani dengan data asli.

sebagai berikut.

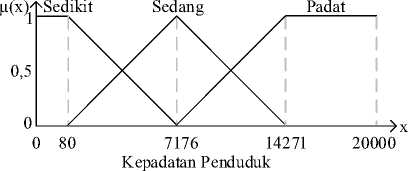
Gambar 1. Fungsi Keanggotaan Variabel Kepadatan Penduduk

Fungsi keanggotaan variabel kepadatan penduduk:

1, X<80;

7176 - X

  • -Sedikit (X)= 5         ,80≤X ≤ 7176;

7096

0, X > 7176.

MSedang (X)= 14271 -


c-80

7096,80≤1<7176;


7095


, 7176≤X ≤ 14271;


0, X > 14271 atau x<80.

0, X < 7176;

- 7176

M-Padat (X)= j  7095 ,7176≤X ≤ 14271;

1, X > 14271.

3. HASIL DAN PEMBAHASAN

Berikut adalah perancangan himpunan fuzzy untuk menentukan status desa.


0     5      10     15    20             100

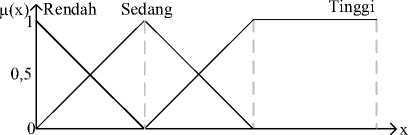
Persentase Rumah Tangga Pertanian

Gambar 2. Fungsi Keanggotaan Variabel Persentase Rumah Tangga Pertanian


Tabel 1. Tabel Himpunan Fuzzy

Variabel

Himpunan

Domain

Fungsi Keanggotaan

KPD

Sedikit

[0, 7176)

Bahu Kiri

Sedang

(80, 14271)

Segitiga

Padat

(7176, 20000]

Bahu Kanan

PRT

Rendah

[0, 10)

Linear Turun

Sedang

(0, 20)

Segitiga

Tinggi

(10, 100]

Bahu Kanan

AFU

Rendah

[0, 4)

Linear Turun

Sedang

(0, 7)

Segitiga

Tinggi

(4, 10]

Bahu Kanan

SD

Desa

Perdesaan

[0, 15)

Bahu Kiri

Desa

Perkotaan

(5, 20]

Bahu Kanan


Fungsi keanggotaan variabel persentase rumah tangga pertanian:

1, X<0;

10-X

MRendah (X)= {  10  ,0≤X≤10;

0, X>10.


0, X<0atau x>20;


x-0

,0≤x<10;


20-x

10


,10≤x≤20.


Berdasarkan Tabel 1, fungsi keanggotaan dari masing-masing variabel direpresentasikan


0, x<10;

-10

Mτtnggi (X)= j  10 ,10≤X≤20;

1, X>20․



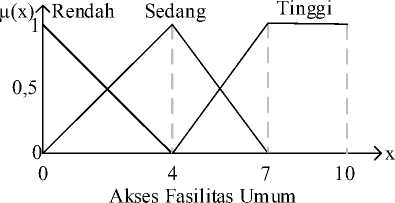
Gambar 3. Fungsi Keanggotaan Variabel Akses Fasilitas Umum


Fungsi keanggotaan variabel akses fasilitas umum:

1,x < 0; 4 —

^R e n d a h (x)   j ^ , 0 ≤ X ≤ 4;

0,X>4.


0, x


< 0 atau > > 7;


-


^Sedang (x) =


4

7 —


0 - ,0 ≤


x <4;


3  ,4 ≤


x ≤ 7.


0,X < 4;

— 4

^T Inggi O'-)    j j , 4 ≤ X ≤7;

1,x > 7.



Gambar 4. Fungsi Keanggotaan Variabel Status Desa


Fungsi keanggotaan variabel status desa:


l^Desa Perdesaan


(Z)


{—

10


1,z < 5;

—, 5 ≤ z ≤ 15;

0,z > 15.


^Desa Perleotaan


(z)


=!:


—


10


0, z < 5;

5

—, 5 ≤ z ≤ 15;


1, z > 15.


Menentukan Aturan Fuzzy

Banyak aturan fuzzy yang terbentuk dari tiga variabel input dengan masing-masing tiga himpunan fuzzy adalah 33 = 27 aturan fuzzy.


Tabel 2. Aturan Fuzzy

R

KPD

PRT

AFU

SD

1

Sedikit

Sedang

Rendah

Desa Perdesaan

2

Sedikit

Tinggi

Rendah

Desa Perdesaan

3

Sedang

Tinggi

Rendah

Desa Perdesaan

4

Padat

Tinggi

Rendah

Desa Perdesaan

5

Sedikit

Rendah

Rendah

Desa Perkotaan

6

Sedikit

Rendah

Sedang

Desa Perkotaan

7

Sedikit

Rendah

Tinggi

Desa Perkotaan

8

Sedikit

Sedang

Sedang

Desa Perkotaan

9

Sedikit

Sedang

Tinggi

Desa Perkotaan

10

Sedikit

Tinggi

Sedang

Desa Perkotaan

11

Sedikit

Tinggi

Tinggi

Desa Perkotaan

12

Sedang

Rendah

Rendah

Desa Perkotaan

13

Sedang

Rendah

Sedang

Desa Perkotaan

14

Sedang

Rendah

Tinggi

Desa Perkotaan

15

Sedang

Sedang

Rendah

Desa Perkotaan

16

Sedang

Sedang

Sedang

Desa Perkotaan

17

Sedang

Sedang

Tinggi

Desa Perkotaan

18

Sedang

Tinggi

Sedang

Desa Perkotaan

19

Sedang

Tinggi

Tinggi

Desa Perkotaan

20

Padat

Rendah

Rendah

Desa Perkotaan

21

Padat

Rendah

Sedang

Desa Perkotaan

22

Padat

Rendah

Tinggi

Desa Perkotaan

23

Padat

Sedang

Rendah

Desa Perkotaan

24

Padat

Sedang

Sedang

Desa Perkotaan

25

Padat

Sedang

Tinggi

Desa Perkotaan

26

Padat

Tinggi

Sedang

Desa Perkotaan

27

Padat

Tinggi

Tinggi

Desa Perkotaan


Aplikasi Fungsi Implikasi Min

Fungsi implikasi yang akan digunakan adalah fungsi implikasi min yaitu dengan mengambil nilai keanggotaan terkecil untuk setiap aturan fuzzy. Misalkan diambil data desa 1 yaitu Desa Sakti dalam Tabel 3.


Tabel 3. Data Desa 1

Variabel

Data Desa 1

KPD

250,23

PRT

8,84

AFU

1

SD

Desa Perdesaan


Selanjutnya data pada Tabel 3 diubah dalam himpunan fuzzy dengan mencari derajat keanggotaan menggunakan fungsi pendekatan masing-masing himpunan yang disajikan dalam Tabel 4.


Tabel 4. Derajat Keanggotaan Desa 1

Variabel

Input

Himpunan Fuzzy

Derajat

Keanggotaan

KPD

Sedikit

0,98

Sedang

0,02

Padat

0

PRT

Rendah

0,12

Sedang

0,88

Tinggi

0

AFU

Rendah

0,75

Sedang

0,25

Tinggi

0

Tabel 5. Fungsi Keanggotaan Hasil Implikasi Min Desa 1

R

Fungsi Keanggotaan

1

0, Z < 7,5;

z A J 15-Z

Ij-Rl (Z)= {  10 ,7,5≤Z≤15;

0, Z>15․

2

Ij R2 (Z)={0,∀Z∈R2 ․

3

μκ3 (Z)={0,∀Z∈R3 ․

27

llR27 (Z)={0,∀Z∈R27․

Selanjutnya dilakukan operasi komposisi pada setiap rule, derajat keanggotaan hasil operasi komposisi kemudian digunakan untuk melakukan implikasi min untuk memperoleh solusi setiap rule. Hasil operasi komposisi desa 1 untuk rule 1 sampai rule 27:

Ct1 =min(0,98;0,88; 0,75) =0,75;

«2 =min(0,98;0;0,75) =0;

Ct3 =min(0,02;0;0,75) =0;

a27 =min(0; 0; 0) =0․

Berdasarkan hasil operasi komposisi di atas, maka fungsi implikasi min desa 1 untuk rule 1 sampai rule 27 sebagai berikut:

I1Rl (Z)=Ct1 ∧ I1Desa Perdesaan (Z)

= min(0,75, IA-Desa Perdesaan (Z));

llR2 (Z)=a2 ∧ IA-Desa Perdesaan (Z)

= min(0, IA-Desa Perdesaan (Z));

llR3 (Z)=«3 ∧ I1Desa Perdesaan (Z)

= min(0, I1-Desa Perdesaan (Z));

llR27(Z)=a27 ∧ IADesa Perkotaan (Z)

= min(0, IADesa Perkotaan (Z))․

Sehingga diperoleh fungsi keanggotaan hasil implikasi min untuk setiap rule pada desa 1 yang disajikan pada Tabel 5.

Berdasarkan fungsi implikasi pada Tabel 5 diketahui bahwa dari 27 rule pada desa 1 yang memiliki daerah hasil implikasi selain 0 yaitu rule: 1, 5, 6, 8, 12, 13, 15, dan 16.

Gambar 5 berikut merupakan daerah hasil implikasi desa 1 untuk rule 1.

R1


0,5


Sedikit

0,5

0

µ0(,x9)81

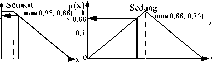
Rendah

x (%)

µ(x)

0,75

0,5

0 80 250,23    7176    0 2 4 6 8 8,84 10 12 14 16 18 20

Kepadatan Penduduk Persentase Rumah Tangga Pertanian


µ(x) Desa Perdesaan esa Perdesaan(z))1 --> 0,75

z

Status Desa


0 —1-----^*x0

0  1    2   3   4

Akses Fasilitas Umum

Gambar 5. Daerah Hasil Implikasi Rule 1

Melakukan Agregasi

Solusi himpunan fuzzy diperoleh dengan cara mengambil nilai maksimum output aturan hasil aplikasi fungsi implikasi min, kemudian menggunakannya untuk memodifikasi daerah fuzzy, dan mengaplikasikannya ke output dengan menggunakan operator OR (union). Hasil komposisi aturan max untuk setiap himpunan fuzzy variabel output sebagai berikut:

IADesa Perdesaan (Z)

= max{P-Rl (Z), ∣Ar2 (Z), ∣Ar3 (Z), ∣Ar4 (Z)}

=    (Z)

IADesa Perkotaan (Z)

= max{IArs (z), ∣Ar6 (Z), llR7 (Z),…,llR27 (Z)}

=    (Z)

Pada persamaan di atas diketahui bahwa fungsi maksimum untuk output desa perdesaan adalah rule 1 dan fungsi maksimum untuk output desa perkotaan adalah rule 8, yang telah mewakili nilai pada masing-masing himpunan fuzzy variabel output hasil implikasi setiap rule. Persamaan agregasi untuk desa 1 sebagai berikut:

IAsf (Z)


= max{ IADesa Perdesaan (Z), IADesa Perkotaan (Z)}


= max{IAr-L (z), I1RS (Z)}


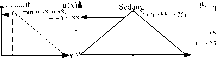
Daerah hasil agregasi desa 1 dapat dilihat pada gambar berikut:


= — 7 5z 2

10 7,


3l12,5


R1


0


µ(x) Sedikit 0,981

0,5

,,

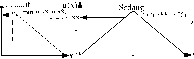
Kepadatan Penduduk Persentase Rumah Tangga Pertanian Akses Fasilitas Umum

0 80 250,23     7176    0 2 4 6 8 8,84 10 12 14 16 18 20


µ(x) Rendah

0,75 0,5

a Perdesaan(z)) 0,5

esa P

Sedang

x (%)

0           0   1    2   3   4


µ(x) Desa Perdesaan


R8


µ(x)

µ(x) Sedikit 0,981

0,5

,,

Kepadatan Penduduk Persentase Rumah Tangga Pertanian

0 80 250,23

0,25

x (%) 0

7176    0 2 4 6 8 8,84 10 12 14 16 18 20        0


0z

0 2  4  6 8 10 12 14 15

Status Desa

µ(x)

in(0,25, µDesa Perkotaan(z))

0,5

Desa Perkotaan

0   2   4  6   8   10

Status Desa


z


—


3


j7, 5


= 23,958;


r20

M3 = I   (0,25)z dz = 0,125z2 ]2 θ 5

2,5                                                     ,

= 30,46875.


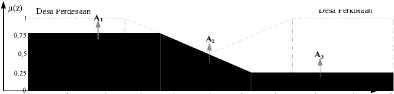
Kemudian hitung luas setiap daerah hasil agregasi desa 1 sebagai berikut:


Daerah Hasil

Agregasi

Desa 1

0,25 x0

0   1   2  3  4   5   6  7

Akses Fasilitas Umum

0

Desa Perkotaan

Desa Perdesaan

0

2

4

16

18

6     a1 8         10        12 a2    14

Status Desa

Gambar 6. Daerah Hasil Agregasi Desa 1


,

71 1 = I 0,75 dz = 0,75zβ ,5 = 5,625; Jo


z 20


^2


f1 2,5 15 —z          1           z2 1 2,5

= ∫7,5 Hddz = ioK ⅛ = 2,5;


Fungsi keanggotaan hasil agregasi desa 1 adalah sebagai berikut:


r20

73 = I 0,25 dz = 0,25z]2 £5 = 1,875.

Jl 2,5                              ,


0,75;0 ≤ z < 7,5

15 —

^sf (z) = )^[Q-;7,5≤z<12,5

0,25;12,5 ≤z≤ 20

Melakukan Defuzzifikasi


Sehingga diperoleh hasil defuzzifikasi sebagai berikut:


z *


21,09375 + 23,958 + 30,46875


75,5205

10


5,625 + 2,5 + 1,875


7,55205 ≈ 7,6


Pertama hitung momen untuk setiap daerah sebagai berikut:

/■7,5

M1 = I (0,75)z dz = 0,375z 2 ]7, 5 Jo

= 21,09375;

, 5 15 — z∖

M2 = J7,5 (—J* ^

Jadi nilai defuzzifikasi untuk desa 1 adalah 7,6.

Hasil Klasifikasi Setiap Desa

Hasil klasifikasi untuk desa 1 sampai desa 59 dapat dilihat pada Tabel 6 berikut.

Tabel 6. Hasil Klasifikasi Setiap Desa

No

Nama Desa

Total Score

z *

μ(z*)

Status Desa

Desa Perdesaan

Desa Perkotaan

Prediksi

Asli

1

Sakti

9

7,6

0,74

0,26

Desa Perdesaan

Desa Perdesaan

2

Bunga Mekar

10

10

0,5

0,5

Desa Perkotaan

Desa Perkotaan

3

Batumadeg

10

10,1

0,49

0,51

Desa Perkotaan

Desa Perkotaan

4

Klumpu

11

12,5

0,25

0,75

Desa Perkotaan

Desa Perkotaan

5

Batukandik

10

10

0,5

0,5

Desa Perkotaan

Desa Perkotaan

6

Sekartaji

10

11,2

0,38

0,62

Desa Perkotaan

Desa Perkotaan

7

Tanglad

11

11,8

0,32

0,68

Desa Perkotaan

Desa Perkotaan

8

Pejukutan

10

10

0,5

0,5

Desa Perkotaan

Desa Perkotaan

59

Besan

8

7,53

0,747

0,253

Desa Perdesaan

Desa Perdesaan


Hasil klasifikasi untuk setiap desa diperoleh dengan mensubstitusikan nilai defuzzifikasinya ke dalam fungsi keanggotaan pada masing-masing himpunan fuzzy variabel output dan menentukan klasifikasi dengan nilai yang diperoleh. Pada Tabel 7 baris pertama yaitu desa 1 (Desa Sakti) dapat dilihat derajat keanggotaan μ(z*) desa perdesaan lebih besar daripada desa perkotaan yaitu 0,74 maka desa 1 terklasifikasi sebagai desa perdesaan. Penentuan status desa untuk desa dua sampai desa 59 juga sama seperti desa 1.

Uji Ketepatan Hasil Klasifikasi

Pengujian dilakukan dengan membandingkan keluaran metode Mamdani dengan data asli. Hasil pengujian disajikan pada Tabel 7.

Tabel 7. Confusion Matrix

Hasil Observasi (actual class)

Hasil Prediksi (predicted class)

Jumlah

Desa Perdesaan

Desa Perkotaan

Desa Perdesaan

4

1

5

Desa Perkotaan

3

51

54

Jumlah

7

52

59

Banyaknya hasil prediksi klasifikasi desa yang sesuai adalah 55 desa, banyaknya prediksi desa dengan status desa perdesaan sedangkan klasifikasi asli yaitu desa perkotaan adalah 3 desa. Banyaknya prediksi desa dengan status desa perkotaan sedangkan klasifikasi asli yaitu desa perdesaan adalah 1 desa dengan jumlah seluruh desa yaitu 59 desa.

Uji ketepatan/ akurasi hasil klasifikasi dapat dihitung dengan rumus berikut :

Tl kuras i =


4 + 51

4 + 1 + 3 + 51


55

59


0,93


= 93%

  • 4. KESIMPULAN DAN SARAN

    A.    KESIMPULAN

Berdasarkan hasil pengolahan data dalam mengklasifikasikan desa perkotaan dan desa perdesaan di Kabupaten Klungkung diperoleh kesimpulan sebagai berikut:

  • 1.    Metode Mamdani dapat digunakan dalam mengklasifikasikan desa di Kabupaten Klungkung. Hasil klasifikasi dengan metode Mamdani menghasilkan 52 desa terklasifikasi menjadi desa perkotaan dan tujuh desa menjadi desa perdesaan dengan tingkat akurasi sebesar 93% antara keluaran metode Mamdani dengan data asli pada 59 desa di Kabupaten Klungkung.

  • 2.    Terdapat perbedaan pada total skor dan status desa antara keluaran metode Mamdani dengan data asli. Dari 59 desa ada empat desa yang terklasifikasi berbeda dengan status desa aslinya yaitu desa: Getakan, Jumpai, Selisihan, dan Pesinggahan.

  • B.    SARAN

Adapun saran yang dapat diberikan pada penelitian tentang klasifikasi desa perkotaan dan desa perdesaan selanjutnya yaitu:

  • 1.    Menggunakan metode model fuzzy yang lain seperti metode Tsukamoto dan metode Sugeno.

  • 2.    Menggunakan variabel tambahan yang lain seperti ketersediaan internet, sehingga diperoleh hasil klasifikasi yang lebih baik.

DAFTAR PUSTAKA

Arifin, S., Muslim, M. A., & Sugiman. (2015). Implementasi Logika Fuzzy Mamdani untuk Mendeteksi Kerentanan Daerah Banjir di Semarang Utara. Scientific Journal of Informatics Vol. 2, No. 2, November 2015, 179-192.

Ayuningtiyas, I. K., Saptono, F., & Hidayat, T. (2007). Sistem Pendukung Keputusan Penanganan Kesehatan Balita Menggunakan Penalaran Fuzzy Mamdani. Seminar Nasional Aplikasi Teknologi Informasi 2007 (SNATI 207), L-65-L71.

Badan Pusat Statistik. (2010). Klasifikasi Perkotaan dan Perdesaan di Indonesia. Jakarta: Badan Pusat Statistik.

Badan Pusat Statistik Kabupaten Klungkung. (2016). Kabupaten Klungkung Dalam Angka. Klungkung: Badan Pusat Statistik Kabupaten Klungkung.

Bojadziev, G., & Bojadziev, M. (2007). Fuzzy Logic for Business, Finance, and Management. Singapore: World Scientific Publishing Co. Pte. Ltd.

Kusumadewi, S.,  & Purnomo, H. (2010).

Aplikasi Logika Fuzzy untuk Pendukung Keputusan. Yogyakarta: Graha Ilmu.

Muthohar, A.,  & Rahayu , Y. (2016).

Implementasi Logika Fuzzy Mamdani pada Penilaian Kinerja Pelayanan Perawat. Journal of Applied Intelligent System, Vol.1, No. 1, 67-76.

210