PERBANDINGAN PROFIT TESTING MODEL DETERMINISTIK DAN STOKASTIK PADA ASURANSI UNIT LINK
on
E-Jurnal Matematika Vol. 7 (2), Mei 2018, pp. 194-202
DOI: https://doi.org/10.24843/MTK.2018.v07.i02.p203
ISSN: 2303-1751
PERBANDINGAN PROFIT TESTING MODEL DETERMINISTIK DAN STOKASTIK PADA ASURANSI UNIT LINK
Valeria Trisna Yunita1§, I Nyoman Widana2§, Luh Putu Ida Harini3
1Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: valey.trisna@gmail.com] 2Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: nwidana@yahoo.com] 3Program Studi Matematika, Fakultas MIPA – Universitas Udayana [Email: ballidah@gmail.com]
§Corresponding Author
ABSTRACT
Profit testing is a method to find out the potential loss or gain of unit link life insurance product. Unit-link life insurance is a combination of life insurance and investment. The aim of this research was to determine the potential benefits or losses of unit-linked life insurance products using a deterministic model and stochastic model. The calculation result using these model for a policy issued to a life aged 35, 45, and 55 and the benefit is paid till age 99 showed that the profit which insurer can claim only for insurance issued to a life age 25 years old.
Keywords: Proftit Testing, Unit-link Life Insurance, Deterministic, Stochastic.
-
1. PENDAHULUAN
Asuransi jiwa (life insurance) merupakan cara sekelompok orang bekerja sama untuk meringankan beban kerugian karena kematian atau hidup matinya seseorang yang dipertanggungkan. Menurut Dickson et al. (2009), asuransi jiwa dibagi menjadi dua yaitu, asuransi tradisional dan asuransi modern. Asuransi jiwa unit link merupakan salah satu dari asuransi jiwa modern. Berbeda dari asuransi tradisional yang hanya menawarkan proteksi saja, asuransi unit link selain menawarkan proteksi juga menawarkan investasi.
Penanggung pada asuransi jiwa, dalam hal ini perusahan asuransi, membayarkan uang pertanggungan (benefit) ketika terjadi klaim. Pada asuransi tradisional besar benefitnya sudah ditentukan pada awal kontrak, sedangkan pada asuransi unit link besar benefitnya sangat bergantung dari hasil investasi. Di Indonesia, produk unit link ini lebih diminati karena dianggap premi yang dibayarkan pada asuransi jiwa tradisional hangus jika selama masa pertanggungan tidak terjadi masalah pada kesehatan dan jiwa (Sartika dan Adinugraha, 2013).
Premi asuransi jiwa unit link yang dibayarkan oleh tertanggung diakomodir oleh perusahaan asuransi. Perusahaan asuransi kemudian membagi premi tersebut ke dalam empat jenis penempatan dana (fund) yang berbeda sesuai dengan keinginan dari pihak tertanggung. Besar benefit yang dibayarkan oleh perusahan asuransi bergantung pada return dari masing-masing penempatan dana, sehingga perusahaan asuransi perlu memperhitungkan produk asuransinya menguntungkan atau merugikan bagi perusahan. Perusahaan asuransi juga mengeluarkan biaya untuk pengadaan polis, pemeriksaan kesehatan, biaya agen, dan lain-lain. Untuk itu, perlu dilakukan profit testing yang merupakan salah satu cara menghitung aliran kas dari perusahaan asuransi pada tiap akhir periode (akhir tahun atau akhir bulan) dari satu kontrak polis asuransi unit link. Adapun tujuan melakukan profit testing adalah mengidentifikasi keuntungan atau kerugian yang didapat dari perusahaan asuransi di setiap akhir periode.
Penelitian terkait mengenai profit testing, Soedibjo dan Fitriati (2009) menggunakan
pendekatan profit testing dalam menghitung penetapan target premi asuransi jiwa syariah untuk mencapai titik impas. Dalam penelitiannya penetapan premi menggunakan pendekatan profit testing bergantung pada produk yang dipasarkan, biaya operasional, kinerja investasi, dan risiko kematian tertanggung. Mandal (2016) juga telah membahas mengenai asuransi unit link di India, contoh ilustrasi perhitungan dalam penelitiannya menghasilkan keuntungan yang menaik setiap tahunnya dengan pendekatan deterministik, sedangkan pendekatan stokastik menghasilkan keuntungan yang naik turun setiap tahunnya. Oleh karena itu, penelitian ini akan membandingkan profit testing model deterministik dan stokastik dari produk asuransi unit link.
-
2. METODE PENELITIAN
Jenis dan Sumber Data
Data yang digunakan dalam penelitan ini adalah data sekunder, yaitu ilustrasi polis yang meliputi umur peserta, premi yang dibayarkan, premi yang dialokasikan, biaya manajemen, biaya perusahaan, manfaat kematian tambahan, data historis dari return, dan Tabel Mortalitas.
Metode Analisis Data
Ada dua pendekatan dalam menganalisis aliran kas, yaitu pendekatan deterministik dan pendekatan stokastik. Pendekatan deterministik menggunakan asumsi return konstan atau sama setiap tahunnya untuk dana yang diinvestasikan oleh pemegang polis, sedangkan pada pendekatan stokastik return untuk dana yang diinvestasikan diasumsikan sebagai variabel acak. Pendekatan deterministik pada profit testing kurang mampu menggambarkan keadaan secara tepat (Dickson et al., 2009)
Akumulasi dari return untuk dana yang diinvestasikan selama setahun selalu bernilai positif diasumsikan mengikuti sebaran distribusi lognormal. Bentuk dari distribusi lognormal tidak simetris sering digunakan dalam menghitung kerugian operasional (Sumendra et al., 2015). Salah satu cara untuk membangkitkan
bilangan acak yang berdistribusi lognormal adalah dengan Simulasi Monte Carlo. Simulasi ini merupakan teknik perhitungan numerik untuk membangkitkan variabel acak dari distribusi tertentu.
Berikut dibahas konsep-konsep yang digunakan dalam perhitungan profit testing pada asuransi jiwa unit link yang meliputi tingkat bunga, fungsi kelangsungan hidup dan profit
testing.
Tingkat bunga yang digunakan dalam investasi merupakan tingkat bunga majemuk. Nilai sekarang dari pembayaran sebesar 1 unit
yang dilakukan t tahun kemudian didefinisikan
sebagai:
vt =
i
(W
(1)
Peluang orang yang berusia + tahun mencapai usia + + t tahun dinotasikan dengan
tpx, sedangkan peluang dari orang yang berusia tahun meninggal dalam jangka waktu tahun dinotasikan dengan yang secara berturut-
turut dapat dihitung dengan,
,Px =⅛l (2)
t‰ =⅛^=1-tp, (3)
Analisis produk dari asuransi dalam waktu tertentu disebut profit testing (Koller, 2010). Profit testing dapat digunakan untuk menghitung potensi keuntungan dari produk asuransi. Profit testing dilakukan dengan menghitung diagram aliran kas setiap periodenya, sehingga dapat diketahui potensi keuntungan atau kerugian yang didapatkan oleh perusahaan asuransi setiap periodenya (Dickson et al., 2009).
Dana pemegang polis ( ) merupakan
jumlah uang dari investasi yang dilakukan oleh pemegang polis pada waktu . Perhitungan dana ini melibatkan Premi yang Dibayarkan ( ),
Premi yang Dialokasikan (TlPt), Bunga Dana Pemegang Polis (it), dan Biaya Manajemen ( ). Perhitungan bunga untuk dana
pemegang polis model deterministik dapat dihitung berdasarkan persamaan,
i t = (A P+ Ft - i)i {,
dengan it merupakan return untuk dana pemegang polis. Sedangkan dana pemegang polis dirumuskan sebagai,
Ft = + Ft-ι +h- MCt
=(1+i{)(APt + Ft-ι)-MCt. (4)
Perhitungan keuntungan yang diperoleh perusahaan melibatkan Premi yang Tidak Dialokasikan (UAPt), Biaya yang dikeluarkan Perusahaan (Ft), Bunga Perusahaan (It), Manfaat Kematian yang Diharapkan (EDBt), dan Biaya Manajemen (MCt). Manfaat Kematian yang Diharapkan merupakan manfaat kematian yang ditanggung perusahaan untuk seorang yang mengikuti kontrak pada tahun ke-t atau dapat dirumuskan sebagai,
EDBt = , (5)
dengan UP merupakan besar manfaat kematian yang ditanggung perusahaan. Keuntungan perusahaan yang diperoleh setiap tahunnya yang kemudian disebut profit vector dirumuskan sebagai,
Prt = + It - Et + MCt - EDBt . (6)
Perkalian profit vector dengan peluang hidup seseorang merupakan keuntungan yang diharapkan pada akhir periode dari 1 kontrak polis, yang dirumuskan dengan
Πt= , untuk t = 1,2,…t (7)
Vektor ∏ disebut profit signature untuk kontrak asuransi unit link t tahun, dengan ∏ =(Πo,Πi,Π2,…,Πt)
=(Pr0 , Pr1 , ιPx Pr2,…,t-ιPχ Prt). (8)
Misalkan r merupakan tingkat bunga, maka nilai sekarang dari profit signature(NPV), dinyatakan sebagai
NPV =∑ "=o Πtvr . (9)
Pada penelitian ini, dana pemegang polis dipengaruhi oleh return. Salah satu asumsi yang digunakan adalah akumulasi dari return berdistribusi lognormal. Salah satu cara untuk membangkitkan akumulasi return yang berdistribusi lognormal adalah dengan menggunakan simulasi Monte Carlo. Misalkan R^, ^2 , ^3 ,…,R^ merupakan barisan dari bilangan acak, dengan R^ merupakan akumulasi pada saat t dari 1 unit yang diinvestasikan pada saat t - 1. Sehingga R^ - 1 merupakan return
dari aset dana pada tahun yang berkaitan. Diasumsikan {ln R^ } merupakan barisan peubah acak yang berdistribusi normal dengan rataan B dan varians σ2 , sehingga {R^} merupakan
barisan peubah acak yang berdistribusi lognormal, sehingga besar dana pemegang polis untuk model stokastik dirumuskan sebagai, Ft=(Ft-ι + APt)(1 + Et-1)-MCt. (10)
Jika Z merupakan bilangan acak dari distribusi N(0,1) maka,
X= (11)
berdistribusi lognormal (B, σ2).
Salah satu kelebihan simulasi Monte Carlo adalah dapat dicari kisaran kerugian dan keuntungannya dari perusahaan asuransi dengan tingkat kepercayaan tertentu (Sari et al., 2017).
Misalkan NPVi merupakan nilai sekarang dari profit signature dari simulasi Monte Carlo ke-i untuk i = 1,2,3…,N , sehingga {NPVi }^1 merupakan sekumpulan dari NPV yang dimodelkan sebagai peubah acak. Selanjutnya misalkan ̅ dan ̅ secara berturut-turut adalah rataan dan simpangan baku dari NPV, maka kisaran kerugian dan keuntungan yang dialami oleh perusahaan asuransi dengan tingkat kepercayaan 95% dapat dinyatakan (Dickson et al., 2009) dalam interval I dengan, _ _
I= ( ̅-1․96 , ̅+1․96 ). (12)
Adapun tahap-tahap analis data dalam penelitian ini sebagai berikut:
-
1. Menghitung nilai Px+k, dan
kPx menggunakan tabel mortalitas untuk usia tertanggung 25,35,45, dan 55 tahun
-
2. Melakukan perhitungan profit testing model deterministik untuk usia tertanggung 25,35,45, dan 55 tahun, dengan langkah-langkah: (a) Menentukan besar premi yang dialokasikan pada saat t (APt); (b)
Menghitung besar bunga dari aset dana pemegang polis pada saat t(U ); (c)
Menentukan besar biaya manajemen pada saat t(MCt); (d) Menghitung dana
pemegang polis pada saat t( Ft) berdasarkan persamaan (4); (e) Menghitung besar premi yang tidak dialokasikan pada saat t(UAPt);
(f) Menghitung biaya yang dikeluarkan perusahaan pada saat t( Et ); (g) Menghitung besar bunga yang diperoleh perusahaan asuransi pada saat t(/j); (h) Menghitung manfaat kematian yang diharapkan pada saat t(EDBt); (i) Menghitung total keuntungan yang diperoleh perusahaan pada saat t(Prt); (j) Menghitung profit signature (Π); (k)
Menghitung Net Present Value (NPV) dari profit signature.
-
3. Melakukan perhitungan profit testing model stokastik untuk usia tertanggung 25,35,45, dan 55 tahun, dengan langkah-langkah: (a) Membangkitkan bilangan acak normal (0,1); (b) Menghitung parameter B (rataan) dan σ (standar deviasi) untuk distribusi lognormal dari data historis return. (c) Menghitung
akumulasi return untuk aset dana pemegang polis (it ) berdasarkan persamaan (11) dengan B dan σ yang diperoleh pada langkah (3.c); (d) Menghitung besar biaya manajemen pada saat t(MCt); (e) Menghitung dana pemegang polis pada saat t( Ft ) berdasarkan persamaan (10); (f) Menghitung total
keuntungan yang diperoleh perusahaan pada saat t( Prt); (g) Menghitung profit signature (∏); (h )Menghitung Net Present Value (NPV) dari profit signature; (i) Menghitung kisaran kerugian dan keuntungan dengan tingkat kepercayaan 95%.
-
4. Membandingkan hasil perhitungan profit testing model deterministik pada langkah (2.k) dengan profit testing model stokastik pada langkah (3.i).
-
3. HASIL DAN PEMBAHASAN
Pada penelitian ini akan dibahas contoh kasus kontrak asuransi unit link pada Perusahaan X untuk usia tertanggung 25,35,45, dan 55 tahun. Besar premi tahunan yang dibayarkan Rp6․000․000,00 dengan masa pembayaran premi selama 15 tahun yang ditanggung hingga usia 99 tahun. Uang pertanggungan untuk usia 25,35,45, dan 55 tahun Rp560․000․000,00; Rp380․000․000,00; Rp280․000․000,00; dan Rp180․000․000,00; sedangkan biaya asuransi bulanan dikenakan secara berturut-turut
Rp100․800,00; Rp72․200,00; Rp92․167,00; dan Rp120․600,00. Besar biaya administrasi setiap bulannya Rp27․500,00 dan biaya pengelolaan setiap tahunnya 2% yang dibayarkan selama berlakunya asuransi. Premi tahunan yang dibayarkan dibagi menjadi 2 yaitu Premi Berkala dan Premi Top Up, dengan pembagian Premi Berkala sebesar Rp4․000․000,00 dan Premi Top Up sebesar Rp2․000․000,00. Besar alokasi premi setiap tahunnya disajikan dalam Tabel 1.
Pada Tabel 1, Premi Berkala belum membentuk investasi pada tahun ke-1, sehingga pemotongan untuk biaya pengelolaan, biaya asuransi, dan biaya administrasi untuk tahun pertama dilakukan pada tahun ke-3. Biaya akuisisi dari ilustrasi kontrak dibebankan pada premi berkala yang tidak diinvestasikan. Dalam penelitian ini diasumsikan tidak adanya penarikan investasi dan penambahan premi. Jika investasi yang terbentuk tidak cukup untuk membayar biaya administrasi dan biaya asuransi maka kontrak polis dianggap batal.
Tabel 1. Porsi Investasi
|
Porsi Investasi (tahun ke-) | ||||
|
1 |
2 |
3, 4, dan 5 |
6 dst | |
|
Premi Berkala |
0% |
40% |
85% |
100% |
|
Premi Top Up |
95% |
95% |
95% |
95% |
Sumber: Ilustrasi Polis
Nilai peluang kPx dapat dihitung menggunakan persamaan (2), dengan hubungan,
tPx = ․ k-lPx
Selanjutnya besar premi yang dibayarkan oleh tertanggung setiap tahunnya (Pt ) Rp 6․000․000,00 selama 15 tahun.Berdasarkan Tabel 1. diperoleh, AP1 = Rp1․900․000,00;
AP2 = Rp3․500․000,00;
, , = Rp5․300․000,00;
APt = Rp5․900․000,00; untuk t=6,7,8, …,15, dan APt = Rp0,00 untuk t lainnya, dengan t menyatakan tahun dari kontrak asuransi unit link yang ditanggung hingga usia
99 tahun. Sehingga batasan t untuk usia tertanggung 25,35,45, dan 55 tahun secara berturut-turut 74, 64, 54, dan 44.
Biaya manajemen dalam contoh kasus ini meliputi biaya asuransi, biaya pengelolaan, dan biaya administrasi. Dalam contoh kasus penelitian ini, biaya manajemen dievaluasi setiap tahunnya, biaya asuransi dan biaya administrasi terlebih dahulu dikonversikan menjadi biaya tahunan. Tingkat bunga perusahaan tahunan yang digunakan dalam penelitian ini 6,5%, sehingga tingkat bunga bulanan yang digunakan,
(1+X) 12 = 1 + 0,065, dengan X menyatakan bunga bulanan
X = 0,005262 = 0,5262%
Pembayaran bulanan Rp1,00 diakhir bulan dikonversikan menjadi tahunan dengan faktor tingkat bunga bulanan 0,5262% menjadi
P12 = (1 + 0,005262) 11 + (1 + 0,005262)10
+ (1 + 0,005262)9 + ⋯+
(1 + 0,005262)0
= 12,41846
Besar biaya manajemen setiap tahunnya dengan return konstan 5% untuk usia tertanggung 25,35,45, dan 55 tahun secara berturut-turut dapat dihitung,
MCt = Rp1․593․289,00 + (APt + Pt-ι)(1+
MCt = Rp1․238․121,00 + (Apt + Ft-i)(1+
MCt = Rp1․486․080,00 + (APt + Pt-i)(1+
MCt = Rp1․839․174,00 + (APt + Pt-i)(1+
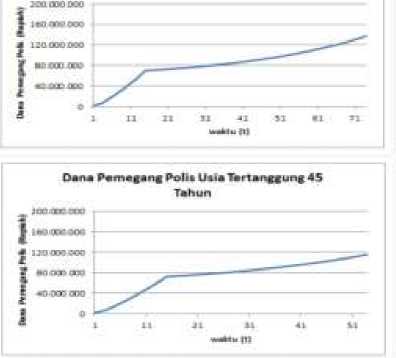
Berdasarkan persamaan (4) dana pemegang polis pada saat ke-t dapat disajikan pada Gambar 1. Gambar 1 memperlihatkan bahwa dana pemegang polis mengalami kenaikan setiap tahunnya, namun pada t = 16 dan seterusnya laju kenaikannya menurun dikarenakan pembayaran premi hingga t = 15.
Dane Pemegsnf Polii Usla Tertanuunf 25 Tahun
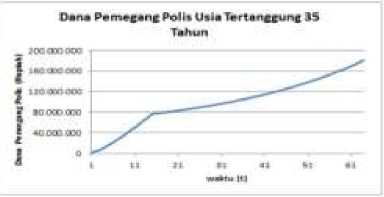
Dana Petnecarif Polls Usia Tertanuung 55 TohUH
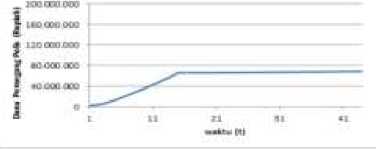
Gambar 1. Dana Pemegang Polis Usia Model Deterministik
Premi yang Tidak Dialokasikan merupakan selisih antara Premi yang Dibayarkan dan Premi yang Dialokasikan sehingga diperoleh, UAP1 = Rp4․100․000,00;
UAP2 = Rp2․500․000,00;
, , = Rp700․000,00;
UAPt = Rp100․000,00 untuk t=6,7,8,…,15, dan UAPt = Rp0,00 untuk t lainnya.
Biaya yang dikeluarkan dalam ilustrasi polis Perusahaan X merupakan besar premi berkala yang tidak dialokasikan untuk investasi, dari Tabel 1. diperoleh, Po = Rp4․000․000,00;
Ei = Rp0,00;
E2 = Rp2․400․000,00;
, , = Rp600․000,00 dan
Et = Rp0,00 untuk t lainnya.
Bunga yang diperoleh perusahaan menggunakan suku bunga bebas risiko 6,5% yang merupakan Suku Bunga Bank Indonesia. Selanjutnya, dihitung manfaat kematian yang diharapkan menggunakan persamaan (5). Hasil yang diperoleh pada langkah sebelumnya digunakan untuk menghitung profit vector menggunakan persamaan (6). Pada Gambar 2. yang menyajikan hasil profit vector, dapat dilihat
bahwa keuntungan tahunan yang diperoleh perusahaan menurun seiring dengan bertambahnya waktu. Hal tersebut disebabkan oleh manfaat kematian yang diharapkan, yang ditanggung oleh perusahaan semakin besar setiap tahunnya. Profit vector yang diperoleh kemudian dikalikan dengan peluang hidup k tahun ( kpx) sehingga diperoleh profit signature.
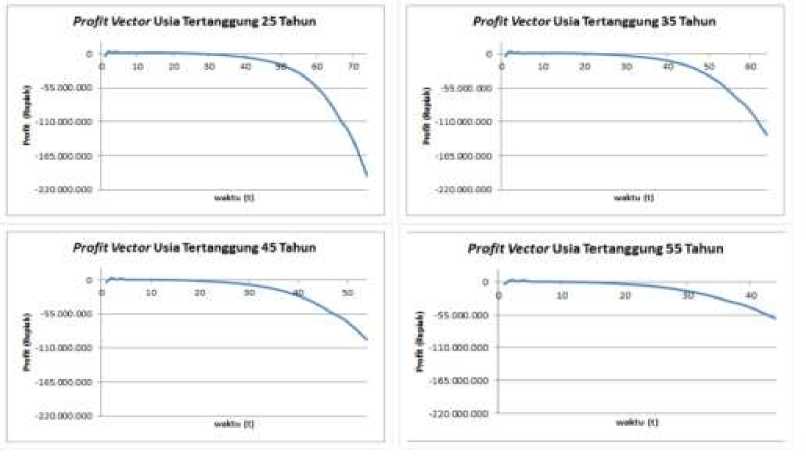
Gambar 2. Profit Vector Model Deterministik
Keuntungan total yang diperoleh perusahaan dihitung menggunakan persamaan (9), dengan tingkat bunga yang digunakan 6,5%. Nilai sekarang dari profit signature (NPV) untuk usia tertanggung 25, 35, 45, dan 55 tahun disajikan pada Tabel 2.
Tabel 2. Net Present Value Model Deterministik
|
Usia |
NPV (Rupiah) |
|
25 |
3.316.182 |
|
35 |
-7.258.475 |
|
45 |
-16.643.320 |
|
55 |
-18.729.422 |
Berdasarkan Tabel 2 nilai Net Present Value -Rp 7․258․475,00 berarti perusahaan mengalami kerugian sebesar Rp 7․258․475,00 untuk 1 orang yang mengikuti kontrak asuransi. Semakin besar usia tertanggung keuntungan yang diperoleh perusahaan semakin menurun.
Selanjutnya akan dihitung profit testing menggunakan model stokastik, khususnya
dengan mengasumsikan returnnya mempunyai distribusi lognormal.
Sebelum membangkitkan bilangan acak yang berdistribusi lognormal diperlukan parameter P (rataan) dan σ (standar deviasi). Parameter ini dihitung berdasarkan data Tabel 3. yang diperoleh dari ilustrasi kontrak polis.
Tabel 3. Data Historis Tingkat
|
Tahun |
Return (Rt ) |
Akumulasi Return (1+Rt) |
ln(1 + Rt) |
|
2012 |
0,1039 |
1,1039 |
0,098849364 |
|
2013 |
-0,0254 |
0,9746 |
-0,025728149 |
|
2014 |
0,2697 |
1,2697 |
0,238780652 |
|
2015 |
-0,194 |
0,806 |
-0,215671536 |
|
2016 |
0,081 |
1,081 |
0,077886539 |
Pada penelitian ini diasumsikan akumulasi return berdistribusi lognormal. Nilai Kolom ke-4 pada Tabel 3 digunakan untuk menaksir/menduga nilai parameter P dan σ dengan menggunakan persamaan,
∑t=ιln(1+Rt
= dan
n
σ ∑ ⅛1(ι∏(1+Rt) -n) 2
\ n-1
Nilai parameter yang diperoleh adalah
μ = 0,0348 dan σ = 0,1688. Akumulasi return untuk aset dana pemegang polis dapat ditentukan dengan menggunakan persamaan (11), dengan nilai-nilai parameter yaitu = 0,0348 dan σ = 0,1688, sehingga persamaan (11) dapat ditulis sebagai:
R= ,0348 +0,1688z
dengan Z merupakan bilangan acak berdistribusi N(0,1).
Biaya manajemen untuk model deterministik dapat dihitung menggunakan persamaan,
MCt = Rp1․593․289,00 + (APt + Ft-ι)
(Rt)2% untuk t=1,2,3,…,74. (17)
MCt = Rp1․238․121,00 + (Apt + Ft-ι)
(Rt)2% untuk t=1,2,3,…,64. (18)
MCt = Rp1․486․080,00 + (APt + Ft-ι)
(Rt)2% untuk t=1,2,3,…,54. (19)
MCt = Rp1․839․174,00 + (APt + Ft-ι)
(Rt)2% untuk t=1,2,3,…,44. (20)
Dana pemegang polis model stokastik dapat dihitung menggunakan persamaan (10) dengan nilai-nilai yang diperoleh pada langkah sebelumnya. Hasil perhitungan dana pemegang polis model stokastik dari satu simulasi disajikan pada Gambar 3. Gambar 3 memperlihatkan dana pemegang polis model stokastik mengalami fluktuasi.

Gambar 3. Dana Pemegang Polis Model Stokastik
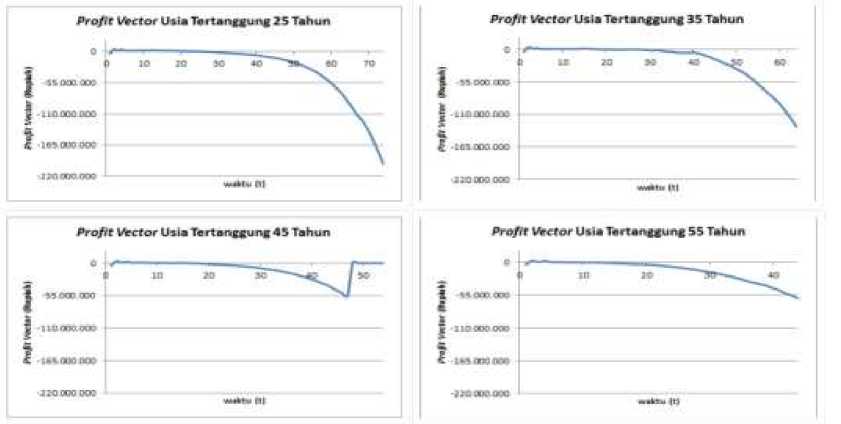
Gambar 4. Profit Vector Model Stokastik
Profit Vector untuk model stokastik dihitung menggunakan persamaan (6). Pada Gambar 4. yang menyajikan hasil profit vector model stokastik dari satu simulasi, dapat dilihat profit vector dari tahun ke tahun mengalami penurunan. Hal ini disebabkan dengan manfaat kematian yang ditanggung perusahaan dari tahun ke tahun semakin tinggi
Nilai sekarang dari profit signature untuk model stokastik (NPV) dari satu simulasi dengan menggunakan persamaan (9) disajikan pada Tabel 3.
Tabel 3. NPV Model Stokastik
|
Usia |
NPV (Rupiah) |
|
25 |
-270.370 |
|
35 |
-3.265.959 |
|
45 |
-17.331.734 |
|
55 |
-19.537.338 |
Berdasarkan Tabel 3 dapat dilihat Net Present Value untuk usia tertanggung 25 tahun -Rp270․370,00 dan seterusnya. Net Present Value bernilai -Rp270․370,00 memiliki arti perusahaan mengalami kerugian sebesar Rp270․370,00 dari 1 orang yang mengikuti kontrak asuransi.
Kisaran kerugian dan keuntungan dengan tingkat kepercayaan 95% dapat dihitung menggunakan persamaan (12). Dengan bantuan software Microsoft Excel diperoleh rataan dan
simpangan baku dari 10.000 simulasi dengan kisaran kerugian dan keuntungan disajikan pada Tabel 4. Tabel 4 memperlihatkan bahwa kerugian maksimum yang dialami perusahaan untuk usia tertanggung 35 tahun adalah Rp5․333․317,00, sedangkan kerugian minimum yang dialami perusahaan adalah
Rp5․057․219,00, dan demikian seterusnya. Selain itu kisaran kerugian dan keuntungan yang dialami perusahaan asuransi semakin kecil seiring dengan bertambahnya usia.
Perbandingan hasil Net Present Value model determinisik dan stokastik dapat dilihat pada Tabel 5. Tabel 5 memperlihatkan bahwa nilai Net Present Value dengan menggunakan model deterministik memberikan hasil yang jauh berbeda dengan model stokastik. Selain itu keuntungan total yang diperoleh perusahaan menggunakan model deterministik dan stokastik menurun seiring dengan bertambahnya usia tertanggung. Perbedaan hasil Net Present Value model deterministik dan stokastik dipengaruhi salah satunya oleh dana pemegang polis.
Hasil perhitungan yang berbeda jauh tersebut disebabkan return tetap yaitu 5% pada model determistik, sedangkan pada model stokastik akumulasi return yang diasumsikan berdistribusi lognormal dengan rataan 0,0348 dan standar deviasi 0,1688.
Tabel 4. Kisaran Kerugian dan Keuntungan
|
Usia (tahun) |
Rataan ( ̅) (Rupiah) |
Standar Deviasi ( ̅) (Rupiah) |
Kisaran Kerugian dan Keuntungan (Rupiah) |
|
25 |
8.723.733 |
7.169.638 |
(8․583․208, 8․864․258) |
|
35 |
-5.195.268 |
7.043.313 |
(-5․333․317, -5․057․219) |
|
45 |
-15.043.426 |
5.173.737 |
(-15․144․831, -14․942․020) |
|
55 |
-17.721.972 |
3.027.507 |
(-17․781․311, -17․662․632) |
Tabel 5. Perbandingan NPV Model Deterministik dan Stokastik
|
Usia |
Model Deterministik (Rupiah) |
Model Stokastik (Rupiah) |
|
25 |
3.316.182 |
8.723.733 |
|
35 |
-7.258.475 |
-5.195.268 |
|
45 |
-16.643.320 |
-15.043.426 |
|
55 |
-18.729.422,00 |
-17.721.972 |
Nilai negatif dari Net Present Value berarti perusahaan mengalami kerugian untuk usia
tertanggung 35,45, dan 55 tahun dalam hal ini polis berlaku sampai dengan usia tertanggung mencapai 99 tahun. Nilai negatif ini dapat dikarenakan harga premi yang terlalu murah atau uang pertanggungan terlalu besar. Sehingga dana yang terkumpul tidak cukup (perusahan mengalami kerugian). Tetapi, jika polisnya dijamin berlaku dalam 10 tahun saja, seperti dalam ilustrasi kontrak, maka perusahan tidak
akan mengalami kerugian yang tercantum pada Tabel 6 berikut.
Tabel 6. NPV untuk Kontrak 10 Tahun
|
Usia (tahun) |
Model Deterministik (Rupiah) |
Model Stokastik (Rupiah) |
|
25 |
11.422.275 |
11.434.124 |
|
35 |
6.903.947 |
7.267.713 |
|
45 |
4.261.191 |
4.223.238 |
|
55 |
1.497.675 |
1.694.452 |
Hasil perhitungan profit testing untuk kontrak yang ditanggung hingga usia 99 tahun pada model stokastik menghasilkan keuntungan untuk usia tertanggung 25 tahun. Sedangkan untuk usia tertanggung 35, 45, dan 55 tahun mengalami kerugian. Keuntungan dapat terjadi jika kontrak berlaku 10 tahun. Hasil perhitungan profit testing model deterministik dan model stokastik menghasilkan Net Present Value yang jauh berbeda. Hal ini disebabkan oleh return konstan 5% pada model deterministik dan akumulasi return yang berdistirbusi lognormal untuk model stokastik.
Hasil perhitungan dengan model stokastik dapat dicari kisaran kerugian dan keuntungan yang diperoleh dengan simulasi Monte Carlo menggunakan tingkat kepercayaan 95%.
DAFTAR PUSTAKA
Dickson, D.C.M., Hardy, M.R. & Waters, H.R., 2009. Actuarial Mathematics for Life Contingent Risk. Cambridge: University Press.
Koller, Michael. 2010. Stochastic Models in Life Insurance. New York: Springer.
Mandal, Satrajit. 2016. Unit linked Insurance Plans and Their Applications in India. Thesis. University of Tartu.
Sari, D. K., Widana, I N., dan Sari, K. 2017. Perbandingan Hasil Perhitungan Premi Asuransi Jiwa Endowment Suku Bunga Vasicek dengan dan Tanpa Simulasi Monte Carlo. E-Jurnal Matematika Vol. 6, No.1,74-82.
Sartika, M., Adinugraha, H.H. 2013. Konsep dan Implementasi Pengelolaan Dana Premi Unit Link Syari’ah. Jurnal Asuransi dan
Manajemen Risiko Vol. 1, No. 1.
Soedibjo, S. Fitriati, R. 2009. Penetapan Target Premi Asuransi Jiwa Syariah untuk Mencapai Titik Impas dengan Pendekatan Model Profit testing. Bisnis & Birokrasi, Jurnal Ilmu Administrasi dan Organisasi Vol.16, No.2, 56-67.
Sumendra, G., Dharmawan, K., Widana, I N. 2015. Menentukan Harga Kontrak Berjangka Nilai Tukar Rupiah Terhadap Dollar As Menggunakan Distribusi Lognormal. E-Jurnal Matematika Vol. 4, No.2, 43-48.
202
Discussion and feedback