MEMBANDINGKAN RISIKO SISTEMATIS MENGGUNAKAN CAPM-GARCH DAN CAPM-EGARCH
on
E-Jurnal Matematika Vol. 6 (4), November 2017, pp. 241-247
DOI: https://doi.org/10.24843/MTK.2017.v06.i04.p172
ISSN: 2303-1751
MEMBANDINGKAN RISIKO SISTEMATIS MENGGUNAKAN CAPM-GARCH DAN CAPM-EGARCH
Viky Ameliah1§, Komang Dharmawan2, I Nyoman Widana3
1Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: vicky.amelia1612@gmail.com] 2Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email:dharmawan.komang@gmail.com] 3Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: nwidana@yahoo.com]
§Corresponding Author
ABSTARCT
In making stock investments, investors usually pay attention to the rate of return and risk of the stock investment. To calculate risk using capital asset pricing model (CAPM), GARCH, and EGARCH. The data used in this study is secondary data in the form of daily closing price (daily close price), JII price index and monthly SBI rate. All data were processed using matlab 13. The research sample consisted of 6 flagship shares for the period of 2013-2017 ie ADHI, SMGR, UNTR, BSDE, ICBP, KLBF. The conclusion of the research is the beta of each stock including aggressive beta because beta greater than 1. For return CAPM GARACH and CAPM EGARCH obtained Kalbe Farma stock (KLBF) has small beta and big return means GARCH and EGARCH model equally Can predict that stock KLBF shares the least risk and large returns among the six stocks.
Keywords: risk, return, beta, CAPM, GARCH, EAGRCH, shares of JII.
Kehadiran pasar modal akan memperbanyak pilihan investasi, sehingga kesempatan untuk memilih investasi yang sesuai dengan preferensi investor akan semakin besar. Salah satu bentuk investasi finansial yang ada di pasar modal Indonesia yaitu saham syariah, dimana indeks saham ini tercermin dalam Jakarta Islamic Index (JII). Kegiatan investasi memiliki tujuan yaitu untuk mendapatkan sejumlah keuntungan atau laba dalam jumlah tertentu. Dalam melaksanakan kegiatan investasi, seorang investor selalu diharapkan pada dua hal yaitu tingkat keuntungan / pengembalian (return) dan risiko yang mungkin timbul akibat adanya ketidakpastian (uncertainty).
Tujuan dari investasi sendiri adalah memperoleh return yang optimal, artinya membeli aset yang memberikan pendapatan paling tinggi dengan risiko tertentu. Pada dasarnya pendapatan berbanding lurus dengan risiko yang dihadapi, artinya jika perusahaan menginginkan pendapatan yang tinggi maka
perusahaan tersebut akan menghadapi risiko yang besar pula. Jadi dalam berinvestasi pada pasar modal, diperlukan pertimbangan dan analisis yang mendalam untuk menjamin keuntungan yang diperoleh pemodal.Salah satu analisis yang dapat diukur adalah menghitung risiko.
Ada dua risiko yang akan ditanggung oleh pemodal, yaitu risiko sistematis dan risiko tidak sistematis. Menurut Husnan (2005) risiko sistematis adalah risiko yang tidak bisa dihilangkan dengan diversifikasi saham, sedangkan risiko tidak sistematis adalah risiko yang bisa dihilangkan dengan diversifikasi saham. Karena pemodal umumnya tidak menginvestasikan semua dananya pada suatu saham, pemodal melakukan diversifikasi saham, sehingga risiko yang hilang karena diversifikasi tersebut tidak relevan dalam perhitungan risiko. Hanya risiko yang tidak bisa hilang dengan diversifikasilah yang relevan dalam perhitungan risiko.
Pada penelitian sebelumnya Penerapan Risiko Sistematis Saham Menggunakan CAPM-GARCH terdapat kelemahan yaitu Model GARCH tidak mampu mengatasi permasalahan pengembalian harga saham memiliki kolerasi negatif dengan perubahan dalam volatilitas pengembaliannya (pengaruh asimetrik). Untuk menangkap asimetri negatif yang dinamis yang biasanya ada pada data keuangan digunakan model EGARCH. Cara menghitung risiko sistematis saham menggunakan Model EGARCH dimana model tersebut mampu menangkap asimetris negatif yang dinamis yang biasanya ada pada data keuangan, yang disebut efek pengaruh (leverage effect). Untuk menghitung risiko pada saham, digunakan Capital Asset Pricing Model (CAPM) dan Model Exponential Generalized Autoregressive Conditional (EGARCH). Pada CAPM yang diukur adalah risiko sistematis, yang disebut β (beta). Sedangkan pada EGARCH yang diukur adalah peramalan volatilitas dan return saham. Volatilitas merupakan simpangan baku bersyarat dari suatu data keuangan yang bertujuan untuk mengukur naik turunnya return suatu investasi. Selanjutnya nilai dari model CAPM-GARCH yang diperoleh dibandingkan dengan model CAPM-EGARCH.
Data yang digunakan adalah data sekunder berupa harga penutupan saham harian (daily closing price). Saham-saham tersebut tergabung dalam indeks harga Jakarta Islamic Index.
Jenis penelitian yang dilakukan yaitu studi kasus terhadap nilai beta (risiko sistematis) yang datanya berasal dari data historis saham-saham yang ada di Jakarta Islamic Index. Studi kasus yang dilakukan dengan melakuakan simulasi untuk penentuan nilai komoditas pada waktu T. Data yang digunakan yaitu data sekunder berupa data harian. Data diambil pada situs www.duniainvestasi.com.
Langkah-langkah yang digunakan untuk menentukan nilai beta meggunakan metode CAPM-GARCH dan CAPM EGARCH adalah:
-
1. Mencari dan menentukan data historis masing-masing saham.
-
2. Eksplorasi data dengan melihat pergerakan harga saham melalui plot deret waktu harga saham untuk melihat pergerakan saham.
-
3. Data saham dikonveksikan dalam bentuk return, kemudian data return diplot untuk melihat kestasioneran data tersebut.
R-=-(⅛τ) (1)
-
4. Menguji ada atau tidaknya efek GARCH dan koefisien korelasi menggunakan Ljung-Box.
Q = n(n + 2)∑ ^ ^ (2)
-
5. Mengestimasi nilai volatilitas (standart deviasi) dan return.
-
6. Menghitung beta dengan CAPM setelah mendapat hasil ramalan volatilitas dan return menggunakan EGARCH..
R. _ Cov(RbRM)
Pl VAR(Rm) ’
-
7. Menghitung tingkat pengembalian saham menggunakan CAPM.
E (Rj) = Rf+ (E(Rm)-R^j (4)
-
8. Membandingkan Expecetd Return CAPM-GARCH dan CAPM-EGARCH.
Definisi Indeks JII (Jakarta Islamic Index)
Jakarta Islamic Index (JII) merupakan indeks yang diharapkan menjadi tolak ukur kinerja saham – saham yang berbasis syariah serta untuk mengembangkan pasar modal syariah. Jakarta Islamic Index terdiri dari 30 saham yang dipilih dari saham – saham yang sesuai dengan Syariah Islam.
Tabel 1. Beberapa Perusahaan Yang Tercantum di JII
|
Nama Perusahaan |
Saham |
|
Adhi Karya (Persero) Tbk |
ADHI |
|
Bumi Serpong Damai Tbk |
BSDE |
|
Kalbe Farma Tbk |
KLBF |
|
Semen Indonesia (Persero) Tbk |
SMGR |
|
Indofood CBP Sukses Makmur Tbk |
ICBP |
|
United Tractors Tbk |
UNTR |
Keenam saham di atas termasuk dalam saham-saham unggulan di JII, karena harga sahamnya mahal.
Analisis Kasus
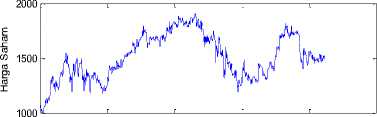
Secara acak diambil salah satu saham yaitu saham KLBF. Banyaknya data saham KLBF yang terkumpul dari periode 2/1/2013 sampai dengan 27/3/2017 adalah sebanyak 1094 data. Adapun grafik pergerakan dari data saham perusahaan tersebut pada gambar 1
Harga penutupan harian Saham KLBF
2013 2014 2015 2016 2017 2018
Tanggal Penjualan
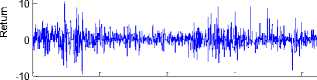
Tingkat Pengembalian (Return) KLBF 20
2013 2014 2015 2016 2017 2018
Tanggal Penjualan
Gambar 1. Plot Data Saham KLBF (atas) dan Return Saham KLBF (bawah) Periode 2/1/2017 sampai 27/3/2017
Berdasarkan Gambar 1 dapat diketahui bahwa pola data cendrung tidak stasioner. Untuk mengetahui tingkat kestasioneran saham tersebut, maka data diubah ke dalam bentuk return. Dapat dilihat return dengan pola data saham KLBF yaitu menyebar pada titik nol.
Model GARCH dan EGARCH
Sebelum dilakukan pemodelan GARCH dan EGARCH, akan dilakukan uji Ljung-Box dan Engle ARCH. Uji Ljung-Box digunakan untuk uji autokorelasi return dan residual, jika H1 berarti menolak H0, artinya data berotokorelasi. Tujuan dari uji ini adalah untuk melihat apakah return dari tingkat pengembalin masing-masing saham berotokorelasi atau tidak. Dari hasil uji saham KLBF tingkat pengembalian (return) menunjukkan adanya sifat autokorelasi cukup signifikan dimana penerimaan hipotesis H1 dengan p=0,0176 untuk taraf signifikan 0,05,
jadi pemodelan return dengan AR (1) adalah valid. Selain dengan uji Ljung-Box, secara virtual juga terlihat pada gambar berikut:
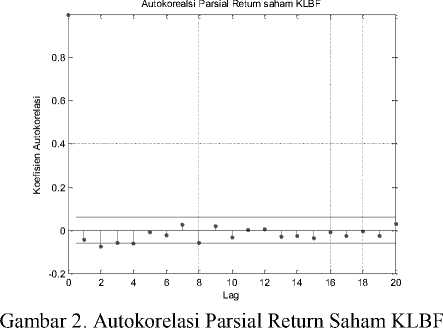
Hasil yang sama juga di tunjukkan oleh data saham lainnya. Lihat pada tabel berikut:
Tabel 2. Hasil Uji Ljung-Box Masing-masing Saham
|
Nama Saham |
α |
Prob* |
|
ADHI |
0,05 |
0,2378 |
|
BSDE |
0,05 |
0,0556 |
|
KLBF |
0,05 |
0,0176 |
|
SMGR |
0,05 |
0,0004 |
|
ICBP |
0,05 |
0,6701 |
|
UNTR |
0,05 |
0,025 |
Terlihat pada tabel 2 bahwa da tiga saham yang return atau tingkat pengembalian sham tidak berautokorelasi, yaitu saham ADHI, BSDE dan ICBP.
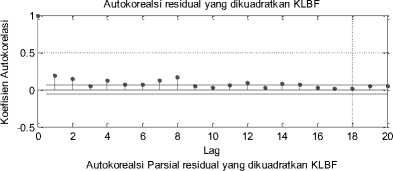
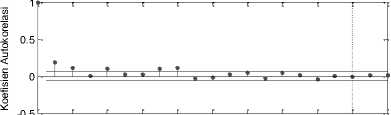
0 2 4 6 8 10 12 14 16 18 20
.
Lag
Gambar 3. Autokorelasi Residual yang dikuadratkan dan Autokorelasi Parsial Residual yang dikuadratkan
Terlihat dari gambar 3 adanya sifat autokorelasi cukup jelas. Dengan adanya titik-titik yang melewati dua garis horizontal yang sejajar pada lag-lag tertentu. Untuk uji Engle’s ARCH untuk mengetahui ada tidaknya sifat heteroskedastik, yaitu sifat ketakstasioner data dalam varians untuk lag 2. Hasil uji ini menunjukkan penerimaan hipotesis H1 dengan p=[0,000012]. Dengan ditolaknya hipotesis nol, maka hasil ini menyarankan model GARCH cukup sesuai untuk memodelkan varians data return saham KLBF. Setelah diketahui adanya efek GARCH pada saham KLBF, tahap selanjutnya memilih model yang terbaik. Pada dasarnya ketika melakukan uji dengan Engle’s ARCH untuk lag 2, pada saat yang sama kita menguji kelayakan model GARCH (1,1) karena model ARCH dengan inovasi lag 2 adalah ekivalen dengan model GARCH(1,1) (Huang, et al., 2010).
Tabel 3. Model GARCH (1,1) pada Masing-masing Saham Perusahaan
|
Saham |
Model GARCH(1,1) |
|
SMGR |
rt = + et ∖ = -0,0333702 + et ∖ σt = + «16t-l + ω1σ,L1 = 0,263616 + 0,0778865et-ι + 0,865604σt-ι I |
|
ICBP |
- |
|
UNTR |
rt = + et ∖ = 0,0620042 + et ∖ σt2 = + «i62-i + ωiσt2.1 = 0,370165 + 0,0793694et-ι + 0,856492σt-ι ∖ |
|
ADHI |
rt = + et ∖ = 0,067258 + et ∖ σ? = + «16t-l + ωiσt2.1 ∖ = 0,151143 + 0,398959et-ι + 0,941925σt-ι I |
|
BSDE |
rt = + et ∖ = 0,0882699 + et ∖ σt2 = + «l^i + Wifft2-I = 0,430541 + 0,0958271et-l + 0,836192σt-ι |
|
KLBF |
rt = + et = 0,0799755 + et ∖ σt = + «16t-l + ωiσt2-1 = 0,11662 + 0,0617688et-ι + 0,90963σt-ι |
Dapat dilihat bahwa saham ICBP tidak terdapat model GARCH karena setelah dilakukan uji Engle ARCH tidak terdapat efek GARCH.
Tabel 4. Model EGARCH(1,1) Masing-masing Saham Perusahaan
|
Saham |
EGARCH(1,1) | ||
|
SMGR |
yt = + Et = -0,107894 + Et P Q logσ} = +∑Yt log⅛Li +∑aJ' |
εt-j σ<-J | |
|
Q γ π +∑ f' [e ] = 0,909098 + 0,948001 logσ^i + 0,143348 σ - 0,0906677 |
-J -J [ ] Vt-i | ||
|
ICBP |
Yt = + Et = -0,32168 + εt p Q logσ} = +∑Yi log⅛Li +∑aJ' i=ι j=ι |
εt-j σ<-J | |
|
+∑ f' [ ] εt- = 1,84005 + 0,10602logσ^i+1 + 0,608867[ ] |
-j -j | ||
|
UNTR |
Yt = + Et = 0,0901565 + Et P Q logσ} = +∑Yi log⅛Li +∑aJ' |
εt-j σ<-J | |
|
Q γ π +∑ f' [e ] = 0,118075 + 0,936054log∣ + 0,150594 σ - 0,0129736 |
tf-i -J -J [ ] Vt-i | ||
|
ADHI |
Yt = + Et = 0,00825372 + εt p Q logσ^ = +∑Yi ^ogσ^i +∑aJ' i=ι j=ι |
εt-J σt-J | |
|
+∑ [S ] = 0,0316284 + 0,988418logσ^ + 0,0828706 - 0,0300885 |
i εJ~L [ ^zl ] Vt-i | ||
|
BSDE |
yt = + εt = 0,0239647 + εt p Q Iogaf = +∑Yi logσ^i +∑aJ' |
εt-j σt-∣ | |
|
i-1 j-1 Q γ +∑ f' [S ] = 0,247533 + 0,869536logoff + 0,263242 σ - 0,0861572 |
-j [ ] | ||
|
KLBF |
Yt = + εt = 0,0371914 + εt p Q Ioga^ = +∑Yi iog⅛Li +∑aJ' |
εt-j σt-∣ | |
|
q Γ 1 +∑ fi [S ] = 0,487283 + 0,969695logoff + 0,116228 σ - 0,0726593 |
-j [⅛ ] | ||
Perhitungan Beta
Setelah mendapatkan model GARCH dan EGARCH masing-masing saham, langkah selanjutnya menghitung beta menggunkan motode CAPM. Perhitungan beta pada masing-masing saham dilakukan dengan menggunkan program Matlab R2013 dengan hasil sebagai berikut:
Tabel 5. Hasil Perhitungan Beta Pada Masing-Masing Saham Perusahaan
|
Saham |
Beta GARCH |
Beta EGARCH |
|
SMGR |
1,5095 |
1,7192 |
|
ICBP |
-0,0519 |
2,5729 |
|
UNTR |
1,6840 |
1,7529 |
|
ADHI |
1,7612 |
2,1284 |
|
BSDE |
1,7841 |
1,8970 |
|
KLBF |
1,3660 |
1,5744 |
Berdasarkan hasil perhitungan beta, saham-saham di atas dapat dikatakan saham agresif. Saham-saham yang agresif adalah saham-saham yang nilai betanya lebih besar daripada rata-rata beta pasar (lebih besar daripada 1). Saham-saham diatas termasuk saham-saham unggulan di Jakarta Index Islam. Artinya saham-saham di atas memiliki risiko yang besar dan juga return yg besar. Saham-saham diatas satu, mengindikasikan bahwa saham tersebut sangat agresif terhadap pasar, sehingga apabila pasar secara keseluruhan naik satu poin, maka saham-saham tersebut naik menjadi lebih besar dari satu poin. Begitu pula sebaliknya.
Capital Asset Pricing odel (CAPM)
E( Rj)=Rf+(E(rm)-Rf ) βj (2.8) Hasil yang diharapkan pada aset tertentu sama dengan tingkat bebas risiko ditambah premi yang bergantung pada aset beta dan perkiraan premi risiko pada portofolio pasar.
Tabel 6. Return Masing-Masing Saham Menggunkan Beta CAPM GARCH
|
Nama Saham(j) |
Rf |
Beta (βj∖ |
(^m - Rr ) βl ∖ |
Ri = +( ^m - Rf ) βl | |
|
SMGR |
0,0550 |
0,0357 |
1,5095 |
-0,0291 |
0,02581 |
|
ICBP |
0,0550 |
0,0357 |
-0,0519 |
-0,0010 |
0,05604 |
|
UNTR |
0,0550 |
0,0357 |
1,6840 |
-0,0325 |
0,02254 |
|
ADHI |
0,0550 |
0,0357 |
1,7612 |
-0,0339 |
0,02101 |
|
BSDE |
0,0550 |
0,0357 |
1,7841 |
-0,0344 |
0,02057 |
|
KLBF |
0,0550 |
0,0357 |
1,3660 |
-0,0263 |
0,02866 |
Tabel 7. Return Masing-Masing Saham Menggunakan Beta CAPM EGARCH
|
Nama Saham(j) |
Rf |
Rm |
Beta ( βj ) |
(R-M - Rf ) β' ∖ |
Ri = +( ^m - Rf ) β< ∖ |
|
SMGR |
0,0550 |
0,0357 |
1,7192 |
-0,0332 |
0,02182 |
|
ICBP |
0,0550 |
0,0357 |
2,5729 |
-0,0496 |
0,00534 |
|
UNTR |
0,0550 |
0,0357 |
1,7529 |
-0,0338 |
0,02116 |
|
ADHI |
0,0550 |
0,0357 |
2,1284 |
-0,0411 |
0,01392 |
|
BSDE |
0,0550 |
0,0357 |
1,8970 |
-0,0366 |
0,01838 |
|
KLBF |
0,0550 |
0,0357 |
1,5744 |
-0,0304 |
0,02461 |
Formula pada persamaan (2.8) menyatakan bahwa tingkat keuntungan yang diharapkan dari suatu saham adalah sama dengan tingkat keuntungan bebas resiko ditambah dengan premi risiko (yaitu (Rm — R)ββj). Semakin besar risiko saham (beta) tersebut, semakin tinggi premi risiko yang diharapkan dari saham tersebut. Dengan demikian semakin tinggi pula tingkat keuntungan yang diharapkan untuk saham tersebut. Formula tersebut juga menunjukkan bahwa premi risiko yang diharapkan dari suatu saham dengan beta 0,5 adalah setengah premi risiko pasar, dan premi risko yang diharapkan untuk suatu investasi dengan beta 2,0 adalah dua kali premi risiko pasar. Dengan menggunkan beta yang ditaksir untuk beberapa jenis saham, kita bisa memperkirakan beberapa tingkat keuntungan yang diharapkan/disyaratkan untuk saham-saham tersebut. Dari taksiran di atas untuk tingkat keuntungan yang diharapkan dari Beta CAPM-GARCH terlihat saham Bumi Serpong Damai Tbk adalah saham paling berisiko dengan beta 1,7841 dan return 0,02057 , dan untuk Beta CAPM-EGARCH saham Indofood CBP Sukses Makmur (Tbk) adalah saham yang paling berisiko dengan beta 2,5729 dan return 0,00534. Sedangkan tingkat yang diharapkan pasar sebesar 0,0357 yang artinya saham-saham tersebut memiliki tingkat keuntungan yang diharapkan lebih kecil dari pasar (Underpriced), artinya jika pasar naik 0,01 maka saham akan naik 0,01. Jadi β menunjukkan kepekaan perubahan kelebihan keuntungan suatu saham, semakin besar β terhadap return CAPM, semakin besar pula premi risiko tersebut.
Hasil perbandingan dapat ditarik kesimpulan bahwa apabila beta suatu saham semakin agresif maka semakin besar resiko (beta > 1) yang dimiliki saham tersebut. Beta secara individu mempengaruhi return saham.
Disini terlihat dari beta GARCH saham Bumi Serpong Damai tbk (Persero) (BSDE) merupakan beta tertinggi yaitu 1,7841 sedangkan dari beta EGARCH saham Indofood
CBP Sukses Makmur Tbk (ICBP) yang paling agresif yaitu 2,5729. Untuk CAPM-GARCH saham KLBF sebesar 0,02866 dengan beta sebesar 1,3660 dan CAPM-EGARCH saham KLBF sebasar 0,02461 dengan beta sebesar 1,5744 yang artinya saham KLBF menggunakan model CAPM-GARCH yang baik karena return yang diharapkan besar dan risikonya kecil.
Dari model CAPM dapat ditaksir tingkat keuntungan yang diharapkan saham lebih besar dari tingkat keuntungan yang diharapkan pasar, yang artinya saham-saham terlalu berisiko. Ke 6 saham tersebut termasuk saham-saham agresif.
Adapun hal-hal yang disarankan peneliti untuk dapat dijadikan pertimbangan dalam penelitian selanjutnya yaitu:
-
1. Metode CAPM dapat digunakan sebagai dasar pertimnbangan untuk melakukan investasi di pasar modal.
-
2. Untuk memiliki investasi yang efisien, investor harus memiliki beberapa alternatif asset yang dapat menunjang pengurangan resiko,seperti portofolio dll.
-
3. Penelitian ini hanya menghitung kinerja saham dengan dua metode saja yaitu CAPM GARCH dan CAPM EGARCH. Besar harapan penulis adanya penelitian berikutnya yang menggunakan model pendekatan lainnya seperti T-GARCH, EGARCH-M, GJR.
DAFTAR PUSTAKA
Engle, R.F, 1982. “Autoregressive Conditional Heteroscedasiticity with Estimates of the Variance of U.K. Inflation.
Econometrica.Vol 50, No. 4, Hal 898.
Husnan, Suad, 2005. Dasar-dasar Teori Portofolio dan Analisis Sekuritas. Edisi Keempat. Yogyakarta: UPP AMP YKPN.
Huang, J., et al. 2010. Estimating value at risk of portfolio by conditional copula-GARCH method. Insurance: Mathematics and
Economics
Pradipta , I Gusti Ayu D, 2010. Perhitungan Risiko Sistematis Saham Menggunakan
CAPM-GARCH. Skripsi. Universitas
Udayana.
Rosadi, Dedi, 2011. Analisis Ekonometrika dan Runtun Waktu Terapan dengan R. Yogyakarta.
Tsay, R. S. 2002. Analysis of Financial Time Series: Financial Econometrics. John Wiley & Sons, Inc. New York.
Widiyati, Nur. 2009. Penerapan Model GARCH dan Model EGARCH pada Saham Sektor Properti Ketika Krisis Ekonomi Dunia. Skripsi.
247
Discussion and feedback