E-Jurnal Matematika Vol. 6 (4), November 2017, pp. 226-232

DOI: https://doi.org/10.24843/MTK.2017.v06.i04.p170

ISSN: 2303-1751

APLIKASI MODEL MEAN REVERSION DENGAN MUSIMAN DALAM MENENTUKAN NILAI KONTRAK OPSI TIPE EROPA PADA HARGA KOMODITAS KAKAO

Ida Ayu Putu Candra Dewi1§, Komang Dharmawan2, Ni Made Asih3

1Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected] ] 2Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected] ] 3Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

§Corresponding Author

ABSTRACT

Many literatures explain that commodity prices tend to follow the pattern of Mean Reversion models, commodity prices are controlled by seasonal supplies resulting in price fluctuations. To overcome the risk of fluctuations in the price, an investor can hedge with option contracts. The purpose of this research was to know the application of Mean Reversion model with seasonal in determining the value of European option contract from commodity ,by estimating the parameters and simulating the model in order to get the value of European option contract. Thus, the values of the options obtained with the model was compared with the value of the options calculated by the Black-Scholes model. The results of this study indicated that the value of contract option of Mean Reversion model with seasonal value was lower than the Black-Scholes model.

Keyword: Mean Reversion, Seasonal, European Type Option Contract, Black-Scholes

  • 1.    PENDAHULUAN

Derivatif merupakan suatu kontrak keuangan antar dua pihak untuk mentransaksikan suatu aset dengan berbagai hal yang telah disepakati bersama saat ini, tetapi akan direalisasikan nanti pada tanggal (dalam kurun waktu) tertentu di masa yang akan datang (Siahaan, 2008). Pasar keuangan derivatif dapat dikelompokkan berdasarkan kontrak, salah satunya adalah kontrak opsi. Kontrak opsi (option contract) merupakan suatu kontrak yang memberikan hak kepada pemegangnya, namun bukan kewajiban untuk membeli (atau menjual) suatu aset pada harga yang telah ditentukan sebelumnya dalam jangka waktu tertentu (Brigham dan Houston, 2011).

Induk instrumen dalam derivatif tidak terbatas pada aktiva finansial saja, seperti saham, warrants, dan obligasi, tetapi juga pada komoditas. Popularitas komoditas pertanian di kalangan investor di pasar saham telah berkembang sejak tahun 2000. Hal ini

disebabkan oleh tuntutan diversifikasi portofolio dan meningkatnya permintaan untuk kebutuhan komoditas pertanian, seperti minyak kelapa sawit, kakao, kopi, dan lain-lain (Dharmawan, 2016). Harga komoditas pertanian ataupun perkebunan (kedelai, gandum, kopi, kakao) digerakkan oleh pasokan musiman, umumnya harga akan lebih tinggi sebelum musim panen (Barakova & Geman, 2006), karena komoditas perkebunan diproduksi secara musiman, tetapi dikonsumsi sepanjang tahun. Hal ini berpengaruh terhadap ketidakseimbangan antara persediaan dan permintaan yang akan menyebabkan harga komoditas berfluktuatif. Oleh karena itu, seorang investor diharapkan memiliki suatu perencanaan dalam menghadapi risiko fluktuasi harga dengan melakukan lindung nilai (hedging) menggunakan kontrak opsi.

Opsi dapat digunakan untuk meminimalkan risiko dan memaksimalkan keuntungan dengan daya ungkit (leverage) yang lebih besar (Siahaan, 2008). Model yang dapat digunakan

dalam penentuan kontrak opsi salah satunya adalah model Mean Reversion. Model ini menyatakan bahwa harga akan cenderung kembali ke tingkat nilai rata-rata.

Berdasarkan uraian pada bagian terdahulu, peneliti tertarik mengaplikasikan model Mean Reversion dengan musiman dalam penentuan nilai kontrak opsi Eropa pada harga komoditas kakao. Untuk mengetahui kinerja model Mean Reversion musiman, maka nilai opsi Eropa yang diperoleh dibandingkan dengan nilai opsi dari model Black-Scholes. Black-Scholes merupakan model perhitungan kontrak opsi Eropa standar yang umumnya banyak digunakan oleh masyarakat keuangan untuk menilai apakah harga opsi yang terjadi di pasar sudah merupakan harga yang dianggap fair bagi opsi tersebut (Tandelilin, 2010).

  • 2.    METODE PENELITIAN

Data yang digunakan dalam penelitian ini adalah data sekunder berupa data harian historis harga komoditas kakao selama empat tahun terakhir, yaitu dari 3 Januari 2011 sampai dengan 31 Mei 2017. Dalam penelitian ini penulis mengambil data komuditas kakao dari situs https://www.investing.com.

Berikut merupakan langkah-langkah dalam menentukan nilai kontrak opsi call tipe Eropa komoditas kakao menggunakan Mean Reversion dengan musiman :

  • 1.    Mengumpulkan data historis dari harga komoditas kakao.

  • 2.    Menghitung tingkat pengembalian (return) dari data historis harga komoditas kakao dengan persamaan

R‘='"(⅛)          (1)

  • 3.    Menghitung nilai masukan deskriptif statistik rata-rata data (mean), ragam data (variance), simpangan baku   (standar

deviation), kemiringan data (skewness), dan kurtosis dari data return komoditas kakao.

  • 4.    Mengestimasi nilai parameter dari Mean Reversion dengan persamaan berikut menggunakan Least Square Method, sehingga diperoleh μ, σ,dan k.

dXt = κ(μ - Xt) dt + σdWt      (2)

  • 5.    Mengestimasi nilai parameter deterministik f(t) dengan least square method

  • 6.    Setelah diperoleh parameter Mean Reversion dan musiman, maka akan dibentuk harga komoditas kakao dari model Mean Reversion dengan musiman

  • 7.    Setelah model umum diperoleh, maka akan dihitung harga komoditas kakao dari model Mean Reversion dengan musiman

  • 8.  Menghitung nilai kontrak Opsi Call Tipe

Eropa komoditas kakao dari Mean Reversion dengan musiman dengan persamaan

  • 9.    M       C = e~rτ maks(Sτ-K,0)         (3)

e

nghitungan nilai kontrak Opsi Call Tipe Eropa menggunakan model Black-Scholes dengan persamaan

C = S0N(d1) - Ke~rtN(d2)       (4)

  • 10.    Membandingkan nilai kontrak Opsi Call tipe Eropa model Blackscholes dan Mean Reversion dengan musiman.

  • 3.    HASIL DAN PEMBAHASAN

Pada penelitian ini data yang digunakan adalah data historis dari komoditas kakao periode 3 Januari 2011 sampai 31 Mei 2017. Gambar 1 menunjukkan bahwa terjadi fluktuasi harga pada komoditas kakao yang dapat ditunjukkan dalam bentuk Grafik.

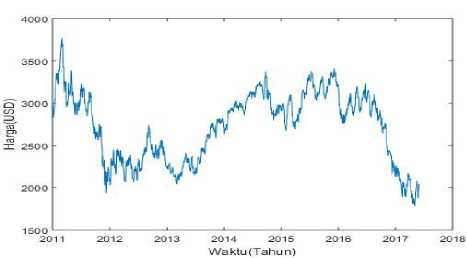
Gambar 1. Grafik harga komoditas kakao periode 3 Januari 2011 sampai 31 Mei 2017

  • 3.1    Menghitung Tingkat Pengembalian

(Return)

Menentukan nilai R^ (Return kakao pada waktu ke-t) diperoleh dengan menggunakan persamaan (1). Sebagai contoh, t=1 diperoleh dengan sebagai berikut:

2932

R1 =ln(3021)

= -0,0299

dengan cara yang sama, dapat dihitung nilai R^ dengan    1≤t ≤ 1623    menggunakan

persamaan (1).

  • 3.2    Karakteristik Data

Karakteristik data diketahui dengan melihat nilai statistik deskriptif dari data tingkat pengembalian (return) harga komoditas kakao. Dalam proses ini nilai statistik deskriptif diperoleh dengan mengitung nilai mean, variance, standar deviation, skewness, dan kurtosis. Sehingga diperoleh hasil yang dapat dilihat pada Tabel 1.

Tabel 1. Nilai Statistik Deskriptif Data Masukan

Variabel Deskriptif

Nilai

Mean

-0,0002

Variance

0,07045

Standar deviation

0,2654

Skewness

-0,0909

Kurtosis

3,3658

Tabel 1 menunjukkan bahwa data return komoditas kakao memiliki bentuk yang tidak simetris yang dapat ditunjukkan dengan karakteristik data yang memiliki nilai skewness negatif yang mengakibatkan data menceng (skew) ke kiri dan memiliki ekor gemuk (fat tail) dilihat dari nilai kurtosis yaitu 3,3658 >3, hal ini menunjukkan sebaran data tidak normal dikarenakan pada waktu tertentu harga komoditas kakao dapat melonjak naik ataupun turun.

  • 3.3    Variabel-variabel Penentuan Nilai

    Kontrak Opsi

Dalam menentukan nilai kontrak opsi call tipe Eropa terdapat beberapa variabel-variabel yang digunakan yaitu 1^O (harga saham awal), ^T (harga komoditas saat jatuh tempo), K(harga tebus), r (suku bunga bebas risiko yang dikeluarkan oleh Bank Indonesia), dan T (Waktu jatuh tempo opsi). Nilai ¾ dapat dilihat pada data historis komoditas kakao 31 Mei 2017 yaitu sebesar USD 2,048. Waktu jatuh tempo opsi ditentukan selama tiga bulan, sedangkan untuk suku bunga bebas risikonya sebesar 6.5% yang dikeluarkan oleh Bank Indonesia. Harga pelaksanaan disepakati antara penjual dan pembeli opsi yang ditentukan sebesar USD 2,100 , USD 2,125 dan USD 2,150 USD.

  • 3.4    Mengestimasi Nilai Parameter dari Mean Reversion

Mean Reversion merupakan suatu model yang telah berperan dalam bidang ekonomi dan finansial, khususnya digunakan dalam menentukan gerak harga komoditas yang terkenal adalah Ornstein-Uhlenbeck Process atau yang sering dikenal dengan Vasicek Process. Proses simulasi model Mean Reversion yang terdapat pada persamaan (2), menurut (Smith, 2010) jika menggunakan data waktu diskrit maka dapat dimodelkan sebagai

Xt =  ∆t+(1-K∆t)Xt^1 +σ∆ Wt   (5)

Pada penelitian ini, parameter-parameter Mean Reversion diestimasi dengan metode Least Square, sehingga diperoleh parameter ̂, ̂, dan ̂ seperti pada Tabel 2

Tabel 2 Parameter-Parameter Mean Reversion

Parameter

Nilai

̂

0,000462

̂

2,596

̂

0,2635

  • 3.5    Nilai Parameter Deterministik f(t)

Nilai Parameter Musiman deterministik f(t) diestimasi menggunakan metode least square. Model musiman komoditas kakao pada penelitian ini, diperoleh dengan menyesuaikan periode-periode yang sesuai dengan pergerakan dari harga komoditas kakao. Model yang pernah diusulkan oleh (Seifert & Homburg, 2007) digunakan sebagai acuan untuk membentuk sebuah model pergerakan harga musiman dari komoditas kakao sehingga pada penelitian ini diperoleh model pergerakan harga musiman dari komoditas kakao pada persamaan berikut :

f(t)=sI sin(0,75πt)+S2 cos(0,9πt)+

$3 sin(0,65πt)+S4 cos(0,75πt)+S5 (6)

Model pada persamaan (6), digunakan untuk mengestimasi parameter musiman yaitu ̂, ̂,̂, ̂,dan ̂ dengan menggunakan metode least square sehingga diperoleh hasil yang dapat dilihat pada Tabel 3.

Dengan diperolehnya model dan parameter dari musiman, maka diperoleh plot harga musiman komoditas kakao yang ditampilkan pada Gambar 2.

  • 3.6    Model Mean Reversion dengan

    Musiman

Harga komoditas kakao pada penelitian ini diperoleh dengan menggabungkan model Mean Reversion dan model musiman yang telah diperoleh. Jika Sfc merupakan harga komoditas kakao model Mean Reversion dengan musiman pada waktu t, maka harga komoditas kakao dapat dimodelkan sebagai

ln(St)=Xt +f(t) atau, ekuivalen dengan

St = exp(xt +f(t))

dengan S t merupakan harga kakao saat waktu t dari model Mean Reversion dengan musiman, Xt merupakan proses Mean Reversion pada persamaan (5) dan f(t) merupakan model musiman komoditas kakao pada persamaan (6) yang diasumsikan deterministik.

Tabel 3. Estimasi Parameter Musiman Komoditas Kakao

Parameter

̂

̂

̂

̂

̂

Value

-0,1893

-0,1046

0,2783

0,2544

7,9042


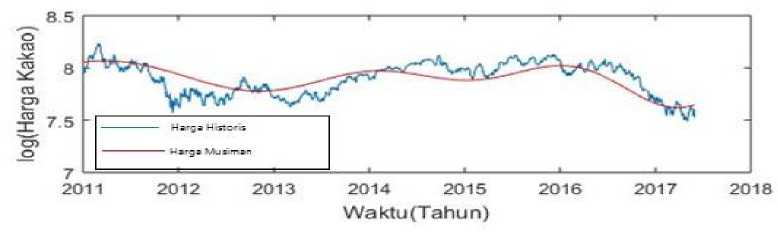
Gambar 2. Grafik Logaritma Harga dan Musiman Harga Kakao Periode 03 Januari 2011

Sampai 31 Mei 2017


  • 3.7    Penentuan Nilai Kontrak Opsi Menggunakan Simulasi Model Mean Reversion dengan Musiman

Penentuan nilai kontrak opsi call Eropa komoditas kakao dari model Mean Reversion dengan musiman, diperoleh dengan melakukan proses simulasi untuk memperoleh harga komoditas kakao saat jatuh tempo (Sr).

Proses simulasi dilakukan dengan mensubstituisi nilai-nilai parameter model Mean Reversion dan musiman f (t) pada persamaan (5) dan persamaan (6). Proses simulasi Mean Reversion dilakukan sebanyak 100.000 kali simulasi sampai Bulan Desember 2017, untuk melihat pergerakan harga komodita hingga akhir tahun 2017. Kemudian model dari musiman f(t) ditambah setelah simulasi. Dari sini diperoleh plot harga kakao dari simulasi model Mean Reversion dengan musiman. pada Gambar 3 dan Gambar 4

menunjukkan bahwa, simulasi yg dilakukan 10 kali selama akhir tahun 2017, menghasilkan pergerakan harga komoditas (St) yang memiliki tren naik dan harga simulasi sesuai dengan gerak musimannya.

Penentuan nilai kontrak opsi call tipe Eropa, diperoleh dengan mensubstitusi harga St yang merupakan harga komoditas saat jatuh tempo kakao selama 3 bulan dengan nilai K, r dan T yang sudah ditentukan ke dalam persamaan (3). Selanjutnya, nilai yang diperoleh dirata-ratakan sehingga, nilai opsi call dari komoditas kakao Pada Tabel 4 memperlihatkan nilai kontak opsi call tipe Eropa dengan jumlah simulasi 10 kali, 100 kali, 1.000 kali, 10.000 hingga 100.000 kali dengan menggunakan bantuan program Matlab.

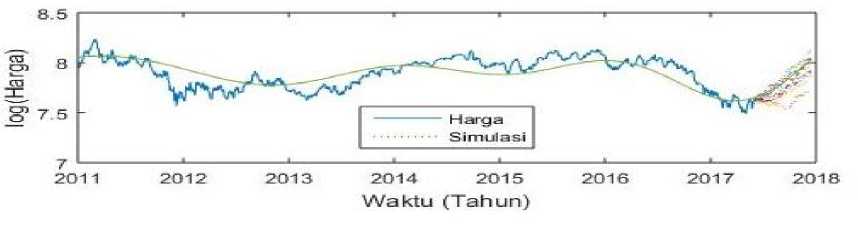
Gambar 3. Grafik Logaritma Harga dengan Musiman Kakao 03 Januari 2011 sampai 31 Mei 2017 dan Simulasi Logaritma Harga Model Mean Reversion dengan


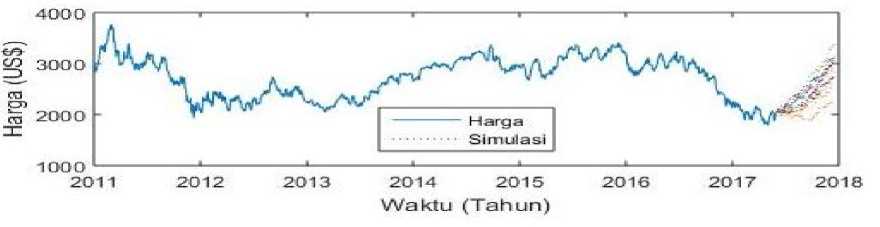
Gambar 4. Grafik Harga dengan Musiman Kakao 03 Januari 2011 sampai 31 Mei 2017 dan

Simulasi Harga Model Mean Reversion dengan Musiman Kakao selama 7 Bulan


Tabel 4. Nilai Kontrak Opsi Call Tipe Eropa Komoditas Kakao Mean Reversion dengan Musiman

Harga Tebus (K) (USD)

Simulasi

Harga call opsi tipe Eropa (USD)

2,100

10

97.6565

100

98.3385

1.000

99.4962

10.000

99.9297

100.000

99.9084

2,125

10

80.1429

100

82.8514

1.000

84.0655

10.000

84.8605

100.000

84.8018

2,150

10

69.7337

100

69.0436

1.000

70.3656

10.000

70.4432

100.000

70.4308

  • 3.8    Penentuan Nilai Kontrak Opsi Black-Scholes

Penentuan harga opsi harga komoditas (S t ) yang dihitung menggunakan model Black-Scholes diperoleh dengan mensubstitusi nilai S0 ,K,r,T dan σ dari nilai standar deviation data historis kakao yang sudah diperoleh pada persamaan (4), yaitu:

ln( 0)+(r+0,5σ2)(t)

d1=

σ√t

2048            0,26542

ln (2100) + (0,065 +   2   ) 0,25

0,2654√0,25

= -0,00014

dengan demikian diperoleh nilai ^2

⅛ =  -σ√t

= -0,00014 - 0,2654

= -0,13284

selanjutnya dihitung nilai N(d1)dan N(cL^ ) yang digunakan untuk menghitung nilai kontrak opsi call tipe Eropa, nilai N(d1)dan N( ^■2 )   yang telah didapat

disubstitusi kedalam persamaan (4), sehingga diperoleh:

C = 2048 (0,499943) - 2100e( -o , 065 ×0, 25)(0,447159) = 99,9857

dengan cara yang sama diperoleh nilai kontrak opsi tipe Eropa Black-Scholes dari setiap Harga Tebus (K) yang ditampilkan pada Tabel 5.

Tabel 5. Nilai kontak opsi call tipe Eropa

Black-Scholes

Harga Tebus (K) (USD)

Nilai kontak opsi call tipe Eropa Black-Scholes (USD)

2,100

99.9857

2,125

89.4195

2,150

79.7016

  • 3.9    Perbandingan Hasil Harga Model Mean Reversion dengan Musiman dan Model Black-Scholes

Berdasarkan kedua hasil model pada Tabel 6 menunjukkan, nilai kontrak opsi Eropa yang dihitung untuk beberapa harga tebus (K) menggunakan model Mean Reversion dengan musiman, dapat menghasilkan harga yang lebih rendah dari model Black-Scholes. Nilai opsi kedua model tersebut menunjukkan bahwa semakin tingginya harga tebus dari sebuah opsi, maka semakin rendah nilai call dari opsi tersebut.

Tabel 6. Perbandingan Nilai kontrak Opsi

Call Tipe Eropa Menggunakan Mean Reversion dengan Musiman dan Black-Scholes

Harga Tebus (K) (USD)

Nilai kontak opsi call tipe Eropa Mean Reversion dengan musiman (USD)

Nilai kontak opsi call tipe Eropa Black-Scholes (USD)

2,100

99.9084

99.9857

2,125

84.8018

89.4195

2,150

70.4308

79.7016

  • 4.    KESIMPULAN DAN SARAN

Perbandingan nilai, kontrak opsi call tipe Eropa komoditas kakao yang dihitung menggunakan model Mean Reversion dengan musiman, menghasilkan harga yang lebih rendah dari model Black-Scholes, dan model Mean Reversion dengan musiman melibatkan lebih banyak parameter dari model Black-Scholes.

Berdasarkan hasil yang telah diperoleh, adapun saran untuk pengembangan penelitian selanjutnya yaitu, model ditambahkan dengan jump dengan volatilitas bersifat stokastik dan suku bunga bebas risiko yang berbeda-beda untuk menyesuaikan dengan keadaan pasar.

DAFTAR PUSTAKA

Barakova, S. & Geman, H., 2006. Seasonal

and Stochastic Effects in Commodity

Forward Curves. Review of Derivative Research, Volume 9, p. 167-18.

Brigham & Houston, 2011. Essentials of FInancial Management.Edisi 11. Salemba empat,Jakarta.

Dharmawan, K., 2016. Pricing European

Options on Agriculture Commodity Prices

Using Mean-Reversion Model with Jump Diffusion. Jawa Barat, Indonesia.

Dixit & Pindyck, 1994. Investment under

Uncertainty. s.l.:Princeton University

Press,41 William Street,Princeton, New Jersey 08540.

Seifert, J. & Homburg, U.-.  M.,  2007.

Modelling Jumps in Electricity Prices:

Theory and Empirical Evidence. Review of Derivatives Redearch , Volume 10, pp. 59-85.

Siahaan, H., 2008. Seluk Beluk Perdagangan Instrumen Derivatif. Jakarta: PT Elex Media Kumputindo.

Smith, W., 2010. On the Simulation and

Estimation of the Mean-Reverting.

Commodities Market and Modelling.

Tandelilin, E., 2010. Portofolio Dan Investasi

Teori Dan Aplikasi. Kanisius.

232