APLIKASI MODEL REGRESI SEMIPARAMETRIK SPLINE TRUNCATED (Studi Kasus: Pasien Demam Berdarah Dengue (DBD) di Rumah Sakit Puri Raharja)
on
E-Jurnal Matematika Vol. 6 (1), Januari 2017, pp. 65-73
ISSN: 2303-1751
APLIKASI MODEL REGRESI SEMIPARAMETRIK SPLINE TRUNCATED
(Studi Kasus: Pasien Demam Berdarah Dengue (DBD) di Rumah Sakit Puri Raharja)
Ni Wayan Merry Nirmala Yani1, I Gusti Ayu Made Srinadi2§, I Wayan Sumarjaya3
1Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: merrynirmala72@gmail.com] 2Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: srinadi@unud.ac.id 3Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id]
ABSTRACT
Semiparametric regression is a regression model that includes parametric components and nonparametric components in a model. The regression model in this research is truncated spline semiparametric regression with case studies of patients with Dengue Hemorrhagic Fever (DHF) at Puri Raharja Hospital during the period of January to March 2015. The best regression model estimation is obtained from the selection of optimal knots which has minimum Generalized Cross Validation (GCV) is. Parametric components in this research include age (years), body temperature (0C), platelets (× 10/μL), and hematocrit (%) as a nonparametric component. The minimum value of GCV is 0.03552045 achieved at the point of 39.6 knots, MSE value of 0.0296922; and the value of coefficient determination is 98.91%, obtained from semiparametric regression model truncated linear spline (order 2) with a single point of knots.
Keywords: GCV, knots, semiparametric regression, spline
pendekatan histogram, estimator kernel, estimator deret orthogonal, analisis wavelet, estimator MARS, estimator deret Fourier, estimator spline dan lain-lain. Pendekatan spline memiliki suatu basis fungsi, di mana basis fungsi yang biasa digunakan antara lain spline truncated dan B-spline (Lyche, et al., 2008).
Spline adalah salah satu jenis piecewise polynomial (Eubank, 1988). Maksud piecewise polynomial adalah polinomial yang memiliki sifat tersegmen atau sifat terpotong-potong. Model polinomial dengan sifat tersegmen menyebabkan spline memiliki fleksibilitas yang lebih tinggi dari model polinomial biasa, sehingga menyebabkan regresi spline dapat menyesuaikan diri secara lebih efektif terhadap karakteristik lokal suatu fungsi data atau dengan kata lain regresi spline dapat menghasilkan suatu fungsi regresi yang sesuai dengan data.
Apabila pada sebuah model regresi terdapat komponen model yang diestimasi secara parametrik dan komponen lain menggunakan
pendekatan nonparametrik terbentuklah model regresi semiparametrik. Penelitian sebelumnya mengenai pemodelan menggunakan regresi semiparametrik spline pernah dilakukan oleh Marina & Budiantara (2013) yang memodelkan faktor-faktor yang memengaruhi persentase kriminalitas di Jawa Timur dengan pendekatan regresi semiparametrik spline. Laome (2009) memodelkan regresi semiparametrik spline untuk data longitudinal pada kadar CD4 penderita HIV. Sugiantari & Budiantara (2013) meneliti analisis faktor-faktor yang
memengaruhi angka harapan hidup di Jawa Timur menggunakan regresi semiparametrik spline. Wibowo et al. (2013) yang meneliti
estimasi parameter dalam regresi
semiparametrik spline. Regresi semiparametrik spline truncated digunakan dalam penelitian ini dengan studi kasus pasien Demam Berdarah Dengue (DBD) di Rumah Sakit Puri Raharja yang diambil dari penelitian Fitriani (2015).
Penelitian ini bertujuan menentukan estimasi model regresi semiparametrik dengan spline truncated pada data pasien DBDdi Rumah Sakit Puri Raharja dan mengetahui variabel-variabel apa saja yang berpengaruh signifikan.
independen dan bersifat acak dengan nilai tengah nol dan variansi σ 2 dalam amatan ke-i, dan adalah banyaknya amatan Model antara dua atau lebih variabel independen atau variabel prediktor (X1, X2 ,X3 ,-,Xh) dengan variabel dependen ( ) secara umum dapat ditulis sebagai berikut (Neter, et al., 1990):
Yi =∑=OXg Xig+ε i (2.2)
dengan i = 1,2,3,...,n; /oJi,Y2,-,Yh adalah parameter koefisien regresi, Xt 1 ,Xt 2 ,-,Xt h
adalah peubah bebas yang diketahui nilainya, dan tt adalah galat atau sisaan yang saling bebas atau independen yang berdistribusi normal dengan nilai tengah nol dan variansi dalam amatan ke-i.
Adapun koefisien determinasi dalam regresi
parametrik adalah sebagai berikut (Neter, et al.,
1990):
r2 =JKR = I-JKG
JKT JKT
(2.3)
Pengujian parameter model secara serentak (simultan) dilakukan dengan menggunakan uji F. Adapun hipotesis pada uji F ini adalah sebagai berikut (Neter, et al., 1990):
H0: Yi = Y2 = ∙∙∙ = Yh = 0,
: tidak semua sama dengan nol
Adapun statistik uji yang digunakan pada uji
F adalah sebagai berikut:
r h 1 tung κτg jkg ∣
(2.4)
dengan keputusan tolak H0 jika Fhitung ≥ Fa; ((p+1 ) - 1,n -(p+1)) atau p-value< Ct-Sedangkan Pengujian parameter model secara parsial (individu) yaitu menggunakan uji
-
t. Adapun hipotesis yang digunakan dalam uji t adalah sebagai berikut (Neter, et al., 1990):
H0: Yg = 0,
Hi: Yg ≠0 ;g = 1,2, - ,X
Adapun statistik uji yang digunakan pada uji adalah sebagai berikut:
v„
th iturιg = ^j (2-5)
dan tolak H0 jika ∖⅛ itung∖ > t— -(p+1 ); dengan
n merupakan jumlah pengamatan dan (p + 1) merupakan banyaknya parameter.
Residual (goodness of fit) dari suatu model regresi harus memenuhi asumsi IIDN(Q,σ2) yaitu identik, independen, dan berdistribusi normal. Pemeriksaan asumsi homogenitas atau uji asumsi identik dapat dilakukan dengan menggunakan uji Glejser (Gujarati, 2006). Pada uji Glejser mempertimbangkan regresi nilai |ej, terhadap variabel X yang dianggap berhubungan dekat dengan varians heteroskedastisitas σ2. Sementara itu asumsi residual independen dapat dilakukan dengan menggunakan uji d Durbin-Watson, adapun uji d Durbin-Watson dapat dirumuskan sebagai berikut (Gujarati, 2006):
d = ∑^3^ (2.6)
Sedangkan pengujian asumsi normalitas dapat dilakukan dengan melakukan uji Anderson-Darling. Adapun uji Anderson-Darling dapat dirumuskan sebagai berikut (Anderson & Darling, 1954):
A2 = -n-S (2.7)
dengan S = ^∑^ 1[2i - 1] [log(F(Zi)) +
log(1 — F(Z++1 _ j))] adalah simpangan baku data, Zi = —^- adalah data Xi yang
distandarisasi, Xj adalah data ke-i yang telah diurutkan, X adalah rata-rata data, F(Zi) adalah nilai fungsi distribusi kumulatif normal baku di , adalah statistik uji untuk metode
Anderson-Darling, n adalah ukuran sampel, dan F0 (X) adalah fungsi distribusi kumulatif teoritis.
Secara umum model regresi nonparametrik dapat dinyatakan sebagai berikut (Eubank, 1988):
Yi =f (t) + εi ; i = 1,2,3.....n (2.8)
dengan adalah nilai peubah respons dalam amatan ke-i, adalah variabel bebas atau
variabel prediktor, adalah suku galat atau sisaan yang diasumsikan independen dan
bersifat acak dengan nilai tengah nol dan variansi , dan ( ) adalah regresi yang tidak diketahui bentuk atau polanya.
Regresi spline merupakan salah satu teknik estimasi dalam regresi nonparametrik dengan model polinomial yang memiliki sifat tersegmen atau terpotong-potong yang mulus. Apabila regresi ( ) pada persamaan (2.8) dihampiri
fungsi spline, maka untuk mengestimasi f (t i) dapat digunakan dengan model regresi spline. Secara umum model regresi spline pada suatu fungsi dengan orde dapat dinyatakan sebagai berikut (Eubank, 1988):
f (ti) = ∑⅛ βi1{ + ∑F= 1% _ 1+i^i — W 1
(2.9) dengan β0 ,β1 ,β2 ,...,βp _ 1 ,β(p _ 1+i) adalah
parameter koefisien regresi, 1i ,12,.,1i
adalah peubah bebas yang diketahui nilainya, adalah banyaknya titik knot X1 ,K2,K3,.,Kr , dan ( — )
(truncated) yang
berikut:
( t —k+- 1 = {(11
adalah fungsi potongan dapat diuraikan sebagai
— K)~ 1 , 11≥ K1
0 , ιi< κl.
(2.10)
Apabila persamaan (2.8) disubsitusikan ke dalam persamaan (2.9) maka akan diperoleh persamaan regresi nonparametrik spline truncated sebagai berikut:
Yt = ∑pj-0βpi1i+∑r= 1% _ 1+)di —
Ki)++- r + ε i. (2.11)
dengan i = 1,2,3,..., n.
Regresi semiparametrik merupakan
gabungan antara regresi parametrik dan regresi nonparametrik. Secara umum model regresi semiparametrik dapat dinyatakan sebagai berikut (Ruppert , et al., 2003):
Yi =f (t)+X^ γ + εi (2.12)
dengan i = 1,2,3, ...,n , Yi adalah nilai variabel respons dalam amatan ke-i,
= ( , , ,., ) adalah peubah bebas
atau variabel prediktor yang berhubungan secara
parametrik dengan variabel respons Yi, γ = (Yo,Y1,Y2, -,Yh) adalah parameter koefisien regresi,Sementara itu ti adalah variabel prediktor yang tidak diketahui bentuk polanya terhadap variabel respons (berhubungan secara nonparametrik dengan variabel respons Yi). Apabila model persamaan (2.2) dan (2.9) disubstitusikan ke persamaan (2.12), sehingga diperoleh:
Yt ∑j 1κ t j ∙∑r 1% - 1+0( ti-
Kl )p+- 1+∑^ = γYg Xig +Zi (2.13)
Titik knot merupakan titik perpaduan bersama yang memperlihatkan terjadinya perubahan perilaku dari fungsi spline pada interval-interval yang berbeda sehingga kurva yang terbentuk tersegmen pada titik tersebut. Pada penentuan model regresi spline dapat dilakukan dengan melihat nilai Generalized Cross Validation (GCV) yang minimum. Adapun rumus untuk menghitung GCV adalah sebagai berikut (Eubank, 1988):
G CV (K) =
MSE (K') (n~ 1tr[I -Tl(K)])2
(2.14)
dengan MSE(K) = n 1 ∑∙L 1 (Yi - f(ti)) , K adalah titik knot (K1, K2 ,K3 ,...,Kn), f (t i) = t (t' t)- 11 'Y, n adalah jumlah data, I adalah matriks identitas, A(K) = (tt' t)- 11 ', dan Yi = A(K) Y.
Penyakit DBD yang disebabkan oleh virus dengue yang termasuk kelompok B Arthropod virus yang dikenal sebagai genus Flavivirus dengan family Flaviviride. Virus dengue mempunyai empat jenis serotype yaitu DEN-1, DEN-2, DEN-3 dan DEN-4. Terdapat tiga faktor pemegang peran dalam penularan infeksi virus dengue yaitu manusia, virus, dan vektor perantara. Virus dengue yang menular ke manusia ditularkan oleh gigitan nyamuk Aedes aegypty (Departemen Kesehatan Republik Indonesia 2004).
Jenis data yang digunakan adalah data sekunder yaitu pasien DBD yang menjalani rawat inap di Rumah Sakit Puri Raharja Denpasar dengan sampel data rekam medis pasien Demam Berdarah Dengue (DBD) sebanyak 70 sampel periode bulan Januari sampai bulan Maret 2015 yang diambil dari penelitian Fitriani (2015).
Variabel penelitian yang digunakan terdiri dari satu variabel respons dan tujuh variabel yang diduga berpengaruh Adapun variabel respons yang digunakan yaitu lama kesembuhan pasien (hari), jenis kelamin, umur (tahun), suhu tubuh (0C), nadi (X/m e n i) , lama demam (hari), jumlah trombosit (× 10 V^l), dan kadar kematokrit (%). Teknik analisis data dalam model regresi semiparametrik spline truncated adalah sebagai berikut:
-
1. Menetapkan komponen parametrik dan
komponen nonparametrik berdasarkan penelitian sebelumnya yang dilakukan oleh Fitriani (2015).
-
2. Memilih titik knot optimal dengan
menggunakan Generalized Cross Validation (GCV) yang paling minimum.
-
3. Memodelkan data lama kesembuhan pasien
DBD yang pernah menjalani rawat inap di Rumah Sakit Puri Raharja Denpasar (variabel respons) dengan variabel prediktor yang telah ditetapkan dengan regresi Semiparametrik Spline Truncated dengan titik knot optimal.
-
4. Menghitung nilai koefisien determinasi (R2 ).
-
5. Menguji signifikasi parameter regresi Semiparametrik Spline Truncated secara serentak dengan uji .
-
6. Melakukan uji parameter regresi Semiparametrik Spline Truncated secara parsial dengan uji .
-
7. Menguji asumsi residual IIDN dari model regresi Semiparametrik Spline Truncated.
-
8. Menginterpretasikan model, membandingkan hasil analisis yang di-peroleh dengan menggunakanan regresi semiparametrik
spline truncated terhadap estimasi regresi semiparametrik meng-gunakan estimator kernel uniform yang sebelumnya telah dianalisis oleh Fitriani (2015), dan menarik kesimpulan.
Gambaran umum data penelitian yaitu lama kesembuhan pasien DBD (hari) sebagai variabel respons dengan peubah bebas yaitu umur (tahun), suhu tubuh (0C), nadi (kali/menit), kadar hematokrit (%), trombosit (× 103∕μL), dan lama demam (hari) diringkas dalam statistika deskriptif pada Tabel 1.
Tabel 1. Statistika Deskriptif Data Pasien DBD
|
Yitnabcl |
Ringkasan Slarislik | |||
|
Mm |
Mais |
Mem |
SiDev | |
|
Ijim Ke-MJtiitahAiiiYi |
70 |
10.0 |
7.329 |
1.666 |
|
Salut iS) |
36,0 |
403 |
37.464 |
1,174 |
|
ι⅛∣w |
4.0 |
80.0 |
32,040 |
16.930 |
|
Luiu Ikiiuin ∣LD) |
1.0 |
9.0 |
3,700 |
1.397 |
|
Xatb IX) |
60.0 |
112.0 |
84,830 |
9.950 |
|
TιoπιbκiιιPLT) |
7.0 |
239.0 |
88.070 |
51.670 |
|
Kadar HenutokiK iH I Ci |
32.9 |
51.9 |
39,757 |
4.363 |
Penentuan komponen parametrik dan komponen nonparametrik ditentukan
berdasarkan informasi sebelumnya yang dilakukan oleh Fitriani (2015). Pada penelitian tersebut variabel umur, suhu tubuh, dan trombosit diasumsikan sebagai komponen parametrik dan variabel kadar hematokrit diasumsikan sebagai komponen nonparametrik sedangkan variabel lain yaitu lama demam dan nadi diasumsi tidak berpengaruh signifikan terhadap lama kesembuhan pasien yang sudah diwakili oleh variabel bebas lain yang signifikan.
-
4.3. Pemilihan Titik Knot Optimal Regresi
Semiparametrik Spline Truncated
Model yang dicobakan adalah regresi semiparametrik spline truncated dengan orde 2
dan orde 3, dengan satu knot, dua knot, dan tiga knot. Pemilihan titik knot optimal yang dicobakan adalah sebagai berikut.
-
a. Titik knot optimal regresi semiparametrik spline truncated linear (orde 2) dengan satu titik knot, diperoleh model sebagai berikut:
Yi = βo + βitii + β2(iιi - K))+ + /i %iι + ×2 xi2 + ×3 Xi 3 + ε i-
Nilai GCV minimum sebesar 0,03552 dicapai pada titik knot 39,6.
-
b. Titik knot optimal regresi semiparametrik spline truncated linear (orde 2) dengan dua titik knot, diperoleh model sebagai berikut:
Yi = βo + hi- i i + β2( t i i -
Xi)+ + β3( tii -
K2 ) + +/i xii + ×2 xi2 +
/3 Xi 3 + ε i-
Untuk model ini diperoleh nilai GCV minimum sebesar 0,03567 dicapai pada titik knot 39,7 dan titik knot 39,9.
-
c. Pemilihan titik knot optimal regresi semiparametrik spline truncated linear (orde 2) dengan tiga titik knot, diperoleh model sebagai berikut:
Y = β0 + βitii + β.2(tii - Xβ>+ +
β3( iii - X2) + +β4 (t[i - K3 )+ + hXii +
72 Xi2 + 73 Xi3 + εi∙
Dari model ini diperoleh nilai GCV minimum sebesar 0,03707 dicapai pada titik knot 34,1; titik knot 39,2; dan pada titik knot 47,7.
-
d. Pemilihan titik knot optimal regresi semiparametrik spline truncated kuadratik (orde 3) dengan satu titik knot, diperoleh model sebagai berikut:
Yi = β0 + βitii + β2tii + β3(tii - Ki)+ + YiXii + +/2Xi2 + Y3xi3 + εi -
Nilai GCV minimum sebesar 0,03632
dicapai pada titik knot 33,8.
-
e. Pemilihan titik knot optimal regresi
semiparametrik spline truncated kuadratik (orde 3) dengan dua titik knot, diperoleh model sebagai berikut:
Yi = + βltil + β2 t[i + β3 (tiι - Ki )+ +
β4 (til - Ki )+ + YiKu++Y2Kn + Y3Ki3 + Zi .
Untuk model ini diperoleh nilai GCV minimum sebesar 0,03682 dicapai pada titik knot 33,7 dan pada titik knot 40,5.
-
f. Pemilihan titik knot optimal regresi semiparametrik spline truncated kuadratik (orde 3) dengan tiga titik knot, diperoleh model sebagai berikut:
Yi = + βιtn + β2 tiι + β3 (tiι - Ki )+ +
β4 (til - K2 )+ + β3 (til - K3 )+ + YiKu++Y2Ki2 + Y3Ki3 + Zi .
Nilai GCV minimum sebesar 0,03795 dicapai pada titik knot 34,1; titik 35,2; dan pada titik 416,1.
Tabel 2. Nilai GCV dari Variasi Titik Knot dan Orde
|
Banyak Titik Knot |
Orde |
GCV |
|
1 tιtikknot 09«) |
orde2 |
0.03552 |
|
Ttitikknot 139." dan 39.91 |
orde2 |
O.O356^ |
|
3 titik knot (34.1:392: dan 47.7> |
ordε2 |
0.03707 |
|
1 Utik knot 03.81 |
orde 3 |
0.03632 |
|
2 tιtikknot (33.7 dan 4O.5⅛ |
orde3 |
0.03682 |
|
3 tιtikknot (34.1:35.5; dan 46.1) |
orde 3 |
0.03795 |
Dari enam nilai GCV diperoleh nilai GCV yang paling minimum adalah pada saat orde dua dengan satu titik knot. Sehingga pemilihan titik knot optimal terletak pada titik 39,6 dengan nilai GCV sebesar 0,03552. Plot titik knot dan nilai GCV secara kasar dapat dilihat pada Gambar 1.
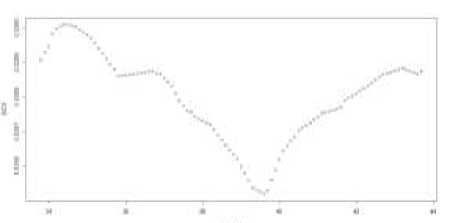
Gambar 1. Nilai GCV regresi semiparametrik spline truncated linear satu titik knot
Dari pemilihan titik knot optimal diperoleh estimasi model yang memiliki nilai GCV minimum yaitu pada saat orde 2 dengan satu titik knot yang terletak pada titik 39,6. Adapun estimasi model yang diperoleh adalah sebagai berikut:
̂I = -0,55021 - 0,01136НСТf+
0,01648(НСТi - 39,6)+ + 0,28815Si -0,04751Ui - 0,01104PLT i
dengan Yi adalah lama kesembuhan pasien DBD yang menjalani rawat inap di Rumah Sakit Puri Raharja Denpasar, tι adalah kadar hematokrit (HCT), Ki adalah suhu (S), K2 adalah umur (U), dan X3 adalah trombosit (PLT). Dengan nilai GCV sebesar 0,03552; MSE sebesar 0,02969; dan koefisien determinasi atau R2 = 0,98914, hal ini menunjukkan bahwa dengan memuat enam parameter variabel kadar hematokrit, suhu, umur, dan trombosit mampu menerangkan 98,914% keragaman lama kesembuhan pasien DBD yang menjalani rawat inap di Rumah Sakit Puri Raharja Denpasar. Sisanya 1,086% dipengaruhi oleh variabel lain di luar model ataupun error.
Pengujian parameter model dilakukan secara serentak (simultan) kemudian dilanjutkan dengan pengujian secara parsial (individu).
Tabel 3. Analisis Variansi Regresi Semiparametrik Spline Truncated Linear
|
Similar Kd.ιuaιιιaιι |
Dt |
JK |
H |
⅛t |
⅛rl fl = ι% |
|
Rearesi |
5 |
IJL¾M |
37.8729 |
1166.1« |
33177 |
|
Gsliit |
M |
2.0784 |
0.0325 | ||
|
Tcol |
W |
IDI 442⅛ |
Dari Tabel 3, diperoleh kesimpulan bahwa Khitung ≥ Ktabel yaitu 1166,186 ≥ 3,3177 maka tolak Hq yang mengindikasikan bahwa tidak semua koefisien regresi bernilai nol atau dengan kata lain terdapat pengaruh yang signifikan secara bersama-sama antara variabel bebas terhadap variabel terikat, sehingga model
signifikan. Selanjutnya dilakukan uji parameter secara parsial (secara individu) dengan uji t. Hasil pengujian tersebut disajikan dalam bentuk Tabel 4 berikut.
Tabel 4. Uji Individu Estimasi Model Regresi
Semiparametrik Spline Truncated Linear
|
ParEKtCT |
Eitunau |
Stdcv |
J-iliUU2 |
|
⅛ |
-0.5502L |
OJOtTl |
•1.79393 |
|
■0.01136 |
0.00205 |
•5.53007 | |
|
h |
0.01648 |
o≡r |
IJTll |
|
02S815 |
O-COtM |
3√0S48 | |
|
K2 |
-0.04751 |
OCWSS |
-5421042 |
|
•0.01104 |
O-OJjJ |
4S7JS |
Berdasarkan taraf nyata a = 1% dan nilai t - tabel = 2,654854 yang mengindikasikan tolak Hq . Dengan demikian dapat disimpulkan bahwa masing-masing parameter berpengaruh secara signifikan terhadap lama kesembuhan pasien.
Residual (goodness of fit) dari suatu model regresi harus memenuhi asumsi IIDN (0, σ2) yaitu identik, independen dan berdistribusi normal dengan mean nol dan variansi σ2 . Uji asumsi homogenitas dilakukan dengan menggunakan uji Glejser. Pada Tabel 5 diperoleh nilai ^hit sebesar 0,421 dan nilai signifikasinya sebesar 0,793 pada taraf nyata a = 1%, diperoleh bahwa nilai signifikansinya lebih besar dari 0,01. Maka dapat disimpulkan bahwa semua variabel tidak berpengaruh signifikan terhadap nilai mutlak residual. Hal tersebut membuktikan bahwa varians residual memenuhi asumsi homokedastisitas atau dengan kata lain tidak terjadi heteroskedastisitas.
Tabel 5. Analisis Variansi Uji Glejser
|
Snntber Keitistnun |
Db |
JX |
KT |
⅛r |
P - Htlw |
|
tai |
4 |
0-019 |
0-005 |
0.421 |
0.793 |
|
GilM |
65 |
0*24 |
0.011 | ||
|
Toial |
69 |
0*43 |
Selanjutnya dilakukan uji asumsi independen dengan menggunakan uji d Durbin-
Watson, diperoleh nilai d Durbin-Watson sebesar 1,579. Selanjutnya nilai d Durbin-Watson tersebut akan dibandingkan dengan nilai tabel signifikasi a = 1%, dengan jumlah sampel sebanyak 70 (T= 70), satu variabel dependen dan empat variabel independen (k= 5). Dari tabel d Durbin-Watson dengan a=1%, T= 70, dan k= 5 diperoleh nilai ^L dan ^U secara berturut-turut yaitu 1,34263 dan 1,57778 dengan:
4-dL =4-1,34263 = 2,65737 dan 4-du =4-1,57778 = 2,42222.
Karena nilai dari d Durbin-Watson terletak di antara nilai d-lj dan 4-du maka terima Hq yang mengin-dikasikan bahwa tidak terdapat autokorelasi positif ataupun negatif pada residual.
Tabel 6. Uji d Durbin-Watson

Sementara itu uji normalitas dilakukan dengan melakukan uji Anderson-Darling, diperoleh nilai Anderson-Darling sebesar 0,225 dan P - value sebesar 0,813 pada taraf nyata a = 1%. Karena P - value lebih besar dari 0,01, maka terima Hq yang mengindikasikan bahwa residual model memenuhi asumsi distribusi normal.
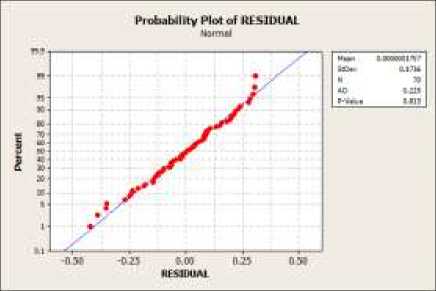
Gambar 3. Uji Anderson-Darling
Dengan demikian dapat disimpulkan bahwa residual dari model regresi semiparametrik spline truncated linear dengan satu titik knot
memenuhi asumsi IIDN (0, σ2) yaitu identik, independen dan berdistribusi normal.
-
4.7. Interpretasi Model Regresi
Semiparametrik Spline Truncated Linear dengan Satu Titik Knot
Model terbaik lama kesembuhan pasien DBD di Rumah Sakit Puri Raharja Denpasar menggunakan regresi semiparametrik spline truncated adalah model semiparametrik spline truncated linear (orde 2) dengan satu titik knot. Adapun interpretasi model regresi semi-parametrik spline truncated linear (orde 2) dengan satu titik knot adalah sebagai berikut. Dengan mengasumsikan suhu (S), umur (U), dan trombosit (PLT), konstan maka pengaruh kadar hematokrit (НСT), terhadap lama kesembuhan pasien (Y), apabila kadar
hematokrit naik sebesar 1% pada saat kadar hematokrit kurang dari 39,6%, maka Y akan mengalami penurunan sebesar 0,01136. Koefisien bernilai negatif artinya terjadi hubungan negatif antara kadar hematokrit dengan Y. Hal ini mengindikasikan bahwa apabila persentase kadar hematokrit menurun maka berakibat pada jenjang waktu yang lebih cepat pada kesembuhan pasien. Sedangkan ketika kadar hematokrit naik sebesar 1% pada saat kadar hematokrit lebih besar atau sama dengan 39,6% maka Y akan mengalami peningkatan sebesar 0,00512. Koefisien bernilai positif artinya terjadi hubungan positif antara kadar hematokrit dengan Y . Hal ini mengindikasikan bahwa apabila persentase kadar hematokrit meningkat maka berakibat pada jenjang waktu yang lebih lama pada kesembuhan pasien. Selanjutnya dengan mengasumsikan variabel yang lain konstan, maka interpretasi model berdasarkan masing-masing variabel (variabel suhu (S), umur (U), dan jumlah trombosit (PLT)) adalah sebagai berikut.
Apabila suhu (S) tubuh mengalami kenaikan 10C maka Y akan mengalami kenaikan sebesar 0,28815. Koefisien bernilai positif artinya terjadi hubungan positif antara suhu (S) dengan Y . Hal ini mengindikasikan bahwa ketika suhu
pasien meningkat menyebabkan kesembuhan pasien cenderung menjadi lebih lama.
Pada saat umur (U) mengalami kenaikan 1 tahun dan variabel bebas lainnya tetap, maka akan menurunkan Y sebesar 0,04751. Koefisien bernilai negatif artinya terjadi hubungan negatif antara umur dengan Y . Hal ini mengindikasikan bahwa semakin bertambahnya umur (U) pasien menyebabkan kesembuhan pasien cenderung menjadi lebih cepat.
Sedangkan ketika jumlah trombosit (PLT) menglami kenaikan 1(× 103/μL), dan variabel bebas lainnya tetap, maka akan menurunkan Y sebesar 0,01104. Koefisien bernilai negatif artinya terjadi hubungan negatif antara PLT dengan Y . Hal ini mengindikasikan bahwa semakin meningkat jumlah trombosit pasien, menyebabkan kesembuhannya pasien cenderung semakin cepat.
-
4.8. Hasil Regresi Semiparametrik Spline
Truncated Linear dengan Estimasi Fungsi Regresi Semiparametrik dan Estimator Kernel Uniform
Berdasarkan penelitian sebelumnya yang dilakukan oleh Fitriani (2015), variabel umur, suhu tubuh, dan trombosit diasumsikan sebagai komponen parametrik dan variabel kadar hematokrit diasumsikan sebagai komponen nonparametrik sedangkan lama demam dan nadi diasumsikan tidak berpengaruh signifikan terhadap lama kesembuhan pasien yang sudah diwakili oleh variabel bebas lain yang signifikan.
Penduga fungsi regresi semiparametrik dengan estimator kernel uniform ( ̂i), yang dilakukan oleh Fitriani (2015) diperoleh model regresi semiparametrik sebagai berikut:
̂ i = – 0,005496 + 0,265939 S – 0,472707 U –
0,330655 PLT + ̂■h (ti)
dengan bandwidth optimal sebesar 0,005, nilai GCV minimum sebesar 5,329214e-09, nilai MSE minimum sebesar 0,00437 dan dengan nilai koefisien determinasi atau R2 sebesar 98,90%.
Sedangkan pada regresi semiparametrik spline truncated linear diperoleh model sebagai
berikut:
̂j = -0,55021 - 0,01136НСTj+
0,01648(НСT j - 39,6)+ + 0,28815Si -
0,04751Ui - 0,01104PLT
dengan nilai GCV minimum sebesar 0,03552, nilai MSE sebesar 0,02969, nilai koefisien determinasi atau R2 sebesar 98,91% yang terletak pada titik 39,6 dan dengan enam parameter.
Variabel yang signifikan berpengaruh terhadap model regresi semiparametrik spline truncated linear (orde 2) dengan satu titik knot yaitu umur (tahun), suhu tubuh (℃), trombosit (×103/μL), dan kadar hematokrit (%). Nilai GCV minimum sebesar 0,03552045, nilai MSE sebesar 0,0296922, nilai R2sebesar 98,91% dicapai pada titik knot 39,6.
Dalam penelitian ini dibahas model regresi semiparametrik untuk satu variabel pada komponen nonparametriknya sehingga penelitian lebih lanjut dapat dilakukan untuk lebih dari satu variabel komponen nonparametrik.
DAFTAR PUSTAKA
Anderson, T. W., and D. A. Darling. 1954. "A Test of Goodness of Fit." Journal of the American Statistical Association 49 (268): 765-769.
Departemen Kesehatan Republik Indonesia . 2004. Tata Laksana Demam Berdarah Dengue di Indonesia. Ketiga. Jakarta: Departemen Kesehatan.
Eubank, R. L. 1988. Spline Smoothing and Nonparametric Regression. New York:
Marcel Dekker. inc.
Fitriani, A. 2015. "Estimasi Model Regresi Semiparametrik Menggunakan Esti-mator Kernel Uniform (Studi Kasus: Pasien DBD di RS Puri Raharja)." Skripsi. Jurusan Matematika Universitas Udayana.
Gujarati, D. N. 2006. Essential of Econometrics.
Translated by Julius A. Mulyadi and Yelvi Andri. United States Military Academy, West Poit: McGraw-Hill Companies.
Kutner, M. H., C. J. Nachtsheim, J. Neter, and
W. Li. 2004. Applied Linear Statistical Model. 4. New York: McGraw-Hill/Irwin.
Laome, L. 2009. "Model Regresi Semiparametrik Spline Untuk Data Longitudinal pada Kasus Kadar CD4 Penderita HIV." Paradigma 13 (2): 101-106.
Lyche, T., and K. Morken. 2008. Spline Methods Draft. Norwegia: Department of Informatics Centre of Mathematics for Applications University of Oslo.
Marina, S.M. T., and I N. Budiantara. 2013. "Pemodelan Faktor-Faktor yang Mempengaruhi Persentase Kriminalitas di Jawa Timur dengan Pendekatan Regresi Semiparametrik Spline." Jurnal Sains dan Seni POMITS 2 (2): D-147 - D-152.
Neter, J., W. Wasserman, and M. H. Kutner. 1990. Applied Linear Statistical Models. Third. Translated by Bambang Sumantri. New York: McGraw-Hill College.
Ruppert, D., M. P. Wand, and R. J. Carroll. 2003. Semiparametric Regression. New York: Cambridge University Press.
Sugiantari, A. P., and I N. Budiantara. 2013. "Analisis Faktor-Faktor yang Mempengaruhi Angka Harapan Hidup di Jawa Timur Menggunakan Regresi Semi-parametrik Spline." Jurnal Sains dan Seni POMITS 2 (1): D-37 - D-41.
Wibowo, W., S. Haryatmi, and I N Budiantara. 2013. "Kajian Metode Estimasi Para-meter dalam Regresi Semi-parametrik Spline." Berkala MIPA 23 (1): 102-110.
73
Discussion and feedback