PERBANDINGAN METODE MCD-BOOTSTRAP DAN LAD-BOOTSTRAP DALAM MENGATASI PENGARUH PENCILAN PADA ANALISIS REGRESI LINEAR BERGANDA
on
E-Jurnal Matematika Vol. 6 (1), Januari 2017, pp. 47-55
ISSN: 2303-1751
PERBANDINGAN METODE MCD-BOOTSTRAP DAN LAD-BOOTSTRAP DALAM MENGATASI PENGARUH PENCILAN PADA ANALISIS REGRESI LINEAR BERGANDA
Ni Luh Putu Ratna Kumalasari1§, Ni Luh Putu Suciptawati2§,,
Made Susilawati3
1Jurusan Matematika, FMIPA – Universitas Udayana [Email: ratnakumalasari22@gmail.com]
2Jurusan Matematika, FMIPA – Universitas Udayana [Email: putusuciptawati@yahoo.co.id]
3Jurusan Matematika, FMIPA – Universitas Udayana [Email: susilawati.made@gmail.com] §Corresponding Author
ABSTRACT
Outliers are observations that are far away from other observations. Outlier can be interfered with the process of data analysis which influence the regression parameters estimation. Methods that are able to deal with outliers are Minimum Covariance Determinant and Least Absolute Deviation methods. However, if both methods are applied with small sample the validity of both methods is being questioned. This research applies bootstrap to MCD and LAD methods to small sample. Resampling using 500, 750,and 1000 with confidence interval of 95% and 99% shows that both methods produce an unbiased estimators at 10%, 15%, and 20% outliers. The confidence interval of MCD-Bootstrap method is shorter than LAD-Bootstrap method. Both are, MCD-Bootstrap method is a better thus than LAD-Bootstrap method.
Keywords: Bootstrap, Least Absolute Deviation (LAD), Minimum Covariance Determinant (MCD), Outliers.
Analisis regresi merupakan metode statistika yang bertujuan untuk menganalisis hubungan atau pengaruh antara satu atau lebih peubah prediktor terhadap peubah respons. Analisis regresi linear dibagi menjadi dua jenis yaitu analisis regresi linear sederhana dan analisis regresi linear berganda. Analisis regresi linear berganda adalah analisis regresi yang melibatkan dua atau lebih peubah prediktor dengan satu peubah respons. Model regresi linear berganda dapat dituliskan sebagai berikut:
Yi = 0+ 11^1 1 +-----+ βk%ik + εi (1)
Pada analisis regresi, metode estimasi yang digunakan untuk menduga parameter serta memiliki sifat tidak bias adalah Metode Kuadrat Terkecil (MKT) atau Ordinary Least of Square (OLS). Penggunaan MKT memerlukan asumsi-asumsi tertentu yang harus dipenuhi antara lain adalah galat (sisaan) harus memenuhi asumsi kenormalan. Namun dalam berbagai kasus
penelitian, tidak jarang ditemukan pelanggaran terhadap asumsi kenormalan. Salah satu penyebabnya adalah adanya pencilan (outlier) pada data amatan.
Pencilan merupakan data amatan yang menyimpang jauh lebih besar atau jauh lebih kecil dari data amatan lainnya. Oleh karena itu, diperlukan alternatif dalam pemilihan metode estimasi yang tepat tanpa menghilangkan data pencilan. Metode yang mampu menghasilkan penduga parameter yang robust atau kekar terhadap adanya pencilan pada analisis regresi linear berganda adalah Minimum Covariance Determinant (MCD) dan Least Absolute Deviation (LAD). Akan tetapi, jika kedua metode ini dihadapkan pada data yang berjumlah sedikit maka diragukan. Oleh sebab itu, perlu dilakukannya penelitian terhadap pengaplikasian bootstrap atau resampling pada metode MCD dan metode LAD dengan data yang berjumlah sedikit.
Prinsip bootstrap adalah menduga parameter untuk masing-masing jumlah sampel yang
diperoleh dengan mengambil sampel berukuran n dari nilai-nilai data asli. Sampel tersebut merupakan sampel acak dengan pengembalian, artinya bahwa beberapa nilai sampel asli akan berulang dan beberapa diantaranya tidak akan terambil sama sekali (Sprent, 1989). Metode bootstrap yang digunakan pada regresi linear adalah bootstrap residual. Metode bootstrap residual adalah metode yang meresampling sisaannya.
Berdasarkan pemaparan di atas, penulis tertarik melakukan perbandingan terhadap metode MCD-Bootstrap dan LAD-Bootstrap dalam mengatasi pengaruh pencilan pada analisis regresi linear berganda. Hal ini dapat ditunjukkan dengan membandingkan bias penduga parameter dan lebar selang yang dihasilkan oleh metode MCD-Bootstrap dan LAD-Bootstrap.
Dengan demikian, tujuan dari penelitian ini adalah untuk mengetahui bias yang dihasilkan oleh metode MCD-Bootstrap dan LAD-Bootstrap.
Metode Kuadrat Terkecil (MKT)
Metode kuadrat terkecil adalah salah satu metode yang sering digunakan untuk menduga parameter dalam analisis regresi linear berganda. MKT meminimumkan jumlah kuadrat sisaan (galat), sehingga nilai parameternya mendekati nilai sesungguhnya. Menurut Teorema Gauss-Markov, setiap pendugaan MKT yang asumsinya terpenuhi akan bersifat BLUE (Best Linear Unbiased Estimator).
Pencilan (Outlier)
Pencilan merupakan data amatan yang berada jauh dari amatan lainnya. Pencilan dalam data akan mengganggu proses analisis data sehingga dapat memberikan pengaruh yang besar terhadap pendugaan parameter regresi. Keberadaan pencilan akan menimbulkan suatu masalah dalam metode kuadrat terkecil (Neter, et al., 1997).
Minimum Covariance Determinant (MCD)
MCD merupakan metode penduga parameter dengan meminimumkan determinan matriks kovarians. Prinsip MCD adalah dengan menggunakan vektor rata-rata dan matriks kovarians yang didapat dari penduga MCD untuk menentukan bobot dari setiap data, sehingga akan didapat penduga parameter model MCD. Metode ini bertujuan untuk mencari subsampel H yang berukuran ℎ dari keseluruhan n amatan dengan ℎ ≤ n yang matriks kovariansnya memiliki determinan terkecil di antara semua kombinasi kemungkinan data (Hubert & Debruyune, 2009).
Adapun nilai ℎ dapat ditentukan dengan rumus sebagai berikut:
ℎ= 2 (2) Untuk nilai vektor rataan V MCD dan matriks kovarians ^MCD diberikan:
$mcd = ∑ieH [Xi - Vmcd ] [ Xi - Vmcd ]t (4)
Dari persamaan (3) dapat diketahui nilai determinan matriks kovarians. Jika det(Smcd)≠ 0, maka kemudian hitung jarak Mahalanobis. Menghitung jarak Mahalanobis yang kekar diperoleh dengan rumus:
RD (xi) =√(Xi - Vmcd ) tSmcd (Xi - Vmcd) (5)
Adapun langkah-langkah penduga MCD dengan Fast-MCD adalah mengambil himpunan bagian dari matriks X secara acak, misalkan himpunan bagian tersebut Hy dengan jumlah elemen sebanyak ℎ. Hitung vektor rataan Vmcd dan matriks kovarians Smcd pada Hy dengan persamaan (3) dan (4).
Misalkan Vmcd = dan Smcd = , serta hitung det(1^l ). Apabila det(1^l ) = 0 maka berhenti, tetapi jika det(1^l ) ≠ 0, maka hitung Robust Distance (RD) menggunakan persamaan (5). Nilai RD yang diperoleh akan diurutkan dari nilai terkecil. Demikian seterusnya hingga mencapai det(Si+\ ) = det(Sy ). Ulangi langkah diatas dengan mengambil himpunan H selanjutnya. Pilih himpunan H yang memiliki nilai determinan matriks kovarians terkecil, selanjutnya mencari nilai Vmcd dan Smcd .
Berdasarkan anggota ℎ tersebut, selanjutnya data diboboti:
1,jika ( xi - ^MCD ) 7^MCD (Xi - Vmcd)≤Xp ;1-a
0, lainnya
Pembobot Wi dapat membentuk matriks WMCD berukuran n×n, sebagai berikut:
Wl2
W22
Wn2
^MCD
[ W2I
⋮
Wi 3 …
W23 …
Wn3 …
Sehingga diperoleh penduga MCD dengan
persamaan:
̂ MCD=(XtWmcdX) (XtWmcdY) (6)
Least Absolute Deviation (LAD)
Least Absolute Deviation (LAD) merupakan metode penduga parameter untuk menangani masalah galat yang tidak berdistribusi normal. Metode LAD dikenal dengan berbagai istilah yaitu Minimum Absolute Deviation dan Least Absolute Value (LAV). Penaksiran LAD untuk mendapakan β adalah meminimumkan jumlah nilai mutlak dari galat yaitu:
̂ = min ∑ !U | ^i |
= min ∑ F=i | Yi - XiPlad | (7)
Metode penaksiran LAD dapat dimodelkan sebagai berikut:
̂=(XtWladX) -1 (XT Wlad) (8)
dengan W adalah matriks diagonal dengan elemen diagonalnya wH .
Wii = {
i I , jika | £i |≠0 1, jika | εi|=0
dengan εi adalah galat dari nilai awal yang telah diperoleh dari metode kuadrat terkecil (El-Salam, 2013).
Bootstrap Residual
Metode bootstrap akan menghasilkan dugaan koefisien regresi ( ̂ ∗) sebanyak jumlah ulangan (B). Langkah-langkah bootstrap residual adalah menentukan nilai ̂ dari model analisis regresi yang telah ditetapkan. Selanjutnya menghitung nilai residual yaitu
e= - ̂, diperoleh e ={eι , e2,…,en}. Mengambil sampel bootstrap berukuran n dari eι , e2,…,en secara acak dengan pengembalian, diperoleh sampel bootstrap e∗={eι ∗, C2 ,…,en∗}. Menghitung nilai bootstrap untuk Y ∗ dengan menambahkan e ∗, sehingga menghasilkan ̂ ∗. Mengulagi proses diatas ssuai dengan ulangan (B) yang diinginkan (Sungkono, 2013).
Data yang digunakan dalam penelitian ini adalah data simulasi yang diperoleh dengan membangkitkan data berdistribusi normal. Data dibangkitkan dengan bantuan program R i386 3.2.0. Data yang dibangkitkan dimodelkan dalam regresi linear berganda. Banyaknya sampel yang digunakan adalah 40 amatan. Persentase pencilan yang akan digunakan yaitu 10%, 15%, dan 20%.
Langkah pertama dari penelitian ini adalah membangkitkan nilai sisaan (e ) yang berdistribusi normal sebanyak 40 dengan rataan 0 dan varians 1. Selanjutnya, membangkitkan peubah prediktor sebanyak 40 amatan Xi ~N(60,5) dan ^2 ~ TV(80,3). Menentukan nilai peubah respons dengan nilai parameter yang telah ditentukan yakni βo =3, dan βl , β2 =1. Pencilan dibangkitkan pada peubah respons sebesar 10%, 15%, dan 20%. Kemudian, menghitung nilai peubah respons yang telah ditambahkan pencilan. Langkah berikutnya, dilakukan uji Anderson-Darling untuk melihat kenormalan data, pendeteksian pencilan dengan plot robust distance dan dianalisis dengan menggunakan Metode Kuadrat Terkecil (MKT).
Langkah selanjutnya, data dianalisis dengan metode MCD-Bootstrap yaitu menduga nilai parameter dengan mencari nilai vektor rataan dan matriks kovarians MCD. Selanjutnya untuk menemukan βo , βγ ,dan β2 , sisaan yang diperoleh dari metode MCD kemudian diresampling dengan metode bootstrap residual sebanyak 500, 750, dan 1000 kali ulangan dengan selang kepercayaan 95% dan 99%. Selanjutnya, dilakukan analisis dengan metode
LAD-Bootstrap. Dilakukan resampling pada sisaan yang diperoleh dari metode LAD-Bootstrap. Resampling dilakukan
sebanyak 500, 750, dan 1000 kali dengan selang kepecayaan 95% dan 99%. Langkah terakhir, yakni membandingkan hasil yang diperoleh dari kedua metode tersebut.
Pemeriksaan kenormalan data menggunakan uji kenormalan Anderson-Darling dilakukan dengan menggunakan program Minitab 17. Hipotesis sebagai berikut:
Hq : sisaan menyebar secara normal
H^ : sisaan tidak menyebar secara normal
Sisaan dikatakan menyebar secara normal (terima Hq) apabila nilai p-value lebih besar dari alfa (a). Demikian sebaliknya, sisaan dikatakan tidak menyebar secara normal (tolak Hq ) apabila nilai p-value lebih kecil dari alfa (a). Pada penelitian uji kenormalan data ini, alfa (a) yang digunakan sebesar 0,05. Nilai p-value pada uji Anderson-darling disajikan pada table berikut:
Tabel 1. Uji Kenormalan Data
|
Persentase Pencilan |
P-value |
Keterangan |
|
Data awal (tanpa pencilan) |
0,551 |
Terima Hq (normal) |
|
10% |
< 0,005 |
Tolak Ho (tidak normal) |
|
15% |
< 0,005 |
Tolak Ho (tidak normal) |
|
20% |
< 0,005 |
Tolak H0 (tidak normal) |
Berdasarkan hasil uji kenormalan data dengan uji Anderson-Darling, dapat dilihat bahwa data awal (tanpa pencilan) memiliki nilai p-value yang lebih besar dari alfa (a) sebesar 0,05. Hal ini berarti data awal (tanpa pencilan) merupakan data yang menyebar secara normal. Namun nilai p-value pada data yang memiliki persentase pencilan sebesar 10%, 15%, dan 20% menunjukkan bahwa data yang mengandung pencilan merupakan data tidak menyebar secara normal.
menggunakan Robust Distance (RD) dengan bantuan program Ri386 3.2.0. Pencilan dapat diklasifikasikan dengan plot outlier yang berguna untuk membedakan data amatan. Plot yang dihasilkan akan membagi amatan atas 4 kuadran berdasarkan jenis pencilan yang terdeteksi. Pada pemeriksaan pencilan dengan Robust Distance diperoleh plot sebagai berikut:
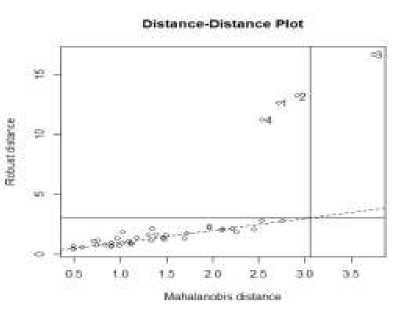
Gambar 1. Plot RD pada Pencilan 10%
Amatan yang terdeteksi pencilan antara lain adalah amatan ke-1, 2, 3 dan 4. Terlihat bahwa terdapat sebanyak 1 amatan yang berada pada kuadran I yang merupakan bad laverage dan terdapat sebanyak 3 amatan yang berada pada kuadran II yang merupakan outlier orthogonal. Berikutnya pencilan dengan persentase 15%.
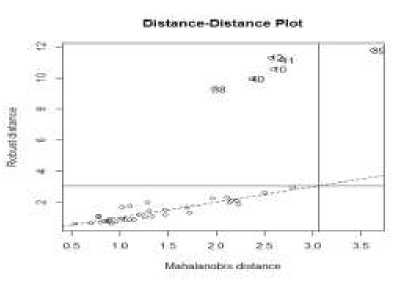
Gambar 2. Plot RD pada Pencilan 15%
Amatan yg terdeteksi pencilan adalah amatan ke-10, 11, 12, 38, 39 dan 40. Pada kuadran I terdapat 1 amatan dan pada kuadran II terdapat 5 amatan. Hal ini berarti 1 amatan termasuk bad laverage yaitu amatan ke-39 dan 5 amatan termasuk outlier orthogonal. Selanjutnya plot RD dengan pencilan 20% :
DFfttance-DistAnce Plot

0 5 10 15 20 2 5 10 3.5 4 0
Mλh∣iM∣⅛<>∣i <>⅞uncM
Gambar 3. Plot RD pada Pencilan 20%
Pada Gambar 3 terlihat pada pencilan 20% terdapat 8 amatan yang terdeteksi pencilan. Amatan tersebut adalah amatan ke-1, 2, 15, 16, 20, 22, 35 dan 36. Amatan jenis pencilan bad leverage sebanyak 1 amatan yang berada pada kuadran I. Sedangkan pada kuadran II terdapat sebanyak 7 amatan yang termasuk outlier orthogonal.
Metode awal yang digunakan untuk menduga nilai parameter pada penelitian ini adalah MKT. Data awal tanpa pencilan dan data dengan pencilan, selanjutnya akan dianalisis dengan menggunakan MKT. Selang kepercayaan yang digunakan adalah 95% dan 99%. Diperoleh nilai parameter dengan MKT, sebagai berikut:
Tabel 2. Analisis dengan MKT
|
PasciasePecihii |
Pnaneer |
EstIIIlHl |
Sdag ⅛κay≡ |
Keterangan |
|
Dataawii IaiipapfQGlin. |
A |
28,88'9$ |
1028113-395:210 |
IidckBiis |
|
0J5I86 |
0,82283-1,K088 |
TidakBiis | ||
|
A |
0,83413 |
(157599-1,09226 |
TidakBjis | |
|
10% |
A |
⅛532I1 |
114321'43,198“ |
Tidak Bjis |
|
A |
1,47372 |
0,62D26-L4140 |
Bias | |
|
A |
≡ |
OJlS Γ4,92539 |
Bias | |
|
15% |
A |
52^3148 |
W⅛⅛0978l |
Bias |
|
13934' |
0,58459-129198 |
Bias | ||
|
125263 |
0,44370-1,13315 |
Bias | ||
|
29% |
5626652 |
20,86231-5228622 |
Bias | |
|
01 |
1.49318 |
0,73625-120425 |
Bias | |
|
138419 |
055607-1,15338 |
Bias |
Tabel 3. Analisis dengan MKT
|
Perscrase Pcaian |
Paramero |
EsuniiSi |
Sehng Kepercayaan |
Keterangan |
|
Dataawal Ianpa pαu⅛α |
A |
28,88'98 |
16,944134258210 |
Tidakffias |
|
A |
0,95186 |
0,77894-1,1247* |
Tidak Bias | |
|
A |
0,83413 |
0,48818-1,18007 |
Tidak Bias | |
|
19*» |
A |
40,53211 |
14,6721549,01827 |
TidakBias |
|
A |
1,4732 |
0,60905-1,4224l |
Bias | |
|
A |
120976 |
0,51058-1,15708 |
Bias | |
|
15% |
A |
5193149 |
29,1264148.67122 |
Bias |
|
A |
13934' |
0,71209-123925 |
Bias | |
|
A |
125263 |
0,87063-1,00648 |
Bias | |
|
20% |
⅛ |
5656652 |
20.89'61-50.97762 |
Bias |
|
A |
1.49318 |
0,78471-1,37269 |
Bias | |
|
A |
138419 |
0.64305-120583 |
Bias |
Berdasarkan Tabel 2 dan Tabel 3 diperoleh bahwa data awal tanpa pencilan untuk selang kepercayaan 95% dan 99% adalah tidak bias. Hal ini dapat disimpulkan karena nilai penduga parameter ^O , ^l dan ^2 yang dihasilkan oleh analisis metode MKT berada antara lebar selang kepercayaan yang sudah diberikan. Hasil yang sama diperlihatkan saat persentase pencilan 10% untuk parameter ^O yang bersifat tidak bias. Namun untuk parameter βl dan β2 pada persentase 10% tidak berada pada selang kepercayaan 95% dan 99%.
Dilain pihak, nilai penduga parameter pada data dengan persentase pencilan sebesar 15% dan 20% untuk selang kepercayaan 95% dan 99% tidak berada pada lebar selang yang sudah diberikan. Hal ini berarti, penduga parameter βo , βl , dan β2 yang dihasilkan mengalami bias. Karena data dengan pencilan mengalami bias pada analisis MKT, maka akan dilanjutkan menganalisis dengan metode MCD-Bootstrap dan LAD-Bootstrap.
-
4.4 Analisis Data dengan Metode Minimum Covariance Determinant (MCD-Bootstrap
Langkah pertama dari analisis MCD adalah menduga parameter regresi dengan mencari nilai vektor rataan dan matriks kovarians MCD. Selanjutnya untuk menemukan βo , βx , dan β2 pada data yang mengandung pencilan sebesar 10%, 15% , dan 20%, sisaan yang diperoleh dari metode MCD kemudian diresampling dengan metode bootstrap residual.
Resampling dilakukan sebayak 500, 750, dan 1000 kali ulangan. Selang kepercayaan yang digunakan adalah selang kepercayaan sebesar 95% dan 99%.
Tabel 4. Analisis Metode MCD-Bootstrap dengan B = 500, SK= 95%
|
Ptnata pacta |
Parjintter |
Estuiusi |
Selanit Kepetayaaa 95% |
Krtearspn | |
|
Batas Bawah |
Batas Atas | ||||
|
10* |
ft |
27.36254 |
14,58490 |
39,77970 |
Liiiakbias |
|
ft |
1.01700 |
0,93227 |
1,19616 |
Tidakbias | |
|
ft |
0,68452 |
O.5J5S5 |
0,94587 |
Tidakbias | |
|
IM |
ft |
27,40943 |
12.4216» |
41.94291 |
Tidakbias |
|
f: |
1,01269 |
0,72193 |
1,10650 |
Tidakbias | |
|
ft |
0,68735 |
0.50882 |
0,97289 |
Tidakbias | |
|
ft |
27,19416 |
12.66719 |
41.69741 |
Tidakbias | |
|
f: |
1,01218 |
0.92321 |
1.10522 |
Tiiikjrj | |
|
0.6910* |
0.51*80 |
0,96391 |
Tidakbias | ||
Tabel 5. Analisis Metode MCD-Bootstrap dengan B = 500, SK= 99%
|
Pasanase pβκilan |
PasanieiH |
Esiinuii |
Selang Ktptreayaan 99*⅛ |
KelHiigli! | |
|
Batas Bawah |
Batas Alai | ||||
|
10*∣ |
ft |
27.21720 |
10,78117 |
43.58343 |
Tuiikbias |
|
ft |
1,01755 |
0,90371 |
1.2247’ |
Tuiak bias | |
|
ft |
0,68592 |
0.49269 |
Q.889O3 |
Tubkbias | |
|
15S |
ft |
27.05674 |
9,5355’ |
45,8290’ |
Ttdakbias |
|
ft |
1.01676 |
0.88’28 |
1,1451* |
Tiibkbias | |
|
ft |
0,68878 |
0.43932 |
1.04239 |
Tubkbias | |
|
20% |
ft |
26,85559 |
11,52642 |
46.83818 |
Tubkbias |
|
ft |
1.014)0 |
0,89732 |
1,13110 |
Tubkbias | |
|
0,89375 |
0.45006 |
0,93165 |
Tiibkbias | ||
Tabel 6. Analisis Metode MCD-Bootstrap dengan B = 750, SK= 95%
|
Perseiirzse penoiaa |
PaiaDetH |
Estinias- |
Selang Kepetcayaan 95% |
Keteransan | |
|
BataBawah |
Batas Atas | ||||
|
IWi |
ft |
27.10400 |
14.56568 |
39.79892 |
Tidakbias |
|
ft |
1.11461 |
0,93351 |
139491 |
Tidaktras | |
|
ft |
0.58961 |
0,53588 |
0,84584 |
Tidaktsas | |
|
15% |
ft |
26.92436 |
11,20819 |
43.15641 |
Tidaktras |
|
ft |
1,01307 |
0,9173« |
1.11106 |
Tidaktras | |
|
ft |
0.89313 |
0,50129 |
0.98043 |
Tidaktras | |
|
20% |
ft |
26.83828 |
12,265'2 |
42,09888 |
Tidaktas |
|
ft |
1.117*8 |
0,91530 |
1.21313 |
Tidaktsas | |
|
ft |
0.99128 |
0,50995 |
1,07176 |
Tidaktias | |
Tabel 7. Analisis Metode MCD-Bootstrap dengan B = 750, SK= 99%
|
Penentase JiKitilnn |
Parameter |
Estimasi |
Selin? Kepercsysio 99% |
Kelersegan | |
|
Batai Bswah |
BslM Atas | ||||
|
10% |
ft |
2’08484 |
9.69528 |
44.66932 |
Tubkbta |
|
ft |
0j91526 |
0.91279 |
1,21563 |
Tubkbta | |
|
ft |
0,577,s∣ |
0.47826 |
0,90346 |
Titbkbta | |
|
15% |
ft |
27243’2 |
10.47284 |
44.8917« |
Ttdakbias |
|
ft |
1.01512 |
O.7B724 |
1,141IB |
Tidakbta | |
|
ft |
0.78758 |
0.4391» |
0.94232 |
Tuikbias | |
|
20% |
ft |
27.17589 |
8224IO |
46,14050 |
Itibkbta |
|
ft |
1.01446 |
0.89477 |
1.23365 |
Tiiikbias | |
|
0.68948 |
0.46398 |
0,91773 |
Tidskbias | ||
Tabel 8. Analisis Metode MCD-Bootstrap dengan B = 1000, SK= 95%
|
Pfrsetiiase pen⅛aιι |
ParaisetH |
Estimasi |
Seiang Keperayaan 95⅛ |
Kelerargan | |
|
Batas Biwah |
BatasAtas | ||||
|
10% |
ft |
26 '33’6 |
14,01490 |
4034970 |
Tidakbias |
|
ft |
1.01624 |
0,83014 |
1.19829 |
Ttdakbias | |
|
ft |
0.79298 |
0.53081 |
0,85090 |
Tidakbta | |
|
15% |
ft |
27,02557 |
11,58506 |
42.77954 |
Jidakbias |
|
ft |
1.01295 |
0,81412 |
1.11430 |
Tidakbias | |
|
ft |
0.59194 |
0.49840 |
1.0833’ |
Tidakbta | |
|
20% |
ft |
27,49510 |
1228192 |
42.08268 |
Ttdakbias |
|
ft |
1,01303 |
0,92174 |
1.12668 |
Tidakbias | |
|
ft |
0.68654 |
0.50903 |
0.8’268 |
Tidakbias | |
Tabel 9. Analisis Metode MCD-Bootstrap dengan B = 1000, SK= 99%
|
Persentase pencils |
Parameter |
Estunasi |
Selang Krprraywc 99% |
Keterangan | |
|
Batas Bawali |
Batas Atas | ||||
|
10% |
ft |
26.9’03* |
9,’6541 |
44.59919 |
Tidakbias |
|
ft |
0-91582 |
0,80968 |
I,U 8'4 |
Tklakbias | |
|
ft |
0.69038 |
0.4*906 |
0.90266 |
Tklakbas | |
|
; |
ft |
27.02121 |
6,35*50 |
48,00’10 |
Tidak bias |
|
ft |
l.01370 |
0,88’90 |
1,14552 |
Tidakbias | |
|
P: |
0.69139 |
0.43357 |
0.94814 |
Tidakbus | |
|
20% |
ft |
27.10866 |
7,88’06 |
46.4”53 |
Tidakbias |
|
ft |
I.Ol 241 |
0.89734 |
1,33108 |
Tidakbtas | |
|
0.89192 |
0,45456 |
0,92715 |
Tidakbtas | ||
Sifat tidak bias pada selang kepercayaan 95% dan 99% terjadi apabila nilai parameter regresi yaitu βo , βl , dan β2 berada pada selang kepercayaan yang sudah diberikan. Pada Tabel 4, 5, 6, 7, 8 , dan 9 dapat dilihat bahwa nilai parameter dari data dengan pencilan
sebesar 10%, 15%, dan 20% berada pada selang kepercayaan. Hal ini berarti data bersifat tidak bias pada selang kepercayaan 95%, 99% dengan resampling 500, 750, dan 1000 kali ulangan.
-
4.5 Analisis Data dengan Metode Least
Absolute Deviation (LAD)-Bootstrap
Langkah berikutnya yang dilakukan setelah data pencilan dianalisis dengan menggunakan metode MCD-Bootrtrap adalah menganalisis data pencilan dengan metode LAD-Bootstrap. Untuk menduga nilai parameter regresi, data yang mengandung pencilan sebesar 10%, 15%, dan 20% akan dianalisis dengan metode LAD.
Selanjutnya dilakukan resampling sebanyak 500, 750, dan 1000 kali ulangan bootstrap residual. Berikut hasil analisis dengan metode LAD-Bootstrap.
Tabel 10. Analisis Metode LAD-Bootstrap dengan B=500 , SK= 95%
|
Perseπ!ιse Pmrilan |
Paramtlo |
Eshmast |
Selang Kepatayann 95% |
KdGftngsn | |
|
Bafas Basrah |
Bafas Atas | ||||
|
ιo⅜ |
ft |
40,0’568 |
35363’6 |
63.4087- |
Tι∂ιk bias |
|
P' |
1J2953 |
0,7355’ |
1,34’15 |
TiOikbias | |
|
P1 |
0.82608 |
0.64511 |
IJMTl |
Tidik bias | |
|
i SH |
ft |
42X72’8 |
27,95160 |
60.99660 |
Tidik bias |
|
ft |
1X5421 |
0.53560 |
1,44712 |
Tidikbias | |
|
ft |
0.40082 |
1.04973 |
Tidik bias | ||
|
20H |
ft |
⅛√⅛⅛ |
'■ ■:■;.’' |
<li,..,l,1 |
Tidik bias |
|
ft |
1,25642 |
WUW |
1,5'078 |
Tidikbias | |
|
O,«0'6 |
0.46264 |
1.01156 |
TuOikbias | ||
Tabel 11. Analisis Metode LAD-Bootstrap dengan B=500 , SK= 99%
|
Persentae penaan |
Pansaetet |
Estimasi |
Seltns Kepetayaan 99*» |
KeteranBiii | |
|
Batas Bawah |
Batas Atas | ||||
|
MK |
ft |
40J7057 |
23,184’- |
60,22938 |
Tidak bias |
|
ft |
1.23771 |
0,6696] |
1,31311 |
Tidak bias | |
|
ft |
1237’1 |
0,37132 |
1,02023 |
Tidakbias | |
|
15% |
ft |
4432462 |
34,032'9 |
-∣.0"'9 |
Tidak bias |
|
ft |
U572i |
0,43557 |
1,44715 |
Tidak bias | |
|
ft |
0.50838 |
0,23IOO |
0,97991 |
Tidak bias | |
|
MK |
ft |
41.26789 |
26,81105 |
63.85606 |
Tidak bias |
|
ft |
1.05865 |
0,59634 |
1.48638 |
Txiak bias | |
|
ft |
0.85175 |
0,46003 |
1,00895 |
Tidak bias | |
Tabel 12. Analisis Metode LAD-Bootstrap dengan B=750 , SK= 95%
|
Petseniase (Mieilan |
Pirarsetet |
Esiiitasi |
Selan; Kepereayaan 95% |
Keleraagm | |
|
Balas Banih |
EtoB Atas | ||||
|
10% |
ft |
4X43778 |
28,97’93 |
56,02294 |
Tidakbiai |
|
ft |
1,25330 |
0.56247 |
1,22025 |
Tidakbias | |
|
ft |
0.51643 |
032821 |
O.9"∣3 |
Tiildkbias | |
|
15% |
ft |
43.02655 |
3024352 |
67.28852 |
Tidakbias |
|
ft |
1.1494’ |
0.64’04 |
1,33568 |
TiiLikbias | |
|
ft |
0.82991 |
0.62262 |
1,17153 |
Tidakbias | |
|
20% |
ft |
44,76784 |
1’86’32 |
64,91232 |
Tidakbias |
|
ft |
1,12560 |
0.73958 |
1.44314 |
Tidakbias | |
|
ft |
0.69551 |
0.55432 |
I :“S: |
Tidakbias | |
Tabel 13. Analisis Metode LAD-Bootstrap dengan B=750 , SK= 99%
|
Pasentase Penrilan |
PnrimftG |
Estnrasi |
Selang Kepermyam 99% |
Krcrangin | |
|
Bans Bawah |
Batas Atas | ||||
|
10% |
ft |
41,40104 |
26,33’62 |
61.38063 |
Tidak bias |
|
ft |
1,23694 |
0,46899 |
1.41373 |
Tidak bias | |
|
ft |
0,95’” |
0.48598 |
1,13489 |
Tidak bias | |
|
15% |
ft |
40,08556 |
24.2002 2 |
61.24522 |
Tidak bias |
|
ft |
1,03437 |
0,42-503 |
1.05769 |
Tidak bias | |
|
ft |
0,7’472 |
0,38757 |
093648 |
Tidak bias | |
|
20% |
ft |
43,32162 |
27,10799 |
68.15299 |
Tidakbias |
|
ft |
1,04535 |
0,43056 |
1,15216 |
Tidak bias | |
|
0,93639 |
0.66437 |
1.01328 |
Tidak bias | ||
Tabel 14. Analisis Metode LAD-Bootstrap dengan B=1000 , SK= 95%
|
Persettfase Penohn |
Parameter |
Eslinusi |
Sehng Kepercayan 95% |
Keterangan | |
|
Balas Bawah |
BatasAtas | ||||
|
MK |
ft |
4X90844 |
20.68882 |
54X3383 |
Tidaktna |
|
ft |
123405 |
0,6’377 |
1.40895 |
Tidakbhs | |
|
ft |
1.01’64 |
0.63523 |
1.18414 |
Tidakbis | |
|
MK |
ft |
4X83407 |
18.41196 |
57.45697 |
Tidakbhs |
|
ft |
1X3’81 |
0,63526 |
1.44746 |
Tidakbhs | |
|
ft |
0.94167 |
0.73341 |
138232 |
Tidakbiu | |
|
70S |
ft |
41.93689 |
36X939’ |
6833898 |
Tidakbhs |
|
ft |
1.04316 |
0.61906 |
1.46366 |
Tidakbhs | |
|
ft |
0.63031 |
0.48550 |
1.03441 |
Tidakbiis | |
Tabel 15. Analisis Metode LAD-Bootstrap dengan B=1000 , SK= 99%
|
Psnentaw pακilun |
ParaznrtCT |
Estnnasi |
Sdasij Kepenavaau 99% |
Keterangan | |
|
Bnlas Bawah |
BalasAtas | ||||
|
IOM |
h |
«,M! |
25.57769 |
62,62269 |
Tidakhias |
|
ft |
ur» |
0W! |
13256* |
Txlakbias | |
|
h |
0,72084 |
0.34372 |
0,99263 |
Tidakbtas | |
|
1!⅛ |
4MU«I |
20,18021 |
6822522 |
Txiakbtas | |
|
ft |
1,04*2? |
0,46212 |
1.52060 |
Tidak bias | |
|
01 |
0,52*93 |
024731 |
019623 |
Tidakbias | |
|
MM |
i’,ra’ |
22.862'5 |
70507*6 |
Tidakbtas | |
|
Pl |
1.34966 |
0.459)3 |
152359 |
Txlakbus | |
|
0,63904 |
035345 |
0.90237 |
Txlakbias | ||
Pada Tabel 10, 11, 12, 13, 14, dan 15, menunjukkan bahwa data yang mengandung pencilan sebesar 10%, 15%, 20% yang telah dianalisis dengan metode LAD-Bootstrap bersifat tidak bias. Hal ini terlihat dari nilai parameter βo , βl dan β2 berada pada selang kepercayaan 95% dan 99%.
-
4.6 Perbandingan Hasil Analisis Metode MCD-Bootstrap dengan LAD-Bootstrap
Perbandingan antara hasil analisis metode MCD-Bootstrap dengan LAD-Bootstrap dapat dilihat dari bias parameter dan lebar selang kepercayaan yang diperoleh. Pada analisis MCD-Bootstrap dan LAD-Bootstrap sama-sama menghasilkan penduga parameter yang tidak bias pada data yang mengandung pencilan sebesar 10%, 15% ,dan 20% dengan
resampling sebanyak 500, 750, dan 1000 kali ulangan.
Selang kepercayaan yang digunakan sebesar 95% dan 99%. Selang kepercayaan yang dianggap mengandung nilai parameter sebenarnya terdiri dari batas bawah dan batas atas. Lebar selang kepercayaan dapat menjadi perbandingan ketepatan dari metode MCD-Bootstrap dan LAD-Bootstrap dalam mengatasi pencilan. Lebar selang diperoleh dari selisih batas atas dengan batas bawah yang dihasilkan oleh penduga parameter pada selang kepercayaan. Lebar selang yang pendek menunjukkan pendugaan yang lebih akurat. Demikian pula sebaliknya, lebar selang yang
panjang menunjukkan pendugaan yang kurang akurat. Lebar selang pada metode MCD-Bootstrap dan LAD-Bootstrap diuraikan pada tabel berikut ini:
Tabel 16. Lebar selang saat B= 500
|
Pasaitise Penttati |
Paianaa |
Selang Kepercayaan 95% |
Selang Kepercayaan 95% | ||
|
MCD-B<XXSH^ |
LAD-Bootifrap |
MCD- Soontrap |
LAD-βooκtrap | ||
|
M |
ft |
25.19479 |
28.045« |
3180226 |
37.045« |
|
P1 |
02 63S8 |
0,61157 |
032100 |
0,64350 | |
|
ft |
0,41002 |
0,54891 |
039634 |
0.64891 | |
|
15% |
ft |
29 52122 |
*3.045« |
3629345 |
37.04500 |
|
ft |
038456 |
0,91152 |
026186 |
1,01157 | |
|
ft |
0,46406 |
0,64891 |
0.60306 |
0.74891 | |
|
20% |
ft |
29,03021 |
40,045« |
3531176 |
36.14509 |
|
ft |
0.18200 |
0.95884 |
023377 |
0.89003 | |
|
ft |
0.44611 |
0,54891 |
0.48159 |
0.54891 | |
Tabel 17. Lebar selang saat B= 750
|
Persentase Pentilan |
Parameter |
Seiang Kepercay an95% |
Selang Keperayaar: 95% | ||
|
MCD-Saotitrap |
LAD-3oaaπφ |
MCD- BcKSrM |
LAD- Bccarrcgi | ||
|
10⅜ |
ft |
25,23323 |
2*04506 |
34,97404 |
35,04512 |
|
ft |
0,46140 |
M5777 |
0,30284 |
0.944'3 | |
|
ft |
030996 |
0.64891 |
0,42519 |
0.64891 | |
|
15% |
ft |
31.94821 |
3’24701 |
34.41892 |
37,60590 |
|
ft |
0,19369 |
0.68864 |
0,35394 |
0,63265 | |
|
ft |
0,47913 |
034891 |
0,50333 |
0.54891 | |
|
20% |
ft |
29.83315 |
47.0240* |
37.91640 |
41.04500 |
|
ft |
029782 |
0√0356 |
0,33888 |
0,72159 | |
|
ft |
036180 |
0.64891 |
0,45374 |
0,64891 | |
Tabel 18. Lebar selang saat B= 1000
|
Persrciase Pennlan |
PararnrtCT |
Selaag Keperayaan 95% |
Sdang Keperrayann 95% | ||
|
MCD-Booαtrφ |
LAD-Baotrrrap |
MCD- IiMBirap |
LAD- BiMBrrap | ||
|
IOM |
ft |
26,.'3479 |
34.14’33 |
34.83377 |
37.1249* |
|
ft |
0.36814 |
0.73518 |
0J0906 |
0.66861 | |
|
ft |
O.32∣X∣8 |
0.54891 |
0.42359 |
0.648911 | |
|
1,% |
ft |
31.19448 |
39.12918 |
41.64960 |
48204W |
|
ft |
030017 |
0.11219 |
026261 |
105848 | |
|
ft |
0.58492 |
0.64891 |
0.51456 |
0.64891 | |
|
20% |
ft |
29.80075 |
3’ 04522 |
38.59047 |
48.04576 |
|
ft |
0.20493 |
■.$4459 |
0.43373 |
1.06446 | |
|
ft |
0.36364 |
0.54891 |
0.47259 |
0.54891 | |
Berdasarkan Tabel 16, 17, dan 18 menunjukkan bahwa lebar selang yang dihasilkan oleh metode MCD-Bootstrap lebih pendek dibandingkan lebar selang yang dihasilkan oleh metode LAD-Bootstrap saat
resampling sebanyak 500, 750, dan 1000 kali ulanagan dan pada selang kepercayaan 95% dan 99% untuk penduga parameter βo , βl dan β2 .
Berdasarkan hasil analisis dan pembahasan, didapatkan kesimpulan sebagai berikut:
-
1. Metode MCD-Bootstrap dapat mengatasi pencilan pada data yang mengandung pencilan sebesar 10%, 15% dan 20%. Hal ini dapat dilihat dari metode ini menghasilkan penduga parameter yang tidak bias saat ulangan 500, 750, dan 1000 kali ulangan dan pada selang kepercayaan 95% dan 99%.
-
2. Metode LAD-Bootstrap dapat mengatasi pencilan pada data yang mengandung pencilan sebesar 10%, 15% dan 20%. Hal ini dapat dilihat dari metode ini menghasilkan penduga parameter yang tidak bias saat ulangan 500, 750, dan 1000 kali ulangan dan pada selang kepercayaan 95% dan 99%.
-
3. Keakuratan metode MCD-Bootstrap lebih tinggi dibandingkan metode
LAD-Bootstrap. Hal ini dapat ditunjukkan dari lebar selang yang dihasilkan oleh metode MCD-Bootstrap lebih pendek saat ulangan 500, 750, dan 1000 kali.
Adapun saran yang diberikan pada penelitian ini adalah perlu dikakukan penelitian lebih lanjut untuk membandingkan metode robust yang lainnya seperti Least Trimmed Square (LTS), estimasi-M, estimasi-MM dalam mengatasi pengaruh pencilan pada data.
DAFTAR PUSTAKA
El-Salam, M. (2013). The Efeciency of Some Robust Ridge Regression for Handling Multicolinearity and Non-Normal Errors Problem. Vol.7, No.77, Hal. 3831-3846.
Hubert, M., & Debruyne, M. (2009). Minimum Covariance Determinant. WIREs
Computational Statistics, Vol.2, Hal.36-43.
Neter, J., Wasserman, W., & Kutner, M. (1997). Model Linear Terapan Buku I: Analisis Regresi Linear Sederhana. (Terjemahan Bambang Sumantri) Bandung: FMIPA-IPB.
Sprent, P. (1989). Applied Nonparametric Statistical Methods. New York: Chapman & Hall.
Sungkono, J. (2013). Resampling Bootstrap Pada R. Magistra No. 84, Hal. 47-54.
55
Discussion and feedback