PENYELESAIAN MULTI TRAVELING SALESMAN PROBLEM DENGAN ALGORITMA GENETIKA

Written by NI KADEK MAYULIANA, EKA N. KENCANA, LUH PUTU IDA HARINI
on January 20, 2017

E-Jurnal Matematika Vol. 6 (1) – pp. 1-6

ISSN: 2303-1751

PENYELSAIAN MULTI TRAVELING SALESMAN PROBLEM DENGAN ALGORITMA GENETIKA

Ni Kadek Mayuliana¹^§ , Eka N. Kencana², Luh Putu Ida Harini³

¹ Program Studi Matematika – Fakultas MIPA – Universitas Udayana Email: [email protected]
² Program Studi Matematika – Fakultas MIPA – Universitas Udayana Email: [email protected]
³ Program Studi Matematika – Fakultas MIPA – Universitas Udayana Email: [email protected]

^§ Corresponding Author

Abstract

Genetic algorithm is a part of heuristic algorithm which can be applied to solve various computational problems. This work is directed to study the performance of the genetic algorithm (GA) to solve Multi Traveling Salesmen Problem (multi-TSP). GA is simulated to determine the shortest route for 5 to 10 salesmen who travelled 10 to 30 cities. The performance of this algorithm is studied based on the minimum distance and the processing time required for 10 repetitions for each of cities-salesmen combination. The result showed that the minimum distance and the processing time of the GA increase consistently whenever the number of cities to visit increase. In addition, different number of sales who visited certain number of cities proved significantly affect the running time of GA, but did not prove significantly affect the minimum distance.

Keywords: Genetic Algorithm, Multi Traveling Salesman Problem, simulation

1 LATAR BELAKANG

Multi Traveling Salesmen Problem (multi-TSP) sebagai perluasan TSP (Carter & Ragsdale, 2006), merupakan jenis permasalahan optimasi integer dari m > 1 salesmen yang mengunjungi n > m kota sedemikian hingga masing-masing kota dikunjungi hanya sekali. Optimasi pada multi-TSP ditujukan agar total jarak rute yang ditempuh para sales minimal (Sedighpour et al, 2011). Secara matematis, permasalahan multi-TSP dapat dinyatakan melalui persamaan berikut:

nn

Z = minΣΣc_ij · x_ij (1)

i=1 j=1

dengan kendala-kendala

1. _iⁿ₌₁ xij = 1, untuk j = 2, · · · , n;
2. _jⁿ₌₁ xij = 1, untuk i = 2, · · · , n;
3. ∑n=₁ χi,1 ≤ m;
4. _iⁿ₌₁ x_1,j ≤ m; dan
5.

1 , bila salesman bergerak dari i ke j ; ^x^ij⁼ 0, bila salesman tidak bergerak.

Adanya kendala 1 dan 2 menjamin setiap node hanya dikunjungi sekali oleh seorang salesman dan kendala 3 serta 4 menjaga agar setiap salesman yang bergerak akan berangkat dan kembali dari dan ke node awal.

Salah satu teknik komputasi yang bisa digunakan untuk menyelesaikan permasalahan multi-TSP adalah

Algoritma Genetika (AG). Carter & Ragsdale (2006) menyatakan AG merupakan salah satu teknik pada kelompok heuristic algorithm yang mengadopsi teori evolusi dalam penyelesaian permasalahan optimasi. Pada AG, lazin ditemui proses seleksi, proses rekombinasi, dan proses mutasi untuk memperoleh kromosom terbaik sebagai representasi solusi permasalahan komputasi yang dihadapi.

Permasalahan komputasi diselesaikan AG dengan memodelkan ke dalam rangkaian kromosom (encoding), dilanjutkan dengan proses seleksi dan rekombinasi kromosom melalui teknik mutasi dan perpindahan silang gen (crossover) untuk menemukan kromosom terbaik. Proses diakhiri dengan melakukan decoding dari kromosom terbaik yang diperoleh sebagai solusinya.

Penelitian ini ditujukan untuk mengetahui kinerja AG dalam menyelesaikan permasalahan multi-TSP. Kinerja AG diukur dari waktu yang dibutuhkan untuk menemukan solusi jarak minimum yang ditempuh sejumlah salesman untuk mengunjungi sejumlah kota tujuan.

2 METODE PENELITIAN

Jenis & Sumber Data

Sebanyak m salesmen, m ∈ {5, · · · , 10} disimulasikan mengunjungi n kota, n ∈ {5, 10, · · · , 30}. Untuk setiap n, matriks segi D berukuran (n + 1)² dibangkitkan secara acak. Elemen-elemen D menunjukkan jarak an-tardua kota atau antara depot – titik awal atau titik akhir keberangkatan – dengan salah satu kota tujuan. Pada masing-masing kombinasi n-m dilakukan 10 kali

ulangan.

Tahapan Analisis

Tahapan analisis AG yang ingin diketahui kinerjanya dalam mencari solusi optimal persamaan (1) untuk masing-masing jumlah kota n yang disimulasikan, dilakukan melalui tahapan berikut:

1. Start
2. Untuk semua m, m = 5, • • • , 10
3. Bangkitkan matriks jarak D

(a) Ulangan ^ 1
(b) DBest ^ ∞
(c) While Ulangan ≤ 10 Do

• I ^ 1
• Input MaxI, Pc, Pmut
• While I ≤ MaxI Do

– Bangkitkan populasi kromosom

– Pilih kromosom terbaik

– Hitung d = Panjang Rute

– Jika d < DB_est maka DB_est = d

– I=I+1

4. End

dengan MaxI merupakan maksimum iterasi pada suatu proses, Pc merupakan nilai probabilitas crossover, Pmut merupakan nilai probabilitas mutasi dan D_Best merupakan jarak minimum yang diperoleh setiap iterasi.

Gambar 2. Ilustrasi Kromosom pada AG

Algorithm 1: GenChr → Generate Chromosome

Input: Jumlah kota = n; Jumlah sales = m; Ukuran

Populasi = N_pop

Output: Populasi kromosom K = {K1 , · · · , KN_pop }

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

K ← ∅; Ki ← ∅

for i ← 1 to Npop do

K1 ← ∅ // Kromosom bagian I

K2 ← ∅ // Kromosom bagian II

N1 ← n // Salin jumlah kota n ke N1 for i ← 1 to m - 1 do

Randomized R; R ∈ [0, N1 ]

K2 ← K2 ∪ R

N1 ← N1 - R

K2 ← K2 ∪ N1

i←0

while i ≤ n do

Randomized R; R ∈ [1, n]

if R ∈/ K1 then

K1 ← K1 ∪ R

i=i+1

Ki ← K1 ∪ K2

K ← K ∪ Ki

Kromosom dan Populasi

Mendefinisikan kromosom merupakan tahap awal dari aplikasi AG. Merujuk Haupt & Haupt (2004), kromosom tidak lain dari array nilai-nilai variabel yang akan dioptimisasikan. Sekelompok kromosom akan membentuk populasi. Pada penelitian ini ukuran populasi Npop ditetapkan 20 kromosom, dengan representasi kromosom dinyatakan menggunakan two-part chromosome technique yang diusulkan oleh Carter & Ragsdale (2006) seperti terlihat pada Gambar 1:

19 return K

Pembangkitan Matriks Jarak D

Elemen-elemen matriks jarak D(n+ι)(n+ι) untuk masing-masing n yang disimulasikan dibangkitkan secara acak. Matriks D dapat dinyatakan dalam bentuk:

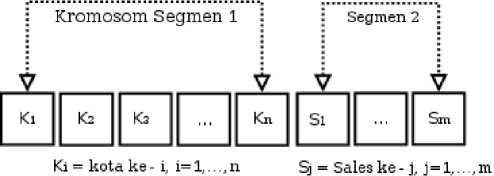
Gambar 1. Representasi Two-part Chromosomes

0

^d21

•••

d12 • •

0 •

••• ••

• d1(n+1)

• d2(n+1)

• • • •

^

^d(n+1)1

d(n+1)2 • •

•0

)

(2)

Pada (2), diagonal utama dari D bernilai 0 mempertimbangkan jarak dari sebuah kota ke dirinya = 0. Misalkan untuk 5 kota tujuan secara acak dibangkitkan matriks D berukuran 6 × 6 dengan d₁j menyatakan jarak dari titik awal keberangkatan (depot) ke kota tujuan, sebagai berikut:

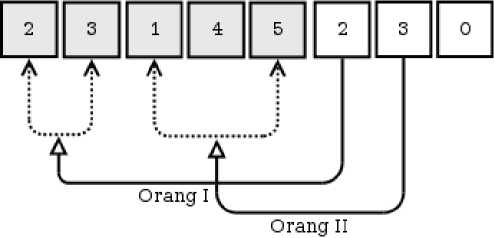
Sebagai ilustrasi, pada multi-TSP dengan 5 kota tujuan dan 3 salesmen, maka representasi kromosom di mana hanya 2 salesmen yang bergerak dengan orang pertama mengunjungi kota 2 dan 3 serta orang kedua mengunjungi kota 1, 4, dan 5 bisa ditunjukkan pada Gambar 2. Algoritma untuk membangkitkan Np_op kromosom untuk masing-masing kombinasi n — m diperlihatkan pada algoritma (1).

D6×6 =

⁰

2

3

4

7

¹

234

095

907

570

762

848

71

78

6 4

28

0 1

10

(3)

Pada Gambar 2, rute yang ditempuh orang I dan II adalah D–2–3–D dan D–1–4–5–D, dengan D menyatakan depot atau titik awal dan akhir keberangkatan.

Menggunakan kendala 5 pada persamaan (1), rute kedua sales dapat dinyatakan dalam matriks kehadiran X berikut:

X6×6 =

0

1

0

¹

11

00

000

010

1 00

0 00

0 01

000

(4)

Menggunakan matriks kehadiran X tersebut, maka jarak dari rute yang ditempuh kedua sales sebesar

Pemilihan Kromosom Elite

Sebelum dilakukan kawin silang (crossover) dan mutasi, sejumlah Nelite kromosom dipilih secara acak dari populasi awal. Proses pemilihan dilakukan menggunakan metode roulette wheel. Bila P_cum(i) ≤ Ri; i = 1, · · · , Npop dengan Ri menyatakan bilangan acak pada selang [0,1], maka kromosom ke-i terpilih sebagai anggota elite. Bila tidak, Ri lain dibangkitkan. Pada penelitian ini, proses diulangi sehingga jumlah kromosom yang terpilih Nelite = Npop = 20.

Proses Kawin Silang dan Mutasi

J arak

i=6 p=6

dij,∀xij = 1

i=1 j = 1

2+3+7+7+4+1+1

25.

Penghitungan Nilai Fitness

Fitness menunjukkan ukuran kelaikan dari sebuah kromosom. Pada penelitian ini, fitness kromosom ke-p dengan p = 1, · · · , N_pop dihitung menggunakan persamaan (5)

F itness_p = (5)

Sebagai ilustrasi, menggunakan persamaan (5), nilai fitness kromosom pada Gambar 2 = 25 = 0.04. Selanjutnya, masing-masing kromosom pada populasi awal berukuran 20 kromosom dihitung nilai fitness-nya dan peluang kumulatif (P_cum) dari kromosom ke-p dihitung menggunakan persamaan (6) untuk proses seleksi individu yang dilakukan pada tahap berikutnya.

Pii=P Fitness_i∑i=x° Fitnessi

Anggota kromosom populasi elite selanjutnya diseleksi untuk menentukan pasangan yang di-crossover-kan. Pada penelitian ini, teknik yang digunakan adalah Order 1 Crossover (OX1) mempertimbangkan kesederhanaan prosesnya. Jumlah kromosom yang mengalami kawin silang ditentukan sebesar N_cross bernilai genap dengan syarat 2 ≤ N_cross ≤ N_elite . Masing-masing pasangan kromosom diprogram hanya menghasilkan satu kromosom anak (offspring).

Pemilihan pasangan dilakukan dengan menetapkan probabilitas kawin silang Pc dan membangkitkan bilangan acak R untuk kromosom ke-i dari populasi elite. Bila R ≤ P_c , maka kromosom ke-i terpilih sebagai salah satu anggota pasangan. Anggota pasangan lainnya diperoleh dengan cara yang sama. Proses ini berhenti hingga seluruh kromosom pada populasi elite telah diperiksa. Gambar 3 memperlihatkan dua kromosom yang disilangkan dan offspring yang dihasilkan mengggunakan algoritma 2.

Kromosom offspring yang dihasilkan selanjutnya digabungkan ke dalam kelompok populasi elite. Bila masih terdapat kromosom induk yang belum dipasangkan, maka proses crossover diulangi, dan kromosom offspring yang dihasilkan juga digabungkan ke dalam kelompok elite sehingga di akhir proses ukuran popu-

Pcum (p)

(6)

.

lasi bertambah menjadi N_elite + Nc^^oss

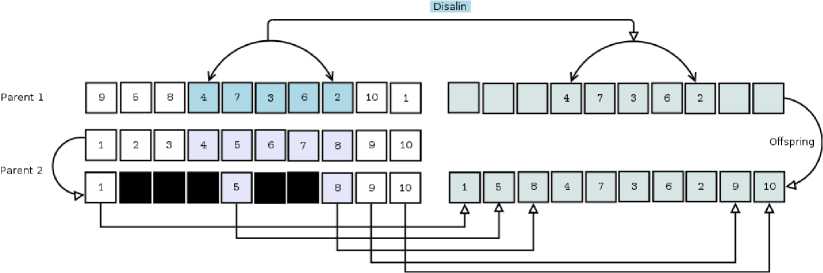
Gambar 3. Tahapan pada Order 1 Crossover

Proses terakhir yang dilakukan terhadap kromosom pada kelompok elite adalah proses mutasi, yang menurut Kumar et al. (2012) akan mencegah AG terperangkap pada penemuan solusi optimal yang bersifat lokal. Kromosom ke-i bermutasi bila nilai acak Ri yang dibangkitkan lebih kecil dari probabilitas mutasi (P_mut) yang pada penelitian ini ditetapkan sebesar 0.3

seperti disarankan oleh Tsujimura et al. (2001).

Penelitian ini mengaplikasikan teknik mutasi sisip (insertion mutation) pada kromosom yang terpilih. Teknik ini membangkitkan dua bilangan bulat acak – R₁ dan R₂ dengan syarat 1 ≤ R₁ < R₂ ≤ n. Selanjutnya, alel pada posisi gen R₁ dan R₂ saling dipertukarkan.

Sebagai ilustrasi mutasi sisip, misalkan R₁ dan R₂yang dibangkitkan untuk memutasi alel dari kromosom offspring pada gambar (3) adalah 5 dan 9. Maka mutasi sisip akan mengubah nilai gen offspring menjadi:

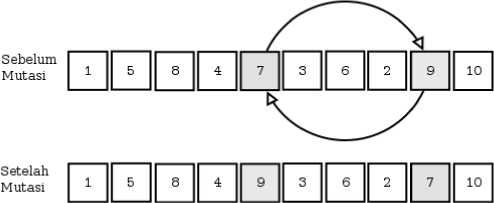
Gambar 4. Tahapan pada Mutasi Sisip

Algorithm 2: CrossChr → Ordered Crossover Input: Probabilitas Crossover=Pc , Pop. Orangtua Ci

Output: Elite baru C(i) = {C1, ∙ ∙ ∙ , CN_elite }

1 Cmating ← ∅; Repeat ← true; j ← 0
2 while Repeat do
3 for i ← 1 to Npop do
4 Randomized R // Bangkitkan bil. acak
5 if R < Pc then
6 j=j+1
⁷^C mating (j) ^ ^C mating (j) ∪ ^Ci

8 if j%2 = 0 then

9 Repeat ← f alse

10 for i ← 1 to (j - 1) do

ιι O(i) ^ 0 // Kromosom offspring ke-i

12 Randomized R₁, R₂; R₁ ,R₂ ∈ [1,length(K₁)]

13 if R₂ < R₁ then

14 |_ swap (R₁ ,R₂) // Tukar R₁ dengan R₂

/* Salin alel P₁ ke alel offspring */

15 for k ← 1 to length(Ki) do

16 if k ∈ [R₁ ,R₂] then

/* alel ke-k disalin ke offspring */

17 L ^θ(i,k) = Cik

18 else

¹⁹ L O(i,k) = 0

²⁰ _ O(i) ^ O(i) ∪ O(i,k)

/* Salin alel P2 ke alel offspring */

21 for k ÷- R₂ + 1 to length(K_i) do

²²^if^c(i+1,k) ∈ Oi ^then

²³ O(i,k) = ^c(i + 1,k)

24 k ← k + 1

25 for k ^ 1 to (R₁ + 1) do

26 if C(i+1,k) ∈ Oi then

²⁷ O(i,k) = ^c(i+1,k)

28 k ← k + 1

²⁹ O(i) ^ O(i)

³⁰ C(i) ^ ^C(i) ∪ O(i)

31 return C(_i)

3 HASIL SIMULASI

Untuk mengetahui kinerja AG dalam menemukan solusi optimal multi-TSP, dua indikator kinerja diamati yaitu (a) total jarak, dan (b) running time dari program Matlab yang dirancang.

Simulasi dirancang dengan proses crossover dan mutasi dilakukan pada kromosom segmen 1 dengan

tujuan jumlah kota yang dikunjungi salesman tidak berubah. Masing-masing kombinasi n - m direplikasi 10 kali dengan jumlah iterasi untuk memperoleh jarak minimum ditetapkan sebesar 200. Nilai-nilai P_cross dan Pmut yang digunakan masing-masing sebesar 0.5 dan 0.3.

Optimasi Jarak Minimum

Jarak minimum yang diperoleh untuk masing-masing kombinasi n - m dengan konfigurasi simulasi seperti uraian sebelumnya diperlihatkan pada Gambar 5:

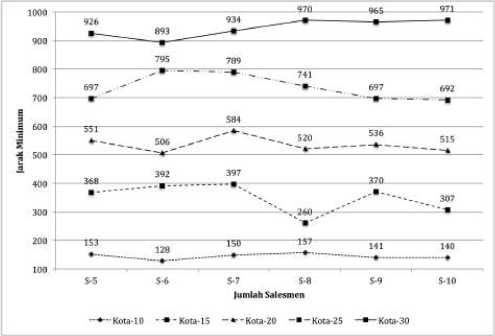
Gambar 5. Plot Jumlah Sales terhadap Jarak Minimum

Gambar 5 memperlihatkan semakin banyak jumlah kota n yang harus dikunjungi semakin besar jarak minimum yang diperoleh. Pada n = 10, AG memberikan hasil 128 satuan sebagai jarak minimum terkecil dari rute yang ditempuh saat m = 6, dan terbesar pada saat m = 8 dengan nilai 157. Pada n = 30, jarak minimum terkecil diperoleh saat m = 6 dan terbesar pada saat m = 10.

Secara deskriptif, tidak terlihat adanya pola kausal dari bertambahnya salesmen terhadap jarak minimum untuk jumlah kota m yang harus dikunjungi. Untuk mengkonfirmasi temuan tersebut, maka uji statistika dilakukan. Nilai rataan (x¯) jarak yang dihitung dari 10 ulangan untuk setiap kombinasi n - m digunakan dalam uji ini. Gambar 6 menunjukkan plot jumlah salesmen dengan rataan jarak rute.

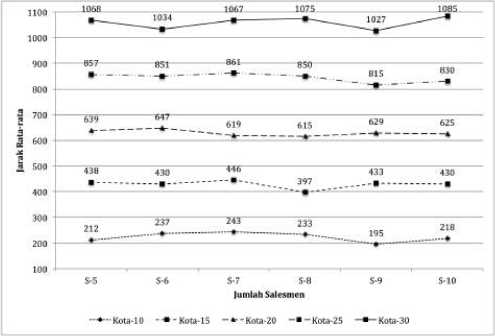
Gambar 6. Plot Jumlah Sales terhadap Rataan Jarak

Hasil uji Analysis of Variance (ANOVA) juga menunjukkan bertambahnya salesmen pada n yang sama tidak berpengaruh signifikan terhadap jarak rute. Uji ANOVA untuk masing-masing jarak ditunjukkan pada Tabel 1.

Merujuk hasil ANOVA pada Tabel 2, maka untuk 5 jumlah kota yang disimulasikan terbukti penambahan jumlah sales berpengaruh secara signifikan pada running time dari AG. Plot antara jumlah sales dengan running time rata-rata dari 10 ulangan diperlihatkan pada Gambar 8.

Tabel 1. ANOVA Pengaruh Jumlah Sales vs. Jarak Rata-rata

Jumlah	Nilai F	Nilai p	Keterangan
10 Kota	1.339	0.262	Tidak signifikan
15 Kota	1.143	0.349	Tidak signifikan
20 Kota	0.463	0.802	Tidak signifikan
25 Kota	0.764	0.579	Tidak signifikan
30 Kota	1.198	0.323	Tidak signifikan

Sumber: Data primer (2016), dianalisis.

Optimasi Running Time

Indikator kedua yang dianalisis dalam kinerja AG pada permasalahan multi-TSP adalah waktu (running time) yang diperlukan untuk menemukan solusi optimal pada masing-masing kombinasi n - m. Deskripsi waktu minimum diperlihatkan pada Gambar 7.

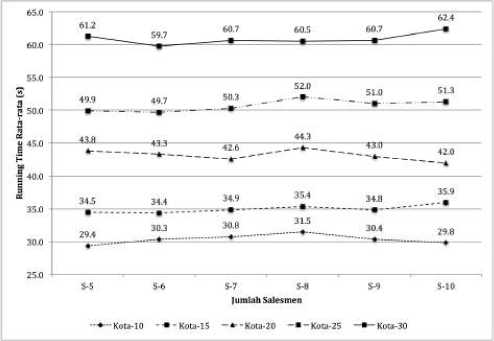
Gambar 8. Plot Jumlah Sales terhadap Waktu Rata-rata

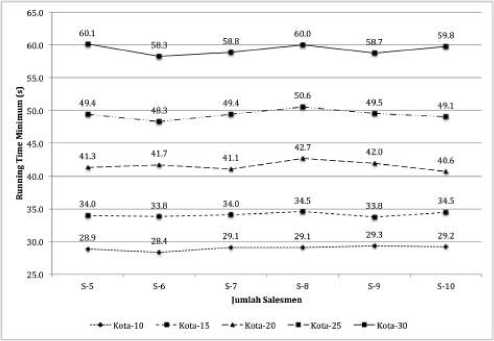
Gambar 7. Plot Jumlah Sales terhadap Waktu Minimum

Seperti halnya dengan indikator jarak rute, semakin besar jumlah kota (n) yang harus dikunjungi maka running time yang diperlukan untuk menemukan solusi optimum juga meningkat. Meski demikian, secara deskriptif terlihat bertambahnya salesmen tidak menjamin bertambahnya waktu eksekusi program.

Untuk mengetahui apakah terdapat perbedaan nyata secara statistika terhadap running time algoritma pada n tertentu untuk m yang berbeda, uji ANOVA pada rata-rata waktu running time dilakukan dengan hasil ditunjukkan pada Tabel 2.

Tabel 2. ANOVA Pengaruh Jumlah Sales vs Running Time

Jumlah	Nilai F	Nilai p	Keterangan
10 Kota	4.677	0.001	Signifikan
15 Kota	6.573	0.000	Signifikan
20 Kota	6.676	0.000	Signifikan
25 Kota	4.953	0.001	Signifikan
30 Kota	7.890	0.000	Signifikan

Sumber: Data Primer (2016)

4 SIMPULAN DAN SARAN

Simpulan

Penelitian yang ditujukan untuk mengetahui kinerja AG dalam menyolusikan permasalahan multi-TSP menyimpulkan:

1. Panjang rute terpendek yang diperoleh untuk n kota yang sama tidak dipengaruhi secara nyata oleh adanya penambahan tenaga salesmen dari nilai awal 5 orang hingga menjadi 10 orang. Hasil yang sama juga diperoleh bila yang dijadikan indikator adalah nilai rataan panjang rute terpendek yang diperoleh dari 10 ulangan simulasi;
2. Terdapat perbedaan yang signifikan pada perubahan running time dengan bertambahnya salesmen, meski tidak dapat disimpulkan bahwa pengaruhnya bersifat positif.

Saran

Penelitian ini merupakan penelitian awal tentang kinerja AG dalam mencari solusi dari multi-TSP melalui pengaturan lingkungan simulasi yang sederhana. Disarankan ada penelitian lanjutan untuk memodifikasi teknik crossover dan atau teknik mutasi yang digunakan dalam memilih populasi elite. Teknik partially mapped crossover (PMX) atau modified order crossover yang diusulkan oleh Sehrawat & Singh (2011) layak untuk diujicoba.

REFERENSI

Carter, A. E., C. T. Ragsdale. ”A new approach to solving the multiple traveling salesperson problem using genetic algorithms”, European Journal of Operational Research. No. 175, pp. 246-257, 2006.

Haupt, R. L., S. E. Haupt. ”Practical Genetic Algorithms”, 2nd. Ed. John Wiley & Sons, Inc. Canada. 2004.

N. Kumar, Karambir, R. Kumar, A Comparative Analysis of PMX, CX and OX Crossover operators for solving Travelling Salesman Problem, International Journal of Latest Research in Science and Technology. Vol. 1, No. 2, pp. 98-101, 2012.

Rostami, A. S, F. Mohanna, H. Keshavarz, A. A. R. Hosseinabadi. ”Solving Multiple Traveling Salesman Problem using the Gravitational Emulation Local Search Algorithm”, Applied Mathematics & Information Sciences. Vol. 9, No. 2, pp.699-709, 2015.

Sehrawat, M., S. Singh, ”Modified Order Crossover (OX) Operator”, International Journal on Computer

Science and Engineering (IJCSE), Vol. 3 No. 5 May, pp. 2019-2023, 2011.

Sedighpour, M., M. Yousefikhoshbakht, N. M. Darani. ”An Effective Genetic Algorithm for Solving the Multiple Traveling Salesman Problem”, Journal of Optimization in Industrial Engineering. No. 8, pp. 73-79, 2011.

S. Z. Selim, M. A. Ismail, K-means-type algorithm: generalized convergence theorem and characterization of local optimality, IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 6, No. 1, pp. 81-87, 1984.

Tsujimura, Y., Y. Mafune, M. Gen, ”Effects of Symbiotic Evolution in Genetic Algorithms for Job-Shop Scheduling”, Proceedings of the 34th Hawaii International Conference on System Sciences, pp. 1-7, 2001.

6