ANALISIS HUBUNGAN PRODUKSI PADI DAN INDIKATOR ENSO DI KABUPATEN TABANAN DENGAN PENDEKATAN COPULA
on
E-Jurnal Matematika Vol. 5 (4), November 2016, pp. 164-169
ISSN: 2303-1751
ANALISIS HUBUNGAN PRODUKSI PADI DAN INDIKATOR ENSO DI KABUPATEN TABANAN DENGAN PENDEKATAN COPULA
Luh Gede Udayani1§, I Wayan Sumarjaya2, Made Susilawati3
1Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: luhgedeudayani@gmail.com] 2Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id] 3Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: susilawati.made@gmail.com] §Corresponding Author
ABSTRACT
Dependence relationship between two or more variables is an issue that is often studied in the science of probability and statistics. Pearson correlation is often the easiest option to measure dependencies between variables. It is well known, that Pearson correlation assumes that the variable under study must be normally distributed. However, in reality this is not the case; for example, data in fields such as climatology and meteorology, insurance, and financial. Copula is a tool that can be used to model the joint distribution because it does not require the assumption of normality of the data so that it is resilient against a wide range of data. In this study, we discussed the application of copula in modeling the structure of dependencies between two variables: the production of rice and El-Nino Southern Oscillation (ENSO) indicator per period in Tabanan Regency. The best dependency model structure is given by the Frank copula of the Archimedean copula family with estimation parameter, θ = 2,817 and the loglikelihood value of 3,47.
Keywords: Archimedean copula, copula, ENSO, Frank copula, rice production
Hubungan kebergantungan (dependensi) antara dua variabel atau lebih merupakan salah satu persoalan yang dipelajari dalam ilmu probabilitas dan statistika. Selama ini, korelasi Pearson menjadi pilihan paling mudah dan sederhana yang digunakan untuk mengukur dependensi antarvariabel. Secara teoritis, korelasi Pearson mengasumsikan bahwa variabel harus berdistribusi normal. Namun, pada kenyataannya data tidaklah selalu berdistribusi normal seperti data pada bidang klimatologi dan meteorologi, asuransi, dan finansial.
Banyak distribusi bivariat atau multivariat yang dikembangkan sebagai alternatif untuk mengatasi kasus ketidaknormalan data pada distribusi marginal seperti bivariat gamma (Moran, 1969) dan (Nadarajah dan Gupta, 2006), Farlie Gumbel Morgenstern (Conway, 1979) dan eksponensial bivariat (Gumbel,
-
1960) . Namun, distribusi tersebut terbatas pada marginal yang sama. Oleh karena itu diperlukan metode yang dapat mengatasi permasalahan ini, salah satunya adalah dengan pendekatan copula.
Copula merupakan alat yang dapat digunakan untuk memodelkan distribusi bersama karena tidak mensyaratkan asumsi kenormalan dari data sehingga cukup fleksibel terhadap berbagai data.
Konsep copula pertama kali diperkenalkan pada tahun 1959 oleh seorang matematikawan bernama Abe Sklar. Copula merupakan suatu fungsi yang dapat menggabungkan beberapa distribusi marginal menjadi distribusi bersama.
Copula kemudian berkembang dan diaplikasikan dalam berbagai bidang misalnya bidang keuangan, asuransi, ekonometrika, dan deret waktu. Penelitian dengan pendekatan copula pada bidang hidrologi dilakukan oleh
Favre et al.(2004) dan Genest et al.(2007). Cherubini et al. (2004) dan McNeil et al. (2005) juga melakukan penelitian dengan pendekatan copula pada bidang keuangan dan asuransi. McNeil et al.membahas tentang pemodelan dependensi dengan copula dan aplikasinya dalam manajemen resiko untuk kasus data finansial yang berdistribusi heavytail. Copula dapat pula diaplikasikan pada bidang ekonometrika dan deret waktu, misalnya Patton (2009). Penelitian di bidang klimatologi dan meteorologi misalnya dilakukan oleh Vrac et al. (2005) dan Scholzel et al. (2008). Scholzel menjelaskan pola distribusi dan fungsi densitas dari variabel random multivariat pada data temperatur, curah hujan dan kecepatan angin.
Pada penelitian ini, dibahas aplikasi copula dalam memodelkan struktur dependensi antara dua variabel yaitu rata-rata produksi padi dengan indikator El-Nino Southern Oscillation (ENSO) per bulan di Kabupaten Tabanan.
Adapun tujuan dari penelitian ini, yaitu sebagai berikut:
-
1. Mengidentifikasi pola hubungan antara rata-rata produksi padi dan indikator ENSO di Kabupaten Tabanan dengan pendekatan copula.
-
2. Melakukan proses fitting copula sehingga didapatkan copula terbaik antara hubungan variabel rata-rata produksi padi di Kabupaten Tabanan (Y) dan variabel faktor iklim (ENSO) (X) dengan MLE.
Manfaat dari penelitian ini adalah bagi pengembang keilmuan dapat memahami metode Copula dan memodelkan hubungan antar variabel yang tidak berdistribusi normal dan terdapat data ekstrem.
Copula dapat dilihat melalui dua sudut pandang. Sudut pandang pertama copula sebagai fungsi yang menggabungkan atau memasangkan fungsi distribusi multivariat ke fungsi distribusi marginalnya, sedangkan sudut pandang kedua copula merupakan fungsi distribusi multivariat yang marginalnya adalah
uniform pada interval (0,1) (Nelsen, 2006).
Teorema Sklar adalah pusat dari teori copula dan menjadi dasar dari banyak teori statistika. Teorema Sklar mengembangkan copula dalam perannya membentuk distribusi multivariat dan distribusi marginalnya.
Misalkan H adalah suatu fungsi distribusi bersama dengan distribusi marginal F dan G. Maka terdapat sebuah copula C sedemikian hingga untuk setiapx,yER berlaku:
H(χ,y) = C(F(xλG(y)) (1)
Terdapat beberapa keluarga copula namun dua keluarga copula yang paling populer adalah copula Ellip dan copula Archimedean. Archimedean copula terdiri dari Frank copula, Clayton copula, Gumbel copula, Joe copula dan yang lainnya. Elliptical copula yang terdiri dari Gaussian copuladan copula-t.
Copula Gaussian
Copula Gaussian (Normal) merupakan salah satu keluarga Copula Elips. Copula Elips merupakan Copula yang berbentuk distribusi elips. Copula Gaussian diperoleh dari transformasi peubah acak ke distribusi normal standar. Vektor acak (XlrX2,-,Xm) memiliki fungsi distribusi kumulatif marginal, yaitu ^X i’ ^Xι> ’ ^Xm ,dengan ⅝ = ⅞∕¾>σ(o,ι) , maka setiap variabel komponen dapat ditransformasikan ke peubah acak yang berdistribusi normal standar seperti pada persamaan (2) berikut.
¾ = ^^‰u⅛M→ω^3 (2)
Denganj = ‰2, ■ ■■, m serta asumsi {zltz2,-tzm)τ berdistribusi multivariat normal standar N (P, ∑) dengan fungsi densitas peluang fN(OZ) dan matriks kovarians Σ. Berikut merupakan fungsi Copula Gaussian.
Copula Archimedean
Diberikan φ: [0j1] → [O,™] yang bersifat kontinu, menurun dan merupakan fungsi konveks sedemikian hingga ^(D = O dan φ(0) = ∞, maka invers dari φ adalah φ 1, dengan φ 1: [O,∞] → [0,1]. Fungsi Copula Archimedean C: [0,l]7n → [0,1] disajikan pada
persamaan berikut cGjPuI.....¾)
= φ^l (φ(u1) + φ(u2) + ∙∙∙ + φ(up))
(3)
denganφ≡[0,l] → [0,∞) adalah monoton sempurna, yaitu:
a*
(-l)k — Φ^1(u1) ≥ 0 ; fc ∈ N (4)
∂uλ
dan φ disebut generator Copula C dengan asumsi hanya memiliki satu parameter 5
(Nelsen, 2006).
Tahap awal copula dilakukan dengan mentransformasikan peubah acak ke domain [o,ι]. Distribusi marginal peubah acak X yang tidak diketahui, masing-masing adalah pada persamaan
Fx Cr) = ----V 1 (^w ≤ x);x ∈ fl (5) n + 1 A-J
J=ι
Proses transformasi dilakukan dengan cara membuat rank untuk masing-masing peubah acak. ^l ^τ'"τ‰^adalah rank dari ¾,-"j‰ kemudian masing-masing dibagi dengan n + 1.
Menurut Choros et al. (2010), ada beberapa cara estimasi parameter copula, salah satunya didapatkan dengan maximum likelihood estimation (MLE). Maximum likelihood estimation untuk copula ini diperoleh dengan memaksimumkan fungsi log likelihood.
Tabel 1. Estimasi Parameter Copula
|
Keluarga |
Estimasi $ I |
|
Clayton |
ffc , 2τ r^ S maka ⅞ τ i 1 — τ |
|
Gumbel |
1 ^ 1 r = 1 — — maka ¾ =--- ma a |
|
Frank |
4 τ=l-√l-⅛(β)) C ⅛⅛) = fungsi Debye |
|
Joe |
4 f = i+-d7⅛) DiW = . du |
|
Gaussian |
2 „ πf τ — — arcsin θ maka θ = sinf—) ιr ς ? j |
Sumber: Embrechts, Lindskog & McNeil, 2001
Setelah mendapatkan nilai estimasi parameter dengan pendekatan MLE, selanjutnya dilakukan pengujian estimasi untuk mengetahui parameter mana yang signifikan. Pengujian hipotesis copula adalah sebagai berikut.
hq-.c = cθ
H1-. C ≠ Ce
dengan Ce merupakan model dari Copula yang diasumsikan. Di bawah hipotesis nol dengan beberapa peubah acak yang mengikuti Copula Ce∕⅛→ΛΓ(O,l) adalah distribusi normal standar (Wang, 2010). Hipotesis yang dapat digunakan adalah sebagai berikut.
H0=Θ = θa
H1-. fl ≠ ⅞
Statistik uji:
§
^ sf(^θ) (6)
Daerah penolakan : ∑∖ > ^1.Ξ atau
p — value < a
Jika tolak H^ maka data mengikuti model Copula yang diasumsikan.
Data yang digunakan dalam penelitian ini adalah data sekunder diperoleh dari Dinas Pertanian Provinsi Bali dan The National Oceanic and Atmospheric yang dapat diakses melalui http://noaasis.noaa.gov/NOAASIS/.
Data rata-rata produksi padi dan indikator ENSO 3.4 masing-masing dengan 36 pengamatan bulan Januari hingga Desember dari periode 2013-2015. Penelitian dilakukan di Kabupaten Tabanan yang merupakan salah satu daerah penghasil padi terbesar di Bali.
Penelitian ini menggunakan data rata-rata produksi padi (Ton/Ha) per bulan sebagai variabel (Y), dan indikator ENSO (El Nino-Southern Oscilliation) yaitu anomali Sea Surface Temperature (SST) Nino 3.4 sebagai variabel (X).
Tahap-tahap analisis data dalam penelitian ini adalah sebagai berikut.
-
1. Mendeskripsikan data variabel rata-rata produksi padi dan SST Nino 3.4 dengan diagram dan grafik serta menguji asumsi distribusi normal dengan uji Kolmogorov
Smirnov pada data rata-rata produksi padi dan SST Nino 3.4.
-
2. Melakukan identifikasi hubungan antara rata-rata produksi padi (Y) dan SST Nino 3.4 (X)
-
a. Membuat scatterplot antara variabel rata-rata produksi padi (Y) dan variabel SST Nino 3.4 (X)
-
b. Menghitung nilai korelasi antara variabel rata-rata produksi padi (Y) dan variabel SST Nino 3.4 (X) dengan
korelasi Pearson.
-
3. Melakukan identifikasi pola hubungan antara rata-rata produksi padi (Y) dan variabel SST Nino 3.4 (X) dengan
pendekatan copula.
-
a. Menghitung copula empiris.
-
b. Melakukan transformasi data ke
domain [0,1] sebelum dilakukan
analisis dependensi dengan copula.
-
c. Membuat scatterplot hasil transformasi antara variabel rata-rata produksi padi (Y) dan variabel SST Nino 3.4 (X)
-
d. Mendapatkan estimasi parameter copula.
-
e. Fittingcopula dan mendapatkan copula terbaik antara hubungan variabel rata-rata produksi padi (Y) dan variabel SST Nino 3.4 (X) dengan MLE.
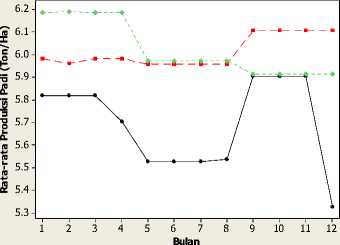
Sebesar 28 persen wilayah Kabupaten Tabanan merupakan lahan persawahan. Kabupaten Tabanan adalah daerah lumbung padi terbesar di Bali dengan produksi padi mencapai 194.121 ton pada tahun 2015. Gambaran perkembangan produksi padi di Kabupaten Tabanan selengkapnya ditunjukkan pada Gambar 1.
Rata-rata Produksi Padi Tiap Bulan Tahun 2013-2015
Variable
• 2013
■ 2014
2015
Gambar 1. Produksi Padi Tiap Bulan Tahun 2013-2015
Berita Resmi Statistik (2016) menyatakan produksi padi di kabupaten Tabanan tahun 2015 mengalami penurunan dibandingkan tahun 2014. Secara umum ada beberapa faktor penyebab penurunan produksi padi di Tabanan selama tahun 2015, antara lain adanya perbaikan jaringan irigasi pada tahun 2014 yang menyebabkan kekurangan luas tanam, adanya pergeseran atau tunda tanam di beberapa lokasi serta kemarau panjang sebagai akibat dari terjadinya El-Nino.
Tabel 2. Koefisien Korelasi Pearson, Kendall dan Spearman
|
Pearson |
Kendall | |
|
Correlation |
0,308 |
0,282 |
|
p-value |
0,068 |
0,016 |
Tabel 2 menunjukkan bahwa analisis hubungan dengan korelasi Pearson dan Tau Kendall tidak signifikan pada ff = 0.05 . Jika dilihat dari nilai koefisien korelasinya, berdasarkan tabel interpetasi koefisien korelasi versi De Vaus (2002), koefisien korelasi untuk Pearson menandakan terdapat kekuatan hubungan moderat sedangkan untuk Tau Kendall menandakan terdapat hubungan yang lemah antara rata-rata produksi padi dan SST Nino 3.4. Oleh karena itu dilakukan analisis hubungan copula untuk mengetahui keeratan hubungan rata-rata produksi padi dan SST Nino 3.4.
Tabel 3. Uji Normalitas Data dengan Kolmogorov Smirnov
|
Variabel |
Nilai KS |
p-value |
|
Rata-rata Produksi Padi |
0,240 |
<0,010 |
|
Anomali SST Nino 3.4 |
0,175 |
<0,010 |
Tabel 3 menunjukkan bahwa produksi padi memiliki p-value kurang dari a = 0,05 ini berarti bahwa data tidak berdistribusi normal. Begitu pula data Anomali SST Nino 3.4 tidak berdistribusi normal, karena menghasilkan nilai p-value kurang dari a = 0,05 . Oleh karena kedua data tidak berdistribusi normal, maka analisis korelasi Pearson tidak dapat digunakan oleh karena itu dilakukan analisis lebih lanjut dengan analisis hubungan copula untuk mengetahui keeratan hubungan produksi padi dan SST Nino 3.4.
Sebelum menghitung estimasi parameter Copula, tahap pertama yang dilakukan adalah membuat scatterplot transformasi peubah acak ke domain Uniform [0,1].
Pada analisis copula ini yang digunakan adalah Copula Frank, Clayton, Gumbel, Joe dan Gaussian. Estimasi parameter β dan nilai log likelihood dihitung untuk mengetahui model struktur dependensi yang terbaik pada copula. Hasil perhitungan pada copula Archimedean yang meliputi keluarga Frank, Clayton, Gumbel, dan Joe serta copula Gaussian diperoleh sebagai berikut.
Tabel 4. Hasil Estimasi Parameter Copula
|
Copula |
Estimasi Parameter |
^hit |
|
Frank |
2,712 |
16,845 |
|
Clayton |
0,784 |
2,306 |
|
Gumbel |
1,392 |
8,188 |
|
Joe |
1,704 |
7,747 |
|
Gaussian |
0,428 |
3,425 |
Estimasi parameter yang signifikan antara rata-rata produksi padi dengan SST Nino 3.4 adalah copula Frank, copula Gumbel, copula Clayton, copula Joe dan Gaussian karena
.
Tabel 5. Proses Fitting Copula
|
Jenis Copula |
Estimasi Parameter |
LogLikelihood |
|
Frank |
2,817 |
3,47 |
|
Clayton |
0,696 |
2,876 |
|
Gumbel |
1,265 |
1,232 |
|
Joe |
1,22 |
0,28 |
|
Gaussian |
0,417 |
2,57 |
5.
Berdasarkan hasil Tabel 5, maka model terbaik ditunjukkan oleh nilai log likelihood yang paling besar, yaitu model copula Frank. Dengan demikian dapat disimpulkan bahwa model yang tepat untuk menjelaskan struktur dependensi antara variabel produksi padi dan SST Nino 3.4 adalah model copula Archimedean pada keluarga Frank yang tidak memiliki kebergantungan ekor (tail dependence), yang berarti bahwa kejadian ekstrim pada anomali SST Nino 3.4 tidak berpengaruh terhadap kenaikan atau penurunan produksi padi.
Indentifikasi hubungan antara produksi padi di Tabanan dan indikator ENSO yaitu anomali SST Nino 3.4 menggunakan korelasi Pearson, dan Tau Kendall tidak dapat menjelaskan hubungan baik, hal ini ditunjukkan dari hasil nilai koefisien yang kecil. Berdasarkan pendekatan copula yang dilakukan menghasilkan hubungan yang lebih spesifik antar kedua variabel. Hal ini ditunjukkan pada pengujian dependensi copula yang signifikan. Sebagian besar mengikuti Copula Frank yang tidak memiliki tail dependensi yang berarti bahwa kejadian ekstrim pada anomali SST Nino 3.4 tidak berpengaruh terhadap kenaikan atau penurunan rata-rata produksi padi.
Saran yang dapat direkomendasikan untuk penelitian selanjutnya adalah menggunakan jumlah data yang lebih besar, menggunakan pendekatan nonparametrik, mengkaji identifikasi hubungan dengan keluarga copula lain selain Archimedean copula dan Gaussian copula, serta melakukan tindak lanjut penerapan copula di bidang lain seperti asuransi.
DAFTAR PUSTAKA
BPS. (2016). Berita Resmi Statistik Provinsi Bali, No. 46/07/51/Th.X. Bali: Badan Pusat Statistik.
Cherubini, U., Luciano, E. and Vecchiato, W. (2004).Copula Methods in Finance, Wiley.
Conway, D.A. (1979). Farlie-Gumbel-Morgestern Distributions. In : Encyclopedia of Statistical Sciences, 3, S.Kotz and N.L. Johnson, editor (John Wiley and Sons, New York), 28-31.
De Vaus, D. A., (2002)., Survey in Social Research, fifth edition., Allen and Unwin: New South Wales., p. 259.
Embrechts, P., F. Lindskog, A. McNeil. (2001). Modeling Dependence with Copulas and Applications to Risk Management. Handbook of Heavy Tailed Distributions in Finance, ed. S. Rachev, San Diego: Elsevier.
Favre, A.-C., S. El Adlouni, L. Perreault, N. Thi´emonge and B. Bobee.
(2004).“Multivariate Hydrological
Frequency Analysis Using Copulas.” Water Resources Research (40)
Genest, C., Favre A. – C., B´eliveau, J. and Jacques, C. (2007). “Metaelliptical Copulasand their Use in Frequency Analysis of Multivariate Hydrological Data.” WaterResources Research 43(9)
Gumbel, E.J. (1960). Bivariate Exponential Distributions. Journal of The American Statistical Association,55,698-707.
McNeil, A.J., Frey, R. and Embrechts, P. (2005), “Quantitative Risk Management: Concepts,Techniques”, Tools. Princeton
University Press, Princeton.
Nadarajah, S. dan Gupta, A. K. (2006). Some Bivariate Gamma Distributions, Applied Mathematics Letters, 19(8), 767-774.
Nelsen, R. B. (2006), “An Introduction to
Copulas”, Springer, New York, 2nd edn.
Wang, A. (2010). Goodness-of-Fit Tests For Archimedean Copula Models. Statistica Sinica , 441-453.
169
Discussion and feedback