PERAMALAN JUMLAH KUNJUNGAN WISATAWAN MANCANEGARA YANG BEKUNJUNG KE BALI MENGGUNAKAN FUNGSI TRANSFER
on
E-Jurnal Matematika Vol. 5 (4), November 2016, pp. 139-147
ISSN: 2303-1751
PERAMALAN JUMLAH KUNJUNGAN WISATAWAN MANCANEGARA YANG BEKUNJUNG KE BALI MENGGUNAKAN FUNGSI TRANSFER
I Ketut Putra Adnyana1§, I Wayan Sumarjaya2§, I Komang Gde Sukarsa3
1Jurusan Matematika, Fakultas FMIPA – Universitas Udayana [Email: adnyanaputra63@gmail.com]
2Jurusan Matematika, Fakultas FMIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id]
3Jurusan Matematika, Fakultas FMIPA – Universitas Udayana [Email: sukarsakomang@yahoo.com] §Corresponding Author
ABSTRACT
The aim of this research is to model and forecast the number of tourist arrivals to Bali using transfer function model based on exchange rate USD to IDR from January 2009 to December 2015. Transfer function model is a multivariate time series model which can be used to identify the effect of the exchange rate to the number of tourist arrivals to Bali. The first stage in transfer function modeling is identification of ARIMA model in exchange rate USD to IDR variable. The best ARIMA model is chosen based on the smallest Akaike information criterion (AIC). The next stage are as follows identification of transfer function model, estimation of transfer function model, and diagnostic checking for transfer function model. The estimated transfer function model suggests that the number of tourist arrivals to Bali is affected by the exchange rate of the previous eight months. The mean absolute percentage error (MAPE) is equal of the forecasting model to 9,62%.
Keywords: ARIMA, Transfer Function Model, Exchange Rate, Tourist Arrivals to Bali.
Peramalan adalah kegiatan untuk memperkirakan hal-hal yang akan terjadi pada masa yang akan datang. Peramalan pada umumnya digunakan untuk memprediksi sesuatu yang kemungkinan besar akan terjadi pada masa depan, menggunakan informasi data-data pada masa lalu. Untuk mendapatkan hasil ramalan yang baik maka diperlukan model yang tepat dari data yang dianalisis. Pemilihan metode peramalan harus dilakukan dengan teliti agar tingkat keakuratan hasil ramalan bisa dipertanggungjawabkan.
Deret waktu (time series) adalah analisis yang mempertimbangkan pengaruh waktu secara beruntun. Data-data yang dikumpulkan berdasarkan urutan waktu seperti, jam, hari, minggu, bulan, kuartal, dan tahun dapat dianalisis menggunakan metode deret waktu. Data deret waktu dapat dijadikan dasar dalam pengambilan keputusan untuk memperkirakan kejadian yang terjadi di masa yang akan datang.
Analisis deret waktu tidak hanya dapat dilakukan untuk satu variabel (univariat) tetapi juga dapat dilakukan lebih dari satu variabel (multivariat).
Model deret waktu yang paling populer dan banyak digunakan dalam peramalan deret waktu adalah model Autoregressive Integrated Moving Avarage (ARIMA). Model ARIMA merupakan gabungan dari metode pemulusan, metode regresi, dan metode dekomposisi yang digunakan untuk peramalan deret waktu model univariat. Untuk data deret waktu berganda tidak dapat dilakukan analisis menggunakan model ARIMA, oleh karena itu diperlukan model-model multivariat. Analisis deret waktu model multivariat antara lain model fungsi transfer (transfer function model), analisis intervensi (intervention analysis), Fourier analysis, analisis spectral, dan vector time series models (Wei, 2006).
Model fungsi transfer merupakan metode peramalan yang menggabungkan beberapa karakteristik dari model-model ARIMA dan
beberapa karakteristik analisis regresi. Tujuan dari model fungsi transfer adalah untuk mengidentifikasi dan menduga parameter fungsi transfer serta pengaruh lain yang disebut dengan gangguan yang ada berdasarkan pada nilai variabel takbebas dan variabel bebasnya (Wei, 2006). Model fungsi transfer dapat digunakan untuk mendapatkan penentuan ramalan ke depan secara simultan, salah satunya pada bidang pariwisata.
Pariwisata merupakan salah satu sektor utama dalam meningkatkan ekonomi pada suatu negara. Salah satu daerah di Indonesia yang mendapatkan imbas dari sektor pariwisata adalah Bali. Bali merupakan salah satu provinsi Indonesia yang berkembang dominan pada sektor pariwisata. Sebagian besar pendapatan penduduk Bali berasal dari industri pariwisata, sehingga tidak mengherankan industri pariwisata di Bali menjadi pilar pertumbuhan ekonomi. Mengingat semakin mudah promosi yang bisa dilakukan dengan kemajuan teknologi sekarang, sangat mungkin pariwisata di Bali akan berkembang sehingga dapat meningkatkan jumlah kunjungan wisatawan.
Motivasi seseorang dalam melakukan perjalanan wisata sangat dipengaruhi oleh pendapatan, harga atau kurs, kualitas, hubungan politik antara dua negara, perubahan cuaca atau iklim, peraturan pemerintah, dan teknologi pengangkutan atau transportasi (Yoeti, 1985, p. 69). Kurs atau nilai tukar sangat berpengaruh dalam perjalanan wisata, seseorang akan mempertimbangkan perjalanan wisata terkait dengan kurs. Dengan demikian persiapan dalam melakukan perjalanan wisata terhadap biaya yang dikeluarkan dan harga-harga pariwisata dapat dipertimbangkan. Semakin besar nilai tukar mata uang suatu negara terhadap rupiah, maka kecenderungan warga negara tersebut untuk melakukan perjalanan wisata semakin besar.
Penelitian yang telah dilakukan mengenai metode fungsi transfer adalah pemodelan jumlah penderita HIV/AIDS terkait kunjungan wisatawan di Kabupaten Badung dan Kota Denpasar (Wiradarma, 2011) dan penelitian yang dilakukan oleh Hasanah (2015) yaitu pada
pemodelan hubungan curah hujan dengan suhu dan kelembapan untuk meminimalkan kerugian yang diakibatkan bencana banjir.
Penelitian ini bertujuan untuk memodelkan dan memprediksi jumlah wisatawan mancanegara yang berkunjung ke Bali menggunakan fungsi transfer. Peramalan jumlah kunjungan wisatawan mancanegara ke Bali dilakukan berdasarkan nilai tukar (kurs) USD terhadap IDR.
-
2. KAJIAN PUSTAKA
Model Box – Jenkins (ARIMA)
Model ARIMA merupakan gabungan dari model ARMA (p,q) dan proses differencing, yaitu
φp (B)(1-B) d%t = (B) at (1)
dengan (B)(1-B) d^t merupakan deret pembeda sedangkan P,d, dan Q adalah bilangan bulat yang lebih besar atau sama dengan nol. Notasi P menunjukkan orde autoregresif (AR), d menunjukkan orde differencing, dan Q menunjukkan orde rerata bergerak (MA). Oleh karena itu secara umum model ini dinotasikan dengan ARIMA(P,d,Q).
Fungsi Korelasi Silang
Fungsi korelasi silang digunakan untuk
mengukur pengaruh dan arah antara dua
variabel acak. Menurut Wei (2006, p. 326) fungsi korelasi silang dinyatakan pada
persamaan berikut:
Pxy (k)=
Yxy (k) X^y
(2)
dengan k=0,±1,±2,±3,…
Notasi Yxy (k) menyatakan kovarians silang dari variabel x dan y, σx adalah simpangan baku dari variabel bebas dan σy adalah simpangan baku dari variabel takbebas.
Fungsi Transfer
Tujuan pemodelan fungsi transfer adalah untuk menetapkan model yang sederhana yang menghubungkan Yt dengan xt dan nt . Analisis fungsi transfer dilakukan melalui beberapa tahap yaitu: tahap identifikasi model,
pendugaan model fungsi transfer, dan pengujian diagnostik model. Menurut Wei (2006, p. 322), model fungsi transfer secara umum dilambangkan sebagai berikut:
yt =(B) xt + nt, (3)
dengan yt merupakan deret output, χt
merupakan deret input, nt adalah pengaruh kombinasi dari seluruh faktor yang memengaruhi yt (noise), dan V(B ) adalah koefisien pada model fungsi transfer dan disebut response impulse. Koefisien v(B) terdiri atas vo , V1 , V2,…,Vk , sedangkan k adalah orde fungsi transfer. Dalam fungsi transfer v(B) dapat ditulis dalam bentuk:
v(b)= § ( ) (4)
dengan
^s (B) = ω0 - ω1B-⋯-ωsBs ,
δr (B) =1-⅛(B)-⋯-δrBr,
dan b merupakan parameter kelambatan yang menggambarkan lag sebelum mendapatkan reaksi dari variabel bebas terhadap variabel takbebas.
Persamaan (3) dapat berubah sesuai dengan nilai b,s, dan nilai r pada fungsi transfer. Menurut Wei (2006, p. 324) beberapa aturan yang dapat digunakan untuk menduga nilai b,s,r dari suatu fungsi transfer:
-
a. Nilai b menyatakan bahwa yt tidak dipengaruhi oleh χt sampai periode t+b. Besarnya b dapat ditentukan dari lag yang pertama kali signifikan pada plot korelasi silang.
-
b. Nilai s menyatakan berapa lama deret output yt secara terus menerus dipengaruhi oleh xt-b-l, xt-b-2,…,xt-b-s sehingga dapat dikatakan bahwa nilai S adalah bilangan pada lag plot korelasi silang sebelum terjadinya pola menurun.
-
c. Nilai r menyatakan bahwa yt dipengaruhi oleh nilai-nilai masa lalu dari yt yaitu Vt-i, yt-2,…,Vt-r .
Identifikasi Model Fungsi Transfer
Identifikasi model fungsi transfer dilakukan melalui beberapa tahap. Wei (2006, p. 331)
menyatakan tahap-tahap identifikasi model fungsi transfer antara lain sebagai berikut:
-
1. Membuat deret masukan (input) menjadi white noise, dinotasikan dengan at dengan
persamaan
=
Φx (B) θx (B) t,
(5)
dengan at adalah deret white noise dengan rata-rata nol dan nilai varians σa .
-
2. Menghitung deret output dengan membuatnya menjadi white noise dengan model seperti di bawah ini:
Q Φx (B)
= (B) ■yt, (6)
-
3. Menghitung nilai korelasi silang ̂aβ (k) antara at dan βt untuk menduga Vk , dengan persamaan berikut:
̂k= ̂ ̂ aβ (k). (7)
oa
-
4. Mengidentifikasi b , untuk menduga nilai
v(B) dengan fungsi berikut:
|
̂( D)= ̂(B) r,b ̂( B)= ̂(B)B. |
(8) | |||
|
Untuk |
mengidentifikasi |
model |
noise, | |
|
perhitungan |
nilai |
duga |
deret |
noise |
|
dilambangkan sebagai | ||||
|
̂t= |
- ̂(B) xt |
= - |
̂(B) ̂(B) . |
(9) |
|
Kesesuaian |
model |
untuk |
noise |
dapat |
diidentifikasi dengan menguji sampel ACF dan PACF-nya atau dengan deret waktu univariat seperti pada persamaan berikut
Φ(B) nt =(B) at. (10)
Diagnostik Fungsi Transfer
Diagnostik model fungsi transfer dilakukan untuk menguji validitas model. Secara umum langkah-langkah diagnostik model fungsi transfer adalah sebagai berikut:
-
1. Pemeriksaan Autokorelasi Residual Model
Abraham dan Ledolter (1983, p. 344) menjelaskan bahwa pemeriksaan nilai residual dilakukan untuk mengetahui apakah nilai residual tersebut masih berkorelasi atau tidak. a) Hipotesis
Bq : = =⋯= =0; (tidak
terdapat korelasi antara residual)
Hy : minimal ada satu Pj ≠0, untuk j=1,2,…,k
-
b) Statistik Uji
So = m(m + 2)∑=ι(m-j)~1ρa(j) (11)
dengan <2 o adalah statistik uji Ljung-Box, p merupakan autokorelasi, K menyatakan banyaknya sisaan dan m adalah banyaknya parameter yang diduga. Statistik Q0
mengikuti distribusi χ2(K — p — q ) dengan p dan q adalah parameter dari model noise.
-
c) Kriteria pengambilan keputusan
Penolakan H0 dilakukan jika statistik uji Q0 >X2(K-p- q) atau penolakan H0 juga dapat dilakukan dengan melihat p-vaIue. Apabila p-value < a = 0,05 maka tolak yang artinya antar residual masih berkorelasi.
-
2. Penghitungan korelasi silang residual dengan input prewhitening
Prewhitening merupakan proses merubah deret masukan (input) menjadi white noise yang tidak berkorelasi. Langkah yang digunakan untuk memeriksa apakah deret input bebas, dilakukan dengan memeriksa korelasi silang antara komponen white noise deret noise (nt) dan deret input ( a t).
-
a) Hipotesis
H0 : tidak terdapat korelasi antara input dan residual
: terdapat korelasi antara input dan residual
-
b) Statistik Uji
Q 1 = m(m + 2) ∑^ 0(m-jY 1 p⅛ (j) (12) dengan statistik mengikuti distribusi (K + 1 — M'), m = n — t0 + 1 adalah
banyak residual dt dan M adalah
banyaknya parameter dan .
-
c) Kriteria pengambilan sampel
Penolakan dilakukan jika uji >
( + 1 — ) atau penolakan juga
bisa dilakukan dengan melihat - .
Apabila p- va Iue < a = 0,05 maka tolak yang artinya terdapat korelasi antar input dan output.
Jenis data yang digunakan dalam penelitian ini adalah data sekunder berupa data kunjungan
wisatawan mancanegara ke Bali (yt) yang diperoleh dari DISPARDA Provinsi Bali, kurs USD terhadap IDR (xt) yang diperoleh dari Bank Sentral Republik Indonesia (BI) pada situs www.bi.go.id. Data yang digunakan adalah data bulanan dari periode Januari 2009 – Desember 2015, dimana data in-sampel mulai Januari 2010 – Juni 2015 sebanyak 78 data, dan data out-sampel mulai Juli 2015 – Desember 2015 sebanyak 6 data.
Metode analisis data yang digunakan dalam penelitian ini adalah sebagai berikut:
-
1. Mempersiapkan deret input (kurs) dan output (jumlah wisatawan mancanegara);
-
2. Melakukan identifikasi pada plot data deret waktu, ACF, dan PACF dari deret input dan output. Dari ketiga plot ini, dapat dilihat apakah data yang ada telah stasioner atau belum. Jika tidak stasioner dalam mean maka dilakukan differencing, sedangkan jika tidak stasioner dalam varians maka dilakukan transformasi;
-
3. Menentukan model ARIMA untuk kurs;
-
4. Melakukan uji kesesuaian model dengan memenuhi asumsi white noise dan kenormalan.
-
5. Pemilihan model terbaik berdasarkan nilai AIC terkecil;
-
6. Melakukan prewhitening pada deret input untuk memperoleh a t;
-
7. Melakukan prewhitening pada deret output untuk memperoleh ;
-
8. Menghitung korelasi silang antara deret input dan output yang telah di prewhitening;
-
9. Menaksir bobot fungsi transfer;
-
10. Menetapkan nilai (b,s,r) yang menghubungkan deret input dan output untuk menduga model fungsi transfer;
-
11. Identifikasi deret noise;
-
12. Menetapkan (pn,qn) untuk model
ARIMA ( , 0, ) dari deret noise ;
-
13. Penaksiran parameter model fungsi
transfer;
-
14. Uji diagnostik model fungsi transfer dengan menghitung autokorelasi untuk nilai sisa model (b,s,r) yang menghubungkan deret
output dan deret input dan menghitung korelasi silang antara nilai sisa dengan residual (at) yang telah di prewhitening;
-
15. Meramalkan jumlah kunjungan wisatawan mancanegara ke Bali pada bulan Januari 2016 sampai Juni 2016 menggunakan fungsi transfer.
-
4. HASIL DAN PEMBAHASAN
Identifikasi Data Deret Waktu
Pada tahap ini, yang harus dilakukan yaitu membuat plot deret waktu dari deret input yaitu kurs dan deret output yaitu jumlah kunjungan wisatawan mancanegara ke Bali dari bulan Januari 2009 sampai Juni 2015. Langkah ini dilakukan untuk menunjukkan secara deskriptif bahwa data yang dianalisis adalah data berpola tren dan musiman. Hasil plot data kurs dan jumlah kunjungan wisatawan mancanegara ke Bali dapat dilihat pada Gambar 1 dan Gambar 2.
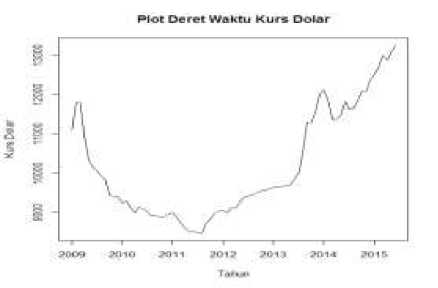
Gambar 1. Plot data kurs USD terhadap IDR
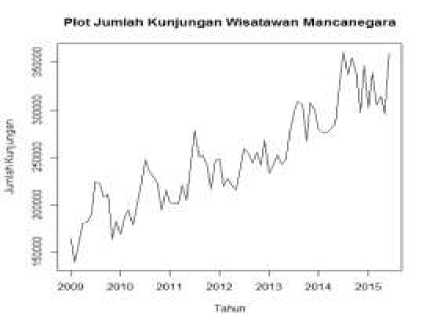
Gambar 2. Plot data jumlah kunjungan wisatawan mancanegara ke Bali
Berdasarkan Gambar 1 dan Gambar 2, terlihat bahwa data kurs dan jumlah kunjungan wisatawan ke Bali mengandung tren dan musiman. Gambar 1 menjelaskan bahwa nilai kurs mengalami tren menurun dari awal tahun 2009 sampai pertengahan tahun 2011, sedangkan menjelang tahun 2012 terjadi tren naik sampai akhir tahun 2015. Gambar 2 menjelaskan bahwa data jumlah kunjungan wisatawan mancanegara ke Bali yang cenderung meningkat setiap bulan, sedangkan pola musiman dilihat dari data pada setiap akhir tahun yang cenderung lebih besar pada tahun berikutnya.
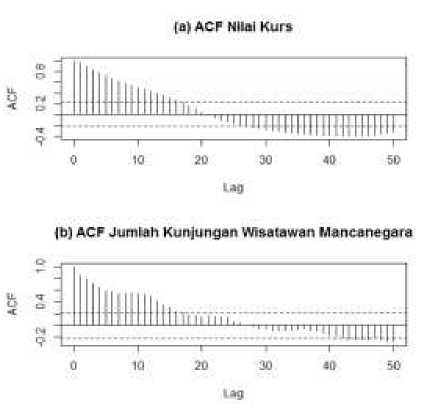
Gambar 3. (a) ACF Nilai Kurs dan (b) Jumlah Kunjungan Wisatawan Mancanegara
Pada Gambar 3 menunjukkan bahwa plot ACF cenderung turun lambat menuju nol, hal ini berarti bahwa pada data deret waktu nilai kurs dan jumlah kunjungan wisatawan mancanegara ke Bali tidak stasioner dalam mean, sehingga perlu dilakukan differencing terhadap tren dan musiman. Setelah kedua data deret input dan output stasioner, selanjutnya dilakukan penentuan orde model ARIMA untuk kurs.
Penentuan Model Arima untuk Kurs
Model dan orde ARIMA ditentukan dengan menghitung nilai ACF dan PACF dari data yang telah stasioner, yaitu data kurs yang telah di-differencing terhadap tren dan musiman. Selanjutnya ditentukan orde dari AR dan MA
nonmusiman serta menentukan orde dari AR dan MA musiman (seasonal). Dalam model, AR musiman biasanya ditulis dengan SAR dan MA musiman ditulis dengan SMA. Untuk menentukan orde masing-masing model, bisa dilihat pada plot ACF dan PACF pada Gambar 4.
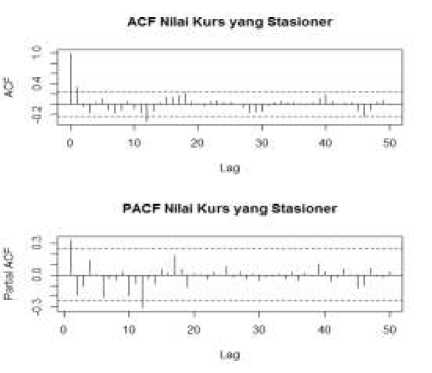
Gambar 4. Plot ACF dan PACF data Kurs yang
Stasioner
Dari plot ACF dan PACF data kurs yang stasioner, dipilih salah satu model terbaik berdasarkan nilai Akaike Information Criterion (AIC) terkecil. Nilai AIC dari setiap modelmodel sementara yang diperoleh dapat dilihat pada Tabel 1.
Tabel 1. Kriteria Pemilihan Model Terbaik
|
No. |
Model |
AIC |
|
1 |
ARIMA(0,1,1)(0,1,1)12 |
902,42 |
|
2 |
ARIMA(0,1,1)(1,1,1)12 |
902,85 |
|
3 |
ARIMA(1,1,0)(0,1,1)12 |
902,78 |
|
4 |
ARIMA(1,1,0)(1,1,1)12 |
903,56 |
Prewhitening Deret Input dan Deret Output
Pada langkah ini yang dilakukan adalah prewhitening deret input, dimana deret input kurs ( xt) dibuat menjadi white noise. Untuk deret input xt , modelnya dapat ditulis sebagai berikut:
«t = - 0,41«t-1 + 0,75at-12+0,31at-13 (14)
Setelah melakukan prewhitening deret input, selanjutnya dilakukan prewhitening deret output. Prewhitening deret output Vt diperoleh dengan cara melakukan transformasi yang sama dengan deret input xt , sehingga model deret output Vt dapat ditulis dalam bentuk:
βt = - 0,41Pt-I + 0,75Pt-u+0,31Pt-13 (15)
Penghitungan Korelasi Silang Deret Input dan Output yang telah di Prewhitening
Penghitungan korelasi silang digunakan untuk melihat keeratan hubungan antara deret input dan deret output. Gambar 5 menunjukkan korelasi silang antara deret input dengan deret output.
|
Korelasi Silang Lag Korelasi -1 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 0 -.11952 | . **| . |
|
|
Gambar 5. Plot korelasi Silang antara Deret |
Input dengan Deret Output
Kriteria pemilihan model terbaik pada Tabel 1 menunjukkan bahwa model ARIMA(0,1,1)(0,1,1)12 merupakan model terbaik, sebab memiliki nilai AIC terkecil yaitu 902,42. Model ARIMA(0,1,1) (0,1,1)12 dapat ditulis sebagai berikut:
(1-B)(1-B12) Zt=(1-Θ1B)(1-Θ1B12) at (13)
Gambar 5 menjelaskan lag yang pertama kali signifikan adalah lag ke-8, bahwa deret input kurs berpengaruh pada deret output jumlah kunjungan wisatawan mancanegara pada lag ke-8, yang menandakan pada waktu sebelumnya X belum memengaruhi y . Hal ini memiliki makna bahwa jumlah kunjungan wisatawan mancanegara ke Bali pada bulan ini memiliki keterkaitan secara linear dengan nilai kurs, delapan bulan sebelumnya.
Penaksiran Bobot Fungsi Transfer
Penaksiran bobot respon impuls diperoleh dari persamaan (7), adapun deviasi standar deret a sebesar 281,56, diperoleh dari hasil prewhitening deret input sedangkan untuk deret β sebesar 24882,3, diperoleh dari hasil prewhitening deret output. Hasil dari korelasi silang yang ada pada Gambar 5 dan nilai deviasi standar deret a dan deret β maka dengan menggunakan persamaan (6) diperoleh hasil perhitungan bobot respon impuls fungsi transfer adalah sebagai berikut: -10,56; 3,44; 4,87; -5,67; 5,35; -9,31; 15,59, -19,44; 25,86; -
18,06; 6,16; -10,56; 3,16; 7,81; -3,48; 2,77; -14,59.
Penetapan Nilai (b,s,r)
Dari hasil plot korelasi silang deret input dan deret output dapat diambil kesimpulan mengenai nilai (b,s,r) untuk model fungsi transfer yang menghubungkan deret input dan deret output sebagai berikut:
-
a. nilai b dapat ditentukan dari lag yang pertama kali signifikan pada plot korelasi silang, sehingga nilai b =8,
-
b. setelah lag ke-8, tidak terdapat lag-lag lain yang signifikan, sehingga s=0,
-
c. untuk r time lag selanjutnya, korelasi silang akan menunjukkan suatu pola yang jelas sehingga r=0.
Model fungsi transfer yang dipilih yaitu model dengan (b,s,r) = (8,0,0), sehingga persamaan dapat ditulis dalam bentuk:
v(B) xt = , (16)
atau bisa ditulis dalam bentuk:
yt = + ^t (17)
Identifikasi Deret noise
Langkah berikutnya adalah penaksiran awal deret noise (Tlf). Pada langkah sebelumnya diperoleh beberapa nilai taksiran bobot respon impuls, yang dapat digunakan untuk menghitung nilai dari deret noise (Tlf). Persamaan yang digunakan untuk menghitung nilai dari deret noise yaitu persamaan (9), sehingga:
Kt = -(v0xt + VιXt-ι + v2xt-2 +
v3xt-3 +⋯+vIbxt-Ib) (18)
Langkah selanjutnya yaitu memodelkan deret noise berdasarkan plot residual ACF dan PACF dari model fungsi transfer. Dalam menentukan model ARIMA deret noise, langkah-langkah yang dilakukan sama dengan penentuan model ARIMA deret input. Dari plot ACF dan PACF deret noise, maka diperoleh model fungsi transfer untuk masing-masing deret noise, yaitu:
-
a. ARIMA(0,0,1)(0,0,1)12
yt = +(1-Θ1B)(1-Θ1B12) at
-
b. ARIMA(1,0,1)(1,0,1)12
(1-Θ1B)(1-Θ1B12)
yt = +(1-ΦιB)(1-Φ1B12) at
-
c. ARIMA(0,0,1)(1,0,0)12
(1-Θ1B)
yt = +(1-Φ1B^) at
-
d. ARIMA(0,0,1)(1,0,1)12
yt =
(1-Θ1B)(1-Θ1B12)
+ (1-Φ1B12) at
-
e. ARIMA(1,0,1)(1,0,0)12
= (1-Θ1B)
yt = +(1-ΦιB)(1-Φ1B12) «t
Estimasi Parameter-parameter Model dari Model Fungsi Transfer
Pada langkah ini, akan diduga parameterparameter yang terdapat dalam model fungsi transfer. Model fungsi transfer dengan parameter yang telah diestimasi dapat dilihat pada persamaan berikut:
-
a. yt = 25,86Xt-B+(1-0,76B)(1 - 0,75B12) at
= v (ι-o,73B)(1-0,99B12)
-
b. yt = 25,86xt-8 "^" Z' -1 _1_A 1 ODUi _A -1 A θl2 λ Clfj
(1+0,12B)(1—0,19B^)
-
c. V = 25,6X +( « , 74B )
-
c. =25,6 +(1+0,59B12 )
= (1-0,77B)(1-0,99B12)
-
d. yt = 25,86xt-8 + (A _Λ17D12'∖
(1—0, )
e =2586 X +(I-Q, 58B )
-
e. = 25,86Xt-Q + 7
( 1+0,24B)(1+0,39B12)
Uji Diagnostik Model Fungsi Transfer
Pada langkah uji diagnostik model fungsi transfer dibagi menjadi dua sub-tahap sebagai berikut.
-
1. Penghitungan nilai autokorelasi untuk nilai residual model (b ,s,r) yang
menghubungkan deret input dan output.
Penghitungan nilai autokorelasi dilakukan untuk melihat apakah model fungsi transfer yang digunakan sudah cocok untuk data atau belum. Pada penghitungan autokorelasi menunjukkan bahwa untuk setiap lag, p-value bernilai lebih besar dibandingkan a = 0,05, sehingga residual fungsi transfer telah memenuhi asumsi white noise, atau tidak terdapat korelasi antar residual.
-
2. Penghitungan korelasi silang antara nilai residual dengan deret input
Pada penghitungan korelasi silang antara nilai residual dengan deret input, terlihat bahwa semua lag memiliki p-value yang lebih besar dari a = 0,05. Hal ini memperlihatkan bahwa residual model fungsi transfer dengan deret input telah memenuhi asumsi saling bebas.
Pemilihan Model Terbaik Berdasarkan Nilai AIC
Model fungsi transfer yang dipilih yaitu model yang mempunyai nilai AIC terkecil. Dari empat kandidat model fungsi transfer, model terbaik yang dipilih yaitu:
yt = 25,86%t_8 + (1 - 0,76B)(1 - 0,75B 1 2 )αt
Model ini memiliki nilai AIC terkecil yaitu 1275,741 dan nilai MAPE 9,62%. Nilai MAPE dari model fungsi transfer diatas sebesar 9,62% menunjukkan persentase kesalahan dalam meramalkan jumlah kunjungan wisatawan mancanegara terhadap pengaruh jumlah kurs.
Peramalan Jumlah Kunjungan Wisatawan Mancanegara
Hasil peramalan jumlah kunjungan wisatawan mancanegara berdasarkan model
fungsi transfer pada bulan Januari 2016 sampai Juni 2016 adalah sebagai berikut.
Tabel 2. Peramalan Jumlah Kunjungan Wisatatawan Mancanegara pada Bulan Januari 2016 – Juni 2016
|
Tahun |
Bulan |
Ramalan |
Aktual |
|
2016 |
Januari |
343124 |
350592 |
|
Februari |
352206 |
375744 | |
|
Maret |
346427 |
364113 | |
|
April |
347477 |
380767 | |
|
Mei |
344469 |
394557 | |
|
Juni |
385457 |
405835 |
Berdasarkan hasil dan pembahasan yang dilakukan, maka dapat disimpulkan bahwa model terbaik untuk peramalan jumlah kunjungan wisatawan mancanegara ke bali menggunakan fungsi transfer adalah:
yt = 25,86%t_8 + (1 - 0,76B)(1 - 0,75B 12) at
Hasil ramalan jumlah kunjungan wisatawan mancanegara yang berkunjung ke Bali dari Januari 2016 sampai Juni 2016 diperoleh hasil ramalan: 343124, 352206, 346427,347478, 344469, 385457.
Saran yang dapat diberikan dari hasil penelitian ini adalah pada penelitian yang akan datang untuk melakukan penelitian jumlah kunjungan wisatawan mancanegara ke Bali menggunakan metode lainnya yang nantinya bisa dibandingkan dengan penelitian ini.
DAFTAR PUSTAKA
Abraham, B., & Ledolter, J. (1983). Statistical
Methods for Forecasting. New Jersey: John Wiley and Sons.
Box, G., Jenkins, G., Reinsel, G., & Ljung, G.
-
(2016) . Time Series Analysis: Forecasting and Control (Fifth ed.). San Fransisco: John Wiley and Sons.
Disparda Provinsi Bali. (2016). Bali
Government Tourism Office. Retrieved Mei
1, 2016, from www.disparda.baliprov.go.id
Hasanah, Y. (2015). Pemodelan Curah Hujan Dengan Model Fungsi Transfer Input Ganda. Institut Pertanian Bogor.
Wei, W. W. (2006). Time Series Analysis: Univariate and Multivariate Methods (Second ed.). New York: Pearson Addison Wesley.
Wiradarma, N. P. (2011). Pemodelan Jumlah Penderita HIV/AIDS Terkait Kunjungan Wisatawan di Kabupaten Badung dan Kota Madya Denpasar dengan Metode Transfer Function. Institut Teknologi Sepuluh Nopember Surabaya.
Yoeti, O. A. (1985). Ilmu Pariwisata. Jakarta: Balai Pustaka.
147
Discussion and feedback