ESTIMASI MODEL REGRESI SEMIPARAMETRIK MENGGUNAKAN ESTIMATOR KERNEL UNIFORM (Studi Kasus: Pasien DBD di RS Puri Raharja)
on
E-Jurnal Matematika Vol. 4 (4), November 2015, pp. 176-180
ISSN: 2303-1751
ESTIMASI MODEL REGRESI SEMIPARAMETRIK MENGGUNAKAN ESTIMATOR KERNEL UNIFORM (Studi Kasus: Pasien DBD di RS Puri Raharja)
Anna Fitriani§1, I Gusti Ayu Made Srinadi2, Made Susilawati3
1Jurusan Matematika, Fakultas MIPA, Universitas Udayana [Email: annafitrianipangestu@gmail.com] 2Jurusan Matematika, Fakultas MIPA, Universitas Udayana [Email: srinadiigustiayumade@yahoo.co.id] 3Jurusan Matematika, Fakultas MIPA, Universitas Udayana [Email: susilawati.made@gmail.com] §Corresponding Author
ABSTRACT
Semiparametric regression model estimation is an estimation that combines both parametric and nonparametric regression model. In semiparametric regression, some of the variables are parametrics and the others are nonparametrics. Semiparametric regression is used when relationship pattern between independent and depentdent variables is half known and half unknown. Regression curve smoothing technique in nonparametric components in this study was using uniform kernel function. The optimal semiparametric regression curve estimation was obtained by optimal bandwidth. By choosing optimal bandwidth, we would obtain a smooth regression curve estimation in respect to data pattern. In choosing optimal bandwidth, we use minimum GCV as a criteria.The purpose of this study was to estimate the semiparametric regression function of dengue fever case using uniform kernel estimator. There were 6 independent variables namely age (in years) body temperature (in Celcius), heartbeat (in times/minutes) hematocryte ratio (in percent), amount of trombocyte (× 103/ul) and fever duration ( in days). Age, body temperature, heartbeat, amount of trombosyte and fever duration are parametric components and hematocryte ration is a nonparametric component. The optimal bandwidth (h) which was obtained with minimum GCVwas 0,005. The value of MSE which was obtained by using multiple linear regression analysis was 0,031 and by using semiparametric regression was 0,00437119.
Keywords: Semiparametric Regression, Kernel, Bandwidth, GCV
-
1. PENDAHULUAN
Pendekatan model regresi semiparametrik merupakan pendekatan model yang mengkombinasikan model regresi parametrik dan regresi nonparametrik. Pada regresi semiparametrik, sebagian variabel penjelasnya bersifat parametrik dan sebagian lain bersifat nonparametrik. Regresi semiparametrik
digunakan apabila pola hubungan antara sekumpulan variabel bebas dan variabel terikat ada yang diketahui dan ada pula yang tidak diketahui. Model regresi semiparametrik secara umum adalah:
Yi = Xiτ γ+ m(ti) + εi ; i = 1,2, .,.,n (1)
dengan yi adalah variabel respon ke-i, Xi adalah komponen parametrik ke-i, m(ti) adalah fungsi regresi ke-i yang tidak diketahui , dan εi adalah galat acak (random error) ke-i dimana εi~N(0, σ 2 ).
Salah satu teknik smoothing dalam model regresi nonparametrik adalah kernel. Penduga kernel fleksibel dan secara matematik mudah diselesaikan (Hai rdle [2]). Pada penduga kernel yang terpenting adalah pemilihan parameter pemulus (bandwidth) yang optimal untuk mendapatkan kurva regresi yang optimal. Pada penelitian ini akan dibahas bagaimana mengestimasi model regresi semiparametrik menggunakan estimator kernel uniform.
Selanjutnya menerapkan model regresi tersebut pada data pasien Demam Berdarah Dengue (DBD) selama dirawat di Rumah Sakit Puri Raharja Denpasar Bali berdasarkan lama kesembuhan pasien DBD. Sebaran data dari variabel yang diketahui bentuk kurva regresinya diduga menggunakan regresi parametrik, sedangkan peubah yang tidak diketahui bentuk kurva regresinya dapat diduga dengan regresi nonparametrik.
Metode statistika yang digunakan untuk mengetahui pola hubungan antara variabel bebas dengan variabel respon, dimana asumsi bentuk fungsi regresinya diketahui, disebut dengan regresi parametrik. Bentuk umum regresi linier ditulis sebagai
Vi = + Yjxi + εi ,i,j=1,2,..,n (2)
Dalam sebuah pengamatan, data tidak selalu memenuhi asumsi-asumsi yang mendasari uji-uji parametrik. Sehingga kerap kali dibutuhkan teknik inferensial yang tidak bergantung pada asumsi-asumsi parametrik. Dalam hal ini, teknik dalam regresi nonparametrik dapat digunakan, karena tetap valid walaupun tidak memenuhi asumsi-asumsi seperti asumsi kenormalan galat, kehomogenan, dan lain-lain. Bentuk umum model regresi nonparametrik adalah (Eubank [1]):
Yi = (ti)+εi ,i=1,2,…,n (3)
Yi adalah variabel respon ke-i, m( tt ) adalah fungsi regresi yang tidak diketahui bentuk kurva regresinya dan εi adalah error random atau galat acak yang diasumsikan independen dan identik dengan rataan 0 dan keragaman σ2 .
Regresi semiparametrik adalah gabungan dari regresi parametrik dan regresi nonparametrik, model regresinya dapat ditulis sebagai berikut
: = +m(ti)+εi ,i=1,2,…,n (4)
Yi adalah variabel respon ke-i, ^i adalah komponen parametrik, m(ti ) adalah fungsi regresi yang tidak diketahui bentuk kurva regresinya dan εi adalah galat acak dengan εi ~N (0, σ2).
Regresi kernel merupakan teknik nonparametrik dalam statistika untuk menduga fungsi regresi m(ti), Yi = (ti)+εi dengan
i=1,2,…,n. Penduga fungsi
semiparametrik adalah sebagai berikut:
̂(t)=∑wM (t) Yi
i=i
(7)
dengan
Whi (t)=
Kh (t-h) ∑?=i κh (t- ti)
1ℎ K( ‘ -ℎ =) ℎ∑^( -ℎ -)
±( l -ℎ = )ℎ ∑ ^iK (1 -ℎ k)
regresi
(8)
Penduga (8) diusulkan oleh Nadaraya dan Watson, sehingga penduga ini sering disebut penduga Nadaraya-Watson (Härdle [2]). Pada regresi kernel, ukuran penduganya ditentukan oleh bandwidth (h).
Parameter smoothing yang digunakan untuk mengontrol kemulusan dari kurva yang diestimasi disebut dengan bandwidth (ℎ). Proses pemilihan bandwidth yang sesuai (parameter smoothing) adalah bagian yang penting dari regresi nonparametrik. Permasalahan utama pada kernel smoothing bukan terletak pada pemilihan kernel tetapi pada pemilihan bandwidth (Hastie dan Tibshirani, [3]). Kurva yang under-smoothing yaitu sangat kasar dan fluktuatif karena nilai bandwidth yang terlalu kecil. Sebaliknya, kurva yang over-smoothing yaitu sangat mulus karena nilai bandwidth yang terlalu lebar. (Härdle [2]). Sehingga diperlukan bandwidth yang optimal untuk menghasilkan kurva optimal. Generalized Cross Validation (GCV) merupakan salah satu metode untuk mendapatkan h yang optimal (Eubank [1]), didefinisikan seperti berikut:
MSE
GCV(ℎ)= 7-----------V (9)
( tr (I-H(ℎ)))
dengan:
n
MSE=1 ∑(Yi - Wh (ti)) 2 (10)
i=i
Koefisien determinasi ( ) merupakan besaran yang digunakan untuk mengukur kelayakan model regresi dan menunjukkan besar kontribusi terhadap perubahan . Semakin tinggi nilai semakin baik model regresi yang terbentuk:
∑ (̂ ̅)
∑ ( ̅)
(11)
Nilai terletak antara 0 dan 1. Model dikatakan lebih baik jika semakin mendekati nilai 1.
Demam berdarah dengue merupakan penyakit yang disebabkan oleh virus dengue. Pada penderita demam berdarah dengue biasanya ditemukan perdarahan pada kulit, perdarahan dari gusi, hidung, usus, dan lain lain. Bila tidak ditangani segera, demam berdarah dengue dapat menyebabkan kematian. Selain menyebabkan demam berdarah dengue, inveksi virus dengue juga menyebabkan demam dengue. Setelah tergigit nyamuk pembawa virus, maka inkubasi akan berlangsung antara 3 sampai 15 hari sampai gejala demam dengue muncul. Adapun indikasi atau gejala demam berdarah adalah nyeri demam, suhu tubuh dan tekanan darah, dehidrasi, penurunan kadar trombosit, perdarahan, shock.
-
2. METODE PENELITIAN
Dalam penelitian ini data yang digunakan adalah data sekunder yang diambil di Rumah Sakit Puri Raharja Denpasar Bali. Populasi dari penelitian ini adalah pasien DBD yang pernah menjalani rawat inap di Rumah Sakit Puri Raharja. Sampel dari penelitian ini berasal dari data rekam medis pasien DBD periode bulan Januari sampai bulan Maret 2015. Peubah respons ( ) yaitu lama kesembuhan pasien DBD (hari) dan peubah bebas ( ) yaitu umur (U), suhu tubuh (S), nadi (N), trombosit (PLT), lama demam (LD) serta kadar hematokrit (HCT).
Dalam penelitian ini model regresi semiparametrik diduga menggunakan penduga (estimator) kernel dengan fungsi kernel uniform. Adapun langkah-langkah yang dilakukan adalah sebagai berikut:
-
a. Estimasi kurva regresi dengan pendekatan estimator kernel
-
- Mendefinisikan penduga γ untuk γ dan ̂ untuk pada model regresi
semiparametrik (4)
-
- Estimator m(t) dicari dengan
menggunakan persamaan (7) dan diperoleh model estimasi.
-
- Estimator γ dicari dengan menggunakan meminimumkan kuadrat galat dan diperoleh model estimasi.
-
b. Penentuan parameter pemulus
menggunakan fungsi kernel uniform dan ditentukan dengan GCV pada persamaan (9)
-
c. Menghitung penduga .
-
d. Menerapkan pada data sekunder.
-
e. Interpretasi model yang diperoleh.
Untuk menentukan komponen parametrik dan komponen nonparametrik, dapat dilihat dari plot masing-masing variabel bebas terhadap respon. Apabila plot antara variabel bebas dengan variabel respon memiliki hubungan linear, maka variabel bebas tersebut merupakan komponen parametrik. Namun, apabila plot antara variabel bebas dengan variabel respon tersebut memiliki hubungan nonlinier, dan sulit untuk menduga bentuk kurva regresinya, variabel bebas tersebut dipilih sebagai komponen nonparametriknya. Berikut
merupakan scatter plot dari masing-masing variabel bebas (umur, suhu tubuh, nadi, kadar hematokrit, trombosit, lama demam) terhadap respons (lama kesembuhan pasien DBD). Dengan bantuan software MINITAB 15 diperoleh plot sebagai berikut.
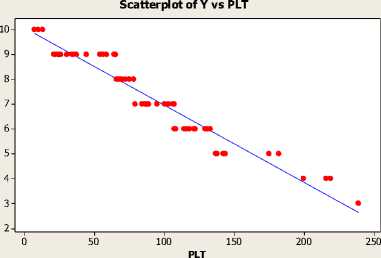
Gambar 4.1 Scatter plot Trombosit (PLT) dengan Lama kesembuhan pasien (Y)
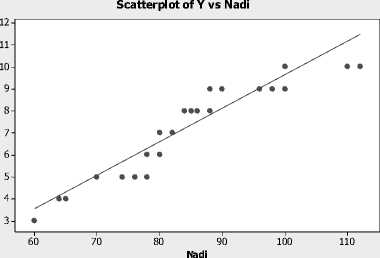
Gambar 4.2 Scatter plot antara Nadi (N) dengan Lama kesembuhan pasien (Y)
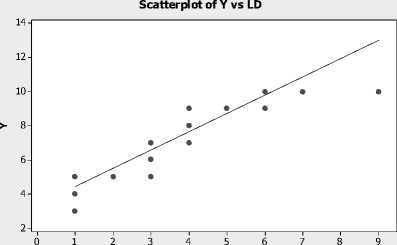
LD
Gambar 4.3. Scatter plot antara Lama demam (LD) dengan Lama kesembuhan pasien (Y)
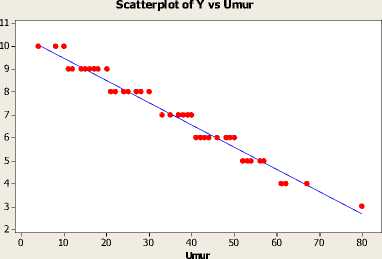
Gambar 4.4. Scatter plot antara Umur (U) dengan Lama kesembuhan pasien (Y)
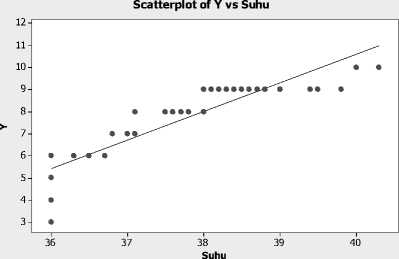
Gambar 4.5. Scatter plot antara Suhu (S) dengan Lama kesembuhan pasien (Y)
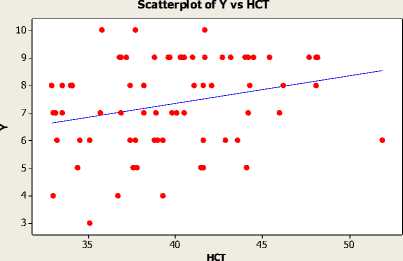
Gambar 4.6. Scatter plot antara Kadar hematokrit (HCT) dengan Lama kesembuhan pasien (Y)
Berdasarkan scatter plot diatas menunjukan bahwa variabel PLT, N, LD, U, dan S merupakan komponen parametrik dan HCT merupakan komponen nonparametrik.
Sebelum menentukan estimasi model regresi semiparametrik, akan dilakukan pendugaan kurva regresi semiparametrik yang optimal dengan menentukan ukuran bobot atau bandwidth (h) yang optimal. Pemilihan bandwidth yang optimal ditentukan berdasarkan kriteria nilai GCV yang minimum. Pemilihan bandwidth yang optimal akan menghasilkan pendugaan kurva regresi yang mulus sesuai dengan pola data. Bandwidth optimal pada penelitian diperoleh sebesar 0,005.
Penduga fungsi regresi semiparametrik dengan estimator kernel uniform ( ̂i), diperoleh dengan bantuan software R i386 2.15.0.
Pendugaan dapat dihitung setelah diperoleh ̂ pada komponen parametrik dan estimasi untuk komponen nonparametrik ( ̂ h(ti)).
-
4. KESIMPULAN
Regresi semiparametrik dengan estimator kernel uniform tidak memperoleh model estimasi secara eksplisit seperti regresi parametrik melainkan estimasi dari titik-titik amatan. Berdasarkan kriteria nilai MSE, regresi semiparametrik lebih bagus dibandingkan dengan analisis regresi linear berganda. Nilai MSE yang dihasilkan dengan regresi semiparametrik sebesar 0,00437119 lebih kecil dibandingkan nilai MSE yang dihasilkan dengan regresi linear berganda sebesar 0,031. Variabel yang signifikan dalam model regresi ini adalah suhu, umur, dan PLT sehingga dapat dikatakan bahwa dengan tingkat kepercayaan 1% variabel yang berpengaruh terhadap lama kesembuhan pasien adalah suhu, umur dan PLT. Estimasi model regresi semiparametrik yang diperoleh adalah sebagai berikut:
̂i = – 0,005495777 + 0,265938992 S – 0,472707138 U – 0,330655080 PLT + ̂■h (ti )
DAFTAR PUSTAKA
-
[1] Eubank, R. 1988. Spline Smoothing and Nonparametric Regression. Marcel Dekker. New York.
-
[2] Härdle, W. 1994. Applied
Nonparametric Regression. Cambridge University Press. New York.
-
[3] Hastie, T.J. and R.J. Tibshirani. 1990. Generalized Additive Models. Chapman and Hall. New York. London
180
Discussion and feedback