OPTIMALISASI PERENCANAAN PRODUKSI DENGAN PREEMPTIVE GOAL PROGRAMMING (STUDI KASUS: UD. DODOL MADE MERTA TEJAKULA, SINGARAJA)

E-Jurnal Matematika Vol. 4 (4), November 2015, pp. 201-207

ISSN: 2303-1751

OPTIMALISASI PERENCANAAN PRODUKSI DENGAN PREEMPTIVE GOAL PROGRAMMING

(STUDI KASUS: UD. DODOL MADE MERTA TEJAKULA, SINGARAJA)

Ni Putu Deviyanti^§1, Ni Ketut Tari Tastrawati², I Wayan Sumarjaya ³

¹Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: deviyantiniputu@gmail.com]

• ²Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: taritastrawati@yahoo.com]

• ³Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id] ^§Corresponding Author

ABSTRACT

One of the companies in production and marketing of dodol in Singaraja area is UD. Dodol Made Merta. This company produces four variants of dodol namely dodol merah, dodol kayu sugih, dodol ketan hitam, and dodol kacang. All the four dodol variants have a different demand levels.This aim of this research is to determine the optimal prediction of the amount of production that must be produced every month so that profit can be maximized by minimizing the cost of production. This research was done using two methods ARIMA. The best model for dodol merah is ARIMA (1,0,1), dodol kayu sugihis ARIMA(1,0,0), dodol ketan hitam is ARIMA (1,0,0) and dodol kacang is ARIMA(0.01).

Keywords: Time Series Stationer Model (AR, MA, ARMA), Time Series Non-Stasioner Model (ARIMA)

• 1.    PENDAHULUAN

Perencanaan dalam sebuah produksi merupakan salah satu hal yang harus diperhatikan dalam dunia usaha. Dalam dunia usaha, persaingan akan selalu dihadapi oleh pengusaha satu dengan pengusaha lainnya. Untuk dapat bertahan di tengah persaingan maka pengusaha perlu merancang dan membuat perencanaan yang matang dalam proses produksi maupun dalam proses pemasaran produk. Salah satu contoh kasus usaha yang belum merencanakan produksinya adalah usaha dagang yang bergerak dalam bidang produksi dodol di daerah Tejakula, Singaraja. Usaha ini memproduksi empat jenis varian dodol. Keempat jenis varian dodol tersebut adalah dodol merah, dodol kayu sugih, dodol ketan hitam, dan dodol kacang. Keempat varian dodol tersebut mempunyai tingkat permintaan yang berbeda-beda, dengan adanya tingkat permintaan

yang berbeda-beda ditambah dengan meningkatnya jumlah permintaan pada hari-hari tertentu maka perlu dilakukan suatu penelitian untuk memprediksi besar kecilnya jumlah produk yang harus diproduksi dalam setiap bulannya.

Penelitian ini menggunakan metode peramalan ARIMA. Rumusan masalah dalam penelitian ini adalah bagaimanakah model dan hasil prediksi jumlah permintaan keempat varian dodol yang harus diproduksi dalam bulan April dan Mei 2014 menggunakan metode ARIMA. Tujuan dari penelitian ini adalah untuk mengetahui model dan hasil prediksi jumlah permintaan keempat varian dodol yang harus diproduksi dalam bulan April dan Mei 2014 menggunakan metode ARIMA.

• 2.    KAJIAN PUSTAKA

  • 2.1    Konsep Dasar Peramalan

Peramalan (forecasting) adalah suatu seni dan ilmu untuk memperkirakan kejadian pada masa depan. Peramalan dilakukan dengan melibatkan pengambilan data masa lalu dan merubahnya ke masa yang akan datang dengan suatu bentuk model matematis (Heizer dan Render [1]). Pada dasarnya terdapat dua metode peramalan (Hakim [2]) yaitu:

• 1.    Metode Peramalan Kualitatif

Metode peramalan kualitatif digunakan ketika data historis tidak tersedia, dengan kata lain peramalan kualitatif merupakan peramalan yang tidak berbentuk angka. Metode peramalan kualitatif disebut juga metode subjektif.

• 2.    Metode Peramalan Kuantitatif

Metode peramalan kuantitatif menggunakan data historis atau data masa lampau. Metode peramalan kuantitatif dapat dibagi menjadi dua tipe yaitu (Hakim [2]):

• a.    Metode peramalan kausal meliputi penentuan faktor-faktor yang berhubungan dengan variabel yang diprediksi.

• b.    Metode peramalan deret waktu meliputi proyeksi dari nilai-nilai yang akan datang dari variabel yang sepenuhnya didasarkan pada observasi masa lalu dan masa kini variabel tersebut.

• 2.2    Konsep Deret Waktu

Data deret waktu adalah data yang disusun berdasarkan urutan terjadinya waktu. Data tersebut menggambarkan perkembangan suatu kejadian atau suatu kegiatan. Analisis deret waktu merupakan suatu metode kuantitatif yang mempelajari pola gerakan data masa lampau yang teratur (Wirawan [3]).

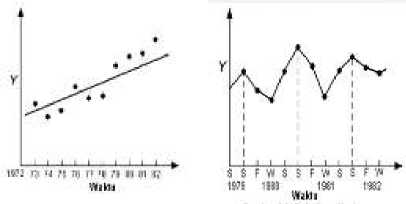
Deret waktu mempunyai empat komponen yaitu (Heizer dan Render [1]):

• a.    Komponen Tren adalah pergerakan data sedikit demi sedikit meningkat atau menurun, seperti perubahan pendapatan dan penyebaran umur.

• b.    Komponen Musiman adalah pola data yang berulang pada kurun watu tertentu, seperti harian, mingguan, bulanan, atau kuartalan.

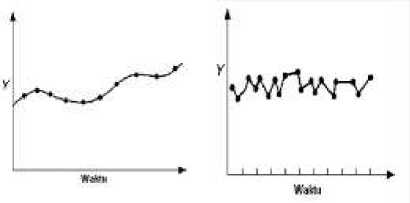
• c.    Komponen Siklis adalah pola dalam data yang terjadi setiap beberapa tahun.

• d.    Komponen Variasi Acak adalah satu titik khusus dalam data yang disebabkan oleh peluang dan situasi yang tidak biasa. Variasi acak tidak mempunyai pola khusus, jadi tidak dapat diprediksi.

(a)                     (b)

(c)

(d)

Gambar 1. Grafik Keempat Komponen, (a) Tren, (b) Musiman, (c) Siklis, (d) Variasi Acak

• 2.3    Model Deret Waktu

Model deret waktu dapat dibedakan menjadi dua yaitu model deret waktu stasioner dan model deret waktu non-stasioner.

Salah satu kelas proses stasioner deret waktu adalah proses ARMA (Autoregressive Moving Average). Proses ARMA ini meliputi proses AR (Autoregressive) dan proses MA (Moving Average) sebagai berikut:

• 1.    Proses AR (Autoregressive)

Proses autoregresif dengan tingkat P dinotasikan AR (P), memenuhi persamaan (Wei [4]):

Xt ⁼      + Φ2Xt-2 +⋯+ Φp%t-p + a_t (1)

dengan Φi adalah koefisien autoregresif untuk i=1,2,3,…,P , dan P adalah tingkat AR. Persamaan (1) dapat ditulis menggunakan operator backshift (B):

Xt ⁼      + φ2xt-2 +⋯+ Φp^t-p + at

Xt - Φ1Xt-1 - Φ2Xt-2-⋯- Φp^t-p ⁼

Xt ^- ΦιBX_t ^- Φ2B²X_t-₁-⋯- Φ_pB^pX_t-_p = (1-ΦιB - Φ2B²-⋯-Φ_pB^v) Xt =

d_t dapat dinyatakan dalam operator backshift (B) sebagai:

Φ_p (B) Xt = dengan

φ_p (B)=1-φ_iB - Φ2B²-⋯-Φ_pB^p .

• 2.    Proses MA (Moving Average)

Model moving average dengan tingkat Q dinotasikan MA (Q), adalah (Wei [4]):

Xt =   - Θ1^at-1 - B₂a_t-₂-⋯- ^q ^t-q (2)

dengan Bt adalah parameter model MA untuk i=1,2,3,…,Q,Q adalah tingkat MA. Persamaan (2) dapat ditulis menggunakan operator backshift B:

Xt =   - B1βt-1 - θ2^at-2 -⋯- ^q ^t-q

%t =  - θ₁Ba_t - θ₂B²a_t-₁-⋯- θ_qB^qa_t-_q

Xt =  (1-Θ₁B - B₂B²-⋯-B_qB*) (3)

cit dapat dinyatakan dalam operator backshift (B) sebagai:

Xt =   (B) dt

dengan

B_q (B)=1-Θ₁B - B₂B² -⋯-θ_qB*

• 3.    Proses ARMA

Model autoregressive moving average dengan tingkat P dan Q dinotasikan ARMA (P, ^cl), adalah (Wei [4]):

Xt ⁼      +⋯+ΦpXt-p + a_t - θιa_t-₁-⋯

• ^- ^q ^t-q                (4)

dengan Φi adalah koefisien autoregresif unuk i=1,2,3,…,P,P adalah tingkat AR, Bi adalah parameter MA ke-i untuk i=1,2,3,…,Q , dan Q adalah tingkat MA.

Menurut Wei [4], model rerata bergerak terintergrasi autoregresif dengan tingkat P,d, dan Q dinotasikan ARIMA ( P,d,Q), memenuhi persamaan:

Φ_p (B)(1-B)^dXt =   + B_q (B) a_t      (5)

dengan

Φ_p (B)=1-ΦιB - Φ2B² -⋯-Φ_pB^p

adalah koefisien AR (Autoregressive) dengan tingkat P,

B_q ⁽B)=1-Θ₁B ^- B₂B² -⋯-θ_qB*

adalah koefisiean MA (Moving Average) dengan tingkat Q,

(1-B)^dXt menyatakan proses differencing dengan tingkat d, Φ_p adalah koefisien AR (Autoregressive) dengan tingkat P , dan B_q adalah koefisien MA (Moving Average) dengan tingkat Q , dan Bq menyatakan rata-rata  (mean)  pada proses

ARIMA

Bq = (1-Φl-⋯-Φp).

Langkah-langkah yang dilakukan dalam analisis deret waktu adalah sebagai berikut (Rosadi [5]):   Langkah pertama adalah

identifikasi model. Identifikasi secara sederhana dilakukan dengan cara melihat plot dari data dengan tujuan untuk mengetahui apakah data sudah stasioner atau belum. Kestasioneran data dapat dilihat dari bentuk fungsi autokorelasi dan fungsi autokorelasi parsial. Apabila data belum stasioner dalam varians maka dilakukan transformasi Box-Cox dan apabila data deret waktu belum stasioner dalam rata-rata (mean) maka dilakukan proses differencing. Jika data sudah stasioner maka langkah selanjutnya adalah menduga dan menentukan bentuk model ARMA sesuai dengan proses differencing sehingga bentuk model ARMA yang diduga tersebut dapat menggambarkan sifat-sifat data dengan membandingkan plot ACF atau PACF dengan sifat-sifat fungsi ACF atau PACF dari model ARMA.

Setelah menduga dan menentukan bentuk model ARIMA maka, langkah selanjutnya adalah mengestimasi parameter dalam model. Untuk mengetahui apakah koefisien hasil estimasi signifikan atau tidak dapat digunakan pengujian statistik uji-t.

Langkah selanjutnya adalah melakukan pemeriksaan diagnostik dari model yang telah diestimasi. Untuk mengetahui apakah residual yang dihitung berdasarkan model yang telah diestimasi mengikuti galat dari model sifat white noise atau tidak, maka dilakukan pengujian sisaan white noise melalui nilai autokorelasinya.

Selanjutnya adalah pemilihan model terbaik. Parameter yang dipergunakan dalam peramalan

haruslah optimal untuk mendapatkan suatu model terbaik. Metode yang digunakan untuk mengetahui kualitas dari model adalah Akaike’s Information Criterion (AIC). Nilai AIC terkecil dapat mewakili model tersebut merupakan model terbaik. Persamaan untuk menghitung nilai AIC adalah sebagai berikut (Wei [4]):

(a)

(b)

ln AIC =   +ln

n

⁽n⁾

(6)

dengan k adalah banyaknya parameter dalam model, RSS adalah jumlah kuadrat residual dan n adalah banyaknya data residual.

Setelah mendapatkan model terbaik dari kandidat model yang diduga maka langkah selanjutnya adalah membuat model peramalan berdasarkan model ARIMA yang terpilih.

Langkah selanjutnya adalah menetukan peramalan. Setelah model peramalan ditentukan sesuai dengan model ARIMA yang terpilih, selanjutnya adalah melakukan peramalan dengan menggunakan bantuan program R.

(c)

(d)

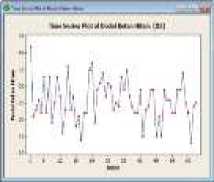
Gambar 2. Plot Deret Waktu (a) Varian Dodol Merah, (b) Varian Dodol Kayu Sugih, (c) Varian Dodol Ketan Hitam, (d) Varian Dodol Kacang

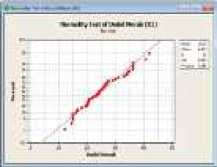
Langkah kedua yaitu membuat plot uji kenormalan:

• 3.    METODE PENELITIAN

Data yang digunakan adalah data sekunder diperoleh dari penjualan bulanan produksi dodol (kilogram) dari bulan Januari 2009 sampai Maret 2014.

Variabel yang digunakan dalam penelitian ini adalah data bulanan jumlah permintaan dari keempat varian dodol, besarnya keuntungan masing-masing dari keempat varian dodol, besarnya pemakaian dan kapasitas bahan baku, besarnya upah tenaga kerja, hasil peramalan jumlah permintaan keempat varian dodol, dan tujuan-tujuan yang ingin dicapai oleh usaha dagang menjadi urutan kepentingan prioritas.

• 4.    HASIL DAN PEMBAHASAN

Untuk mengetahui model dan hasil prediksi pada keempat varian dodol tersebut maka dilakukan langkah-langkah berikut: i. Identifikasi Model

Langkah pertama yaitu membuat plot deret waktu:

(b)

(a)

(c)

(d)

Gambar 3. Plot Uji Kenormalan (a) Varian Dodol Merah, (b) Varian Dodol Kayu Sugih, (c) Varian Dodol Ketan Hitam, (d) Varian Dodol Kacang

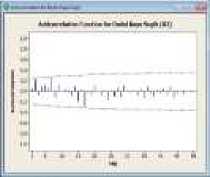
Langkah ketiga adalah membuat plot fungsi autokorelasi (ACF):

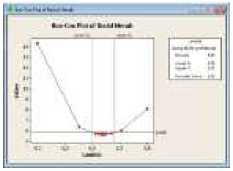
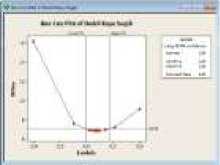
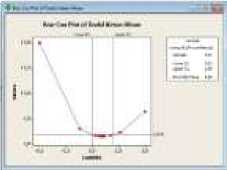
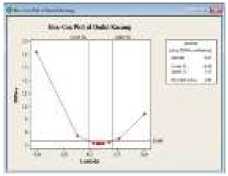
Langkah kelima adalah membuat plot transformasi Box-Cox:

(a)

(b)

(a)                           (b)

(c)

(d)

(c)                          (d)

Gambar 4. Plot ACF (a) Varian Dodol Merah, (b) Varian Dodol Kayu Sugih, (c) Varian Dodol Ketan Hitam, (d) Varian Dodol Kacang

Langkah keempat adalah membuat plot fungsi autokorelasi parsial (PACF):

(a)                        (b)

Gambar 6. Plot Transformasi Box-Cox (a) Varian Dodol Merah, (b) Varian Dodol Kayu Sugih, (c) Varian Dodol Ketan Hitam, (d) Varian Dodol Kacang

Langkah keenam adalah menduga bentuk model ARMA yang sesuai untuk data aktual sehingga diperoleh kandidat model ARIMA (1,0,1), ARIMA (0,0,1), dan ARIMA (1,0,1).

• ii.    Mengestimasi Parameter

Mengestimasi parameter dalam model dilakukan dengan bantuan program R sebagai berikut:

Tabel 1. Estimasi ARIMA untuk Permintaan Dodol Merah

(c)

(d)

Estimasi Parameter dalam Model	φ	θ	AIC
ARIMA(0,0,1)		0,0486	425,88
ARIMA(1,0,0)	0,0705		425,78
ARIMA (1,0,1)	0,8423	-0,7314	425,45

Gambar 5. Plot PACF (a) Varian Dodol Merah, (b) Varian Dodol Kayu Sugih, (c) Varian Dodol Ketan Hitam, (d) Varian Dodol Kacang

Tabel 2. Estimasi ARIMA untuk Permintaan Dodol Kayu Sugih

Estimasi Parameter dalam Model	φ	θ	AIC
ARIMA(0,0,1)		0,0321	431,09
ARIMA(1,0,0)	0,0464		431,04
ARIMA (1,0,1)	0,8750	-0,7869	431,28

Tabel 3. Estimasi ARIMA untuk Permintaan Dodol Ketan Hitam

Estimasi Parameter dalam Model	φ	θ	AIC
ARIMA(0,0,1)		0,0774	411,82
ARIMA(1,0,0)	0,0857		411,79
ARIMA (1,0,1)	0,15232	-0,0673	413,78

Tabel 4. Estimasi ARIMA untuk Permintaan Dodol Kacang

iv. Peramalan

Langkah selanjutnya adalah peramalan dari model ARIMA terbaik. Model ARIMA terbaik untuk peramalan enam bulan kedepan yaitu dari periode April sampai dengan September 2014 dapat dilihat pada tabel di bawah ini:

Tabel 5. Hasil Peramalan Model ARIMA

Periode April-September 2014 untuk Dodol Merah

Estimasi Parameter dalam Model	φ	θ	AIC
ARIMA(0,0,1)		-0,1099	416,53
ARIMA(1,0,0)	-0,0856		416,66
ARIMA (1,0,1)	0,8927	-1,000	416,99

• iii.    Pemeriksaan Diagnostik dan Pemilihan

Model Terbaik

Berdasarkan pada tabel estimasi parameter dalam model, maka diperoleh model terbaik untuk keempat varian dodol sebagai berikut: a. Model ARIMA (1,0,1) model terbaik untuk dodol merah, secara matematis dapat ditulis:

̂=Φ×t-1 + θa_t.₁ + a_t

̂= 0,0982Xt-ι - 0,7314 ^at-ι + a_t

• b.    Model ARIMA (1,0,0) model terbaik untuk dodol kayu sugih, secara matematis dapat ditulis:

̂=φX_t-ι + a_t

̂= 0,0464Xt-ι + a_t

• c.    Model ARIMA (1,0,0) model terbaik untuk dodol ketan hitam, secara matematis dapat ditulis:

̂=φXt-ι + a_t

̂= 0,0857Xt-ι + a_t

• d.    Model ARIMA (0,0,1) model terbaik untuk dodol kacang, secara matematis dapat ditulis:

⁼ θ^t-l + a_t

̂=- 0,1099a_t-ι + a_t

Nilai Peramalan	Bulan
	April	Mei	Juni	Juli	Agustus	September
	23,5	23,7	23,8	24	24,1	24,3

Tabel 6. Hasil Peramalan Model ARIMA

Periode April-September 2014 untuk Dodol Kayu Sugih

Nilai Peramalan	Bulan
	April	Mei	Juni	Juli	Agustus	September
	25,8	25,9	25,9	25,9	25,9	25,9

Tabel 7. Hasil Peramalan Model ARIMA

Periode April-September 2014 untuk Dodol Ketan Hitam

Nilai Peramalan	Bulan
	April	Mei	Juni	Juli	Agustus	September
	27,8	28,6	28,6	28,6	28,6	28,6

Tabel 8. Hasil Peramalan Model ARIMA

Periode April-September 2014 untuk Dodol Kacang

Nilai Peramalan	Bulan
	April	Mei	Juni	Juli	Agustus	September
	25,3	25,4	25,5	25,5	25,5	25,5

• 5. KESIMPULAN

Berdasarkan hasil penelitian dapat disimpulkan sebagai berikut:

• 1.    Model terbaik untuk keempat varian dodol adalah sebagai berikut untuk varian dodol merah diperoleh ARIMA (1,0,1), varian dodol kayu sugih adalah ARIMA (1,0,0) varian dodol ketan hitam diperoleh ARIMA (1,0,0), dan untuk varian dodol kacang diperoleh model terbaik adalah ARIMA (0,0,1).

• 2.    Selanjutnya, untuk hasil prediksi jumlah permintaan keempat varian dodol yang harus diproduksi dalam bulan April dan Mei 2014 adalah dodol merah sebesar 23,5 dan 23,7 kg, dodol kayu sugih adalah sebesar 25,8 dan 25,9kg, dodol ketan hitam diperoleh hasil sebesar 27,8 dan 28,6kg, dan dodol kacang sebesar 25,3 dan 25,4kg.

DAFTAR PUSTAKA

• [1]    Heizer, Jay dan Render, Barry. 2006.

Operations     Management.     Edisi

Ketujuh.Terjemahan:Dwianoegrahwati Setyoningsih dan Indra Almahdy. Jakarta: Selemba Empat

• [2]    Hakim, Abdul. 2004. Statistika Deskriptif untuk Ekonomi dan Bisnis. Yogyakarta: Ekonisia.

• [3]    Wirawan, Nata. 2001. Statistik 1 (Stastistik Deskriptif). Denpasar: Keraras emas.

• [4]    Wei, William W. S. 1990. Time Series Analysis Univariate and Multivariate Methods.Addison-Wesley     Publishing

Company, Inc. Canada.

• [5]    Rosadi, Dedi. 2012. Ekonomitrika dan Analisis Runtun Waktu Terapan dengan Eviews.Yogyakarta:Andi.

207