ESTIMASI NILAI CONDITIONAL VALUE AT RISK MENGGUNAKAN FUNGSI GAUSSIAN COPULA
on
E-Jurnal Matematika Vol. 4 (4), November 2015, pp. 188-194
ISSN: 2303-1751
ESTIMASI NILAI CONDITIONAL VALUE AT RISK MENGGUNAKAN FUNGSI GAUSSIAN COPULA
Herlina Hidayati§1, Komang Dharmawan2, I Wayan Sumarjaya3
1Jurusan Matematika, FMIPA – Universitas Udayana [Email: herlinadisanasini@gmail.com]
2Jurusan Matematika, FMIPA – Universitas Udayana [Email: dharmawan.komang@gmail.com]
3Jurusan Matematika, FMIPA – Universitas Udayana [Email: sumarjaya@unud.ac.id] §Corresponding Author
ABSTRACT
Copula is already widely used in financial assets, especially in risk management. It is due to the ability of copula, to capture the nonlinear dependence structure on multivariate assets. In addition, using copula function doesn’t require the assumption of normal distribution. There fore it is suitable to be applied to financial data. To manage a risk the necessary measurement tools can help mitigate the risks. One measure that can be used to measure risk is Value at Risk (VaR). Although VaR is very popular, it has several weaknesses. To overcome the weakness in VaR, an alternative risk measure called CVaR can be used. The porpose of this study is to estimate CVaR using Gaussian copula. The data we used are the closing price of Facebook and Twitter stocks. The results from the calculation using 90% confidence level showed that the risk that may be experienced is at 4,7%, for 95% confidence level it is at 6,1%, and for 99% confidence level it is at 10,6%.
Keywords: portfolio, copula, CVaR, Gaussian copula.
Pada saat ini, mengukur dan mengelola risiko pada data finansial sudah menjadi hal yang lumrah dilakukan dalam manajemen risiko. Salah satu strategi yang digunakan untuk mengelola suatu risiko yaitu dengan membentuk portofolio saham. Secara umum, mengolah suatu risiko sering kali mengacu pada struktur kebergantungan dari variabel acak tingkat pengembalian (return) harus memenuhi asumsi-asumsi seperti berdistribusi simetris, distribusi tingkat pengembalian (return) tidak memiliki ekor gemuk (heavy tail), serta hubungan antara variabel harus linear. Namun pada kasus finansial hal ini sangat sulit untuk dipenuhi sehingga diperlukan fungsi copula.
Copula memiliki konsep sebagai alat untuk mempelajari kebergantungan tidak linear antara kejadian dalam kasus multivariat. Keluarga copula yang populer antara lain keluarga copula eliptik dan keluarga Archimedian copula. Anggota dari keluarga copula eliptik adalah
Gaussian copula dan t-Student copula. Sedangkan anggota dari keluarga Archimedian copula adalah Clayton copula, Frank copula, dan Gumbel copula.
Untuk mengukur dan mengelola suatu risiko, diperlukan alat ukur yang dapat digunakan untuk mengukur risiko yang ada. Salah satu alat ukur yang dapat digunakan adalah Value at Risk (VaR). VaR merupakan salah satu bentuk pengukuran risiko yang cukup populer digunakan, namun VaR juga memiliki kelemahan antara lain VaR hanya mengukur persentil dari distribusi keuntungan atau kerugian tanpa memperhatikan setiap kerugian yang melebihi tingkat VaR, dan VaR tidak koheren karena tidak memiliki sifat sub-additive (Artzner, et al [1]). Untuk mengatasi kelemahan yang dimiliki VaR, maka diperlukan Conditional Value at Risk (CVaR).
CVaR merupakan suatu ukuran risiko yang memiliki banyak keunggulan di antaranya yaitu CVaR merupakan ukuran risiko yang koheren
serta bersifat convex dan sub-additive (Rockafellar and Uryasev [6]). Selain itu, CVaR juga mampu menghitung risiko pada data berdistribusi normal maupun tidak normal.
Penelitian ini membahas estimasi nilai Conditional Value at Risk menggunakan salah satu fungsi copula dari keluarga eliptik yaitu Gaussian copula. Saham yang digunakan pada penelitian ini yaitu saham Facebook dan saham Twitter.
2. METODE PENELITIAN
Return merupakan keuntungan atau hasil yang diperoleh oleh investor dari investasi yang dilakukan. Return dirumuskan sebagai berikut:
Rt =ln( ^ ) (1)
dengan R^ menyatakan tingkat pengembalian (return) saham pada periode ke-t, dan S^
menyatakan harga saham pada periode ke t (Sunaryo [7]).
Korelasi Kendall’s tau digunakan untuk mengukur kekuatan hubungan dua variabel. Data yang digunakan berskala ordinal dan tidak harus memenuhi distribusi normal. Pada Gaussian copula, Kendall’s tau ditulis sebagai berikut:
τ = arcsin (p) (2)
π
dengan p adalah koefisien korelasi Gaussian copula.
Copula pertama kali dipopulerkan oleh seorang matematikawan bernama Abe Sklar pada tahun 1959 yang teoremanya dikenal dengan nama Teorema Sklar. Copula memiliki beberapa keunggulan antara lain tidak memerlukan asumsi distribusi normal dan dapat menunjukkan adanya pola sebaran data pada ekor distribusi masing-masing variabel.
Salah satu keluarga copula yang populer digunakan adalah keluarga copula eliptik. Anggota keluarga copula eliptik adalah Gaussian copula dan t-Student copula.
1. Gaussian Copula
Gaussian copula merupakan salah satu jenis copula yang menggunakan distribusi normal standar bivariat. Gaussian copula dapat ditulis sebagai berikut (Embrechts, McNeil, and
Straumann [2]):
♦ ‘w
♦'*N
Q‰)- ∫ -T
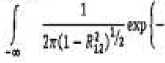
si-2J7llfl+tj∣
2(1-Φ i
2. t-Student Copula
t-Student copula merupakan salah satu jenis copula yang menggunakan distribusi t-Student bivariat. t-Student copula dapat ditulis sebagai berikut ((Embrechts, McNeil, and Straumann [2]):
⅞⅛> ⅞⅛ -,Vt2]<
. f S s1-2⅛st+?) 1
⅛i⅛*)~ J ] ^ ι niΛΓ^ W1—pi⅛ I i^ (5)
Value at Risk (VaR) merupakan suatu ukuran risiko yang menghitung besarnya kerugian maksimum yang mungkin dialami dalam suatu periode tertentu. VaR dapat didefinisikan sebagai berikut [4]:
VaR(a)=Fl1(a) (6) dengan Fl 1 (a) adalah invers suatu fungsi distribusi dari a.
Conditional Value at Risk (CVaR) merupakan suatu ukuran risiko yang memperhitungkan kerugian melebihi tingkat VaR. CVaR pada selang kepercayaan a ∈ [0,1] dapat ditulis sebagai berikut:
VaR(a)
-
a
(7)
dengan P(r) adalah fungsi densitas (Letmark [5]).
Langkah Analisis
Untuk menganalisis data portofolio, akan dilakukan langkah-langkah yaitu: (1) menghitung return saham Facebook dan saham Twitter; (2) mencari nilai statistik deskriptif dari return yang diperoleh; (3) memeriksa ada tidaknya sifat autokorelasi dan efek heteroscedasticity pada data return masing-masing saham. Jika data return memiliki sifat autokorelasi dan efek heteroscedasticity, maka perlu dilakukan penyaringan (filter) yang berguna untuk menghilangkan sifat tersebut dengan menggunakan model GARCH; (4)
memeriksa keberadaan nilai ekstrem dengan menggunakan Pareto tail; (5) mengestimasi parameter Gaussian copula; (6) melakukan simulasi Gaussian copula; Menggunakan Gaussian copula, selanjutnya (7) hitung nilai VaR dan (8) estimasi nilai CVaR dari saham portofolio. Setelah itu, (9) lakukan interpretasi dari hasil yang diperoleh.
Menghitung Return
Pada tahap ini diperoleh nilai return saham Facebook dan saham Twitter dengan mengolah data closing price menggunakan persamaan (1). Data return yang diperoleh kemudian disajikan ke dalam grafik yang dapat dilihat pada Gambar 1.
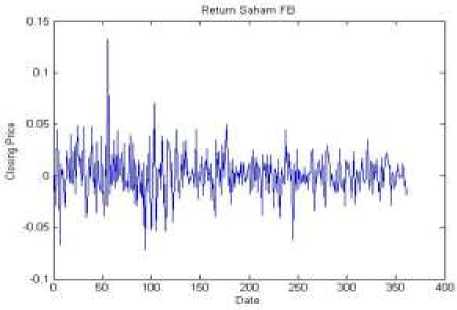

Gambar 1. Plot Return FB dan TWTR
Nilai Statistik Deskriptif
Nilai statistik deskriptif dari saham Facebook dan saham Twitter dapat dilihat pada Tabel 1.
Tabel 1. Nilai Statistik Deskriptif
|
FB |
TWTR | |
|
Mean |
1,6 × 10 - 3 |
1,04 × 10 - 3 |
|
Standard Deviation |
2,1 × 10 - 2 |
3,7 × 10 - 2 |
|
Skewness |
6,3 × 10 - 1 |
-4,3 × 10 - 1 |
|
Kurtosis |
8,4 |
12,03 |
Pada Tabel 1 dapat dilihat bahwa return saham Facebook dan saham Twitter tidak berdistribusi normal. Secara empiris, data berdistribusi normal dapat dilihat dari nilai skewness dan kurtosis. Sebagai acuan nilai skewness pada data berdistribusi normal bernilai nol, sedangkan kurtosis pada data berdistribusi normal bernilai tiga.
Tabel 1 menunjukkan nilai skewness pada return saham Facebook diperoleh sebesar 6,3 × 10- 1, yang artinya skewness bernilai positif (kemiringan ekor yang lebih memanjang ke kanan). Sedangkan skewness pada return saham Twitter diperoleh sebesar -4,3 × 10“ 1 , yang artinya skewness bernilai negatif (kemiringan ekor yang lebih memanjang ke kiri). Selain itu, nilai kurtosis dari return saham Facebook dan saham Twitter diperoleh sebesar 8,4 dan 12,03, yang artinya kurtosis pada kedua saham memiliki keruncingan leptokurtik.
Autokorelasi dan Heterokedastik
Untuk mengetahui apakah data return saham Facebook dan saham Twitter memiliki autokorelasi yang signifikan, dapat dilihat menggunakan plot ACF return pada Gambar 2.
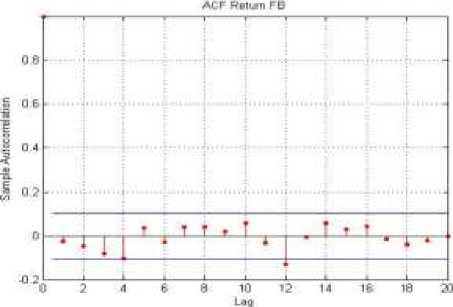
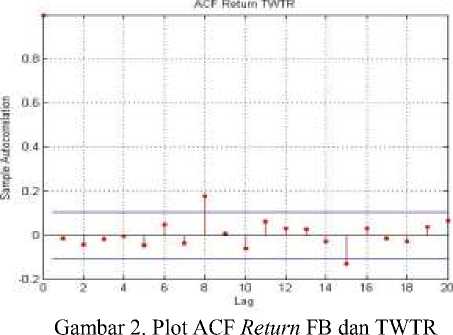
Pada Gambar 2 terlihat sebagian besar lag pada return saham Facebook dan saham Twitter tidak keluar dari batas signifikansi. Hal ini menunjukkan bahwa return saham Facebook dan saham Twitter tidak berautokorelasi. Selain menggunakan plot ACF, ada tidaknya autokorelasi juga dapat dilihat dari hasil uji statistika Ljung-box seperti pada Tabel 2.
Hipotesis uji Ljung-Box return saham Facebook dan Twitter sebagai berikut:
Hq : return saham tidak berautokorelasi.
H^ : return saham berautokorelasi.
Tabel 2. Uji Ljung-Box
|
Saham |
Ljung-Box | ||
|
P-Value |
Qstat |
CV | |
|
FB |
0,5992 |
0,2762 |
3,8415 |
|
0,5584 |
1,1653 |
5,9915 | |
|
0,3076 |
3,6031 |
7,8147 | |
|
0,1049 |
7,6587 |
9,4877 | |
|
0,1550 |
8,0225 |
11,0705 | |
|
TWTR |
0,7727 |
0,0834 |
3,8415 |
|
0,6893 |
0,7443 |
5,9915 | |
|
0,8502 |
0,7971 |
7,8147 | |
|
0,9383 |
0,8015 |
9,4877 | |
|
0,9058 |
1,5617 |
11,0705 | |
Berdasarkan Tabel 2 dapat dilihat untuk setiap nilai P-Value lebih besar dari a = 0,05 dan nilai Qstat lebih kecil daripada nilai CV. Hal ini menunjukkan bahwa tolak Hy atau terima Hq , yang artinya return dari saham Facebook dan saham Twitter tidak berautokorelasi.
Selanjutnya akan diperiksa ada tidaknya efek heteroscedasticity pada return saham Facebook dan saham twitter. Heteroscedasticity dapat dilihat menggunakan plot ACF kuadrat return pada Gambar 3 dan Gambar 4.
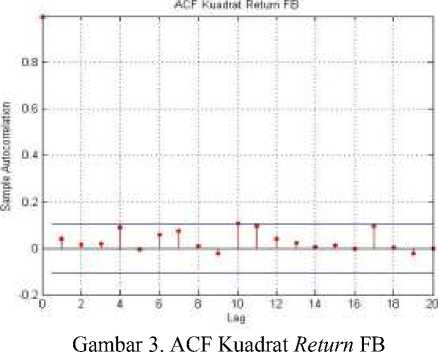
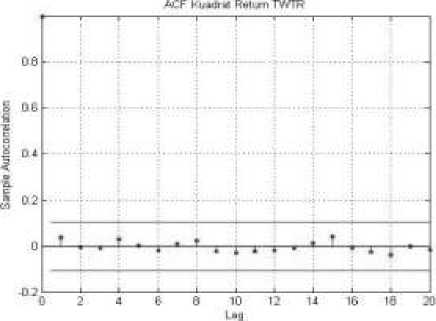
Gambar 4. ACF Kuadrat Return TWTR
Pada Gambar 3 dan Gambar 4 menunjukkan semua lag pada data kuadrat return saham Facebook maupun saham Twitter tidak keluar dari batas. Hal ini mengindikasi tidak adanya sifat heteroscedasticity pada data. Untuk memperjelas ada tidaknya efek
heteroscedasticity, dapat dilihat dari hasil uji ARCH LM seperti pada Tabel 3.
Hipotesis uji ARCH LM return saham Facebook dan Twitter sebagai berikut:
Hq : homoscedasticity, tidak ada efek ARCH pada return saham.
Hy : heteroscedasticity, terdapat efek ARCH pada return saham.
Tabel 3. Uji ARCH LM
|
Saham |
ARCH LM | ||
|
P-Value |
Qstat |
CV | |
|
FB |
0,5073 |
0,4397 |
3,8415 |
|
0,7811 |
0,4940 |
5,9915 | |
|
0,9002 |
0,5837 |
7,8147 | |
|
0,6247 |
2,6122 |
9,4877 | |
|
0,7442 |
2,7127 |
11,0705 | |
|
TWTR |
0,4689 |
0,5245 |
3,8415 |
|
0,7604 |
0,5478 |
5,9915 | |
|
0,9090 |
0,5445 |
7,8147 | |
|
0,9394 |
0,7926 |
9,4877 | |
|
0,9779 |
0,7859 |
11,0705 | |
Berdasarkan Tabel 3 dapat dilihat untuk setiap nilai P-Value lebih besar dari a = 0,05 dan nilai Qstat lebih kecil daripada nilai CV. Hal ini menunjukkan bahwa tolak H1 atau terima H0, yang artinya return saham Facebook dan saham Twitter bersifat homoscedasticity, tidak ada efek ARCH pada return masing-masing saham.
Pareto tail
Pada data finansial sering kali terjadi kasus ekor gemuk (heavy tail) yang mengindikasi adanya nilai ekstrem. Untuk melihat adanya indikasi nilai ekstrem tersebut dapat digunakan plot Pareto tail seperti pada Gambar 5.
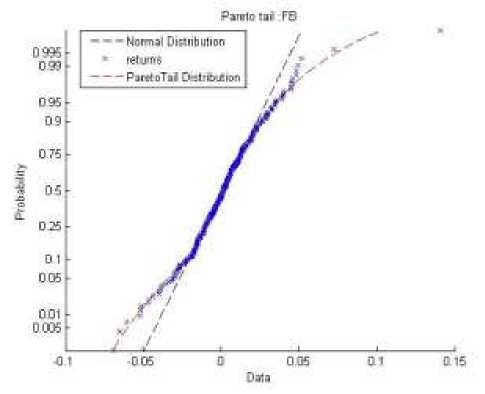
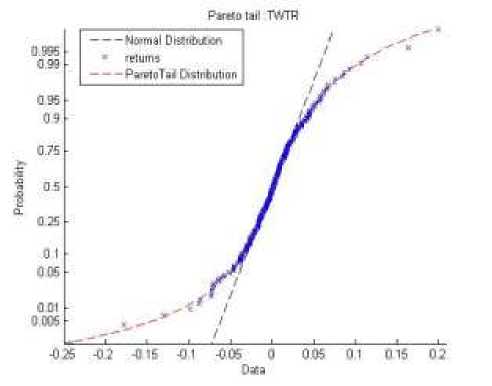
Gambar 5 Plot Pareto Tail FB dan TWTR
Pada Gambar 5 terlihat adanya indikasi nilai ekstrem pada return saham Facebook dan saham Twitter. Nilai ekstrem tersebut dapat dilihat pada ekor Pareto bagian bawah maupun ekor Pareto bagian atas pada masing-masing saham. Adanya nilai ekstrem tersebut, mempengaruhi tingkat risiko yang mungkin ditanggung ke depannya. Dengan kata lain, semakin banyak data yang mengumpul pada ekor Pareto akan menyebabkan tingkat risiko yang ditanggung juga semakin besar.
Estimasi Parameter Gaussian Copula
Pada tahap ini akan dilakukan estimasi parameter Gaussian copula. Adapun
parameternya adalah rho (p). Pada tahap ini akan digunakan Kendall’s tau yang dianggap cocok pada kasus bivariat. Sebelum mengestimasi parameter, hal yang harus dilakukan terlebih dahulu adalah mencari nilai tau (r) dari saham Facebook dan saham Twitter. Selanjutnya dari nilai τ yang telah diperoleh tersebut, digunakan untuk mengestimasi parameter Gaussian copula. Dengan
menggunakan software MATLAB 2013
diperoleh parameter Gaussian copula sebagai berikut:
1 0,5941
P = [ 0,594 1 J'
Dari hasil estimasi parameter, diperoleh koefisien korelasi dari saham Facebook dan saham Twitter sebesar 0,594. Nilai koefisien korelasi tersebut menunjukkan bahwa saham
Facebook dan saham Twitter berkorelasi positif sempurna, yang artinya kedua saham dalam portofolio bergerak searah.
Simulasi Gaussian Copula
Pada tahap ini dilakukan simulasi data dengan membangkitkan sejumlah bilangan acak berbasis Gaussian copula menggunakan parameter yang telah diperoleh sebelumnya. Simulasi dapat dilakukan sebanyak n kali (sejumlah yang diinginkan). Pada penelitian ini digunakan simulasi sejumlah n = 1000. Setelah memperoleh hasil simulasi data return, selanjutnya ditentukan bobot (proporsi) dana yang ingin diinvestasikan guna memperoleh return portofolio. Bobot yang digunakan sebesar 0,5 pada masing-masing saham. Selanjutnya dihitung nilai VaR portofolio menggunakan fungsi Gaussian copula sebesar tingkat kepercayaan yang telah ditentukan. Setelah memperoleh nilai VaR, kemudian dihitung estimasi nilai CVaR sebesar tingkat kepercayaan yang telah ditentukan. Pada penelitian ini digunakan tingkat kepercayaan sebesar 90%, 95%, dan 99%.
Menghitung Nilai VaR Menggunakan Fungsi Gaussian Copula
Pada tahap ini akan dihitung nilai VaR dari return saham Facebook dan saham Twitter menggunakan fungsi Gaussian Copula. Tingkat kepercayaan yang digunakan pada penelitian ini yaitu 90%, 95%, dan 99%. Nilai VaR dari return saham Facebook dan saham Twitter dapat dilihat pada Tabel 4.
Tabel 4. Nilai VaR
|
Tingkat Kepercayaan | |||
|
90% |
95% |
99% | |
|
VaR |
2,7% |
3,86% |
7,6% |
Pada Tabel 4 diperoleh nilai VaR pada tingkat kepercayaan 90% sebesar 2,7% atau sebesar 0,027. Sedangkan pada tingkat kepercayaan 95% diperoleh nilai VaR sebesar 3,86% atau sebesar 0,0386, dan pada tingkat kepercayaan 99% diperoleh nilai VaR sebesar 7,6% atau sebesar 0,076. Hasil yang diperoleh
tersebut menunjukkan kerugian yang mungkin dialami untuk satu hari ke depan.
Estimasi Nilai CVaR Menggunakan Fungsi Gaussian Copula
Pada tahap ini akan diestimasi nilai CVaR menggunakan fungsi Gaussian copula pada tingkat kepercayaan 90%, 95%, dan 99%. Hasil estimasi dapat dilihat pada Tabel 5.
Tabel 5. Estimasi Nilai CVaR
|
Tingkat Kepercayaan | |||
|
90% |
95% |
99% | |
|
CVaR |
4,7% |
6,1% |
10,6% |
Interpretasi Hasil
Hasil perhitungan estimasi nilai CVaR dapat dilihat pada Tabel 5. Pada tingkat kepercayaan 90% diperoleh nilai CVaR sebesar 4,7% atau sebesar 0,047. Hal ini berarti pada tingkat kepercayaan 90% menunjukkan besarnya risiko kerugian yang mungkin dialami pada satu hari ke depan sebesar 4,7% dari aset saat ini. Sedangkan pada tingkat kepercayaan 95% diperoleh nilai CVaR sebesar 6,1% atau sebesar 0,061. Hal ini berarti pada tingkat kepercayaan 95% menunjukkan besarnya risiko kerugian yang mungkin dialami pada satu hari ke depan sebesar 6,1% dari aset saat ini. Pada tingkat kepercayaan 99% diperoleh nilai CVaR sebesar 10,6% atau sebesar 0,106. Hal ini berarti pada tingkat kepercayaan 99% menunjukkan besarnya risiko kerugian yang mungkin dialami pada satu hari ke depan sebesar 10,6% dari aset saat ini.
Misalnya dengan memiliki modal sebesar $1000.000, maka kerugian yang mungkin dialami pada satu hari ke depan dengan tingkat kepercayaan 90% yaitu sebesar $47.000. Sedangkan pada tingkat kepercayaan 95% kerugian yang mungkin dialami pada satu hari ke depan yaitu sebesar $61.000, dan pada tingkat kepercayaan 99% kerugian yang mungkin dialami pada satu hari ke depan yaitu sebesar $106.000.
Berdasarkan perhitungan dan pembahasan yang telah diuraikan pada bab sebelumnya, diperoleh kesimpulan bahwa estimasi nilai CVaR portofolio yang terdiri dari saham Facebook dan saham Twitter menggunakan fungsi Gaussian copula pada tingkat kepercayaan 90% yaitu sebesar 4,7%. Sedangkan pada tingkat kepercayaan 95% diperoleh sebesar 6,1%, dan pada tingkat kepercayaan 99% diperoleh sebesar 10,6%. Hasil yang diperoleh tersebut menunjukkan kerugian yang mungkin dialami untuk satu hari ke depan.
Adapun saran yang diberikan yaitu penelitian ini dapat dikembangkan menggunakan fungsi Archimedian copula. Adapun anggota keluarga dari Archimedian copula yang dapat digunakan yaitu Clayton copula, Frank copula, dan Gumbel copula.
DAFTAR PUSTAKA
-
[1] Artzner, P., Delbaen, F., Eber, J-M., Heath, D. 1999. Coherent Measures of Risk. Mathematical Finance, Vol. 9, No. 3, pp 203-228.
-
[2] Embrechts, P., McNeil, A., and Straumann, D. 2001. Correlation and Dependence in Risk Management: Properties and Pitfalls, In Risk Management: Value at Risk and Beyond, ed. by M. Dempster and H. K. Moffatt, Cambridge University Press.
-
[3] Franke, J., Härdle, W. K., & Hafner, C. M. 2008. Statistics of Financial Markets: An Introduction (second edition ed.). Berlin: Springer.
-
[5] Letmark, M. 2010. Robustness of Conditional Value-at-Risk (CVaR) When Measuring Market Risk Across Different Assets Classes. M.S. Thesis. Royal Institute of Tekhnology. Swedia.
-
[6] Rockafellar, R.T., Uryasev, S. 2000. Optimization of Conditional Value-at-Risk. Journal of Risk, Vol. 2, No. 3, pp 21-41.
-
[7] Sunaryo, T. 2007. Manajemen Risiko Finansial. Jakarta: Salemba Empat.
194
Discussion and feedback