E-Jurnal Matematika Vol. 4 (4), November 2015, pp. 152-157

ISSN: 2303-1751

MENENTUKAN FORMULA PREMI TAHUNAN TIDAK KONSTAN PADA ASURANSI JOINT LIFE

I Gede Bagus Pasek Subadra§1, I Nyoman Widana2, Desak Putu Eka Nilakusmawati3

ABSTRACT

The aim of this research was to determine the annual premium formula that turns on the joint life insurance. This formula uses the reference insurance contracts of the previous research Insurance Models for Joint Life and Last Survivor Benefits. The first step is to determine the value of mortality tables by using the Table Helligman-pollard. Furthermore, determining the value of a life annuity and single premium. The results of this research was formula to be affected by the changing premium (a) with the increase and decrease in constant interest.

Keywords: The Annual Premium, The Annual Premium Turned, Joint Life Insurance, α.

  • 1.    PENDAHULUAN

Pada kebutuhan hidup berkeluarga tentunya sebagai seorang kepala keluarga ingin sekali berusaha untuk menjamin kesejahteraan keluarganya. Kesejahteraan tersebut akan terganggu apabila kepala keluarga jatuh sakit, cacat ataupun meninggal dunia. Sebagian dari jaminan kesejahteraan dapat diperoleh apabila kepala keluarga mengasuransikan dirinya agar kesejahteraan hidup keluarga dapat terpenuhi (Sembiring [5]). Kesejahteraan tersebut dapat terpenuhi apabila kepala keluarga tersebut mengikuti asuransi. Sampai saat ini ada berbagai jenis kontrak asuransi, yaitu asuransi individu atau asuransi untuk satu orang dan asuransi bersama atau asuransi minimal dua orang.

Asuransi jiwa merupakan salah satu instrumen yang dapat digunakan untuk memindahkan resiko, dimana apabila terjadi resiko kematian pada seseorang maka ahli warisnya akan memperoleh sejumlah dana yang disebut uang pertanggungan atau santunan. Sebagai konsekuensinya peserta asuransi diwajibkan untuk membayar sejumlah uang

kepada perusahaan asuransi jiwa setiap jangka waktu tertentu, yang biasa disebut premi.

Perusahaan asuransi jiwa merupakan perusahaan yang memberikan jasa dalam penanggulangan risiko yang dikaitkan dengan hidup atau meninggalnya seseorang yang dipertanggungkan. Suatu perusahaan asuransi jiwa tidak menutup kemungkinan untuk menawarkan produk asuransi kepada peserta yang ingin melakukan asuransi jiwa secara bersama atau asuransi joint life. Asuransi joint life adalah suatu keadaan di mana aturan hidup dan matinya merupakan gabungan dari dua faktor atau lebih, misalnya suami-istri, orangtua-anak, suami-istri-anak, dan lain sebagainya (Futami [3]). Peserta yang mengikuti asuransi joint life wajib membayar suatu kewajiban (premi) setiap tahunnya sesuai dengan kontrak.

Dilihat dari besarnya pembayaran premi, ada dua jenis pembayaran premi, yaitu pembayaran premi standar/konstan dan pembayaran premi yang berubah atau premi tidak konstan. Untuk pembayaran premi standar/konstan setiap tahun besar pembayarannya selalu sama sedangkan jika setiap tahun besar pembayaran preminya berubah maka disebut asuransi dengan 152

pembayaran premi yang berubah atau premi tidak konstan. Hal ini juga perlu dilakukan mengingat besarnya penghasilan masyarakat tidak selalu tetap.

Pada penelitian ini akan dilakukan bagaimana menentukan formula premi tahunan tidak konstan pada asuransi joint life.

  • 2.    METODE PENELITIAN

Pada penelitian ini digunakan kontrak asuransi yang terdiri dari pasangan suami-istri, apabila peserta berusia x tahun dan y tahun tetap hidup mencapai kontrak asuransi berakhir atau dengan kata lain peserta mencapai usia X+n dan y+n, maka peserta mendapatkan uang pertanggungan sebesar Q. Apabila salah satu dari peserta meninggal dunia sebelum masa kontrak misalnya apabila y meninggal dunia sebelum masa kontrak berakhir maka x mulai tahun ke-n selama seumur hidup setiap tahunnya mendapatkan uang pertanggungan (benefit) sebesar Rx , demikian juga sebaliknya apabila x meninggal dunia maka y akan mendapat uang pertanggungan (benefit) sebesar Ry . Apabila kematian dari pasangan juga terjadi (x dan y meninggal) sebelum kontrak berakhir maka ahli waris akan mendapatkan uang pertanggungan sejumlah premi yang telah dibayarkan, pada akhir tahun kematiannya (Futami [2]).

Perbandingan antara peluang meninggalnya peserta x tahun sebelum mencapai usia x+1 tahun dengan peluang peserta x tahun tetap bertahan hidup selama 1 tahun (Matvejevs & Matvejevs [4]) dapat dirumuskan sebagai

— = (X + B) +D× exp{-E×(lnx-lnF)2}+G× Hx. Px

dengan A,B,C,D,E,F,G,H merupakan nilai kostanta dari Tabel 2.1.

Peluang orang berusia x tahun akan tetap hidup selama n tahun dan y tahun akan tetap hidup selama n tahun dinotasikan dengan nPxy (Futami, [3]) dirumuskan sebagai

nPxy = × nPy .

Anuitas yang pembayarannya dijanjikan akan dilakukan selang beberapa waktu kemudian disebut anuitas tunda. Anuitas yang ditunda

pembayarannya ada yang dilakukan di awal tahun (Futami [2]) dapat dirumuskan sebagai

Tabel 2.1. Nilai Konstan dari Formula

Helligman-Pollard

Konstan

Pria

Wanita

A

0.00194

0.00115

B

0.05093

0.03310

C

0.14249

0.12811

D

0.00607

0.00029

E

1.61992

23.44606

F

57.83349

21.11713

G

0.00005

0.00006

H

1.10715

1.09116

Sumber: (Matvejevs & Matvejevs [4]).

Nilai sekarang anuitas awal dari anuitas hidup berjangka joint life apabila x dan y tetap hidup (Matvejevs & Matvejevs [4]) dirumuskan sebagai

̈ xy : ⌉=1+V. Pxy + V2 . 2pxy+⋯+vn~1. n-lPxy.

Besar premi ditentukan dengan prinsip ekuivalensi dan mempunyai persamaan

E(L)=0.

dengan L menyatakan besarnya kerugian pihak penanggung yang didefinisikan sebagai variabel random dari nilai tunai benefit yang dibayarkan pihak penanggung.

Premi tunggal adalah pembayaran premi asuransi yang dilakukan pada waktu kontrak asuransi disetujui, selanjutnya tidak ada pembayaran lagi. Premi tunggal pure endowment adalah pembayaran premi pada suatu kontrak asuransi jiwa yang dibayarkan pemegang polis, mulai dari saat kontrak dimulai sampai dengan jangka waktu tertentu (Eric V. Slud [1]). Premi tunggal pure endowment joint life untuk peserta yang berusia x tahun dan y tahun, dengan jangka waktu tertanggung n tahun (Futami [3]) dirumuskan sebagai

^xy: ̅̅̅|= V nPxy .

Asuransi berjangka adalah suatu asuransi apabila pemegang polis mulai disetujuinya kontrak asuransi sampai dengan jangka waktu tertentu (meninggal) sebelum masa kontrak selesai maka akan dibayarkan uang

pertanggungannya (Matvejevs & Matvejevs [4]). Premi tunggal asuransi berjangka joint life dirumuskan sebagai

n

Axy: n⌉=∑Vt ( tPxy - t+lpxy). t=l

Usia tertanggung x tahun dan y tahun, meninggal pada tahun polis pertama besarnya uang pertanggungan dikalikan 1, meninggal tahun polis kedua besarnya uang pertanggungan dikalikan 2, dan seterusnya. Setiap tahun apabila meninggal besarnya uang pertanggungan selalu bertambah 1. Asuransi yang demikian ini disebut juga asuransi berjangka menaik. Untuk masa pertanggungan selama n tahun, uang pertanggungan dibayarkan pada akhir masa pertanggungan, single preminya dinotasikan dengan (IA ) χy :n⌉ (Futami [3]) dan dirumuskan sebagai n

( IA ) xy : n⌉=∑t Vt ( tpxy - t+lpxy). t=l

Sehubungan dengan asuransi tersebut maka nilai tunai dari pendapatan premi dan nilai tunai dari benefit yang dibayarkan oleh pihak penanggung dapat (Matvejevs & Matvejevs [4]) dirumuskan sebagai

  • 1.    Nilai tunai dari pendapatan premi tahunan konstan pada joint life dapat dinyatakan sebagai

p.(1+V. Pxy+⋯+Vn l. n-lpxy).     (2.1)

  • 2.    Nilai tunai dari benefit yang dibayarkan oleh pihak penanggung dapat dinyatakan sebagai n-l ∞

  • O. Vn . npxy + Px^∑∑ ' ^mI Qy m=0 k=n n-l ∞

+ Ry∑∑Vmmpy kI Qx +p.(IA ) xy : n⌉ k=0 m=n

= Q. Axy:n| +Rx .nI a' x. nQy + Ry .nI a' y. nQx

+p.(IA ) xy : n⌉.                              (2.2)

  • 3.    Dengan menggunakan prinsip ekuivalensi, besar preminya adalah

p.a■ xy : n⌉=Q. Axy:n| +RX .n|̈x. TiQy

+ Ry .n|̈y. TlQx +p.(IA ) xy : ⌉.

Sehingga besarnya premi tahunan yang harus dibayarkan oleh peserta asuransi adalah

P

Axy:̅̅̅|+Rx.n|̈ . TiQy + Ry .n|̈y. TlQx ̈ ,xy: ⌉-(IA ) xy : ⌉

.(2.3)


  • 3.    HASIL PENELITIAN DAN DISKUSI

    • 3.1    Premi Konstan

Nilai premi tahunan konstan pada asuransi joint life sudah dicari dengan menggunakan rumus persamaan (2.3). dengan menggunakan

X=50 tahun,y=45 tahun,Rx =   =  =1 dan

n=10taℎun

Sehingga diperoleh

P = 0.347525802.

  • 3.2    Formula Premi Tahunan Tidak Konstan

Kontrak asuransi melibatkan pasangan suami-istri dengan usia berturut-turut x tahun dan y tahun. Pembayaran premi dilakukan n tahun selama keduanya masih hidup. Besarnya pembayaran premi selalu berubah setiap tahunnya tergantung tingkat bunga menurun atau menaik yang digunakan (a). Misalkan P pembayaran yang dilakukan di tahun pertama, P+a merupakan pembayaran di tahun kedua, dan seterusnya sampai tahun ke-n yang pembayarannya adalah P+(n-1)a.

Rincian dari uang pertanggungan (benefit) adalah

  • 1.    Setelah n tahun apabila kedua peserta (x dan y)  masih tetap hidup mereka akan

mendapatkan uang pertanggungan sebesar Q rupiah. Dengan demikian kontrak asuransi ini berakhir.

  • 2.    Jika salah satu dari pasangan ini meninggal dunia, misalkan y meninggal dunia, maka ada dua kemungkinan untuk pembayaran benefitnya, yaitu :

  • a. Di akhir tahun dari kematian pasangannya (di awal tahun berikutnya) dengan benefit sejumlah premi yang dibayarkan atau dengan kata lain semua 154

    premi yang telah dibayarkan akan dikembalikan.

    b. Setelah berakhirnya masa pembayaran premi yaitu setelah pasangannya mencapai usia X+n tahun. Maka setiap tahunnya peserta x memperoleh uang pertanggungannya sebesar Rx rupiah selama seumur hidup (selama x masih tetap hidup) demikian juga sebaliknya jika peserta x yang meninggal dunia maka peserta y akan memperoleh sebesar Ry rupiah.

    3. Jika pasangan yang keduanya meninggal dunia sebelum kontrak selesai dengan kata lain x dan y meninggal maka kontrak berakhir dan tidak ada lagi pembayaran.

    Sehubungan dengan kontrak asuransi tersebut maka nilai tunai dari pendapatan premi dan nilai tunai dari benefit yang dibayarkan oleh pihak penanggung dapat dirumuskan sebagai

    1. Nilai tunai dari pendapatan premi tahunan tidak konstan pada joint life dapat dinyatakan sebagai

    (p+⋯+(p+(n-1)a) vn 1 ∙ n—lPxy)


    + Ry∑∑Vm ∙ mPx kQx


    +ιp ∙∑t vt (t-lPxy \ t=1


    +∑(ta )    ( tPxy -

    t=0


    -


    ))


    lPxy).


    =   ∙ A χy:̅̅̅|+Rx ∙n|̈∙ nQy + Ry ∙n|̈y∙ nQx


    +ιp ∙∑ tvt (t-lPxy

    \ t=1


    -


    ))


    3.


    +∑(ta)    ( tPxy -

    t=0


    lPxy).


    Dengan menggunakan prinsip ekivalensi, besar preminya adalah


    (p∙̈ 'Xy : ⌉)+a∑ t Vt + 1 tPXy

    t=0


    =   ∙ Aχy:̅̅̅|+Rx ∙n|̈∙ nQy + Ry ∙n|̈y∙ nQx


    +ιp ∙∑tvt (t-lPxy

    \ t=1


    -


    ))


    +a


    t=0’


    ∙ +        .

    t xy


    2. Nilai tunai dari pengembalian premi yang dibayarkan oleh pihak penanggung dinyatakan sebagai


    Dengan demikian dapat ditentukan formula premi tahunan tidak konstan yang harus dibayarkan peserta asuransi joint life, yaitu:

    1


    =   ∙∑tvt (t-lPxy


    -


    ))


    =

    ̈ xy : ⌉


    -.∑"=1 tvt (t-lPxy - tPxy)/


    n-1

    +∑(ta ) vt÷1 ( tPxy - t+lPxy).

    t=0


    ∙[∙ Aχy:̅̅̅| + Rx ∙n|̈X∙ nQy + Ry ∙n|̈


    ∙ TiQx+∑(ta )    ( tPxy - t+

    t=0


    Sehingga nilai tunai yang diharapkan dari benefit yang dibayarkan oleh pihak penanggung adalah


    -


    n-1              -i

    a ∑(t) Vt tPXy]. t=o            J


    Q∙ Vn nPxy + Rx∑∑Vk

    m=0 k=n


    kPx mQy


    Berikut diberikan contoh perhitungan (ilustrasi kasus) perhitungan premi tahunan tidak konstan.

    1. Usia mulai asuransi

    Usia mulai asuransi adalah usia yang ditetapkan sebagai mulainya peserta (suami-istri) mengikuti asuransi. Dalam kasus ini,


usia suami (x) adalah 50 tahun dan usia istri (y) adalah 45 tahun.

  • 2.    Masa pertanggungan asuransi

Masa pertanggungan asuransi adalah lamanya peserta melakukan kontrak asuransi. Dalam kasus ini, ditetapkan untuk masa pertanggungan asuransi n=10 tahun.

  • 3.    Tingkat bunga

Besarnya tingkat bunga yang digunakan adalah konstan yaitu i=5%.

  • 4.    Santunan

Besarnya santunan setelah masa pertanggungan berakhir apabila kedua peserta masih hidup, maka mereka akan diberikan uang sejumlah 1 rupiah (Q =1 rupiah) demikian juga apabila (y) meninggal dan (x) tetap hidup diakhir kontrak, maka (x) akan memperoleh 1 rupiah (Rx=1 rupiah) setiap tahunnya selama seumur hidup. Hal yang sama juga berlaku apabila (x) meninggal dan (y) tetap hidup, maka akan dibayar sebesar 1 rupiah ( Ry=1 rupiah). Tetapi apabila (x) dan (y) meninggal dunia sebelum kontrak berakhir, maka semua pembayaran premi yang telah dibayarkan akan dikembalikan.

Berdasarkan rumus yang diperoleh, besarnya pembayaran premi tahunan tidak konstan sangat dipengaruhi oleh besarnya nilai a yang digunakan. Misalkan a dipilih bernilai negatif maka ini berarti besar pembayaran preminya selalu menurun setiap tahun. Demikian pula sebaliknya jika a dipilih bernilai positif maka preminya selalu meningkat sebesar a setiap tahun. Pada penelitian ini mula-mula besarnya nilai a yang digunakan adalah 10% dari premi konstan atau dengan kata lain premi menurun sebesar a = -0.03475 dan premi meningkat sebesar a = 0.03475. Sedangkan konstanta- konstanta yang lain nilainya sama dengan konstanta pada perhitungan premi konstan.

Jika a = -0.03475, diperoleh besar premi tahun pertamanya adalah

Pi = 0.469136808.

Akibatnya besar premi pada tahun ke-t untuk t=1,2,3,…10 adalah

Pt=0.469136808-0.03475(t-1).

Sedangkan jika a = 0.03475 besar premi tahun pertamanya adalah

Pi = 0.225914796.

Dan premi pada pada tahun ke-t adalah

Pt=0.225914796+0.03475(t-1).

Setelah mendapatkan hasil dari premi tahunan tidak konstan maka dapat dibandingkan hasilnya dengan premi tahunan konstan, dapat dilihat pada Tabel 3.1.

Tabel 3.1. Premi Kostan dan Premi Tidak

Konstan

Tahun

Premi Konstan

Premi menurun

Premi meningkat

1

0.34753

0.46914

0.22592

2

0.34753

0.43439

0.26067

3

0.34753

0.39964

0.29542

4

0.34753

0.36489

0.33017

5

0.34753

0.33014

0.36492

6

0.34753

0.29539

0.39967

7

0.34753

0.26064

0.43442

8

0.34753

0.22589

0.46917

9

0.34753

0.19114

0.50392

10

0.34753

0.15639

0.53867

Jumlah Premi

3.4753

3.12765

3.82295

Perbandingan antara premi a menurun dengan premi a meningkat terlihat pada Tabel 3.1.

Pada pembayaran tahun pertama premi a menurun dengan premi a meningkat adalah 2 : 1 dan setelah pembayaran di akhir tahun terlihat bahwa perbandingannya adalah 1 : 3. Tetapi untuk besarnya uang pertanggungan yang didapatkan jauh berbeda antara premi a menurun dengan a meningkat. Pada premi a menurun sebesar 3.12765 sedangkan premi a meningkat sebesar 3.82295.

Apabila Tabel 3.1 disajikan dalam bentuk grafik, untuk pembayaran premi konstan dan premi yang menurun disajikan pada Gambar 3.1.


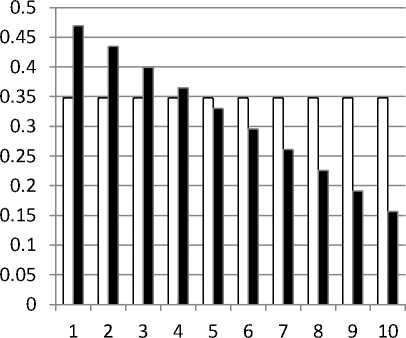
Gambar 3.1. Premi Konstan dan Premi Menurun

Sedangkan grafik untuk premi konstan dan premi meningkat dapat dilihat pada Gambar 3.2.

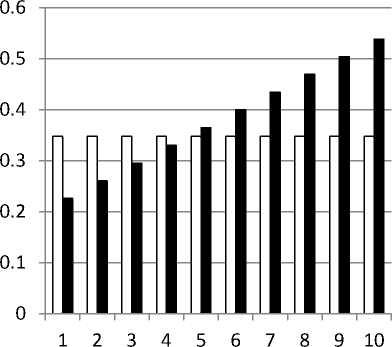
Gambar 3.2 Premi Konstan dan Premi Meningkat

Untuk pembayaran premi yang menurun (PT) , dari Gambar 3.1 terlihat bahwa

PT tahun ke-10 < PK < PT tahun ke-1

Selain itu, perlu dicatat bahwa mulai di tahun ke-5 peserta asuransi joint life akan membayar premi yang lebih kecil daripada peserta dengan model pembayaran premi konstan. Hal yang sebaliknya berlaku untuk pembayaran premi yang selalu meningkat.

PN tahun ke-1<PK < PN tahun ke-10 dan ditahun ke-5 peserta asuransi joint life ini akan membayar premi yang lebih besar daripada dengan model pembayaran premi konstan.

4. KESIMPULAN DAN SARAN


Berdasarkan pembahasan dan hasil

penelitian yang diperoleh, maka dapat

disimpulkan, bahwa:


Rumusan/formula penentuan premi tahunan

tidak konstan pada asuransi joint life adalah

p =


1

a ' xy : n⌉-(IA ) xy n⌉

[Q∙Aχy:^ + Rx ∙ xy:n\     x


n\ax∙ nQy


n-1

+ Ry ∙n\ay∙ nQx +a ∑(t) N^ ( tPxy - t+iPxy) t=i

n-i

-a∑(t) Vt tPxy] t=l

untuk masa pertanggungan n tahun.

Beberapa saran untuk penelitian selanjutnya, yaitu: (1) Peneliti dapat melanjutkan penelitian tentang bagaimana menentukan formula premi tahunan pada asuransi joint life untuk tertanggung lebih dari 2 orang dan (2) Peneliti dapat juga melanjutkan penelitian dalam menentukan formula dari cadangan premi pada asuransi joint life.

DAFTAR PUSTAKA

  • [1]    Eric V. Slud, 2001. Actuarial Mathematics. College Park.

  • [2]    Futami, T., 1993. Matematika Asuransi

Jiwa Bagian I. Tokyo: Oriental Life Insurance Cultural Development Center.

  • [3]   _________. 1994. Matematika Asuransi

Jiwa Bagian II. Tokyo: Oriental Life Insurance Cultural Development Center

  • [4]    Matvejevs, A. & Matvejevs, A., 2001.

Insurance Models for Joint Life and Last Survivor Benefit, Informatica, 12(4), pp. 547-58.

  • [5]    Sembiring, R.K., 1986. Asuransi I. Jakarta: Universitas Terbuka, Depdikbud.

157