E-Jurnal Matematika Vol. 4 (3), Agustus 2015, pp. 122-126

ISSN: 2303-1751

IMPLEMENTASI METODE MARKOV CHAIN MONTE CARLO DALAM PENENTUAN HARGA KONTRAK BERJANGKA KOMODITAS

Putu Amanda Setiawani§1, Komang Dharmawan2, I Wayan Sumarjaya3

1Jurusan Matematika Fakultas MIPA - Universitas Udayana [Email: amandasetiawani7@gmail.com]

§Corresponding Author

ABSTRACT

The aim of the research is to implement Markov Chain Monte Carlo (MCMC) simulation method to price the futures contract of cocoa commodities. The result shows that MCMC is more flexible than Standard Monte Carlo (SMC) simulation method because MCMC method uses hit-and-run sampler algorithm to generate proposal movements that are subsequently accepted or rejected with a probability that depends on the distribution of the target that we want to be achieved. This research shows that MCMC method is suitable to be used to simulate the model of cocoa commodity price movement. The result of this research is a simulation of future contract prices for the next three months and future contract prices that must be paid at the time the contract expires. Pricing future contract by using MCMC method will produce the cheaper contract price if it compares to Standard Monte Carlo simulation.

Keywords: futures contract, Markov Chain Monte Carlo, Standard Monte Carlo, hit-and-run sampler

  • 1.    PENDAHULUAN

Saat ini pasar keuangan mengalami perkembangan yang sangat pesat. Hal ini menyebabkan terjadinya perubahan situasi dan kondisi pasar yang cenderung menimbulkan risiko bagi para investor. Pengurangan risiko pasar dapat dilakukan dengan menggunakan kontrak derivatif seperti halnya kontrak berjangka sebagai instrumen lindung nilai. Hal ini dilakukan untuk menurunkan tingkat varians return dari harga suatu komoditas. Perdagangan dengan menggunakan kontrak berjangka (futures contract) akan membantu harga komoditas yang ada di pasaran menjadi lebih stabil.

Markov Chain Monte Carlo (MCMC) merupakan salah satu metode yang digunakan untuk melakukan pengambilan sampel yang tidak sesuai dengan asumsi dalam sebuah penelitian. Pada penelitian sebelumnya, metode MCMC pernah digunakan oleh Johannes,

Kumar,& Polson [1] dan Eraker, Johannes, & Polson [2] yang membahas tentang kegunaan MCMC sebagai alat dalam penentuan model harga saham. Penelitian oleh Landauskas dan Valakevicius (2011) juga menggunakan metode MCMC untuk memodelkan harga saham. Pendekatan model pada penelitian Landauskas dan Valakevicius dilakukan dengan tujuan untuk menghilangkan semua anggapan atau asumsi dari distribusi harga saham yang ingin dimodelkan (Landauskas & Valakevicius [3]). Metode MCMC merupakan alat analisis data yang dapat digunakan untuk menghasilkan sampel yang tidak saling bebas. Hal ini sesuai dengan sifat data finansial yang merupakan suatu kelompok data tertentu yang terdiri dari urutan kejadian yang saling dependent. Penelitian ini dilakukan dengan tujuan untuk dapat mengimplementasikan metode MCMC dalam menentukan harga kontrak berjangka suatu komoditas.

Penggunaan metode MCMC tersebut selanjutnya dibandingkan dengan metode Standard Monte Carlo untuk mengetahui hasil yang terbaik. Data yang digunakan dalam penelitian ini adalah data historis harga komoditas kakao (International Cocoa Organization) selama 1 Februari 2012 sampai 1 Februari 2015.

Kontrak Berjangka Komoditas

Definisikan harga kontrak pada waktu dan harga komoditas dengan adalah risk free rate dan biaya asuransi komoditas sebesar %. Dalam kondisi ini, nilai dari futures contract adalah

=    (    ) .                            (1)

Model Pergerakan Harga Komoditas

Model pergerakan harga komoditas mengikuti bentuk persamaan model geometric Brownian motion,

(     )      √

=                            (2)

dengan adalah harga komoditas pada saat mendatang , merupakan volatilitas, adalah ekspektasi tingkat pengembalian (return).

Barisan Bilangan Acak

Misalkan {  }   , ,…, menjadi barisan

variabel acak yang independen dan berdistribusi identik diperoleh =∑ dan

Mn =⅛‰ 1 ¾.

Misalkan    menyatakan nilai mean dan

menyatakan nilai varians, dengan demikian didefinisikan sebagai

Zn = √⅛[∑^ ι(¾-¾)]'  (3)

Teorema limit pusat menyatakan bahwa ketika mendekati tak terhingga, variabel acak konvergen pada arah distribusi Gauss dengan nilai rata-rata nol dan varians unit.

Metode Markov Chain Monte Carlo

Markov Chain Monte Carlo (MCMC) adalah metode untuk membangkitkan peubah-peubah acak yang didasarkan pada rantai

Markov. Untuk sebarang titik awal, rantai Markov akan konvergen ke suatu distribusi invarian () (Andrieu, et. al. [4]). Dalam hal ini MCMC adalah metode yang dapat digunakan untuk memenuhi tujuan pengambilan sampel yang diperlukan. Gagasan utamanya adalah untuk membangun rantai Markov {} sehingga

lim→(=)=().        (4)

Langkah-langkah yang dilakukan untuk membangkitkan sampel dalam metode ini menggunakan algoritma hit-and-run sampler (Kroese, et. al. [5]) adalah sebagai berikut: (a) Diberikan kondisi awal       dan t = 1.

  • (b)    Bangkitkan bilangan acak dt menurut distribusi seragam pada unit hypersphere dimensi-n.

  • (c)    Bangkitkan     dari densitas proposal

(proposal  density)    ( |,) yang

memenuhi kondisi keseimbangan sebagai proposal yang layak, sehingga pada iterasi diperoleh

ℳ≝{ ℝ∶+   }

  • (d)    Ambil =+ dan misalkan (,)    ℎ

t+1 Ut untuk yang lainnya dengan (,) merupakan peluang penerimaan (acceptance probability)

()(| ||-(),)

(, ) =min {()(| ||    (),),1}

  • (e)    Jika kriteria konvergensi |-|<10

terpenuhi, maka algoritma selesai. Jika tidak, maka naikkan dan ulangi dari langkah (b).

  • 2.    METODE PENELITIAN

Analisis data dalam penelitian ini dilakukan dengan metode Markov Chain Monte Carlo. Penelitian dilakukan dengan menggunakan bantuan program Matlab 7.8 melalui tahap-tahap sebagai berikut: (1) Menghitung tingkat pengembalian (return) dari harga penutupan (close) komoditas dengan menggunakan bantuan program Matlab; (2) Menghitung nilai statistik deskriptif rata-rata data (mean), ragam data (variance), kepencongan data (skewness), dan kurtosis dari data tingkat pengembalian

harga (return) komoditas; (3) Menghitung nilai parameter yang terdiri dari suku bunga bebas risiko (r), standar deviasi (σ), harga saham awal (Sq), waktu jatuh tempo (n) dan waktu dalam tahun (T) dari data historis harga komoditas; (4) Melakukan simulasi harga komoditas S t menggunakan metode Markov Chain Monte Carlo dengan algoritma hit-and-run sampler; (5) Menghitung nilai rata-rata dari harga komoditas S^ yang diperoleh dari hasil simulasi; (6) Mengestimasi harga kontrak berjangka komoditas Ft dengan menghitung nilai rata-rata dari Ft ; (7) Melakukan simulasi dengan menggunakan metode Standard Monte Carlo; (8) Bandingkan harga kontrak yang diperoleh dari metode Markov Chain Monte Carlo dengan harga kontrak yang diperoleh dari hasil simulasi Standard Monte Carlo.

  • 3.    HASIL DAN PEMBAHASAN

Karakteristik Data Penelitian

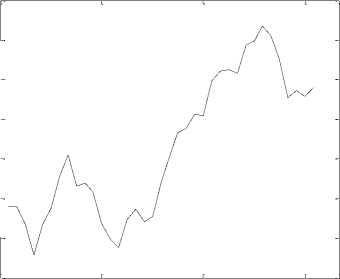
Data historis harga bulanan dari komoditas kakao (International Cocoa Organization) periode 1 Februari 2012 sampai 1 Februari 2015 disajikan dalam bentuk grafik pada Gambar 1.

3400


2000


3200

3000

2800

2600

2400

2200

2012              2013              2014              2015

Waktu (tahun)


Gambar 1. Grafik Harga Komoditas Kakao

Periode 1 Feb 2012 - 1 Feb 2015

Berdasarkan grafik pada Gambar 1 dapat diamati bahwa terjadi fluktuasi harga komoditas kakao pada bulan tertentu. Plot data historis harga komoditas kakao (International Cocoa Organization, 20122015) selama tiga tahun terakhir terlihat juga memiliki tren harga yang cenderung naik.

Karakteristik data dapat diketahui dengan melihat nilai statistik deskriptif dari data tingkat pengembalian harga komoditas kakao. Nilai statistik deskriptif dalam proses ini diperoleh dengan menghitung nilai mean, variance, skewness, dan kurtosis menggunakan bantuan perintah program Matlab, sehingga diperoleh hasil yang dapat dilihat pada Tabel 1.

Tabel 1. Nilai Statistik Deskriptif Data

Karakteristik

Nilai

Mean

0,0072

Variance

0,0016

Skewness

-0,1192

Kurtosis

2,2365

Tabel 1 menunjukkan bahwa model data return harga komoditas ini memiliki bentuk yang tidak simetris. Hal ini ditunjukkan dengan karakteristik data yang memiliki nilai skewness negatif yang mengakibatkan data mencong (skew) ke kiri. Nilai kurtosis yang diperoleh lebih kecil apabila dibandingkan dengan nilai kurtosis yang berdistribusi normal yaitu sebesar 3, maka model ini juga dapat dikatakan memiliki nilai kurtosis yang tidak normal.

Parameter-parameter dari metode MCMC ditentukan dengan menggunakan nilai yang telah didapat pada Tabel 1. Perhitungan nilai-nilai dari parameter (r,c,σ, Sq ,n,T) dapat ditulis sebagai berikut :

  • a.    Tingkat suku bunga (r) pada Februari 2015 sebesar 7,75% (BI,2015).

  • b.    Beban biaya gudang dan asuransi (c ) yang harus ditanggung sebesar 6% per-tahun (Bappepti,2015).

  • c.    Hasil perhitungan nilai volatilitas (σ) dapat ditunjukkan sebagai berikut:

σ=√Variance = √0.0016 = 0,0403.

Nilai volatilitas yang diperoleh dalam tahun adalah sebesar 0,4836.

  • d.    Nilai Sq pada tanggal 1 Februari 2015 sebesar 2961,94 US$/metric tonne.

  • e.    Penelitian ini mengamati perubahan harga komoditas harian sebanyak 66 amatan.

  • f.    Perhitungan waktu jatuh tempo yang

diperlukan dalam penelitian ini adalah

n



256


= 0,257.


Implementasi Metode MCMC

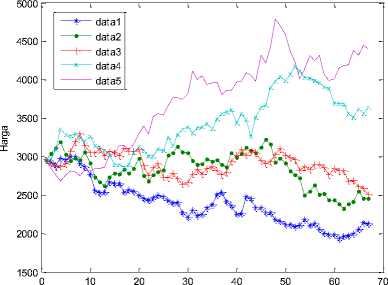
Metode Markov Chain Monte Carlo (MCMC) akan mengikutsertakan pembangkitan bilangan acak dan penggunaan algoritma hit-and-run sampler yang diperlukan untuk melakukan pengulangan (repetisi). Simulasi ini diproses melalui banyak iterasi dengan variabel acak yang berbeda untuk mengestimasi nilai harga komoditas kakao yang akan datang dengan merata-ratakan hasil simulasi yang diperoleh. Simulasi dilakukan dengan memasukkan nilai-nilai dari parameter MCMC ke dalam program Matlab. Hasil simulasi sebanyak lima kali disajikan dalam bentuk grafik pada Gambar 2.

Waktu (hari)

Gambar 2. Grafik Harga (S^) Sebanyak Lima Kali Simulasi Selama Tiga Bulan

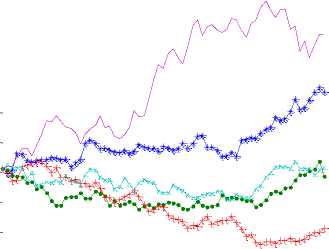
Selanjutnya harga kontrak berjangka komoditas kakao Ft akan dicari menggunakan harga komoditas kakao S^ yang telah didapatkan melalui simulasi sebelumnya. Nilai S t yang didapat akan disubstitusikan pada persamaan (2), sehinggga akan diperoleh harga Ft pada Gambar 3. Rata-rata dari seluruh nilai akhir Ft merupakan nilai harga kontrak yang dicari.

6000

data1

data2

—t— data3 data4 data5

4000

3500

3000

2500

2000

5500

5000

4500

0        10       20       30       40       50       60       70

Waktu (hari)


1500

Gambar 3. Grafik Harga (Ft) Sebanyak Lima Kali Simulasi Selama Tiga Bulan

Selanjutnya, berdasarkan hasil simulasi yang telah dilakukan diperoleh harga kontrak berjangka komoditas kakao yang disajikan dalam bentuk tabel sebagai berikut:

Tabel 2. Harga Kontrak Berjangka

Menggunakan Simulasi MCMC

Jumlah Simulasi (kali)

St         \

Ft

Waktu Simulasi (detik)

5

3058,5

3187,3

0,0040

10

3045,6

3176,3

0,0049

100

3053,6

3139,7

0,0079

1000

3001,9

3126,2

0,0388

10.000

2968,9

3124,6

0,3476

100.000

2967,4

3121,1

3,4667

Tabel 2 memperlihatkan harga kontrak berjangka menggunakan metode MCMC. Tiap simulasi menghasilkan nilai harga kontrak yang berbeda dengan waktu pelaksanaan simulasi yang juga berbeda. Nilai pada tabel menunjukkan bahwa semakin banyak jumlah simulasi yang dilakukan nilai estimasi yang diperoleh akan konvergen ke suatu nilai yang mendekati nilai pada keadaan yang sebenarnya.

Metode Standard Monte Carlo

Harga kontrak berjangka komoditas kakao dihitung menggunakan metode Standard Monte Carlo dengan bantuan program Matlab. Tabel 4.5 memperlihatkan harga komoditas, harga kontrak berjangka, dan waktu simulasi yang disajikan dalam bentuk tabel sebagai berikut:

Tabel 3 Harga Kontrak Berjangka Menggunakan Simulasi Standard Monte Carlo

Jumlah Simulasi (kali)

St       ∖

Ft

Waktu Simulasi (detik)

5

2974,3

3081,7

0,00064

10

3013,9

3122,6

0,00072

100

3004,8

3113,2

0,0023

1000

3017,9

3126,8

0,0170

10.000

3019,8

3128,7

0,1639

100.000

3019,6

3128,6

1,3789

Hasil Perbandingan

Harga kontrak berjangka yang diperoleh dengan menggunakan metode Markov Chain Monte Carlo adalah sebesar 3121,1 US$/metric tonne. Sedangkan harga kontrak berjangka yang diperoleh dengan simulasi Standard Monte Carlo adalah sebesar 3128,6 US$/metric tonne. Nilai varians yang dihasilkan dari metode MCMC sebesar 0,0015 sedangkan nilai varians yang dihasilkan dari metode Standard Monte Carlo sebesar 0,1176. Nilai varians yang lebih kecil dapat menunjukkan hasil simulasi yang lebih baik dan juga memiliki standar penyimpangan data yang lebih kecil. Oleh karena itu dapat ditunjukkan bahwa harga yang dicari dengan menggunakan metode MCMC lebih baik jika dibandingkan dengan harga yang dicari menggunakan simulasi Standard Monte Carlo. Hal ini menunjukkan bahwa pendekatan harga yang menggunakan simulasi Markov Chain Monte Carlo dapat dipakai untuk menentukan harga kontrak berjangka

komoditas kakao dalam periode waktu tiga bulan yang akan datang.

  • 4.    SIMPULAN DAN SARAN

Penelitian ini menunjukkan bahwa metode Markov Chain Monte Carlo (MCMC) menghasilkan harga kontrak berjangka sebesar 3121,1 US$/metric tonne sedangkan simulasi Standard Monte Carlo sebesar 3128,6 US$/metric tonne. Berdasarkan nilai varians yang diperoleh dari kedua metode, dapat ditunjukkan bahwa simulasi MCMC menunjukkan hasil yang lebih baik apabila dibandingkan dengan metode Standard Monte Carlo.

Adapun saran untuk pengembangan penelitian selanjutnya sebaiknya dapat disertakan tingkat suku bunga yang tidak konstan agar dapat menyesuaikan dengan keadaan pasar berjangka yang sebenarnya.

DAFTAR PUSTAKA

  • [1]    Johannes, Kumar, & Polson. 1999. State Dependent Jump Models, How do US Equity Indicies Jump? Working Paper University of Chicago.

  • [2]    Eraker, Johannes, & Polson. 2003. The Impact of Jumps in Volatility and Returns. The Journal of Finance Vol. LVII, No. 3, 1269-1300.

  • [3]    Landauskas, M., & Valakevicius, E. 2011. Modelling of Stock Prices by the Markov Chain Monte Carlo Method. Intellectual Economics, 244-256.

  • [4]    Andrieu, C., de Freitas, N., Doucet, A., & Jordan, M. I. 2003. An Introduction to MCMC for Machine Learning. Machine Learning, 50, 5-43.

  • [5]    Kroese, D. P., Taimre, T., & Botev, Z. I. 2011. Handbook of Monte Carlo Methods. New Jersey: John Wiley & Sons.

126