MODEL NON LINIER GARCH (NGARCH) UNTUK MENGESTIMASI NILAI VALUE at RISK (VaR) PADA IHSG

E-Jurnal Matematika Vol. 4 (2), Mei 2015, pp. 59-66

ISSN: 2303-1751

MODEL NON LINIER GARCH (NGARCH) UNTUK MENGESTIMASI NILAI VALUE at RISK (VaR) PADA IHSG

I Komang Try Bayu Mahendra^§1, Komang Dharmawan², Ni Ketut Tari Tastrawati³

¹Jurusan Matematika Fakultas MIPA – Universitas Udayana [Email: tibey_jr@yahoo.com]

²Jurusan Matematika Fakultas MIPA – Universitas Udayana [Email: dharmawan.komang@gmail.com] ³Jurusan Matematika Fakultas MIPA – Universitas Udayana [Email: taritastrawati@yahoo.com]

^§Corresponding Author

ABSTRACT

In investment, risk measurement is important. One of risk measure is Value at Risk (VaR). There are many methods that can be used to estimate risk based on VaR framework. One of them Non Linier GARCH (NGARCH) model. In this research, determination of VaR used NGARCH model. NGARCH model allowed for asymetric behaviour in the volatility such that “good news” or positive return and “bad news” or negative return. Based on calculations of VaR, the higher of the confidence level and the longer the investment period, the risk was greater. Determination of VaR using NGARCH model was less than GARCH model.

Keywords: GARCH model , NGARCH model, Value at Risk

• 1.    PENDAHULUAN

Pada saat berinvestasi, terdapat dua faktor yang memengaruhi harga saham yaitu tingkat pengembalian saham (return) dan faktor risiko. Faktor risiko digunakan sebagai tolak ukur dalam melakukan investasi agar tidak merugi. Salah satu metode dalam menghitung dan meramalkan risiko adalah Value at Risk (VaR). VaR dapat diartikan sebagai kerugian maksimum yang akan didapat selama periode tertentu dan tingkat kepercayaan tertentu.

Salah satu metode yang bisa digunakan dalam kerangka kerja VaR antara lain model GARCH dan Non linier GARCH (NGARCH). Model GARCH mengasumsikan varian data berubah dalam menghitung variansi atau risiko yang ditanggung pada data indeks saham (Bollerslev [1]). Dalam perkembangannya, terdapat model Non Linier GARCH (NGARCH) yang dikembangkan oleh Engle dan Ng pada tahun 1993 yang merupakan pengembangan dari model GARCH (Brigo et al 2]). Hasil yang diperoleh berbeda-beda setiap waktu karena bersifat asimetris atau

non-linier yang disebut "ekor gemuk". Distribusi ekor gemuk memung-kinkan realisasi variabel acak dengan mengasumsikan nilai-nilai yang lebih ekstrim daripada nilai-nilai yang bersifat normal.

Model NGARCH dapat mengestimasi perilaku volatilitas yang bersifat asimetris atau data saham yang terlalu condong pada suatu titik. Data dalam pengaruh “good news” atau return positif akan menghasilkan volatilitas yang rendah, sedangkan “bad news” atau return negatif akan menghasilkan volatilitas yang lebih tinggi. Penambahan sebuah parameter yang bersifat positif, maka pengaruh terhadap “good news” akan dikurangi dan meningkatkan pengaruh terhadap “bad news” (Brigo et al [2]).

Tingkat Pengembalian (Return)

Return saham adalah keuntungan yang diperoleh dari kepemilikan saham investasi yang dilakukan. Pada analisis sekuritas umumnya menggunakan metode natural logarithm ratio. Hasil dari keuntungan yang diharapkan tidak terlalu besar dibandingkan

metode konvensional. Metode natural logarithm ratio di formulasikan sebagai (Husnan [3]):

R₁ ^,t = ln ( , ^,h)

Penggunaan metode natural logarithm ratio digunakan agar dalam analisis statistika perhitungan return tidak bias.

Nilai Statistik Deskriptif

Nilai statistik deskriptif yang akan dicari dalam proses ini didapat dengan memanfaatkan data penutupan nilai return IHSG. Langkah yang akan dilakukan adalah menghitung nilai rataan, Standar Deviasi, Skewness, dan Kurtosis dari return IHSG menggunakan software Matlab 2009.

Estimasi Parameter dengan MLE

Konsep dasar maximum likelihood estimation (MLE) adalah untuk menemukan estimasi parameter θ dari fungsi densitas peluang fθ dengan memaksimumkan fungsi likelihood.

Dalam melakukan penaksiran melalui MLE akan dicari fungsi densitas peluang bersamanya dari ¾ , X₂,…,^xn yaitu f( X2. , X₂,…,^xn ;θ). Karena ^xI , X₂,…,^xn merupakan sampel acak dari iid maka (Brigo et al [2]),

f(^X1 , *2 ,…,^xn ;θ)=

f(^xI ; 01), f(^X2 ; 02),…,f( ^xn ; θ_n )

Fungsi likelihood ℒ(θ ) yang merupakan fungsi densitas peluang bersamanya dari ^xI , ^X2 , X₃,…,^xn, adalah (Brigo et al [2])

n

ℒ(0)≡fe (^χι , *2 ,… ,^xn)=∏fe (^χi ) i=i

Estimasi MLE ditentukan dengan memaksimalkan fungsi likelihood. Karena nilai fungsi densitas bisa menjadi sangat kecil, maka fungsi likelihood akan diubah menjadi loglikelihood yang dinyatakan sebagai (Brigo et al [2]):

ℒ^∗(θ)=∑logfe (X_i ) i=i

Melihat Autokorelasi Data Melalui ACF dan PACF

Fungsi autokorelasi digunakan untuk mengukur ketergantungan bersama (mutual dependen) antara nilai-nilai suatu runtun waktu yang sama pada periode waktu yang berlainan (Wei [4]).

∑t=i (h - ̅)(Zt+k - ̅)

Pk=_∑ ‰ι(Zt - ̅) ²

dengan nilai Pk berkisar dari -1 sampai 1. Untuk fungsi PACF diberikan sebagai (Wei [4])

• _̂  _ ^p^ -∑J=I ∅̂k-1,JPk-J

• ^∅ kk ⁼  1-∑k~i ̂

• ^1-     ∅  ,

dengan   ∅^̂ k j = ∅^̂k-1,j-∅^̂kk ∅^̂ k-1,k-j untuk

j=1,2,3,…,k-1.

Uji Diagnostik Menggunakan Uji Ljung Box

Pada Uji Ljung Box akan dilakukan pengujian terhadap data apakah mempunyai unsur autokorelasi atau tidak, dengan tahapan: Menetapkan hipotesis yaitu,

^Ho :   =   =⋯=   =0 (data tidak

memiliki autokorelasi)

^l : minimal ada satu Pk≠0 (data memiliki autokorelasi)

Menghitung uji statistik Ljung-Box menggunakan persamaan sebagai berikut, (Wei[4])

LB =⁽" +2)∑( - I ) k=ι '      ⁷

dengan LB menyatakan statistik Ljung Box, n menyatakan banyaknya data pengamatan, ̂ k merupakan taksiran autokorelasi, dan m adalah panjang lag.

Daerah penolakan, Hq ditolak apabila LB > ^xa _;d f atau p-value < a . Apabila Hq ditolak

maka akan dipilih H^ yang berarti data berautokorelasi.

Pengujian Terhadap Kehadiran Efek ARCH-GARCH Menggunakan Uji ARCH LM

Uji ARCH LM dilakukan untuk melihat kehadiran unsur heteroscedasticity atau efek GARCH dengan tahapan:

Menetapkan hipotesis yaitu,

^o : homoscedasticity, tidak ada efek ARCH-GARCH

^l : heteroscedasticity, terdapat efek ARCH-GARCH

Menghitung nilai statistik uji ARCH LM menggunakan persamaan sebagai berikut (Rosadi [5]).

U=(n-m)R²

R² merupakan koefisien determinasi.

Daerah penolakan, Hq ditolak apabila U>

, atau P -value < a , yang berarti ada efek

ARCH-GARCH pada data

Model Terbaik AIC dan BIC

Dalam pemilihan model yang dihitung nilai AIC (Akaike’s Information Criterion) dan

BIC   (Bayesian   Information   Criterion)

seminimalnya (Wei [4]).

2k

AIC = ln ̂ a+

Il

dengan,  ̂ a  adalah estimasi maksimum

likelihood dari ^σa dan k merupakan

banyaknya parameter dalam model (Wei [4]).

BIC = ln(  )+k ln N+N+N ln(2π)

dengan SS merupakan Sum Square Error, k adalah banyaknya parameter, N adalah banyaknya residual dan π = 3,14

Generalized Autoregressive Conditional Heteroskedasticity (GARCH)

Model ARCH pada umumnya digunakan untuk memperkirakan volatilitas yang diperkenalkan oleh Engle pada tahun 1982 yang residualnya tidak saling berkorelasi.

Residual (^t) mengikuti model ARCH (^cI ) seperti pada persamaan berikut

^t =

Gt =  + βl^εt-l+⋯+βq^εt-q

Gt =  +

Cl

∑ βi^εt-i i=i

dengan βl,…,βq , dan ω merupakan parameter konstan. Bollerslev mengembangkan model ARCH menjadi model GARCH yang residualnya ( ^t ) mengikuti model GARCH (P, ^cI ) dengan ^cI merupakan orde ARCH dan P merupakan orde dari GARCH yang dapat dimodelkan sebagai (Bollerslev [1])

St =

Gt =  + ¾⅛1 +⋯+ ^p^t—p + βl^εt-l

+⋯+βq^εt-q

Untuk GARCH ( P, ^cI) variansnya dapat dirumuskan sebagai berikut (Bollerslev [1]):

Cl

G?

=  +

∑ «j Gt-j+∑βi^εt-i j=i          i=i

dengan a₁, a₂,…,^ap adalah nilai parameter ke j dari GARCH dan Gt-I, Gt-2,…,^σt~j adalah nilai varians ke t.

Non Linier GARCH (NGARCH)

Model     NGARCH     merupakan

pengembangan dari model GARCH, dimana memuat sebuah parameter ( y ) atau return innovations yang merupakan penyesuaian return saham. Secara umum, proses model NGARCH didefinisikan sebagai (Engle dan NG [6])

St=(-y)․√ℎt-l

G? =  + aσ²_t-₁ +β(^εt-l +Y√^σt-l)²

parameter-parameter dalam NGARCH yaitu ω merupakan parameter konstan, a merupakan parameter ARCH, β merupakan parameter GARCH dan Y parameter positif atau return innovations dari penyesuaian return saham.

Parameter NGARCH yaitu (ω,a,β,Y) merupakan bilangan positif dan a+ β(1+Y²)<1.

Value at Risk (VaR)

Untuk mengukur risiko dalam berinvestasi, konsep Value at Risk (VaR) digunakan sebagai alat ukur suatu risiko. VaR adalah kerugian yang dapat ditoleransi dengan tingkat kepercayaan tertentu. Keuntungan atau kerugian biasanya diasumsikan menyebar normal. Sebaran normal mempunyai dua parameter yaitu mean (µ) dan varians (σ²) (Hubbert [7]).

VaR_a = + σ² Φ ^-1 (α)

• 2.    METODE PENELITIAN

Sumber data yang digunakan dalam penelitian ini adalah data sekunder, yaitu data penutupan (close) dari penutupan IHSG yang diperoleh dari situs www.finance.yahoo.com dengan periode yang diambil adalah 3 tahun (1 Juli 2011 hingga 30 Juni 2014). Langkah-langkah dalam menentukan nilai VaR pada IHSG adalah sebagai berikut: (1) Menentukan tingkat pengembalian (return) data penutupan IHSG; (2) Mencari rataan, standar deviasi, skewness, dan kurtosis dari return penutupan IHSG untuk melihat karateristik data; (3) Melihat kestasioneran data penutupan IHSG menggunakan uji ACF dan PACF; (4) Melakukan uji diagnostik sebagai klarifikasi terhadap model yang akan diajukan apakah memiliki unsur autokorelasi atau tidak yang dikenal dengan Uji Ljung-Box; (5) Melakukan uji terhadap kehadiran efek heteroskedastik atau efek ARCH, yang dikenal uji ARCH LM; (6) Estimasi parameter (ω,a,β) pada model GARCH menggunakan MLE; (7) Pemilihan model terbaik menggunakan kriteria AIC dan BIC yang nilainya paling minimum; (8) Melakukan simulasi pada parameter GARCH ( ̅, ̅, ^̅); (9) Menentukan nilai VaR menggunakan nilai ^σt yang telah didapat; (10) Melakukan estimasi terhadap parameterparameter (ω,a,β,Y ) menggunakan MLE untuk menentukan parameter-parameter dari

model NGARCH; (11) Melakukan simulasi pada parameter NGARCH ( ̅, ̅, ^̅, ̅); (12) Menentukan nilai VaR menggunakan nilai ^σt yang telah didapat; dan (13) Membandingkan nilai VaR yang didapat melalui simulasi model GARCH dengan nilai VaR model NGARCH dalam menentukan risiko saham.

• 3.    HASIL DAN PEMBAHASAN

Perhitungan return data penutupan saham IHSG periode 1:

, =    (   ^, ≤)

^,t      Vi,t-ι∕

= 0․006705081

Untuk nilai        , selanjutnya dengan

1≤t≤727 dihitung dengan menggunakan software Matlab 2009 dan berikut adalah plot data return IHSG

0.06

0.04

0.02

0

⅛ -0.02

-0.04

-0.06

-0.08

-0.1

Juli 2011 Des 2011 Juni 2012 Des 2012 Juni 2013 Des 2013 Juni 2014 periode

Penggunaan model GARCH yang digunakan dalam meramalkan model data yang bersifat acak dan volatilitasnya tidak konstan perlu memerhatikan langkah-langkah sebagai berikut, yaitu tahap pra-estimasi dengan melakukan uji terhadap autokorelasi data pada Tabel 1 dan Tabel 2.

Tabel 1. Uji Ljung-Box Residual Kuadrat

Uji Ljung-Box Kuadrat
p-value	Q Stat	CV
0.0084	6.9527	3.8415
0.0000	64.9910	11.0705
0.0000	147.8295	16.9190
0.0000	177.7850	22.3620
0.0000	186.1346	27.5871
0.0000	210.1614	32.6706

Tabel 2. Uji ARCH LM

Uji ARCH LM
p-value	Q Stat	CV
0.0085	6.9158	3.8415
0.0000	51.4033	11.0705
0.0000	99.3323	16.9190
0.0000	102.9587	23.6848
0.0000	103.6609	27.5871
0.0000	119.6826	32.6706

Dari Tabel 1 dan Tabel 2, bahwa berdasarkan Uji Ljung-box residual kuadrat dan uji ARCH LM terhadap nilai dugaan residual kuadratnya diperoleh bahwa nilai Q Stat lebih besar dari Critical Value (CV) atau nilai p-value lebih kecil dari a = 0,05 yang mengindikasikan tolak Hq atau terima H^ yang artinya nilai dugaan residual kuadrat IHSG berautokorelasi dan terdapat efek ARCH-GARCH pada data return saham IHSG sehingga memungkinkan peramalan menggunakan model GARCH. Penentuan orde GARCH dapat dilihat dari plot ACF dan PACF residual kuadrat pada gambar berikut.

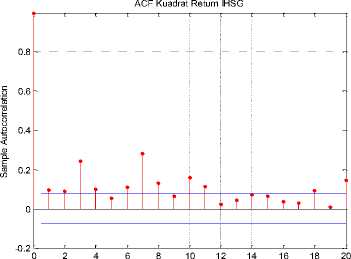
Lag

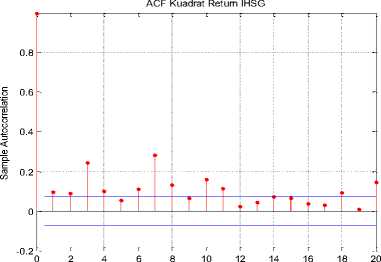
Lag

Model GARCH yang dibentuk dari ACF dan PACF residual kuadrat.

Tabel 3. Estimasi Parameter Model GARCH

Model	GARCH (1,1)	GARCH (1,2)	GARCH (2,1)	GARCH (2,2)
K (ω)	2.3923 × 10-6 [2.4043]*	2.4656 × 10-6 [2.4442]*	2.4131 × 10-6 [1.8582]*	3.9373 × 10-6 [2.0686]*
G1 (a1)	0.8673 [33.3551]*	0.86412 [31.6870]*	0.86883 [2.4760]*	0 0
G2 ( 122 )	-	-	0 0	0.76065 [6.0562]*
ft ( ft )	0.121619 [4.7071]*	0.11072 [2.5457]*	0.12645 [2.7789]*	0.09869 [2.9668]*
^2 ( ft )	-	0.018399 [0.4220]	-	0.13231 [4.9408]*
AIC	-4.4964	-4.4945	-4.4944	-4.4938
BIC	-4.4826	-4.4772	-4.4771	-4.4731

Keterangan: tanda […]^∗ menunjukkan T-Stat > T-

tab pada a = 0,05

Diketahui hasil estimasi koefisien model GARCH IHSG, dimana peramalan menggunakan model GARCH (1,1) paling baik dibanding model GARCH yang lainnya. Hal ini dapat dilihat dari uji AIC dan BIC yang memberikan nilai paling minimum pada peramalan model GARCH (1,1). Sehingga model GARCH (1,1) pada IHSG adalah

Ot =  + βj^σt-j + a_tεt-ι

Ot =2․3923×10 -6 + 0․8673^σt-ι

+ 0․121619^εt-ι

Setelah memperoleh parameter terbaik dari model GARCH akan dilakukan simulasi untuk menentukan parameter VaR ( V^t- , σ²) dalam menentukan risiko. perhitungan nilai VaR menggunakan tingkat kepercayaan 95% dan 99% dengan periode waktu yang digunakan adalah 1 hari, 10 hari, dan 22 hari

VaR_a =  + σ² Φ -¹(α) ×√t

Nilai VaR pada simulasi model GARCH dapat dilihat pada Tabel 4 dan Tabel 5.

Tabel 4. Nilai VaR GARCH a = 0.05

Tingkat Kepercayaan a = 0.05
Simulasi	1 hari	10 hari	22 hari
100	-0.1080	-0.3416	-0.5067
1000	-0.1162	-0.3673	-0.5448
10.000	-0.1200	-0.3794	-0.5628

Tabel 5. Nilai VaR GARCH a = 0.01

Tingkat Kepercayaan a = 0.01
Simulasi	1 hari	10 hari	22 hari
100	-0.1457	-0.4607	-0.6834
1000	-0.1655	-0.5233	-0.7761
10.000	-0.1700	-0.5375	-0.7975

Tabel 7. Parameter Model NGARCH dengan MLE

Parameter	Nilai
K ( ω)	3.8991 × 10-6
Gi (a)	0.0956
_ Ai (£)	0.8411
_ y	0.6542

Berdasarkan Tabel 4 dan Tabel 5, terlihat bahwa nilai VaR terkecil diperoleh pada periode horizon 1 hari, ini artinya apabila jangka waktu investasi yang dilakukan singkat, maka risiko yang ditanggung akan semakin kecil, tetapi semakin lama jangka investasi maka investor menanggung risiko yang lebih besar.

Model      NGARCH       dalam

pengembangannya memuat sebuah parameter gamma (y) yang bersifat positif atau return innovations. Parameter y (return innovations) dapat meng-urangi dampak good news yang variansnya lebih besar dari nol ( σ_t _ ₁ > 0) dan meningkatkan pengaruh terhadap dampak bad news dimana varians lebih kecil dari nol (^σt_ 1 < ⁰⁾.

∑^t- 1 ^IHSG, t y =-------- ^σIHSG,t

= 0.000539

Setelah memperoleh nilai parameter y maka akan dibentuk sebuah parameter awal pada model NGARCH.

Tabel 6. Parameter Awal Model NGARCH

Parameter	Nilai
K (ω)	2.3923 × 10-6
Gi («)	0.8673
A i (β)	0.121619
y	0.000539

Setelah dibentuknya parameter awal NGARCH akan diestimasi menggunakan metode Maximum Likelihood Estimation (MLE) untuk memperoleh parameter optimal dari model NGARCH dengan menggunakan software MATLAB 2009 diperoleh parameter optimal model NGARCH

Setelah mendapatkan parameter optimal akan dilakukan simulasi untuk menentukan parameter VaR dalam menentukan risiko. Tingkat kepercayaan yang digunakan dalam perhitungan nilai VaR adalah 95% dan 99% dan periode waktu yang digunakan adalah 1 hari, 10 hari, dan 22 hari.

Tabel 8. Nilai VaR NGARCH a = 0.05

Tingkat Kepercayaan a = 0.05
Simulasi	1 hari	10 hari	22 hari
100	-0.0384	-0.1215	-0.1802
1000	-0.0425	-0.1346	-0.1997
10.000	-0.0441	-0.1396	-0.2070

Tabel 9. Nilai VaR NGARCH a = 0.01

Tingkat Kepercayaan a = 0.01
Simulasi	1 hari	10 hari	22 hari
100	-0.0445	-0.1565	-0.2322
1000	-0.0590	-0.1865	-0.2767
10.000	-0.0619	-0.1959	-0.2905

Berdasarkan Tabel 8 dan Tabel 9, terlihat bahwa nilai VaR terkecil diperoleh pada periode horizon 1 hari, ini artinya apabila jangka waktu investasi yang dilakukan singkat, maka risiko yang ditanggung akan semakin kecil, tetapi semakin lama jangka investasi maka investor menanggung risiko yang lebih besar.

Pengertian dari Value at Risk (VaR) yaitu kerugian terburuk dari suatu aset tunggal maupun portofolio pada jangka waktu tertentu dengan tingkat kepercayaan tertentu, dengan melihat hasil nilai VaR dari model GARCH dan model NGARCH maka diketahui semakin lama jangka waktu investasi dan semakin besar tingkat kepercayaan yang diberikan maka diperoleh nilai VaR yang semakin besar. Setelah diperoleh nilai VaR model GARCH dan model NGARCH sekarang akan dilihat

perbandingan nilai VaR yang diperoleh dari kedua model tersebut pada Tabel 10.

Tabel 10. Perbandingan Nilai VaR Model

GARCH dan Model NGARCH dengan Periode Horizon 1 Hari, 10 Hari, dan 22 Hari.

Periode Horizon 1 Hari
Simulasi	(a = 0.05)
	GARCH	NGARCH
100	-0.1080	-0.0384
1000	-0.1162	-0.0426
10000	-0.1200	-0.0441
Simulasi	(a = 0.01)
	GARCH	NGARCH
100	-0.1457	-0.0445
1000	-0.1655	-0.0590
10000	-0.1700	-0.0619
Periode Horizon 10 Hari
Simulasi	(a = 0.05)
	GARCH	NGARCH
100	-0.3416	-0.1215
1000	-0.3673	-0.1346
10000	-0.3794	-0.1396
Simulasi	(a = 0.01)
	GARCH	NGARCH
100	-0.4607	-0.1565
1000	-0.5233	-0.1865
10000	-0.5375	-0.1959
Periode Horizon 22 Hari
Simulasi	(a = 0.05)
	GARCH	NGARCH
100	-0.5067	-0.1802
1000	-0.5448	-0.1997
10000	-0.5628	-0.2070
Simulasi	(a = 0.01)
	GARCH	NGARCH
100	-0.6834	-0.2322
1000	-0.7761	-0.2767
10000	-0.7975	-0.2905

Keterangan: tanda (-) menunjukkan kerugian

Pada Tabel 10 dapat diketahui bahwa nilai VaR menggunakan model GARCH dan model NGARCH dengan periode horizon 1 hari, 10 hari, dan 22 hari dengan tingkat kepercayaan yang berbeda didapat nilai VaR model NGARCH lebih kecil dibandingkan nilai VaR model GARCH.

Pemilihan tingkat kepercayaan yang berbeda terhadap perhitungan VaR pada kedua model seperti Tabel 10 terlihat bahwa nilai

VaR terkecil diperoleh dengan tingkat kepercayaan 95%, dimana ini menandakan semakin besar tingkat kepercayaan investor terhadap investasi yang dipilih maka semakin besar juga risiko yang akan ditanggung.

• 4.    SIMPULAN DAN SARAN

Berdasarkan uraian pada hasil dan pembahasan, maka diperoleh simpulan, yaitu:

Perhitungan nilai VaR model GARCH tingkat kepercayaan 95% (a = 0,05) dengan periode horizon 1 hari, 10 hari, 22 hari secara berturut-turut -0.1080, -0.3416, dan -0.5067. Sedangkan pada tingkat kepercayaan 99% ( a = 0,01) dengan periode horizon 1 hari, 10 hari, 22 hari secara berturut-turut -0.1457, -0.4607, dan -0.6834.

Pada model NGARCH nilai VaR dengan tingkat kepercayaan 95% (a = 0,05) dengan periode horizon 1 hari, 10 hari, 22 hari secara berturut-turut -0.0384, -0.1215, dan -0.1802. Sedangkan pada tingkat kepercayaan 99% ( a = 0,01) dengan periode horizon 1 hari, 10 hari, 22 hari secara berturut-turut -0.0445,0.1565, dan -0.2322. Nilai VaR model NGARCH lebih kecil dibandingkan model GARCH.

Disarankan pada penelitian berikutnya mencermati kondisi ekonomi yang mempengaruhi harga saham. Hal ini bisa dilakukan dengan menggunakan data dimana kondisi data ekonominya naik dan turun.

DAFTAR PUSTAKA

• [1]    Bollerslev, T., 1986. Generalized Autoregresif Conditional Heterosk-edasticity. Journal of Econometric, pp.307-27

• [2]    Brigo, D., Dalessandro, A., Neugebauer, M. dan Triki, F., 2007. A Stochastic Processes Toolkit for Risk Management. pp.3-17.

• [3]    Husnan, S., 2003. Dasar-Dasar Teori Portofolio dan Analisis Sekuritas. Yogyakarta: AMP YKN.

• [4]    Wei, W.W.S., 2006. Time Series Analysis: Univariate and Multivariate Methods. 2nd ed. New Jersey: Pearson Prentice Hall.

• [5]    Rosadi, D., 2012. Ekonometrika dan Analisis Runtun Waktu Terapan dengan EViews. Yogyakarta: Penerbit ANDI.

• [6]    Engle, R.F. dan NG, V.K., 1993. Measuring and Testing the Impact of News on Volatility. The Journal of Finance, XLVIII, pp.1749-78.

• [7]    Hubbert, S., 2012. Essential Mathematics for Market Risk Management (2nd Edition). USA: Hoboken, N.J. : Wiley.

66