E-Jurnal Matematika Vol. 4 (1), Januari 2015, pp. 8-13

ISSN: 2303-1751

PERBANDINGAN TRANSFORMASI BOX-COX DAN REGRESI KUANTIL MEDIAN DALAM MENGATASI HETEROSKEDASTISITAS

Ni Wayan Yuni Cahyani§1, I Gusti Ayu Made Srinadi2, Made Susilawati3

1Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]] 2Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]] 3Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: [email protected]]

§Corresponding Author

ABSTRACT

Ordinary least square (OLS) is a method that can be used to estimate the parameter in linear regression analysis. There are some assumption which should be satisfied on OLS, one of this assumption is homoscedasticity, that is the variance of error is constant. If variance of the error is unequal that so-called heteroscedasticity. The presence heteroscedasticity can cause estimation with OLS becomes inefficient. Therefore, heteroscedasticity shall be overcome. There are some method that can used to overcome heteroscedasticity, two among those are Box-Cox power transformation and median quantile regression. This research compared Box-Cox power transformation and median quantile regression to overcome heteroscedasticity. Applied Box-Cox power transformation on OLS result R2point are greater, smaller RMSE point and confidencen interval more narrow, therefore can be concluded that applied of Box-Cox power transformation on OLS better of median quantile regression to overcome heteroscedasticity.

Keywords: Heteroscedasticity, OLS, Box-Cox power transformation and Median Quantile Regression.

  • 1.    PENDAHULUAN

Estimasi parameter pada analisis regresi linear dilakukan dengan menggunakan Metode Kuadrat Terkecil. Pendugaan parameter regresi dengan metode kuadrat terkecil memiliki beberapa asumsi yang harus dipenuhi agar mendapatkan penduga yang bersifat Best Linear Unbiased Estimator (BLUE). Salah satu asumsi tersebut adalah homoskedastisitas yang berarti nilai varians dari galat adalah sama (konstan). Apabila asumsi nilai varians dari galat tidak konstan maka dikatakan terjadi heteroskedastisitas.

Adanya heteroskedastisitas dapat menyebabkan pendugaan parameter dengan menggunakan metode kuadrat terkecil tidak dapat menghasilkan penduga yang memenuhi sifat BLUE sehingga model yang diperoleh

menjadi tidak efisien dan tidak dapat dipercaya (Gujarati [2]). Oleh karena itu, keberadaan heteroskedastisitas harus diatasi. Terdapat beberapa metode yang dapat digunakan untuk mengatasi heteroskedastisitas, antara lain Transformasi Box-Cox dan regresi kuantil median.

Penelitian tentang kemampuan transformasi Box-Cox dalam mengatasi heteroskedastisitas telah dilakukan oleh Ispriyanti [3] dan Kristina [6]. Dari penelitian tersebut disimpulkan bahwa transformasi Box-Cox dapat digunakan untuk mengatasi heteroskedastisitas dengan nilai λ berada pada interval (-2, 2), dan penelitian tentang regresi kuantil median untuk mengatasi heteroskedastisitas pernah dilakukan oleh Uthami, et. al [8].

Pada penelitian ini penulis ingin membandingkan kemampuan transformasi

Box-Cox dan regresi kuantil median dalam mengatasi masalah heteroskedastisitas dan untuk melihat metode mana yang lebih baik dalam menangani heteroskedastisitas. Data yang digunakan dalam penelitian ini adalah data tentang lama pasien bertahan hidup setelah melakukan operasi liver tertentu yang diperoleh dari buku Neter, et. al [7] halaman 202 – 203.

  • 1.1    Metode Kuadrat Terkecil

Metode kuadrat terkecil adalah metode yang bertujuan untuk meminimumkan jumlah kuadrat galat (sum square error). Pendugaan koefisien regresi linear berganda dengan metode kuadrat terkecil dapat dilakukan dengan menggunakan persamaan matriks (Neter, et. al [7]), sebagai berikut:

b = (XrX)-1JTt Y               (1)

dan untuk mencari selang kepercayaan pada metode kuadrat terkecil dapat dilakukan melalui persamaan:

  • bi ± *‰√*{M∙             (2)

  • 1.2    Transformasi Box-Cox

Transformasi Box-Cox

merupakan


transformasi pangkat pada variabel respons yang dikembangkan oleh Box dan Cox, yang bertujuan untuk menormalkan data, melinearkan model regresi dan menghomogenkan varians. Box dan Cox mempertimbangkan kelas transformasi berparameter tunggal, yaitu A yang dipangkatkan pada variabel respons Y, sehingga diperoleh model transformasinya Yλ dengan λ merupakan parameter yang harus diduga. Transformasi Box-Cox hanya diberlakukan pada variabel respons Y yang bertanda positif (Draper & Smith [1]). Prosedur utama yang dilakukan pada Transformasi Box-Cox adalah menduga parameter λ, yang dilakukan dengan mencari nilai Wi dan Vi melalui persamaan:

Wi =

Ilny

; untuk A ≠ O

; untuk A = O

(3)

1^= i

^S^ ^

; un tuk A ≠ 0

(4)

‰ InK

; untuk A = O

dengan Ygβo = ψ1Y2-Yn = (TWi);.

Selanjutnya meregresikan antara K dan X sehingga diperoleh nilai JKG dan nilai A yang dipilih adalah A yang menghasilkan nilai JKG terkecil. Setelah itu dilakukan transformasi pada variabel respon Y dengan nilai A yang telah di pilih. Pada tabel berikut disajikan nilai A dan model transformasinya.

Tabel 1. Nilai A dan Model Transformasinya

Nilai                 \

Model tranformasi

-2

-1

r4

-0.5

y-C ≡ _ ’      √F

O

y° = in y

0.5

yθ.5 _ ^'y

1

y1 = y

2

Y1 = Y2

Sumber: Neter, et al.(1997)

  • 1.3    Regresi Kuantil Median

Regresi kuantil median adalah metode yang mendefinisikan median sebagai solusi untuk meminimumkan jumlah galat mutlak (Koenker & Basset [4]). Kuantil dapat dioperasikan dengan penyusunan atau pengurutan sampel pengamatan sehingga lebih mudah menentukan letaknya dan dapat mendefinisikan kuantil melalui alternatif yang sederhana sebagai masalah optimasi.

Untuk mendefinisikan regresi kuantil median dalam model dengan sampel acak {yi-y^ys-—yJ digunakan persamaan:

mi⅛eΛ∑"=ι(y≈ -μ)2           (5)

Sehingga diperoleh rata-rata sampel yang merupakan pengestimasian dari rata-rata populasi E(FIX) . Jika skalar μ=Xiβ maka

persamaan (5) menjadi:

∏⅛ΛP∑Γ=ι(yi -^)2

(6)


Dengan ^i merupakan variabel bebas ke~i, β merupakan parameter, dan y⅛ merupakan variabel respons ke—i.

Penelitian yang dilakukan Koeker dan Basset juga membahas masalah regresi tersebut,

yang kemudian berkembang menjadi median sampel yang dinyatakan dalam persamaan:


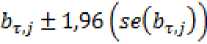
(12)


mln ∑p=1∣yi-X^∣ p CΛr


(7)


Kemudian secara umum dispesifikasikan dalam fungsi kuantil bersyarat ke-T dapat mempertimbangkan penduga bagi AW yaitu (aw) sehingga diperoleh ide bahwa masalah tersebut dapat dinyatakan pada persamaan:

mi∏∑"=1prC½ - <λ (TlW) p Ct∖P

(8)


Dengan τ adalah indeks kuantil ∈(04) , Pt

adalah loss function yang asimetrik, dan ρi(r∣τ) = TAW merupakan fungsi kuantil ke– τ dari Y dengan syarat X

Jika Y merupakan sebaran variabel acak kontinu dan x adalah salah satu vektor regresor X, maka fungsi kuantil bersyarat dalam fungsi kuantil ke-τ dapat didefinisikan sebagai:

ρi(F∣T) = inf{y: Fy(y∣W≥τ}      (9)

denganFy(ylW = fungsi sebaran dari Y dengan

syarat X dan fungsi kepekatan bersyaratnya ⅛(ylW .

Regresi kuantil median mengembangkan persamaan sederhana untuk regresor X. Dalam hal ini diasumsikan spesifikasi linear untuk kuantil bersyarat dari variabel respons Y untuk p vektor variabel bebas X.

ρ(⅛,AW) =TiAW (10) denganAW adalah vektor koefisien pada

kuantil ke–T.

Untuk meminimalkan kuantil tidak bersyarat di atas dengan estimasi regresi kuantil median adalah:

Aω = argmin<τ){∑ipτ(yi - TiA(τ})) (11)

Untuk mencari selang kepercayaan pada regresi kuantil median terdapat tiga metode yang dapat digunakan yaitu metode sparsity, metode rank dan metode bootstrap. Pada penelitian ini yang digunakan untuk membangun selang kepercayaan adalah metode bootstrap yaitu dengan melakukan proses bootstrap yang kemudian hasilnya akan dimasukan ke dalam batas distribusi normal dengan batas yang sudah ditentukan, yaitu:

  • 1.4    Root Mean Square Error (RMSE)

RMSE adalah suatu indikator yang dapat digunakan untuk mengukur tingkat akurasi pendugaan suatu model. RMSE juga dapat menyatakan besarnya galat yang dihasilkan suatu model dugaan. RMSEberarti galat dari data yang diperoleh dikuadratkan, dicari rata-ratanya kemudian diakarkan. Dari sekumpulan data Tp (p = 1,2.....W untuk mendapatkan nilai RMSE maka digunakan persamaan:

RMSE = J^+⅛5+¾≡*^+⅛≡      (13)

Semakin kecil nilai RMSE berarti galat semakin kecil sehingga model yang diperoleh semakin baik.

  • 2.    METODE PENELITIAN

Langkah-langkah yang dilakukan pada penelitian ini adalah:

  • 1.    Mencari data yang memiliki masalah heteroskedastisitas.

  • 2.    Menerapkan Transformasi Box-Cox untuk mengatasi heteroskedastisistas dengan langkah-langkah sebagai berikut:

  • a.    Menentukan nilai λ pada rentang (-2,2)

  • b.    Melakukan transformasi terhadap variabel Y sesuai dengan nilai λ yang didapatkan. Nilai λ yang dipilih adalah nilai λ yang menghasilkan nilai Jumlah Kuadrat Galat (JKG) terkecil.

  • c.    Melakukan uji heteroskedastisitas pada model yang diperoleh dari estimasi dengan Transformasi Box–Cox.

  • d.    Mencari selang kepercayaan parameter

  • e.    Mencari nilai RMSE

  • 3.    Menerapkan Regresi Kuantil Median untuk mengatasi heteroskedastisitas dengan langkah-langkah:

  • a.    Melakukan estimasi parameter dengan menggunakan Regresi Kuantil Median dimana estimasi dilakukan pada setiap kuantil  ke-τ  untuk masing-masing

koefisien regresi.

  • b.    Melakukan uji heteroskedastisitas pada model yang diperoleh dari estimasi dengan Regresi Kuantil Median.

  • c.    Mencari selang kepercayaan parameter dengan metode Bootstrap dengan replikasi minimal 100000 kali, kemudian mencari nilai selang kepercayaan.

  • d.    Mencari nilai RMSE

  • 4.    Membandingkan hasil dari Transformasi Box–Cox dan Regresi Kuantil Median berdasarkan nilai , RMSE dan selang kepercayaan yang diperoleh.

  • 3.    HASIL DAN PEMBAHASAN

    • 3.1    Pengujian Heteroskedastisitas Data

Heteroskedastisitas merupakan suatu keadaan apabila varians dari galat tidak konstan.

Keberadaan      heteroskedastisitas

menyebabkan estimasi dengan OLS tidak efisien. Untuk melihat heteroskedastisitas dapat dilakukan

dapat menjadi adanya dengan


melihat pola antara galat dengan nilai dugaannya. Plot untuk data dapat dilihat pada gambar berikut:

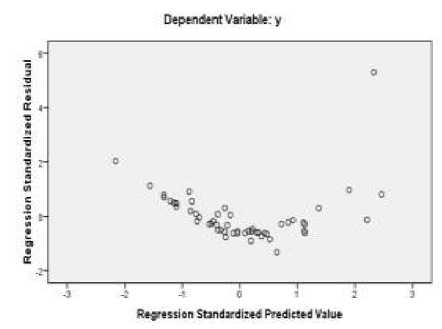
Gambar 1. Plot Varians dari Galat untuk Data

Pada Gambar 1 tampak bahwa galat tidak tersebar secara merata di atas dan di bawah nol (0), yang mengindikasikan adanya masalah heteroskedastisitas pada data. Namun, untuk mendapatkan hasil yang lebih pasti dapat dilakukan pengujian secara formal.

Pengujian formal pada data menggunakan uji White yang dilakukan dengan meregresikan galat kuadrat dengan variabel bebas, variabel

bebas yang dikuadratkan dan perkalian silang antara variabel bebasnya, kemudian nilai dikalikan dengan jumlah pengamatan untuk mendapatkan nilai            . Jika nilai

maka keputusannya adalah

menolak hipotesis nol. Hipotesis yang digunakan adalah:

  • H0 :

H1 : Paling tidak terdapat dua varians yang

berbeda

Hasil pengujian terhadap adanya heteroskedastisitas pada data diperoleh nilai

37,88840,     dengan     nilai

. Karena                maka

keputusannya adalah menolak hipotesis nol sehingga         disimpulkan        terdapat

heteroskedastisitas pada data.

  • 3.2    Penerapan Transformasi Box-Cox

Transformasi Box-Cox merupakan transformasi pangkat pada variabel respons yang hanya dapat dilakukan pada variabel respons yang bertanda positif. Prosedur utama yang dilakukan pada transformasi Box-Cox adalah menduga parameter A dengan nilai λ berada pada interval nilai (-2, 2), λ yang digunakan adalah λ yang menghasilkan nilai JKG terkecil. Untuk melakukan proses transformasi digunakan program Minitab 16. Nilai λ yang digunakan untuk transformasi data dapat dilihat pada Gambar berikut:

Box-Cox Plot of y

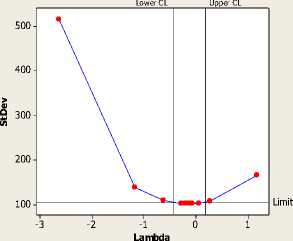
Lambda

(using 95.0% confidence)

Estimate           -0.14

Lower CL       -0.44

Upper CL        0.19

Rounded Value    0.00

Gambar 2. Plot dalam Transformasi Box-Cox

Dari gambar dapat dilihat bahwa nilai λ berada pada interval -0.44 < λ < 0.19 Interval nilai λ melalui nilai λ = 0 sehingga dilakukan

transformasi dengan nilai A = 0, berdasarkan Tabel 1 maka model transformasi yang digunakan adalah ln V. Setelah dilakukan proses transformasi pada variabel respons, kemudian dilakukan estimasi dengan OLS pada data tersebut. Hasil estimasi menghasilkan model:

V = £(1.125360 + 0.157788X1 +

0.021309X2 + 0.021816X3)

Nilai R2 yang dihasilkan adalah sebesar 97.2% yang berarti semua variabel bebas yang digunakan dalam model dapat menjelaskan variabel respon sebesar 97.2%. Nilai RMSE yang diperoleh adalah sebesar 0.1038.

Kemudian untuk mengetahui apakah masalah heteroskedastisitas dapat diatasi maka dilakukan pengujian heteroskedastisitas pada hasil estimasi dengan OLS. Uji yang digunakan untuk mendeteksi heteroskedastisitas adalah uji White. Hasil pengujian terhadap adanya heteroskedastisitas dengan uji White memberikan nilai χ2hitung=16.8111 sedangkan nilai tabel 16.919. Karena nilai X2hitung < X2tabel maka keputusannya adalah menerima hipotesis nol yang berarti tidak terdapat heteroskedastisitas. Hal ini menunjukkan bahwa transformasi Box-Cox dapat mengatasi masalah heteroskedastisitas.

  • 3.3    Estimasi dengan Regresi Kuantil

Regresi kuantil median merupakan metode yang mendefinisikan median sebagai solusi untuk meminimumkan jumlah galat mutlak. Metode ini bersifat fleksibel dalam memodelkan data dengan masalah heteroskedastisitas dan dapat langsung digunakan untuk menduga parameter pada data dengan masalah heteroskedastisitas. Hasil estimasi dengan regresi kuantil median menghasilkan model:

V = -481.4768 + 29.31897X1 +

3.035971X2 + 3.357251X3

Nilai R2 yang dihasilkan sebesar 66% yang berarti semua variabel bebas yang digunakan dalam model dapat menjelaskan variabel respon sebesar 66%, dan nilai RMSE yang diperoleh adalah sebesar 63.47917.

Model yang dihasilkan dari estimasi dengan regresi kuantil median kemudian diuji dengan uji White untuk melihat apakah model mengandung heteroskedastisitas atau tidak. Hasil pengujian memberikan nilai X2hitung 30.92618 sedangkan nilai X tabel= 16.919.Karena X hitung> X tabel maka keputusannya adalah menolak hipotesis nol, sehingga disimpulkan terdapat heteroskedastisitas pada model yang diperoleh. Hal ini menunjukkan estimasi dengan regresi kuantil median masih mengandung masalah heteroskedastisitas.

Walaupun tidak dapat menghilangkan heteroskedastisitas tetapi regresi kuantil median tetap dapat digunakan untuk estimasi pada data dengan masalah heteroskedastisitas dan model yang dihasilkan juga efisien karena regresi kuantil median tidak memerlukan asumsi homoskedastisitas dan merupakan metode yang fleksibel terhadap kasus heteroskedastisitas.

  • 3.4    Perbandingan Transformasi Box-Cox dan Regresi Kuantil Median

Penelitian ini menggunakan tiga indikator untuk mengetahui metode yang lebih baik dalam menangani masalah heteroskedastisitas yaitu nilai R2, nilai RMSE dan selang kepercayaan. Metode yang lebih baik adalah metode yang menghasilkan nilai R2 lebih besar, nilai RMSE yang lebih kecil dan lebar selang kepercayaan yang lebih sempit. Perbandingan untuk kedua metode dapat dilihat pada Tabel berikut:

Tabel 2. Perbandingan Nilai R2 dan RMSE

R2

RMSE

OLS

Regresi Kuantil

OLS

Regresi Kuantil

97.2%

66%

0.1038

63.4791

Berdasarkan Tabel 2 terlihat bahwa penerapan transformasi Box-Cox pada OLS menghasilkan nilai R2 sebesar 97.2% dan nilai RMSE sebesar 0,103828, sedangkan estimasi dengan regresi kuantil median menghasilkan nilai R2 sebesar 66% dan nilai RMSE sebesar 63.4791. Untuk lebar selang kepercayaan dapat dilihat pada tabel berikut:

Tabel 3. Perbandingan Selang Kepercayaan

Lebar Selang Kepercayaan

Parameter

OLS

Regresi Kuantil

k

0.057898

30.67955

0.00465

2.3463

Pa

0.00422

2.027028

P*

0.103344

40.14601

Karena penerapan transformasi Box-Cox pada OLS menghasilkan nilai R2 yang lebih besar, nilai RMSE yang lebih kecil dan lebar selang kepercayaan yang lebih sempit, sehingga disimpulkan bahwa transformasi Box-Cox lebih baik digunakan untuk mengatasi heteroskedastisitas pada data.

  • 4.    KESIMPULAN DAN SARAN

Dari hasil yang diperoleh diketahui bahwa penerapan transformasi Box-Cox pada OLS menghasilkan nilai R2 lebih besar, nilai RMSE lebih kecil dan lebar selang kepercayaan lebih sempit dibandingkan dengan yang dihasilkan oleh estimasi dengan regresi kuantil median. Oleh karena itu, dapat disimpulkan bahwa kemampuan transformasi Box-Cox lebih baik untuk mengatasi heteroskedastisitas.

Untuk lebih memastikan kemampuan dari metode transformasi Box-Cox dan regresi kuantil median disarankan untuk menggunakan data yang dihasilkan dari membangkitkan data dengan masalah heteroskedastisitas.

DAFTAR PUSTAKA

  • [1]    Draper, N. R. & Smith, H., 1998. Applied regression Analysis. Third ed. New York: John Wiley.

  • [2]    Gujarati, D. N, 2004. Basic Econometrics. 4th ed. New York: The McGrawHill Companies.

  • [3]    Ispriyanti, D., 2004. Pemodelan Statistika dengan Transformasi Box - Cox. Jurnal Matematika dan Komputer, Volume 7, pp. 8-17.

  • [4]    Koenker, R.&Basset, J. 1978. Regression Quantiles. Econometrica, 46(1), pp. 35-50.

  • [5]    Koenker,R & Hallock,K.F, 2001. Quantile Regression. Journal of Economic Perspectives, 15(4), pp. 143 - 156.

  • [6]    Kristina, S., 2011. Analisis Transformasi Box-Cox untuk Mengatasi Heteroskedastisitas dalam Model Regresi Linier Sederhana. Skripsi, Medan: Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatra Utara.

  • [7]    Neter, J., Wasserman, W. & Kutner, M. H., 1997. Model Linier Terapan Buku I dan II: Analisis Regresi Linier Sederhana dan Analisis Regresi Ganda, diterjemahkan oleh Bambang Sumantri. Bogor: Jurusan Statistika FMIPA IPB.

  • [8]    Uthami, I. P., Sukarsa, I. dan Nila Kencana, I. E., 2013. Regresi Kuantil Median untuk Mengatasi Heteroskedastisitas pada Analisis Regresi. E-Jurnal Matematika, 2(1), pp. 616

13