KOMPARASI KINERJA FUZZY TIME SERIES DENGAN MODEL RANTAI MARKOV DALAM MERAMALKAN PRODUK DOMESTIK REGIONAL BRUTO BALI
on
E-Jurnal Matematika Vol 3 (3), Agustus 2014, pp. 116-122
ISSN: 2303-1751
KOMPARASI KINERJA FUZZY TIME SERIES
DENGAN MODEL RANTAI MARKOV DALAM MERAMALKAN PRODUK DOMESTIK REGIONAL BRUTO BALI
I Made Arya Antara1, I Putu Eka N. Kencana§2, I Komang Gde Sukarsa3
-
1 Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: genezisdragonoid@gmail.com]
-
2 Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: i.putu.enk@gmail.com]
-
3 Jurusan Matematika, Fakultas MIPA – Universitas Udayana [Email: sukarsakomang@yahoo.com]
-
§ Corresponding Author
ABSTRACT
This paper aimed to elaborates and compares the performance of Fuzzy Time Series (FTS) model with Markov Chain (MC) model in forecasting the Gross Regional Domestic Product (GDRP) of Bali Province. Both methods were considered as forecasting methods in soft modeling domain. The data used was quarterly data of Bali’s GDRP for year 1992 through 2013 from Indonesian Bureau of Statistic at Denpasar Office. Inspite of using the original data, rate of change from two consecutive quarters was used to model. From the in-sample forecasting conducted, we got the Average Forecasting Error Rate (AFER) for FTS dan MC models as much as 0,78 percent and 2,74 percent, respectively. Based-on these findings, FTS outperformed MC in in-sample forecasting for GDRP of Bali’s data.
Keywords: domestic product, fuzzy modeling, in-sample forecasting, Markov chain
Badan Pusat Statistik (BPS) mendefinisikan Produk Domestik Regional Bruto (PDRB) sebagai jumlah nilai tambah barang dan jasa yang dihasilkan seluruh unit usaha di suatu daerah [1]. PDRB lazim digunakan sebagai salah satu indikator penting untuk mengetahui perkembangan perekonomian di suatu wilayah.
Sebagai sebuah ukuran, PDRB berperan penting sebagai salah satu masukan pada rancangan program-program pembangunan daerah. Melalui PDRB dan indikator-indikator penyusunnya, para pengambil kebijakan publik dapat merancang rencana dan program-program pembangunan yang lebih terarah dan terfokus pada peningkatan kesejahteraan masyarakat. Mengacu kepada hal ini, maka usaha untuk menduga nilai PDRB dengan merujuk nilai-nilai PDRB historis semakin intensif dilakukan.
Pada umumnya, teknik peramalan yang diaplikasikan untuk menduga PDRB adalah teknik peramalan yang tergolong ke dalam teknik analisis deret waktu klasik. Sebagai misal, Wana-yasa et al. menduga PDRB Provinsi Bali atas dasar harga konstan (adhk) tahun 2011 dari data PDRB Bali periode 1991–2010 menggunakan metode pemulus eksponensial Holt-Winter aditif.
Hasil peramalannya menunjukkan nilai Average Forecasting Error Rate (AFER) dari metode ini sebesar 7,13 persen [2].
Pada jenis permasalahan berbeda, Hansun menggunakan FTS untuk meramalkan pergerakan Indeks Harga Saham Gabungan (IHSG) di Bursa Efek Indonesia. Menggunakan persentase laju perubahan IHSG sebagai himpunan semesta bagi proses fuzzifikasi dengan interval awal sebanyak tujuh, ia memperoleh tingkat keakurasian peramalan in-sample dari FTS sebesar 4,78 persen [3].
Riset ini dimotivasi oleh keinginan untuk mengelaborasi kinerja model FTS dan model Rantai Markov dalam meramalkan secara insample PDRB Provinsi Bali pada periode tahun 1992 hingga 2013. Tingkat akurasi ramalan dari masing-masing model selanjutnya dibandingkan untuk menentukan model yang lebih unggul dalam meramalkan PDRB Provinsi Bali.
Bagian-bagian selanjutnya dari tulisan ini disusun mengikuti format berikut: bagian metode penelitian menguraikan jenis data dan tahapan pengembangan model untuk kedua model yang dielaborasi; bagian hasil dan pembahasan menguraikan secara rinci langkah-langkah pengembangan kedua model, hasil ramalan, serta komparasi keakuratan ramalan kedua model; dan ditutup oleh kesimpulan dan rekomendasi riset.
Sebagai sebuah studi non-experimental, data yang dianalisis merupakan data sekunder dan diperoleh dari BPS Provinsi Bali dalam bentuk data triwulan PDRB Bali adhk tahun 2000 pada periode data yang diramalkan. Mengingat ada dua model yang dikembangkan pada penelitian ini, maka tahapan pengembangan masing-masing model diuraikan terpisah sebagai berikut:
-
A. Tahapan Pengembangan Model FTS
Secara umum model FTS yang dibangun merujuk kepada tahapan yang disarankan oleh [4] dengan memodifikasi penentuan jumlah interval awal. Secara rinci, model FTS dibangun mengikuti tahapan berikut:
-
(a) Menghitung laju perubahan PDRB antardua triwulan yang berturutan. Laju perubahan PDRB (τ∣) dihitung menggunakan pers. (1):
!" ! !"#$
r, =----⅛---— x100
■ !"#$ >>>
(1)
-
(b) Menentukan himpunan semesta U dengan syarat seluruh r∣ menjadi anggotanya. Pada penelitian ini, batas-batas U didefinisikan sebagai:
U = [R!"# - d!; R!"# + d! ] (2)
Pada pers. (2), R!"# dan R!"# adalah nilai-nilai minimum dan maksimum dari r!, dan d! serta d! merupakan dua konstanta sembarang;
-
(c) Membagi U menjadi n buah interval Ui, ..., Un dengan lebar yang sama. Pada penelitian ini nilai n ditentukan menggunakan formula Sturges [5] dalam bentuk pers. (3):
n = 1 + 3,322 log!" (N) (3)
-
(d) Menentukan banyaknya r yang ada pada interval Ui, i = 1, …, n. Selanjutnya, Ui dengan r! terbanyak dibagi menjadi 4 subinterval; Ui dengan r terbanyak kedua dibagi menjadi 3 sub-interval; Ui dengan r terbanyak ketiga dibagi menjadi 2 sub-interval. Interval yang tidak memiliki r! digabungkan dengan interval sebelumnya yang memiliki anggota. Misalkan jumlah interval akhir yang terbentuk f buah, maka F1, …, Ff merupakan himpunan variabel-variabel linguistik dalam himpunan fuzzy IF dengan f1, ., f f menyatakan nilai-nilai linguistik;
-
(e) Melakukan fuzzifikasi nilai-nilai r menjadi nilai-nilai linguistik yang bersesuaian;
-
(f) Melakukan defuzzifikasi variabel linguistik masing-masing amatan sehingga diperoleh nilai r. Defuzzifikasi dilakukan menggunakan fuzzy dengan fungsi keanggotaan segi-tiga (fuzzy triangular number/FTN) yang dapat dinyatakan dalam pers. (4):
! ! ! !
_!_, !,!; j = 1 !
! !
-⅛; 2 ≤j ≤f - 1
!!! !
! ! ! !
TTTT-; j = f
(4)
Pada pers. (4), fj merupakan nilai linguistik dari masing-masing Fj yang besarnya ditentukan sama dengan nilai tengah interval fuzzy Fj;
-
(g) Menduga PDRB pada waktu ke - t menggunakan nilai ri' yang dihitung pada tahap (f) menggunakan pers. (5):
pDRB! = (1 + ft) PDRB!!! (5)
-
(h) Menghitung galat masing-masing ramalan dan nilai AFER menggunakan pers. (6):
! I!"#$ •!! !"#$ ! I
AFER = -------
(6)
-
B. Tahapan Pengembangan Model Markov
Tahapan-tahapan awal peramalan PDRB Bali dengan model Markov Chain mengikuti lima tahapan awal model FTS. Perbedaan metode mulai ada pada tahapan ke-enam sebagai berikut [5]:
-
(f) Menentukan left-hand side (LHS) dan righthand side (RHS) dari masing-masing amatan. LHS dari amatan ke – i merupakan variabel linguistik dari amatan sebelumnya dan RHS-nya merupakan variabel linguistik dari amatan yang bersangkutan;
-
(g) Menentukan Fuzzy Logical Relationship Group (FLRG), sebuah himpunan yang beranggotakan seluruh relasi dari LHS → RHS;
-
(h) Membuat state transition matrix (STM) berukuran f x f yang beranggotakan banyaknya amatan pada FLRG: Fi → Fj ;
-
(i) Menghitung transition probability matrix (TPM) berukuran f x f dengan elemen pada baris ke-i dan kolom ke-j dihitung dari pers. (7):
! ! !
P!,! = (7)
!! ! ! !,!
Pada pers. (7) c!,! menyatakan elemen pada baris ke-i dan kolom ke-j dari STM dan f
menyatakan total variabel linguistik yang terbentuk pada tahap (d);
-
(j) Menghitung η dari masing-masing amatan yang telah terfuzzifikasi menjadi Fi pada tahapan (e) dengan menggunakan pers. (8):
-m∣ ■
fi = [p!,! ■■■ p!,! ] ■■■
m!.
(8)
Pada pers. (8) m! , ..., m! masing-masing menyatakan nilai tengah dari interval-interval fuzzy F1, …, Ff;
-
(k) Menduga nilai ramalan PDRB pada waktu ke-t dengan menggunakan pers. (5);
-
(l) Menghitung nilai galat ramalan dan AFER dari metode Markov Chain menggunakan pers. (6).
Lima tahapan awal aktivitas peramalan PDRB Provinsi Bali menggunakan FTS dan MC sama. Memperhatikan hal ini, maka hasil penelitian diuraikan dengan urutan berikut:
-
A. Penentuan Interval Awal dan Densitas dari
Setiap Interval
Laju perubahan nilai PDRB dari dua triwulan yang berturutan dihitung terlebih dahulu. Jumlah amatan r! adalah 87 data, dengan RMin dan RMax masing-masing bernilai -9,48 persen dan 34,59 persen. Melalui penetapan d1 dan d2 masing-masing sebesar 0,52 persen dan 0,41 persen diperoleh U = [-10,00%; 35,00%] sehingga lebar interval U = 45%. Aplikasi pers. (3) pada penentuan jumlah interval awal memberikan hasil terdapat 8 interval yang harus didefinisikan agar seluruh r! terklasifikasikan. Delapan interval awal dan jumlah amatan yang berada di dalamnya dicantumkan pada Tabel 1:
Tabel 1. Interval Awal Fuzzy dan Kepadatannya
|
Interval |
Batas Kiri |
Batas Kanan |
Frekuensi Data |
|
U1 |
-10,00% |
-4,38% |
1 |
|
U2 |
-4,38% |
1,25% |
20 |
|
U3 |
1,25% |
6,88% |
57 |
|
U4 |
6,88% |
12,50% |
6 |
|
U5 |
12,50% |
18,13% |
1 |
|
U6 |
18,13% |
23,75% |
0 |
|
U7 |
23,75% |
29,38% |
1 |
|
U8 |
29,38% |
35,00% |
1 |
Sumber: Analisis Data (2014)
-
B. Penentuan Interval Akhir dan Densitas dari
Setiap Interval
Merujuk kepada tahapan yang disarankan oleh [4] dengan memodifikasi penentuan jumlah interval awal], maka U3, U2, dan U4 sebagai interval-interval dengan frekuensi data tertinggi harus dipecah menjadi sub-sub interval masing-masing berjumlah 4, 3, dan 2 sub interval. Sebaliknya, U6 dengan nilai densitas 0 digabungkan dengan U5. Tabel 2 menunjukkan interval akhir yang terbentuk mengikuti kriteria tersebut:
Tabel 2. Interval Akhir Fuzzy dan Nilai Linguistik
|
Interval Fuzzy |
Minimum |
Nilai Tengah |
Maksimum |
Nilai Linguistik |
|
F1 |
-10.00% |
-7.19% |
-4.38% |
f1 |
|
F2 |
-4.38% |
-3.44% |
-2.50% |
f2 |
|
F3 |
-2.50% |
-1.56% |
-0.63% |
f3 |
|
F4 |
-0.63% |
0.31% |
1.25% |
f4 |
|
F5 |
1.25% |
1.95% |
2.66% |
f5 |
|
F6 |
2.66% |
3.36% |
4.06% |
f6 |
|
F7 |
4.06% |
4.77% |
5.47% |
f7 |
|
F8 |
5.47% |
6.17% |
6.88% |
f8 |
|
F9 |
6.88% |
8.28% |
9.69% |
f9 |
|
F10 |
9.69% |
11.09% |
12.50% |
f10 |
|
F11 |
12.50% |
18.13% |
23.75% |
f11 |
|
F12 |
23.75% |
26.56% |
29.38% |
f12 |
|
F13 |
29.38% |
32.19% |
35.00% |
f13 |
|
Sumber: Analisis Data (2014) | ||||
C. Fuzzifikasi dan Proses Peramalan FTS
Informasi pada Tabel 2 selanjutnya digunakan untuk melakukan fuzzifikasi masing-masing r! dengan hasil akhir fuzzifikasi tercantum pada lampiran 2. Mengacu kepada representasi fuzzy masing-masing r!, maka menggunakan pers. (4), nilai r! diduga. Sebagai contoh, laju perubahan PDRB pada triwulan III tahun 1992 dengan nilai sebesar 3,05 persen terfuzzifikasi ke dalam variabel linguistik F6. Menggunakan pers. (4) nilai ini diramalkan sebesar:
0,5 + 1 + 0,5
^ = F!
0,5 1 0,5
fi + fi + fi
2
0,5 1 0,5
1,95% + 3,36% + 4,77% = 3,04%
Nilai ramalan r! untuk triwulan lainnya selengkapnya dapat diacu pada lampiran.
D. Penghitungan AFER dari Model FTS
Nilai AFER dari ramalan dengan menggunakan model FTS diperoleh dengan terlebih dulu menduga nilai PDRB dari masing-masing amatan melalui aplikasi pers. (5). Penghitungan akhir menunjukkan AFER peramalan dari model FTS secara in-sample pada data PDRB Provinsi Bali sebesar 0,78 persen. Penghitungan selengkapnya dicantumkan pada lampiran.
E. Peramalan dengan Model Rantai Markov
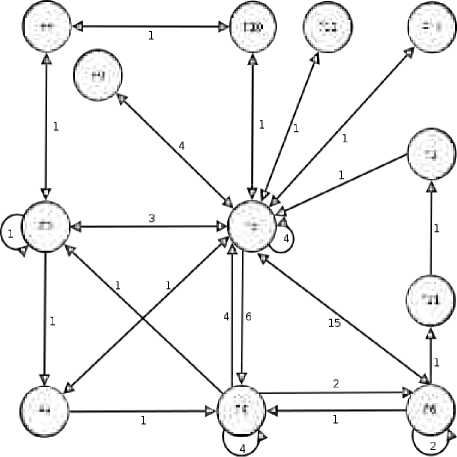
Model kedua yang digunakan meramalkan data PDRB Provinsi Bali adalah model Rantai Markov (Markov Chain/MC model). Peramalan diawali dengan membangun FLRG dari representasi fuzzy masing-masing nilai r!. FLRG selengkapnya dicantumkan pada lampiran. Merujuk kepada FLRG yang terbentuk, dibangun state transition diagram seperti gambar 1 dengan STM ditunjukkan di bawahnya:
Pada gambar 1, awal dan akhir dari simbol-simbol panah merupakan LHS dan RHS dari FLRG yang terbentuk dan angka-angka menunjukkan jumlah dari LHS → RHS pada masing-masing relasi. Mengacu kepada gambar 1, maka STM disusun dengan baris dan kolom merupakan representasi dari LHS dan RHS. Pada STM, unsur yang kosong menunjukkan tidak ada amatan dengan LHS menuju RHS yang bersesuaian.
Mengacu kepada STM yang dibangun, maka perlu disusun matriks peluang transisi (TPM) Markov yang digunakan untuk menduga nilai r!. Berikut adalah TPM yang disusun dari STM sebelumnya:
F1 F2 F3
F1
F2 1 1
66
F3
Gambar 1. Diagram Transisi Markov
TPM =
⎝
F1 F2 F3 F4
STM =
F1
F2
F3
F4
F5
F6
F8
11
1
14
316
1
1
⎜⎜ F9
⎜ F10
⎜ F11
⎜⎜ F12
⎜ F13 ⎝
1
F4
F5
F6
F8
F9
F10
F11
F12
F13
1
11
12 36
F4 F5 F6 F8 F9 F10 F11 F12 F13
1
11
26
11
22
442
1
2
1
11
1
1
⎠
Nilai pada elemen-elemen TPM selanjutnya
digunakan untuk menduga nilai r! setiap amatan sesuai dengan FLRG-nya. Sebagai contoh, laju perubahan PDRB pada triwulan III tahun 1992 dengan nilai sebesar 3,05 persen diduga dengan mengamati bahwa nilai LHS dari amatan ini adalah F5. Pada TPM terlihat ada sembilan kemungkinan state RHS bila LHS = F5, masing-masing dengan peluang yang berbeda. Nilai r! pada amatan ini selanjutnya bisa diduga sebagai jumlah hasil perkalian (sumproduct) dari peluang state berikutnya bila LHS = F5 dengan nilai-nilai tengah dari seluruh interval fuzzy (lihat pers. 8),
sebagai berikut:
r!
0
1
36
-7,19%∖
= 4,20%
32,19%
Nilai penduga yang diperoleh selanjutnya digunakan untuk menduga nilai PDRB dari periode yang diramalkan. Menggunakan pers. (5) diperoleh nilai PDRB triwulan III tahun 1992 sebesar 1020439 juta rupiah, dengan persentase galat sebesar 1,12 persen.
Nilai AFER model Rantai Markov diperoleh dengan menghitung rataan seluruh galat amatan (perhitungan lengkap pada lampiran) sebesar 2,74 persen; lebih besar dari nilai AFER yang
diperoleh menggunakan metode FTS. Gambar 2 memperlihatkan histogram data PDRB, dan data hasil ramalan menggunakan kedua model:
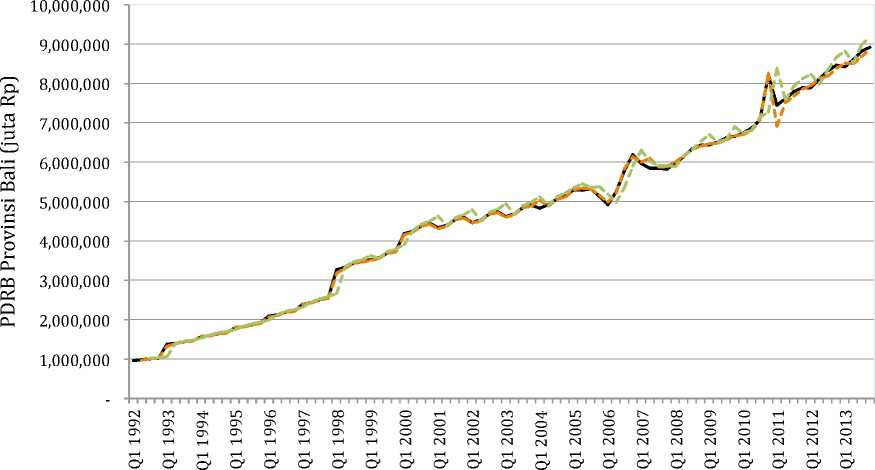
PDRB Model FTS Model MC
Gambar 2. Grafik Komparasi Data Asli dengan Hasil Peramalan Model FTS dan MC
-
A. Simpulan Penelitian
Penelitian yang ditujukan untuk mengetahui kinerja model FTS dan Rantai Markov dalam meramalkan PDRB Provinsi Bali pada periode tahun 1992 – 2013 atas dasar harga konstan tahun 2000 menyimpulkan:
-
1. Kedua model menghasilkan ramalan yang baik ditinjau dari nilai rataan persentase galat (AFER) di bawah lima persen. Nilai-nilai AFER pada model FTS dan Rantai Markov masing-masing sebesar 0,78 persen dan 2,74 persen;
-
2. Melalui perbandingan kedua nilai AFER tersebut, model FTS dengan AFER yang lebih kecil memiliki tingkat keakurasian ramalan yang lebih baik dibandingkan dengan model Rantai Markov.
-
B. Rekomendasi
Meskipun kedua model memberikan nilai-nilai ramalan dengan batas galat yang masih bisa
diterima, beberapa hal direkomendasikan terkait dengan hasil penelitian:
-
1. Nilai-nilai AFER diperoleh terbatas pada peramalan yang bersifat in-sample. Mengacu kepada hal ini, disarankan untuk memeriksa nilai PDRB Provinsi Bali pada tahun 2014 sehingga AFER untuk peramalan yang bersifat out-of-sample bisa dihitung;
-
2. Disarankan untuk melakukan pemeriksaan pencilan, sebelum dilakukan proses peramalan menggunakan kedua model;
-
3. Disarankan mencoba parameter-parameter yang berbeda dari fungsi keanggotaan segi-tiga yang digunakan saat defuzzifikasi.
DAFTAR PUSTAKA
-
[1] BPS Provinsi Bali, 2013. Produk Domestik Regional Bruto (PDRB) Provinsi Bali 2008 – 2012. Denpasar: Badan Pusat Statistik Provinsi Bali.
-
[2] Wanayasa, IGN. Arya., Kencana, I Putu EN. & Nilakusmawati, D.P.E., “Peramalan Produk Domestik Regional Bruto (PDRB) Provinsi
Bali dengan Menggunakan Metode Fuzzy Time Series”, E-Jurnal UNUD, 1(1), pp.1219, 2012
-
[3] Seng Hansun, "Peramalan Data IHSG Menggunakan Fuzzy Time Series," IJCCS, vol. 6 (2), pp. 79-88, 2012.
-
[4] Meredith Stevenson and John E. Porter, "Fuzzy Time Series Forecasting Using Percentage Change as the Universe of Discour-
se," World Academy of Science, Engineering and Technology, vol. 55, pp. 154-157, 2009.
-
[5] R. C. Tsaur, “A Fuzzy Time Series-Markov Chain Model With An Application To Forecast the Exchange Rate Between The Taiwan And US Dollar”, International Journal of Innovative Computing, Information and Control, Volume 8, pp. 4931-42, 2012.
LAMPIRAN
Lampiran. Data PDRB Bali 1992 – 2013 adhk Tahun 2000 (Juta Rp) dan Parameter-parameter pada Model FTS dan Rantai Markov
|
Periode |
PDRB |
rt |
Model FTS |
Model Markov | |||||
|
υ |
PDRB! |
% Galat |
FLRG |
r? |
PDRB! |
% Galat | |||
|
Q1 – 1992 |
963 504 | ||||||||
|
Q2 – 1992 |
979 315 |
1.64% |
0.88% |
972 027 |
0.74% | ||||
|
Q3 – 1992 |
1 009 142 |
3.05% |
3.04% |
1 009 055 |
0.01% |
F5 → F6 |
4.20% |
1 020 439 |
1.12% |
|
Q4 – 1992 |
1 024 441 |
1.52% |
0.88% |
1 018 069 |
0.62% |
F6 → F5 |
2.87% |
1 038 064 |
1.33% |
|
Q1 – 1993 |
1 378 770 |
34.59% |
30.07% |
1 332 442 |
3.36% |
F5 → F13 |
4.20% |
1 067 460 |
22.58% |
|
Q2 – 1993 |
1 401 395 |
1.64% |
0.88% |
1 390 967 |
0.74% |
F13 → F5 |
1.95% |
1 405 699 |
0.31% |
|
Q3 – 1993 |
1 444 078 |
3.05% |
3.04% |
1 443 952 |
0.01% |
F5 → F6 |
4.20% |
1 460 243 |
1.12% |
|
Q4 – 1993 |
1 465 970 |
1.52% |
0.88% |
1 456 853 |
0.62% |
F6 → F5 |
2.87% |
1 485 465 |
1.33% |
|
Q1 – 1994 |
1 572 696 |
7.28% |
8.10% |
1 584 750 |
0.77% |
F5 → F9 |
4.20% |
1 527 529 |
2.87% |
|
Q2 – 1994 |
1 598 504 |
1.64% |
0.88% |
1 586 609 |
0.74% |
F9 → F5 |
1.95% |
1 603 413 |
0.31% |
|
Q3 – 1994 |
1 647 190 |
3.05% |
3.04% |
1 647 047 |
0.01% |
F5 → F6 |
4.20% |
1 665 629 |
1.12% |
|
Q4 – 1994 |
1 672 161 |
1.52% |
0.88% |
1 661 762 |
0.62% |
F6 → F5 |
2.87% |
1 694 398 |
1.33% |
|
Q1 – 1995 |
1 795 382 |
7.37% |
8.10% |
1 807 648 |
0.68% |
F5 → F9 |
4.20% |
1 742 379 |
2.95% |
|
Q2 – 1995 |
1 824 843 |
1.64% |
0.88% |
1 811 264 |
0.74% |
F9 → F5 |
1.95% |
1 830 448 |
0.31% |
|
Q3 – 1995 |
1 880 423 |
3.05% |
3.04% |
1 880 259 |
0.01% |
F5 → F6 |
4.20% |
1 901 472 |
1.12% |
|
Q4 – 1995 |
1 908 931 |
1.52% |
0.88% |
1 897 058 |
0.62% |
F6 → F5 |
2.87% |
1 934 315 |
1.33% |
|
Q1 – 1996 |
2 089 027 |
9.43% |
8.10% |
2 063 602 |
1.22% |
F5 → F9 |
4.20% |
1 989 091 |
4.78% |
|
Q2 – 1996 |
2 123 307 |
1.64% |
0.88% |
2 107 507 |
0.74% |
F9 → F5 |
1.95% |
2 129 828 |
0.31% |
|
Q3 – 1996 |
2 187 977 |
3.05% |
3.04% |
2 187 787 |
0.01% |
F5 → F6 |
4.20% |
2 212 469 |
1.12% |
|
Q4 – 1996 |
2 221 147 |
1.52% |
0.88% |
2 207 332 |
0.62% |
F6 → F5 |
2.87% |
2 250 683 |
1.33% |
|
Q1 – 1997 |
2 398 197 |
7.97% |
8.10% |
2 401 115 |
0.12% |
F5 → F9 |
4.20% |
2 314 418 |
3.49% |
|
Q2 – 1997 |
2 437 550 |
1.64% |
0.88% |
2 419 412 |
0.74% |
F9 → F5 |
1.95% |
2 445 037 |
0.31% |
|
Q3 – 1997 |
2 511 791 |
3.05% |
3.04% |
2 511 573 |
0.01% |
F5 → F6 |
4.20% |
2 539 908 |
1.12% |
|
Q4 – 1997 |
2 549 870 |
1.52% |
0.88% |
2 534 011 |
0.62% |
F6 → F5 |
2.87% |
2 583 778 |
1.33% |
|
Q1 – 1998 |
3 277 421 |
28.53% |
24.76% |
3 181 282 |
2.93% |
F5 → F12 |
4.20% |
2 656 945 |
18.93% |
|
Q2 – 1998 |
3 331 202 |
1.64% |
0.88% |
3 306 414 |
0.74% |
F12 → F5 |
1.95% |
3 341 433 |
0.31% |
|
Q3 – 1998 |
3 432 661 |
3.05% |
3.04% |
3 432 363 |
0.01% |
F5 → F6 |
4.20% |
3 471 086 |
1.12% |
|
Q4 – 1998 |
3 484 701 |
1.52% |
0.88% |
3 463 027 |
0.62% |
F6 → F5 |
2.87% |
3 531 039 |
1.33% |
|
Q1 – 1999 |
3 520 936 |
1.04% |
0.64% |
3 506 925 |
0.40% |
F5 → F4 |
4.20% |
3 631 031 |
3.13% |
|
Q2 – 1999 |
3 578 713 |
1.64% |
0.88% |
3 552 083 |
0.74% |
F4 → F5 |
1.12% |
3 560 447 |
0.51% |
|
Q3 – 1999 |
3 687 711 |
3.05% |
3.04% |
3 687 391 |
0.01% |
F5 → F6 |
4.20% |
3 728 991 |
1.12% |
|
Q4 – 1999 |
3 743 617 |
1.52% |
0.88% |
3 720 334 |
0.62% |
F6 → F5 |
2.87% |
3 793 399 |
1.33% |
|
Q1 – 2000 |
4 184 187 |
11.77% |
11.23% |
4 164 002 |
0.48% |
F5 → F10 |
4.20% |
3 900 820 |
6.77% |
|
Q2 – 2000 |
4 252 848 |
1.64% |
0.88% |
4 221 201 |
0.74% |
F10 → F5 |
1.95% |
4 265 909 |
0.31% |
|
Q3 – 2000 |
4 382 378 |
3.05% |
3.04% |
4 381 998 |
0.01% |
F5 → F6 |
4.20% |
4 431 434 |
1.12% |
|
Q4 – 2000 |
4 448 816 |
1.52% |
0.88% |
4 421 146 |
0.62% |
F6 → F5 |
2.87% |
4 507 975 |
1.33% |
|
Q1 – 2001 |
4 332 393 |
-2.62% |
-2.94% |
4 318 060 |
0.33% |
F5 → F2 |
4.20% |
4 635 632 |
7.00% |
|
Q2 – 2001 |
4 403 485 |
1.64% |
0.88% |
4 370 719 |
0.74% |
F2 → F5 |
1.17% |
4 383 163 |
0.46% |
|
Q3 – 2001 |
4 537 603 |
3.05% |
3.04% |
4 537 209 |
0.01% |
F5 → F6 |
4.20% |
4 588 397 |
1.12% |
|
Q4 – 2001 |
4 606 394 |
1.52% |
0.88% |
4 577 744 |
0.62% |
F6 → F5 |
2.87% |
4 667 649 |
1.33% |
|
Periode |
PDRB |
rt |
Model FTS |
Model Markov | |||||
|
fi |
PDRB! |
% Galat |
FLRG |
PDRB! |
% Galat | ||||
|
Q1 – 2002 |
4 464 203 |
-3.09% |
-2.94% |
4 471 006 |
0.15% |
U5 → U2 |
4.20% |
4 799 827 |
7.52% |
|
Q2 – 2002 |
4 537 459 |
1.64% |
0.88% |
4 503 695 |
0.74% |
U2 → U5 |
1.17% |
4 516 518 |
0.46% |
|
Q3 – 2002 |
4 675 658 |
3.05% |
3.04% |
4 675 252 |
0.01% |
U5 → U6 |
4.20% |
4 727 997 |
1.12% |
|
Q4 – 2002 |
4 746 541 |
1.52% |
0.88% |
4 717 020 |
0.62% |
U6 → U5 |
2.87% |
4 809 660 |
1.33% |
|
Q1 – 2003 |
4 623 407 |
-2.59% |
-2.94% |
4 607 034 |
0.35% |
U5 → U2 |
4.20% |
4 945 859 |
6.97% |
|
Q2 – 2003 |
4 699 274 |
1.64% |
0.88% |
4 664 307 |
0.74% |
U2 → U5 |
1.17% |
4 677 588 |
0.46% |
|
Q3 – 2003 |
4 842 402 |
3.05% |
3.04% |
4 841 981 |
0.01% |
U5 → U6 |
4.20% |
4 896 607 |
1.12% |
|
Q4 – 2003 |
4 915 813 |
1.52% |
0.88% |
4 885 239 |
0.62% |
U6 → U5 |
2.87% |
4 981 183 |
1.33% |
|
Q1 – 2004 |
4 837 204 |
-1.60% |
2.46% |
5 036 514 |
4.12% |
U5 → U3 |
4.20% |
5 122 239 |
5.89% |
|
Q2 – 2004 |
4 916 580 |
1.64% |
0.88% |
4 879 995 |
0.74% |
U3 → U5 |
1.13% |
4 892 000 |
0.50% |
|
Q3 – 2004 |
5 066 326 |
3.05% |
3.04% |
5 065 886 |
0.01% |
U5 → U6 |
4.20% |
5 123 038 |
1.12% |
|
Q4 – 2004 |
5 143 133 |
1.52% |
0.88% |
5 111 144 |
0.62% |
U6 → U5 |
2.87% |
5 211 525 |
1.33% |
|
Q1 – 2005 |
5 301 871 |
3.09% |
3.04% |
5 299 319 |
0.05% |
U5 → U6 |
4.20% |
5 359 104 |
1.08% |
|
Q2 – 2005 |
5 289 872 |
-0.23% |
0.64% |
5 335 684 |
0.87% |
U6 → U4 |
2.87% |
5 453 820 |
3.10% |
|
Q3 – 2005 |
5 325 780 |
0.68% |
0.64% |
5 323 608 |
0.04% |
U4 → U4 |
1.12% |
5 349 233 |
0.44% |
|
Q4 – 2005 |
5 134 990 |
-3.58% |
-2.94% |
5 169 249 |
0.67% |
U4 → U2 |
1.12% |
5 385 544 |
4.88% |
|
Q1 – 2006 |
4 928 053 |
-4.03% |
-2.94% |
4 984 066 |
1.14% |
U2 → U2 |
1.17% |
5 195 166 |
5.42% |
|
Q2 – 2006 |
5 249 667 |
6.53% |
6.11% |
5 229 168 |
0.39% |
U2 → U8 |
1.17% |
4 985 804 |
5.03% |
|
Q3 – 2006 |
5 791 603 |
10.32% |
11.23% |
5 839 171 |
0.82% |
U8 → U10 |
1.95% |
5 352 200 |
7.59% |
|
Q4 – 2006 |
6 189 001 |
6.86% |
6.11% |
6 145 482 |
0.70% |
U10 → U8 |
1.95% |
5 904 720 |
4.59% |
|
Q1 – 2007 |
5 960 000 |
-3.70% |
-2.94% |
6 007 098 |
0.79% |
U8 → U2 |
1.95% |
6 309 880 |
5.87% |
|
Q2 – 2007 |
5 850 000 |
-1.85% |
2.46% |
6 106 339 |
4.38% |
U2 → U3 |
1.17% |
6 029 844 |
3.07% |
|
Q3 – 2007 |
5 850 000 |
0.00% |
0.64% |
5 887 309 |
0.64% |
U3 → U4 |
1.13% |
5 916 270 |
1.13% |
|
Q4 – 2007 |
5 820 000 |
-0.51% |
0.64% |
5 887 309 |
1.16% |
U4 → U4 |
1.12% |
5 915 646 |
1.64% |
|
Q1 – 2008 |
5 980 000 |
2.75% |
3.04% |
5 996 741 |
0.28% |
U4 → U6 |
1.12% |
5 885 310 |
1.58% |
|
Q2 – 2008 |
6 140 000 |
2.68% |
3.04% |
6 161 599 |
0.35% |
U6 → U6 |
2.87% |
6 151 384 |
0.19% |
|
Q3 – 2008 |
6 350 000 |
3.42% |
3.04% |
6 326 458 |
0.37% |
U6 → U6 |
2.87% |
6 315 970 |
0.54% |
|
Q4 – 2008 |
6 430 000 |
1.26% |
0.88% |
6 406 174 |
0.37% |
U6 → U5 |
2.87% |
6 531 988 |
1.59% |
|
Q1 – 2009 |
6 440 000 |
0.16% |
0.64% |
6 471 008 |
0.48% |
U5 → U4 |
4.20% |
6 700 010 |
4.04% |
|
Q2 – 2009 |
6 510 000 |
1.09% |
0.64% |
6 481 071 |
0.44% |
U4 → U4 |
1.12% |
6 512 267 |
0.03% |
|
Q3 – 2009 |
6 630 000 |
1.84% |
0.88% |
6 567 589 |
0.94% |
U4 → U5 |
1.12% |
6 583 053 |
0.71% |
|
Q4 – 2009 |
6 660 000 |
0.45% |
0.64% |
6 672 283 |
0.18% |
U5 → U4 |
4.20% |
6 908 408 |
3.73% |
|
Q1 – 2010 |
6 740 000 |
1.20% |
0.64% |
6 702 474 |
0.56% |
U4 → U4 |
1.12% |
6 734 736 |
0.08% |
|
Q2 – 2010 |
6 860 000 |
1.78% |
0.88% |
6 799 624 |
0.88% |
U4 → U5 |
1.12% |
6 815 634 |
0.65% |
|
Q3 – 2010 |
7 070 000 |
3.06% |
3.04% |
7 068 323 |
0.02% |
U5 → U6 |
4.20% |
7 148 066 |
1.10% |
|
Q4 – 2010 |
8 230 000 |
16.41% |
16.80% |
8 257 573 |
0.34% |
U6 → U11 |
2.87% |
7 272 623 |
11.63% |
|
Q1 – 2011 |
7 450 000 |
-9.48% |
-15.95% |
6 917 540 |
7.15% |
U11 → U1 |
1.95% |
8 390 742 |
12.63% |
|
Q2 – 2011 |
7 610 000 |
2.15% |
0.88% |
7 515 905 |
1.24% |
U1 → U5 |
1.95% |
7 595 508 |
0.19% |
|
Q3 – 2011 |
7 790 000 |
2.37% |
0.88% |
7 677 320 |
1.45% |
U5 → U5 |
4.20% |
7 929 561 |
1.79% |
|
Q4 – 2011 |
7 900 000 |
1.41% |
0.88% |
7 858 913 |
0.52% |
U5 → U5 |
4.20% |
8 117 119 |
2.75% |
|
Q1 – 2012 |
7 900 000 |
0.00% |
0.64% |
7 950 383 |
0.64% |
U5 → U4 |
4.20% |
8 231 738 |
4.20% |
|
Q2 – 2012 |
8 120 000 |
2.78% |
3.04% |
8 139 906 |
0.25% |
U4 → U6 |
1.12% |
7 988 651 |
1.62% |
|
Q3 – 2012 |
8 320 000 |
2.46% |
0.88% |
8 191 832 |
1.54% |
U6 → U5 |
2.87% |
8 352 715 |
0.39% |
|
Q4 – 2012 |
8 460 000 |
1.68% |
0.88% |
8 393 601 |
0.78% |
U5 → U5 |
4.20% |
8 669 375 |
2.47% |
|
Q1 – 2013 |
8 430 000 |
-0.35% |
0.64% |
8 513 954 |
1.00% |
U5 → U4 |
4.20% |
8 815 254 |
4.57% |
|
Q2 – 2013 |
8 610 000 |
2.14% |
0.88% |
8 504 574 |
1.22% |
U4 → U5 |
1.12% |
8 524 598 |
0.99% |
|
Q3 – 2013 |
8 820 000 |
2.44% |
0.88% |
8 686 166 |
1.52% |
U5 → U5 |
4.20% |
8 971 553 |
1.72% |
|
Q4 – 2013 |
8 920 000 |
1.13% |
0.64% |
8 876 250 |
0.49% |
U5 → U4 |
4.20% |
9 190 371 |
3.03% |
|
AFER |
0.78% |
2.74% | |||||||
122
Discussion and feedback