PERAMALAN VOLATILITAS RETURN NILAI TUKAR RUPIAH TERHADAP US DOLLAR MENGGUNAKAN METODE EGARCH, TGARCH, DAN APARCH
on
E-Jurnal Matematika Vol. 13(1), Januari 2024, pp. 82-88
DOI: https://doi.org/10.24843/MTK.2024.v13.i01.p445
ISSN: 2303-1751
PERAMALAN VOLATILITAS RETURN NILAI TUKAR RUPIAH TERHADAP US DOLLAR MENGGUNAKAN METODE EGARCH, TGARCH, DAN APARCH
Made Nonik Pramesti Karana1§, I Wayan Sumarjaya2, Kartika Sari3
1Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email: nonikpramsti23ixh@gmail.com]
-
2Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email: sumarjaya@unud.ac.id]
-
3Program Studi Matematika, Fakultas MIPA-Universitas Udayana [Email: sarikartika@unud.ac.id] §Corresponding Author
ABSTRACT
Exchange rates play a crucial role among macroeconomic variables, exerting a significant influence on a country's economic landscape. Fluctuations in these rates can impact a nation's stability and economic activities. Consequently, it becomes essential to engage in forecasting endeavors, particularly in predicting the exchange rate of the rupiah against foreign currencies, with a focus on the US dollar. Certain instances in financial data reveal an asymmetric volatility response, often referred to as the leverage effect. To address this challenge, asymmetric GARCH models, including EGARCH, TGARCH, and APARCH, prove instrumental. This research endeavors to identify the most effective model among EGARCH, TGARCH, and APARCH using data pertaining to the rupiah's exchange rate against the US Dollar from March 2, 2020, to June 2, 2022. The findings indicate that the APARCH (1,2) model stands out as the optimal choice for predicting volatility, boasting the smallest AIC value in comparison to its counterparts. As per the research outcomes, volatility witnessed a decline from the initial day to the fourteenth day.
Keywords: GARCH, EGARCH, TGARCH, APARCH, Volatility
Nilai tukar merupakan salah satu bagian dari variabel makroekonomi yang berperan penting terhadap perekonomian suatu negara karena perubahan nilai tukar dapat memengaruhi stabilitas dan kegiatan ekonomi suatu negara (Firman, 2020).
Data nilai tukar setiap waktunya dapat berubah-ubah atau cenderung tidak konstan tergantung dengan kondisi saat terjadi perubahan terhadap nilai tukar itu sendiri (Laila, 2018). Kecenderungan peningkatan inflasi di Indonesia, misalnya, merupakan dampak langsung dari melemahnya nilai rupiah dibandingkan dollar. Hal ini menjadi contoh bagaimana fluktuasi nilai tukar dapat berdampak pada perekonomian suatu negara. (Elvitra et al., 2013). Fluktuasi nilai tukar dipengaruhi oleh beberapa faktor, khususnya biaya pinjaman, peningkatan nilai tukar, dan tingkat pertumbuhan ekonomi. Fluktuasi nilai tukar merupakan sumber risiko bagi para investor, organisasi, dan bank di bursa global (Dewi, 2012). Oleh karena itu, peramalan perlu dilakukan dengan tujuan untuk memprediksi
nilai tukar rupiah terhadap mata uang lain, seperti US dollar. Menurut Bau et al., (2016) pemantauan nilai tukar rupiah terhadap US dollar harus dilakukan untuk memastikan perekonomian negara tetap stabil atau tidak.
Karena volatilitas data nilai tukar biasanya tidak konstan, varians sisa merupakan ukuran dinamis dari fluktuasi ini. Menurut Tsay (2005), volatilitas dapat memberikan perbedaan kenaikan atau penurunan yang disebut sebagai keasimetrisan (leverage effect), di mana pada data terdapat perbedaan dalam besarnya perubahan volatilitas saat nilai bergerak (heteroskedastisitas) pada data.
Permasalahan heteroskedastisitas bisa ditangani dengan model ARCH/GARCH. Engle mempresentasikan model autoregressive conditional heteroskedasticity (ARCH) pada tahun 1982 yang digunakan untuk mengatasi heterogenitas varians dengan memodelkan mean dan varians secara bersamaan (Tsay, 2005). Namun, model ini dipandang kurang efektif jika diterapkan pada data keuangan yang memiliki
volatilitas yang tinggi, karena membutuhkan tingkat orde yang tinggi dalam memodelkan variansnya, hal ini menyulitkan tahapan identifikasi dan estimasi model (Untari et al., 2009). Tahun 1986, Bollerslev mengembangkan model ARCH jadi generalized autoregressive
conditional heteroscedasticity (GARCH)
(Tsay,2005). Model ARCH dan GARCH
menunjukkan volatilitas yang simetris atau
disesuaikan kepada berbagai kemungkinan dan guncangan, lebih spesifiknya, guncangan berita yang baik dan berita buruk (Elvitra et al., 2013).
Kekurangan model ARCH/GARCH ini bisa diatasi dengan memakai model GARCH asimetris (Tsay, 2005). Model EGARCH (exponentian GARCH) yang diusulkan oleh Nelson pada tahun 1991. TGARCH (threshold GARCH) yang dikemukakan oleh Zakoian pada tahun 1994. Sementara itu, APARCH (assymetric power ARCH) yang diusulkan oleh Ding, Granger, dan Engle pada tahun 1993.
Berdasarkan uraian pada bagian terdahulu, tujuan dari penelitian ini yaitu mengetahui hasil peramalan volatilitas return nilai tukar mata uang rupiah terhadap US dollar berdasarkan model terbaik di antara model EGARCH, TGARCH, dan APARCH.
Untuk keperluan penelitian ini digunakan data sekunder yang diperoleh dari situs resmi Bank Indonesia yang dapat dilihat di www.bi.go.id. Data yang digunakan data kurs jual rupiah terhadap US dollar pada tanggal 2 Maret 2020 hingga tanggal 2 Juni 2022, yang merupakan jangka waktu pengamatan data. Jumlah pengamatan adalah 559 hari selama hari kerja sesuai ketentuan Bank Indonesia.
Adapun langkah-langkah analisis data yaitu:
-
1. Menghitung data return memakai persamaan:
-
rt = ln(lJ) (1)
dengan Pt adalah harga aset pada waktu ke-1 dan ln ialah logaritma natural.
-
2. Menghitung mean, standar deviasi, skewness, dan kurtosis untuk melihat gambaran dari data return.
-
3. Memeriksa kestasioneran data return melalui plot data, grafik korelogram ACF dan PACF. Selain itu penggunaan uji ADF dengan hipotesis:
H0∙.β = 0 (ditemukan unit root ataupun data tidak stasioner)
H1: β <0 (tidak ditemukan unit root ataupun data stasioner)
Statistik uji yang diterapkan dalam uji ADF:
1-1 SE(β)
ADF =
(2)
dengan SE(β) adalah nilai standar error dari
estimasi β. Daerah kritis: hipotesis H0 ditolak apabila p — value < a, yang menunjukkan yaitu data stasioner (Tsay, 2005). Jika data return tidak stasioner bisa dilakukan
differencing.
-
4. Pengecekan kepada residual kuadrat yang mencakup:
-
a. Melakukan pengujian korelasi untuk melihat ada tidaknya autokorelasi dengan uji Ljung-Box dengan hipotesis:
Ho'∙ Pi = P2 = ∙∙∙ = Pi = O (tidak terdapat autokorelasi)
H1 : terdapat ph≠ 0 untuk h = 1,2,..., l (terdapat autokorelasi)
Statistik uji yang diterapkan:
2
QU, TU ■ 2>∑- — (3)
dengan l sebagai jumlah lag yang diuji dan ph sebagai nilai autokorelasi pada lag h. Daerah kritis: hipotesis H0 ditolak apabila Q(J) > Xa atau ketika p — value < a (Tsay, 2005).
-
b. Menguji efek ARCH dengan menerapkan uji ARCH-LM guna menilai apakah
ditemukan efek ARCH ataupun tidak, hipotesisnya:
Ho : α1 = a2 = a3 = ... = am= 0 (tidak
ditemukan efek ARCH)
Hi : terdapat αi ≠ 0,i = 1,2,3,..., m (ada efek ARCH)
Statistik uji yang diterapkan dalam uji ARCH-LM yaitu:
= (SSR2-SSil)M (4)
DJfil N-2m-1
dengan SSR0 = ∑t=m+1(a2 — ω)2, ω = ∑n a2
t=1 t yang merupakan nilai mean dari at, SSRi = ∑V=m+1⅛ dengan et berikut adalah residual kuadrat terkecil pada waktu t, m adalah derajat bebas, dan N adalah banyak pengujian. Daerah kritis adalah tolak H0 apabila nilai LM > χm (a') atau p -value < α.
Ketika tidak ditemukan korelasi dan tidak ditemukan efek ARCH, maka proses yang sebelumnya tidak akan dilanjutkan. Sebaliknya, ketika ditemukan korelasi dan
ditemukan efek ARCH, maka bisa dilanjutkan pada langkah selanjutnya yaitu langkah 5.
-
5. Memakai maximum likelihood estimation
untuk dilakukan estimasi parameter model GARCH.
-
6. Penentuan model GARCH terbaik dengan melihat nilai AIC terkecil memakai
persamaan berikut:
AIC = -2l + 2k (5)
-
7. Melakukan uji efek asimetris dengan uji sign dan size bias pada model GARCH dengan hipotesis:
H0 :φ1 = φ2 = ■” = φm = 0 (residual
sifatnya simetris)
H1 :terdapat φi ≠ 0;i =
-
1,2, ..., m (residual sifatnya asimetris) Statistik uji yang dipakai yakin:
ssRo/
F= k (6)
SSR1
Daerah kritis adalah tolak H0 jika F > Xm(O) atau P — value < a. Jika efek asimetris pada data tidak ada, model GARCH bisa digunakan untuk peramalan. Pengujian hanya akan dilanjutkan ke langkah selanjutnya (langkah 8) apabila ditemukan adanya efek asimetris.
-
8. Melakukan estimasi parameter untuk model EGARCH, TGARCH, dan APARCH mempergunakan metode maximum
likelihood estimation. Persamaan model
EGARCH yaitu:
ln σ^ = α0 + ∑m=1 ai l⅛=4Zl⅛-l +
∑si=ιβjln(σ2-i) (7)
dengan notasi γι merupakan efek asimetris dari γi merupakan efek asimetris dari at-i.
Persamaan model TGARCH yaitu:
∑m
(aiaθi + γiNt--iat-i)
i=i
+ ∑sj=ιβrf-j
(8)
dengan N— adalah indikator dari at-i negatif atau variabel dummy yang memiliki nilai 1 ketika at-i< 0 dan 0 ketika at-i ≥ 0. Kemudian, model APARCH yaitu:
°t = ao+ ∑,= i al(∖al-i∖ + γiat-ι)δ + ∑‰βiσt-j (9)
dengan γi merupakan efek asimetris antara volatilitas dan return ketika γ ≠ 0, dan δ
9.
merupakan pangkat volatilitas ketika δ ≠ 1.
Penentuan model yang mempunyai nilai AIC terkecil untuk model terbaik dari model
EGARCH, TGARCH, dan APARCH.
-
10. Melakukan peramalan volatilitas data dengan model yang terpilih untuk empat belas hari ke depan yaitu 3 Juni 2022 sampai dengan 16 Juni 2022.
-
3. HASIL DAN PEMBAHASAN
-
3.1 Return
-
Mengacu kepada data kurs jual nilai tukar rupiah terhadap US dollar, data pertama adalah 14.485,07 dan data kedua adalah 14.293,11. Sehingga perhitungan return pada periode pertama dengan memakai persamaan (1) yaitu:
14.293,11
-
rι = lni448S,07=-0,013341
Dengan metode yang serupa, nilai return dihitung pada periode t = 2,3,... ,559 untuk data nilai tukar rupiah terhadap US dollar.
Analisis deskriptif mengenai data return nilai tukar rupiah terhadap US dollar bisa ditemukan melalui Tabel 1.
Tabel 1. Statistika Deskriptif Data Return Nilai Tukar Rupiah Terhadap US Dollar
|
Statistika Deskriptif |
Nilai |
|
Maximum |
0,035083 |
|
Minimum |
-0,02500 |
|
Mean |
0,000022 |
|
Deviasi Standar |
0,004892 |
|
Kurtosis |
11,17140 |
|
Skewness |
0,956387 |
Nilai mean positif melalui Tabel 1 menunjukkan adanya kemungkinan memperoleh keuntungan. Nilai return tersebut mempunyai nilai standar deviasi yang tidak setara atau nilai yang tidak nol, menunjukkan yaitu data tersebut tidak sama atau sesuatu yang mempunyai kecenderungan pada data berbeda (heterogen). Kemudian pada data return mempunyai kurtosis memiliki nilai lebih dari tiga yang menunjukkan yaitu nilai return mempunyai bentuk kurva sebarang yang meruncing yang berarti nilai return tidak berdistribusi normal. Selain nilai kurtosis, sebaran data juga bisa ditinjau dari nilai skewness. Terdeteksi bahwa distribusi data return mempunyai ekor kanan yang lebih panjang dari ekor kiri, artinya data return tersebut memiliki nilai skewness yang lebih besar dari nol. Oleh karena itu, pada data return terdapat ketidaksimetrisan.
Data return nilai tukar rupiah terhadap US dollar menghasilkan plot yang ditampilkan pada Gambar 1.
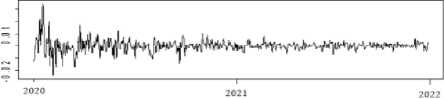
Gambar 1. Plot Data Return Nilai Tukar Rupiah Terhadap US Dollar
Gambar 1, menunjukkan yaitu data return tersebut stasioner dalam mean, yang artinya data return nilai tukar rupiah terhadap US dollar bergerak pada kisaran nilai mean. Ada beberapa teknik atau cara untuk melihat dan mengukur data stasioner, beberapa diantaranya harus terlihat dari grafik korelogram ACF dan PACF. Kedua bisa diuji memakai uji ADF. Berikut ini adalah grafik korelogram nilai ACF dan PACF yang bisa diperlihatkan pada Gambar 2.
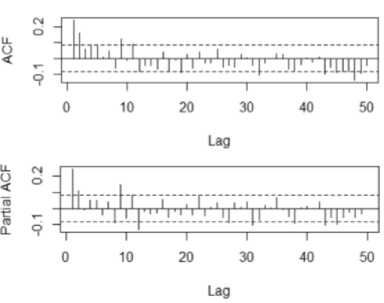
Gambar 2. Grafik ACF dan PACF Data Return
Berdasarkan Gambar 2, hanya beberapa lag keluar dari garis putus-putus (garis bartlett). Namun secara umum, data sudah stasioner.
Berdasarkan data return pada data dan perhitungan memakai persamaan (2), diperoleh hasil uji ADF dengan taraf signifikan 0,05, nilai tukar rupiah terhadap US dollar memiliki nilai p-value sebesar 0,01. Dengan demikian H0 ditolak yang berarti data return sudah stasioner.
Berdasarkan data return akan dihitung nilai Q untuk uji Ljung-Box dan nilai LM memakai untuk menguji ARCH-LM.
Hasil Uji Ljung-Box diperoleh p-value 2,2 × 10-16. Karena p-value lebih rendah dibandingkan taraf signifikan 0,05, terdapat bukti yang cukup untuk menolak speku l a s i H 0 .
Hal ini menunjukkan adanya autokorelasi pada data return.
Selain itu hasil uji ARCH-LM diperoleh p-value 2,2 × 10-16 < 0,05 yang artinya tidak cukup bukti untuk menerima H0. Sehingga ditemukan efek ARCH atau heteroskedastisitas pada data return. Model GARCH diterapkan karena terdapat autokorelasi dan efek ARCH pada data return.
Hasil estimasi parameter untuk model GARCH bisa diamati melalui Tabel 2.
Tabel 2. Estimasi Parameter Model GARCH(m,s)
|
Model |
Parameter |
Estimasi Parameter |
t-statistic |
p-value |
|
«0 |
1,959 × 10-7 |
1,691 |
0,04076 | |
|
«1 |
8,244 × 10-2 |
2,605 |
0,00917 | |
|
(1,1) |
£1 |
9,023 × 10-1 |
25,568 |
2 × 10-16 |
|
«0 |
2,649 × 10-7 |
1,707 |
0,05783 | |
|
GARCH |
«1 |
1,118 × 10-1 |
2,624 |
0,00870 |
|
(1,2) |
£1 |
6,350 × 10-1 |
3,068 |
0,00215 |
|
£2 |
2,345 × 10-1 |
1,181 |
2,6 × 10-16 | |
|
«0 |
2,547 × 10-7 |
1,613 |
0,1068 | |
|
GARCH |
«1 |
1,007 × 10-1 |
2,454 |
0,0141 |
|
(2,1) |
«2 |
1 × 10—8 |
0 |
1 |
|
£1 |
8,825 × 10-1 |
18,791 |
2 × 10-16 | |
|
«0 |
3,360 × 10-7 |
1,916 |
0,05540 | |
|
«1 |
6,073 × 10-2 |
2,428 |
0,01520 | |
|
GARCH |
«2 |
8,787 × 10-2 |
2,917 |
0,00353 |
|
(2,2) |
£1 |
1 × 10—8 |
NA |
NA |
|
£2 |
8,246 × 10-1 |
NA |
NA |
Suatu model disebutkan signifikan ketika mempunyai p-value < 0,05. Mengacu pada Tabel 2, model GARCH(1,1) dan GARCH(1,2) menunjukkan signifikan. Selanjutnya, dilakukan penentuan model GARCH terbaik dengan memilih nilai AIC paling kecil.
Model yang signifikan dan memiliki nilai AIC terkecil dilakukan untuk memilih model GARCH terbaik yang bisa diamati melalui Tabel 3.
Tabel 3. Nilai AIC Model GARCH
|
Model |
AIC |
|
GARCH(1,1) |
-8,423104 |
|
GARCH(1,2) |
-8,415345 |
Mengacu melalui Tabel 3, bisa dilihat bahwa nilai AIC yang paling kecil di antara model GARCH adalah model GARCH(1,1). Oleh karena itu, model yang dipilih adalah model GARCH(1,1). Sehingga model GARCH(1,1) pada nilai tukar rupiah terhadap US dollar dan nilai parameter «0, «1, dan β1 adalah:
σt2 = ao + «1(12-1 + βισ^-ι
= 0,0000001959 +
0,08244d2-1 + 0,9023σt2-1.
Hasil uji sign dan size bias dari model GARCH(1,1) nilai tukar rupiah terhadap US dollar bisa dicermati melalui Tabel 4.
Tabel 4. Uji Sign dan Size Bias Model GARCH(1,1)
|
t-statistic |
p-value |
Sig | |
|
Sign Bias |
0,4445994 |
0,65678325 | |
|
Negative Size Bias |
0,1372183 |
0,89090819 | |
|
Positive Size Bias |
2,1004300 |
0,03614327 |
** |
|
Join Effect |
4,6272990 |
0,20121270 |
Parameter positive size bias adalah signifikan, sebagaimana terlihat dalam Tabel 4. Sehingga, keputusan yang diambil adalah menolak H0 di mana bahwa residu dari model GARCH(1,1) bersifat asimetris. Sehingga volatilitas nilai tukar rupiah terhadap US dollar bisa dimodelkan memakai model GARCH yang bersifat asimetris.
Hasil estimasi parameter model EGARCH, TGARCH, dan APARCH pada nilai tukar rupiah terhadap US dollar disajikan tersendiri dalam Tabel 5, Tabel 6, dan Tabel 7.
Tabel 4. Estimasi Parameter Model EGARCH Return Nilai Tukar Rupiah Terhadap US Dollar
|
Model |
Parameter |
Estimasi Parameter |
t-statistic |
p-value |
|
EGARCH |
«0 |
-0,106486 |
-26,4786 |
0 |
|
(1,1) |
«1 |
0,011414 |
7,0916 |
0 |
|
Λ |
0,989927 |
5075,9260 |
0 | |
|
/1 |
0,139315 |
4,8480 |
0,000001 | |
|
EGARCH |
«0 |
-0,087397 |
-2,72551 |
0,0 0642 0 |
|
(1,2) |
«1 |
0,040502 |
1,15569 |
0,247807 |
|
β1 |
0,531884 |
589,49261 |
0 | |
|
β2 |
0,459781 |
392,26682 |
0 | |
|
/1 |
0,148537 |
1,88618 |
0,059271 | |
|
EGARCH |
«0 |
-0,012418 |
-7,9110× 10 |
0 |
|
(2,1) |
«1 |
0,176381 |
3,8349 × 10 |
0,000126 |
|
«2 |
-0,149147 |
-2,9495× 10 |
0,003183 | |
|
Λ |
0,998975 |
1,6022 × 106 |
0 | |
|
/1 |
0,163577 |
4,5327 × 10 |
0,000006 | |
|
/2 |
-0,123143 |
-2,8614×10 |
0,004217 | |
|
EGARCH |
«0 |
-0,171551 |
-1,53957 |
0,123666 |
|
(2,2) |
«1 |
0,063576 |
2,76591 |
0,005676 |
|
«2 |
-0,038309 |
-2,02302 |
0,043072 | |
|
β1 |
0,016881 |
1,64969 |
0,099007 | |
|
β2 |
0,966997 |
10730,30717 |
0 | |
|
/1 |
0,140190 |
3,62044 |
0,000294 | |
|
/2 |
0,108606 |
2,44421 |
0,014517 |
Tabel 6. Estimasi Parameter Model TGARCH Return Nilai Tukar Rupiah Terhadap US Dollar
|
Model |
Parameter |
Estimasi Parameter |
t-statistic |
p-value |
|
«0 |
6,185 × 10-5 |
1,448 |
0,0476 | |
|
TGARCH |
«1 |
9,495 × 10-2 |
2,550 |
0,0108 |
|
(11) |
β1 |
7,550 × 10-3 |
0,061 |
0,0510 |
|
/1 |
9,128 × 10-1 |
24,771 |
2 × 10-16 | |
|
«0 |
4,146 × 10-5 |
1,163 |
0,2446 | |
|
TGARCH |
«1 |
8,916 × 10-2 |
2,448 |
0,0144 |
|
β1 |
-1,696×10-1 |
-0,755 |
0,4502 | |
|
(1,2) |
β2 |
5,463 × 10-1 |
2,056 |
0,0398 |
|
/1 |
3,752 × 10-1 |
1,358 |
0,1745 | |
|
«0 |
8,482 × 10-5 |
1,363 |
0,1729 | |
|
«1 |
1,158 × 10-1 |
2,269 |
0,0233 | |
|
TGARCH |
«2 |
1 × 10-8 |
0,001 |
0,9993 |
|
(2,1) |
β1 |
1,731 × 10-3 |
0,015 |
0,9879 |
|
/1 |
1,209 × 10-1 |
NA |
NA | |
|
/2 |
8,922 × 10-1 |
17,361 |
2 × 10-16 | |
|
«0 |
5,894 × 10-5 |
1,494 |
0,13515 | |
|
«1 |
7,007 × 10-2 |
2,792 |
0,00524 | |
|
TGARCH |
«2 |
6,122 × 10-2 |
2,196 |
0,02813 |
|
β1 |
-5,84× 10-1 |
-2,706 |
0,00682 | |
|
(2,2) |
β2 |
5,834 × 10-1 |
3,919 |
8,88× 10-5 |
|
/1 |
1 × 10-8 |
NA |
NA | |
|
/2 |
8,847 × 10-1 |
NA |
NA |
Tabel 7. Estimasi Parameter Model APARCH Return Nilai Tukar Rupiah Terhadap US Dollar
|
Model |
Parameter |
Estimasi Parameter |
t-statistic |
p-value |
|
APARCH |
«0 |
0 |
0,017446 |
0,986081 |
|
(1,1) |
«1 |
0,064586 |
2,678108 |
0,00 7404 |
|
β1 |
0,891210 |
18,826832 |
0 | |
|
/1 |
0,022725 |
0,390146 |
0,696428 | |
|
δ |
2,611074 |
33,313757 |
0 | |
|
APARCH |
«0 |
0 |
0,005288 |
0 |
|
(1,2) |
«1 |
0,063618 |
2,553730 |
0,010658 |
|
β1 |
0,453837 |
2,420853 |
0,015484 | |
|
β2 |
0,437168 |
2,563754 |
0,010355 | |
|
/1 |
-0,039207 |
-1,053043 |
0,002321 | |
|
δ |
2,644953 |
36,521069 |
0 | |
|
APARCH |
«0 |
0 |
0,01829 |
0,985407 |
|
(2,1) |
«1 |
0,031797 |
1,96403 |
0,049527 |
|
«2 |
0,027837 |
2,38594 |
0,017035 | |
|
βι |
0,897425 |
27,42135 |
0 | |
|
/1 |
-0,030116 |
-0,15864 |
0,873952 | |
|
/2 |
0,057020 |
0,20160 |
0,840228 | |
|
δ |
2,566999 |
64,17617 |
0 | |
|
APARCH |
«0 |
0 |
0,016198 |
0,987076 |
|
(2,2) |
«1 |
0,030885 |
0,655645 |
0,512052 |
|
«2 |
0,028597 |
2,453249 |
0,014157 | |
|
βι |
0,418044 |
4,512734 |
0,000006 | |
|
β2 |
0,475990 |
17,244133 |
0 | |
|
/1 |
-0,181918 |
-0,309794 |
0,756717 | |
|
/2 |
0,149529 |
0,900709 |
0,367743 | |
|
δ |
2,573845 |
43,277230 |
0 |
Berdasarkan Tabel 5, 6, dan 7 diperoleh bahwa di antara hasil estimasi parameter model EGARCH, TGARCH, dan APARCH nilai tukar rupiah terhadap US dollar, model EGARCH(1,1), EGARCH(2,1), TGARCH(1,1), &APARCH(1,2) yang memiliki tingkat signifikansi karena memperoleh nilai p-value < 0,05. Kemudian, dipilih model terbaik dari model-model tersebut.
Nilai AIC dari model EGARCH, TGARCH, dan APARCH pada nilai tukar rupiah terhadap US dollar bisa diamati melalui Tabel 8.
Tabel 5. Nilai AIC Model EGARCH, TGARCH, APARCH
|
Model |
AIC |
|
EGARCH(1,1) |
-8,3943 |
|
EGARCH(2,1) |
-8,4017 |
|
TGARCH(1,1) |
2,4619 |
|
APARCH(1,2) |
-8,4254 |
Nilai AIC yang diperoleh dari Tabel 8 menunjukkan yaitu AIC yang paling kecil diantara model EGARCH, TGARCH dan APARCH adalah model APARCH(1,2).
Persamaan model APARCH(1,2) untuk data return nilai tukar rupiah terhadap US dollar berdasarkan persamaan (9) adalah
σf = αo + cc1(∖at-1l + γ1at-1)δ + β1σ{-1 + β2σt-2
= 0,063618(∣αt-1∣0,039207αt-1)2'6449≡3
+ 0,453837σt2-644953 0,437168σt2-6244953.
Hasil peramalan volatilitas untuk return nilai tukar rupiah terhadap US dollar selama 14 periode berikutnya, mulai 3 Juni 2022 sampai 16 Juni 2022 yang dihasilkan memakai model APARCH(1,2) ditunjukkan melalui Tabel 9.
Tabel 6. Hasil Peramalan Volatilitas Return Nilai Tukar Rupiah Terhadap US Dollar
|
Tanggal |
Hasil Peramalan |
|
3 Juni 2022 |
0,002602 |
|
4 Juni 2022 |
0,002547 |
|
5 Juni 2022 |
0,002570 |
|
6 Juni 2022 |
0,002558 |
|
7 Juni 2022 |
0,002561 |
|
8 Juni 2022 |
0,002557 |
|
9 Juni 2022 |
0,002557 |
|
10 Juni 2022 |
0,002555 |
|
11 Juni 2022 |
0,002554 |
|
12 Juni 2022 |
0,002553 |
|
13 Juni 2022 |
0,002551 |
|
14 Juni 2022 |
0,002550 |
|
15 Juni 2022 |
0,002549 |
|
16 Juni 2022 |
0,002548 |
Berdasarkan Tabel 9, hasil peramalan pada periode pertama sampai periode empat belas sebesar 0,002602 sampai 0,002548, di mana prakiraan volatilitas return nilai tukar rupiah terhadap US dollar selama 14 periode berikutnya mengalami penurunan dari periode awal hingga periode keempat belas. Hal ini menunjukkan adanya penurunan tingkat return pada periode tersebut. Penurunan volatilitas yang terus menerus menunjukkan bahwa nilai tukar rupiah terhadap US dollar semakin stabil. Peramalan akan menjadi lebih akurat jika dilakukan dalam jangka waktu yang lebih pendek, khususnya untuk 14 periode berikutnya, mengingat data keuangan cenderung berubah setiap waktunya.
Setelah dilakukan analisis terhadap data nilai tukar rupiah terhadap US dollar periode 2 Maret 2020 sampai 2 Juni 2022 diperoleh model terbaik untuk memodelkan volatilitas nilai tukar rupiah terhadap US dollar adalah APARCH(1,2) dengan persamaan modelnya sebagai berikut: σtδ = 0,063618(∣at-1∣0,039207at-1)2'644953 + 0,453837σt2-6144953 + 0,43 7 1 68σt2-6244953
Hasil peramalan volatilitas return nilai tukar rupiah terhadap US dollar dengan memakai model APARCH(1,2) didapat mengalami penurunan sampai periode ke empat belas, yang berarti bahwa tingkat return selama periode tersebut mengalami penurunan. Penurunan volatilitas yang terus menerus menunjukkan nilai tukar rupiah terhadap US dollar semakin stabil. Investor dapat melakukan investasi pada periode waktu tersebut karena penurunan volatilitas dapat
mengindikasikan stabilitas nilai tukar rupiah terhadap US dollar yang dapat mengurangi risiko mata uang.
Mengingat pada penelitian ini hanya memakai model EGARCH, TGARCH, dan APARCH yang di mana penelitian ini belum melibatkan model lain untuk dijadikan perbandingan. Untuk penelitian berikutnya dapat mempertimbangkan untuk menambahkan perbandingan dengan berbagai model lainnya guna menetapkan model terbaik, seperti EGARCH-M, IGARCH, GJR-GARCH atau model asimetris lainnya.
DAFTAR PUSTAKA
Bau, A. F., Kumaat, R. J., & Niode, A. O. 2016. Faktor-faktor yang Mempengaruhi Fluktuasi Nilai Tukar Rupiah Terhadap Dollar Amerika Serikat. Jurnal Berkala Ilmiah Efisiensi, 16(3), 524-535.
Dewi, N. S. 2012. Neural Network Ensembles Untuk Peramalan Nilai Tukar Dollar Terhadap Rupiah. Skripsi: Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sebelas Maret Surakarta.
Elvitra, C. W., Warsito, B., & Hoyyi, A. 2013. Metode Peramalan dengan Memakai Model Volatilitas Asymmetric Power Arch (APARCH). Jurnal Gaussian, 2(4), 289–300.
Firman, N. A. 2020. Model Peramalan Kurs Referensi Dollar Terhadap Rupiah Memakai Metode Jaringan Syaraf Tiruan dengan Propogasi Balik. Skripsi: Program Studi Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Hasanuddin Makassar.
Laila. N. F. 2018. Perbandingan Prakiraan Return Kurs Dollar Australia Terhadap Rupiah Menggunakan Model Exponential GARCH dengan Model Threshold GARCH dalam Periode Bulanan dari Januari 2001 sampai dengan Agustus 2017. Skripsi: Program Studi Matematika Fakultas Sains dan Teknologi Universitas Islam Negeri Syarif Hidayatullah Jakarta.
Untari, N., Mattjik, A.A., & Saefuddin, A. 2009. Analisis Deret Waktu dengan Ragam Galat Heterogen dan Asimetrik. Forum Statistika dan Komputasi, (14): 22-33.
Tsay, R. S. 2005. Analysis of Financial Time Series. Second Edition. Canada: John Wiley & Sons,Inc.
88
Discussion and feedback