PENERAPAN NETWORK PLANNING PADA PROYEK PEMBANGUNAN PERUMAHAN MUTIARA RESIDENCE DI DESA PENGAMBENGAN KABUPATEN JEMBRANA
on
E-Jurnal Manajemen Unud, Vol. 7, No. 12, 2018: 6731 - 6758
ISSN: 2302-8912
DOI: https://doi.org/10.24843/EJMUNUD.2018.v7.i12.p13
PENERAPAN NETWORK PLANNING PADA PROYEK PEMBANGUNAN PERUMAHAN MUTIARA RESIDENCE DI DESA PENGAMBENGAN KABUPATEN JEMBRANA
Rini Wijaya Kusuma Wardhani¹ Kastawan Mandala²
¹,²Fakultas Ekonomi dan Bisnis Universitas Udayana, Bali, Indonesia e-mail : riniwijaya96@gmail.com
ABSTRAK
Peningkatan jumlah perusahaan konstruksi di Indonesia menimbulkan tantangan bagi perusahaan untuk meningkatkan efektifitas dan efisiensi pada pengelolaan sumber daya agar mampu unggul di antara para pesaing. Tujuan penelitian ini adalah untuk mengetahui apakah penerapan Network Planning dapat meningkatkan efisiensi dan efektifitas dalam pengalokasian waktu dan biaya pada proyek konstruksi. Metode penelitian berupa studi kasus dengan menjawab permasalahan pada PT Putra Dewata Karya Tama mengenai perencanaan jaringan kerja proyek pembangunan Perumahan Mutiara Residence. Teknik analisis data yang digunakan adalah Critical Path Method. Hasil penelitian menunjukkan bahwa waktu penyelesaian proyek tersebut adalah 142,5 hari, lebih cepat 14,5 hari dibandingkan dengan hasil perhitungan oleh perusahaan dengan metode Gantt Chart. Hal ini akan memberikan keuntungan dari segi biaya penyelesaian proyek, di mana efisiensi biaya yang dapat diperoleh adalah sebesar Rp. 20.807.500.
Kata Kunci: network planning, critical path method, jalur kritis.
ABSTRACT
The increasing number of construction companies in Indonesia poses a challenge for companies to improve the effectiveness and efficiency of resource management in order to excel among competitors. The purpose of this study is to determine whether the implementation of Network Planning can improve efficiency and effectiveness in the allocation of time and cost on the construction project. The research method is a case study to address the problem at Putra Dewata PT Karya Tama concerning network planning of Mutiara Residence Housing project. Data analysis technique used is Critical Path Method. The results show that the project completion time is 142.5 days, 14.5 days faster than the calculation result by the company with Gantt Chart method. This will provide benefits in terms of cost of completion of the project, where cost efficiencies that can be gained is Rp. 20,807,500.
Keywords: network planning, critical path method, critical path.
PENDAHULUAN
Provinsi Bali merupakan salah satu provinsi di Indonesia dengan tingkat kepadatan penduduk yang cukup tinggi. Menurut Laporan Badan Pusat Statistik Tahun 2017, jumlah penduduk di Provinsi Bali tahun 2017 telah mencapai 4,2 juta jiwa dengan peningkatan sebesar 1,09 persen dari tahun 2016. Kepadatan penduduk di Provinsi Bali telah mencapai 745 jiwa per kilometer kuadrat dengan luas wilayahnya sebesar 5.636,66 km2 (BPS Provinsi Bali, 2017). Peningkatan jumlah penduduk di suatu daerah akan mempengaruhi besarnya kebutuhan primer di daerah tersebut, salah satunya kebutuhan akan tempat tinggal yang menjadi semakin tinggi.
Tingginya permintaan akan tempat tinggal menimbulkan dibutuhkan lebih banyak lagi pembangunan rumah tinggal agar kebutuhan masyarakat dapat terpenuhi. Berdasarkan hal tersebut, tidak sedikit para pengembang yang memanfaatkan peluang bisnis tersebut untuk berinvestasi di bidang property. Besarnya permintaan terhadap tempat tinggal memunculkan persaingan ketat antar-pengembang bisnis property untuk membangun suatu kawasan pemukiman baru yang memberikan kenyamanan, keamanan serta harga yang terjangkau. Seiring dengan meningkatnya permintaan pembangunan perumahan atau hunian, menjadikan keberadaan perusahaan jasa konstruksi di Indonesia semakin meningkat.
Peningkatan jumlah perusahaan konstruksi di Indonesia pada akhirnya akan meningkatkan persaingan dan menimbulkan tantangan tersendiri bagi perusahaan untuk dapat meningkatkan kinerja perusahaan di antara para pesaing. Salah satu
upaya yang dapat dilakukan adalah meningkatkan efektifitas dan efisiensi dengan memaksimalkan pengelolaan sumber daya yang dimiliki baik pengelolaan waktu, biaya, maupun kualitas untuk mencapai keberhasilan dalam pelaksanaan proyek.
Menurut Handoko (2016:125) masalah signifikan dalam manajemen proyek terdapat pada perencanaan, pengurutan, scheduling dan pengawasan kegiatan-kegiatan yang mempengaruhi penyelesaian proyek secara keseluruhan. Dalam pelaksanaan sebuah proyek, kerap terjadi keterlambatan pada pelaksanaan, dan pembiayaan yang melampaui batas anggaran (Widiasanti dan Lenggogeni, 2013:48). Oleh karena itu, tim proyek harus dapat menyiapkan perencanaan secara terperinci sehingga seluruh kegiatan proyek dapat dijadwalkan, dianggarkan, dimonitor, dan dikendalikan dengan baik.
PT Putra Dewata Karya Tama merupakan perusahaan yang bergerak di bidang konstruksi yang beroperasi di Provinsi Bali sejak tahun 1997. Perusahaan memiliki lingkup pelayanan jasa konstruksi seperti mendirikan bangunan tempat tinggal, pertokoan, perkantoran, hotel dan sebagainya. Menurut Direktur PT Putra Dewata Karya Tama, dalam pelaksanaan pembangunan proyek, perusahaan kerap mengalami keterlambatan penyelesaian proyek yang diakibatkan oleh cuaca buruk serta kinerja tenaga kerja langsung yang masih dianggap kurang terampil. Selama ini, dalam membuat penjadwalan proyek, perusahaan melakukan perhitungan dan penyusunan jadwal secara sederhana dengan menggunakan Gantt Chart. Gantt Chart merupakan metode yang menggambarkan aktivitas pengerjaan ke dalam bentuk bagan balok, dengan panjang balok sebagai representasi dari durasi setiap kegiatan (Husen, 2010:152).
PT Putra Dewata Karya Tama menggunakan Gantt Chart sebagai metode penjadwalan proyek karena dianggap sederhana dan mudah dibaca, namun metode ini diidentifikasi masih memiliki kekurangan. Menurut Husen (2010:152) penyajian informasi pada metode Gantt Chart agak terbatas, yakni tidak menunjukkan secara spesifik hubungan ketergantungan antar-kegiatan, lintasan kritis kegiatan proyek tidak dapat diketahui dan urutan kegiatan kurang terinci sehingga bila terjadi keterlambatan proyek, prioritas kegiatan yang akan dikoreksi menjadi sukar untuk dilakukan. Pernyataan tersebut juga didukung dari penelitian oleh Geraldi dan Lechter (2017) yang menemukan bahwa Gantt Chart tidak dapat secara eksplisit mengatasi kompleksitas, ambiguitas, ketidakpastian serta perubahan dalam pelaksanaan proyek. Akibatnya pada perusahaan, ketika terjadi keterlambatan penyelesaian proyek selain akibat cuaca yang buruk, perusahaan kerap kali kesulitan untuk mengetahui secara pasti kegiatan mana yang menyebabkan keterlambatan penyelesaian proyek.
Network Planning merupakan salah satu metode yang dapat digunakan untuk membantu me-manage dalam perencanaan dan pengendalian proyek (Dharma, 2013). Hasil penelitian oleh Adebowale dan Oluboyede (2011) menyatakan bahwa manajemen dalam pembangunan proyek dapat ditingkatkan jika teknik analisis jaringan diadopsi. Salah satu metode dasar yang dapat digunakan dalam penerapan network planning yaitu Critical Path Method (CPM). Critical Path Method merupakan dasar dari sistem perencanaan dan pengendalian suatu pekerjaan berdasarkan pada network atau jaringan kerja (Pratasik, 2013). Penelitian terdahulu oleh Wahyuni (2011) menghasilkan efisiensi waktu terhadap
proyek smart graduate sebesar 42 hari dari waktu seharusnya dengan menggunakan metode jalur kritis. Penelitian yang sama juga dilakukan oleh Adedeji & Bello (2011), Elias & Ismail (2012), Sahid (2012), Syafridon dan Syahrizal (2013), Sugiarto dkk. (2013), Dharma (2013), Nugraha dan Marjono (2014), Anggriawan (2015), Permana dan Kholil (2016), Nalhadi dan Suntana (2017), serta Purhariani (2017).
Berdasarkan latar belakang yang telah diuraikan sebelumnya, maka rumusan masalah yang dibuat dalam penelitian ini adalah: 1) Bagaimana perencanaan jaringan kerja (network planning) pada proyek pembangunan Perumahan Mutiara Residence?, 2) Bagaimanakah jalur kritis pada proyek pembangunan Perumahan Mutiara Residence?, 3) Berapa waktu yang dibutuhkan untuk menyelesaikan proyek pembangunan Perumahan Mutiara Residence dengan metode jalur kritis (Critical Path Method)?, 4) Berapa biaya total proyek pembangunan Perumahan Mutiara Residence dengan penggunaan metode jalur kritis (Critical Path Method)?
Penelitian ini bertujuan untuk 1) Menentukan perencanaan jaringan kerja (network planning) pada proyek pembangunan Perumahan Mutiara Residence, 2) Menentukan jalur kritis pada proyek pembangunan Perumahan Mutiara Residence, 3) Menentukan waktu yang dibutuhkan untuk menyelesaikan proyek pembangunan Perumahan Mutiara Residence dengan metode jalur kritis (Critical Path Method), 4) Mengetahui biaya total proyek pembangunan Perumahan Mutiara Residence pada penggunaan metode jalur kritis (Critical Path Method).
Menurut Schwalbe yang diterjemahkan oleh Dimyati dan Nurjaman (2014:2) proyek adalah usaha yang bersifat sementara untuk menghasilkan produk atau layanan yang unik. Di sisi lain, Rani (2016:14) menjelaskan bahwa proyek adalah suatu kegiatan yang dilakukan dengan waktu dan sumber daya terbatas untuk mencapai hasil akhir yang ditentukan. Dalam mencapai hasil akhir, kegiatan proyek dibatasi oleh anggaran, jadwal, dan mutu, yang dikenal sebagai tiga kendala (triple constraint).
Manajemen proyek merupakan suatu upaya dalam perencanaan, pengorganisasian, pengarahan dan pengendalian sumber daya pada suatu organisasi atau perusahaan untuk mencapai tujuan tertentu dalam waktu tertentu dengan sumber daya tertentu (Santosa, 2009:3). Tujuan utama manajemen proyek adalah agar semua rangkaian kegiatan tersebut tepat waktu, tepat biaya, dan kualitas serta proses sesuai dengan persyaratan. Untuk mencapai tujuan tersebut, perlu dilakukan pengawasan terhadap mutu, biaya, dan waktu. Oleh karena itu, dilakukan pelaksanaan pengawasan mutu (quality control), pengawasan biaya (cost control), dan pengawasan waktu pelaksanaan (time control). Ketiga pengawasan ini dilakukan secara bersamaan (Dimyati dan Nurjaman, 2014:26).
Jaringan kerja merupakan cara grafis untuk menggambarkan kegiatan-kegiatan dan kejadian yang diperlukan untuk mencapai harapan-harapan proyek (Risnawati, 2014). Menurut Rani (2016:39) kegunaan network planning dalam manajemen proyek adalah dalam network planning ditunjukkan dengan jelas pekerjaan-pekerjaan yang waktunya penyelesaiannya kritis dan yang tidak, sehingga memungkinkan pengaturan pembagian usaha terhadap pekerjaan
tersebut. Critical Path Method (CPM) merupakan dasar dari sistem perencanaan dan pengendalian kemajuan pekerjaan yang didasarkan pada network atau jaringan kerja. CPM pertama kali digunakan di Inggris pada pertengahan tahun 50-an untuk membantu manajer proyek dalam melakukan penjadwalan, pengawasan, serta pengendalian proyek (Heizer dan Render, 2009:93).
Pada sebuah jaringan terdapat waktu slack dan jalur kritis. Jalur kritis adalah lintasan dari kegiatan-kegiatan yang waktu pelaksanaan dari kegiatan tersebut tidak boleh ditunda (Rani, 2016:42). Terdapat dua cara untuk melakukan analisis waktu optimal, yaitu menggunakan perhitungan maju (forward pass) dari kegiatan awal sampai kegiatan akhir dan menggunakan perhitungan mundur (backward pass) mulai kegiatan akhir kembali ke kegiatan awal.
Pada jalur kritis, kegiatan yang tidak memiliki waktu tenggang (S = 0), berarti kegiatan tersebut harus dimulai tepat pada ES sehingga tidak mengakibatkan bertambahnya waktu penyelesaian proyek. Kegiatan yang nilai slack = 0 disebut sebagai kegiatan kritis serta berada pada jalur kritis. Sebuah jalur kritis terdiri dari pekerjaan-pekerjaan yang tidak bisa ditunda waktu pengerjaannya. Selanjutnya analisis jalur kritis akan digunakan dalam membantu menentukan jadwal proyek.
Berdasarkan latar belakang, rumusan masalah, tujuan, dan kajian pustaka khususnya pada komponen dasar Network Planning yang telah dijelaskan sebelumnya, maka dapat diketahui model kerangka konseptual penelitian yang digambarkan sebagai berikut.
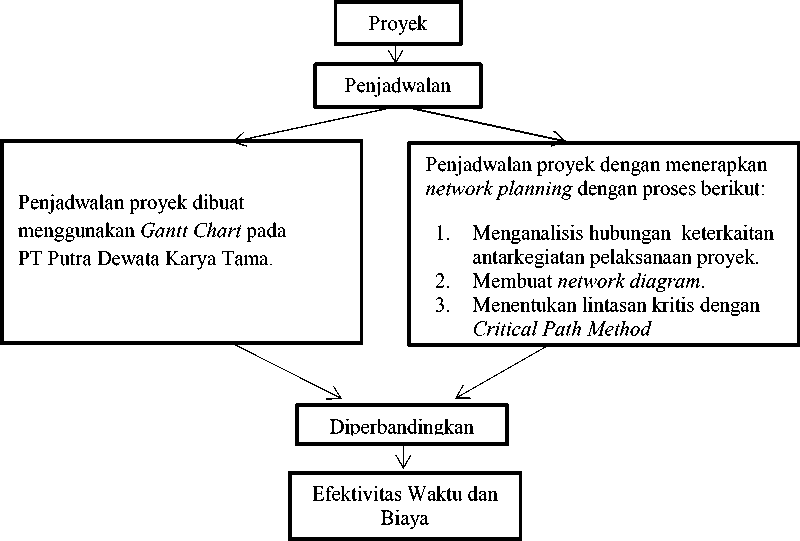
Gambar 1. Kerangka Konseptual
METODE PENELITIAN
Penelitian ini termasuk ke dalam penelitian deskriptif dengan menggunakan pendekatan kuantitatif. Metode yang digunakan dalam penelitian ini adalah studi kasus yang mana bertujuan untuk menjawab permasalahan perusahaan mengenai perencanaan jaringan kerja pada PT Putra Dewata Karya Tama. Penelitian ini dilakukan pada PT Putra Dewata Karya Tama yang berlokasi di Jl. Kebo Iwa No.15 X, Denpasar Barat dan lokasi proyek perumahan Mutiara Residence di Desa Pengambengan, Kabupaten Jembrana. Obyek dalam penelitian ini adalah network planning pada proyek pembangunan Perumahan Mutiara Residence milik PT Dewata Property Group dengan kontraktor pelaksana PT Putra Dewata Karya Tama.
Variabel-variabel yang dianalisis sesuai dengan masalah utama dan tujuan yang ingin dicapai dalam penelitian ini adalah Jenis Pekerjaan (kegiatan), Waktu Pekerjaan (waktu normal), Biaya Pekerjaan (biaya normal), Aktivitas Pendahulu (predecessor), Jalur Kritis, dan Biaya Total. Data kuantitatif yang digunakan dalam penelitian ini meliputi data waktu pekerjaan (durasi kegiatan), jadwal pelaksanaan proyek berupa diagram Gantt, Rencana Anggaran Pelaksanaan (RAP) proyek, dan jumlah kebutuhan tenaga kerja. Sedangkan untuk data kualitatif yang digunakan dalam penelitian ini meliputi gambaran umum perusahaan, gambaran umum proyek, data jenis pekerjaan (kegiatan dalam proyek), dan hubungan ketergantungan antar-kegiatan (data kegiatan terdahulu). Berdasarkan data durasi masing-masing kegiatan dan hubungan ketergantungan antarkegiatan yang didapatkan dari perusahaan, maka akan dilakukan perencanaan jaringan kerja dan penjadwalan penyelesaian proyek. Teknik penjadwalan dalam penelitian ini menggunakan Critical Path Method.
Critical Path Method
Critical Path Method merupakan analisa jaringan kerja yang berusaha mengoptimalkan biaya total proyek melalui pengurangan atau percepatan waktu penyelesaian total proyek yang bersangkutan. Langkah-langkah untuk menganalisis data pada penelitian ini adalah sebagai berikut: 1) Menginventarisasi kegiatan berdasarkan item pekerjaan, lalu diberi kode kegiatan untuk memudahkan identifikasi; 2) Membangun hubungan antara aktivitas-aktivitasnya. Memutuskan kegiatan yang harus dilakukan lebih dahulu dan kegiatan yang harus mengikuti kegiatan lain; 3) Menentukan waktu atau durasi pada tiap-tiap kegiatan
berdasarkan data durasi kegiatan yang diperoleh dari para responden; 4) Menggambarkan diagram jaringan kerja atau network diagram yang menghubungkan keseluruhan kegiatan dengan melakukan perhitungan maju (forward pass) dari kegiatan awal sampai kegiatan akhir dan menentukan nilai earliest start (ES) dan earliest finish (EF) pada tiap-tiap kegiatan dengan rumus:
ES = Max {EF seluruh pendahulu langsung}……………………………….(1)
EF = ES kegiatan tersebut + Waktu kegiatan tersebut…………………..…..(2)
selanjutnya melakukan perhitungan mundur (backward pass) mulai kegiatan akhir kembali ke kegiatan awal dengan menentukan nilai latest start (LS) dan latest finish (LF) pada tiap-tiap kegiatan dengan rumus:
LS = LF kegiatan tersebut – Waktu kegiatan tersebut……………………....(3)
LF = Min {LS dari seluruh aktivitas yang langsung mengikutinya}…….….(4)
5) Menentukan jalur waktu terpanjang atau lintasan kritis dengan Critical Path Method dengan menghitung waktu tenggang (slack) pada tiap-tiap kegiatan dengan formula sebagai berikut:
Slack = LS – ES …………………………………………………...……….(5)
Slack = LF – EF ....……………………………………………...………….(6)
dan 6) Menghitung biaya total pelaksanaan proyek dengan menjumlahkan biaya langsung (direct cost) dan biaya tidak langsung (indirect cost).
HASIL DAN PEMBAHASAN
Berdasarkan data durasi masing-masing kegiatan yang telah diperoleh, dilakukan penyusunan diagram jaringan kerja atau network diagram yang menghubungkan keseluruhan kegiatan dengan jaringan kerja AON untuk
mengetahui waktu penyelesaian proyek. Berikut data mengenai kegiatan terdahulu dan durasi masing-masing kegiatan pelaksanaan proyek.
Tabel 1.
Durasi Kegiatan Pada Pelaksanaan Proyek Pembangunan Perumahan Mutiara Residence
|
No |
Jenis Pekerjaan (Kegiatan) |
Kode Kegiatan |
Kegiatan Pendahulu |
Durasi Kegiatan (hari) |
|
1 |
Survei lokasi |
A1 |
- |
1 |
|
2 |
Perhitungan anggaran biaya pembangunan |
A2 |
A1 |
3 |
|
3 |
Pelaksanaan tender |
A3 |
A2 |
20 |
|
4 |
Penandatanganan surat kontrak |
A4 |
A3 |
1 |
|
5 |
Pembentukan tim pelaksana |
A5 |
A4 |
7 |
|
6 |
Perencanaan dan penjadwalan proyek |
A6 |
A5 |
3 |
|
7 |
Pembuatan KIPEM |
A7 |
A5 |
2 |
|
8 |
Pembersihan area |
B1 |
A6, A7 |
1 |
|
9 |
Penataan jalan lingkungan |
B2 |
A6, A7 |
1 |
|
10 |
Pemasangan listrik |
C1 |
B1, B2 |
0.5 |
|
11 |
Pembuatan sumur bor dan pemasangan pompa air |
C2 |
B1, B2 |
0.5 |
|
12 |
Pembuatan kantor (direksi keet) |
D1 |
C1, C2 |
2 |
|
13 |
Pembangunan gudang dan tempat tidur |
D2 |
C1, C2 |
1.4 |
|
14 |
Pembuatan septictank |
D3 |
C1, C2 |
0.5 |
|
15 |
Pembuatan toilet |
D4 |
C1, C2 |
1 |
|
16 |
Pembuatan saluran limbah |
D5 |
C1, C2 |
0.5 |
|
17 |
Pemasangan bouwplank |
E |
D1, D2, D3, D4, D5 |
2.5 |
|
18 |
Galian pondasi |
F |
E |
3.4 |
|
19 |
Pemasangan pondasi batu kali |
G |
F |
3.1 |
|
20 |
Pengecoran sloof |
H |
G |
6.8 |
|
21 |
Pemasangan dinding bata |
I |
H |
14.5 |
|
22 |
Pemasangan kolom praktis |
J |
H |
14.5 |
|
23 |
Pemasangan kusen |
K |
H |
3.3 |
|
24 |
Pengecoran ring balok praktis |
L |
I, J, K |
6.5 |
|
25 |
Pemasangan gewel dan kerangka atap |
M |
L |
14.2 |
|
26 |
Instalasi air dan listrik |
N |
L |
2.8 |
|
27 |
Pemasangan genteng |
O |
M |
6.9 |
|
28 |
Pemlesteran dan acian dinding |
P |
N, O |
20.9 |
|
29 |
Pemasangan plafon |
Q |
P |
8.9 |
|
30 |
Pemasangan keramik lantai rumah |
R |
P |
6.5 |
|
31 |
Pengecatan bangunan |
S |
Q, R |
6.9 |
|
32 |
Pemasangan daun jendela dan daun pintu |
T |
S |
4.7 |
|
33 |
Pengerjaan kamar mandi |
U |
P |
4.9 |
|
34 |
Pekerjaan finishing |
V |
T, U |
2.9 |
|
35 |
Pembersihan bangunan |
W |
V |
1.6 |
Sumber: Data Diolah, 2018
Penentuan waktu penyelesaian suatu proyek pada diagram jaringan dapat dihitung melalui dua cara yaitu menggunakan perhitungan maju (forward pass)
dari kegiatan awal sampai kegiatan akhir dan menggunakan perhitungan mundur (backward pass) mulai kegiatan akhir kembali ke kegiatan awal.
Perhitungan Maju (Forward Pass)
Melakukan perhitungan maju (forward pass) dari kegiatan awal sampai kegiatan akhir dengan menentukan nilai earliest start (ES) dan earliest finish (EF) pada tiap-tiap kegiatan. Forward pass dilakukan dari awal jaringan menuju akhir jaringan. Nilai EF merupakan waktu paling awal suatu aktivitas dapat mulai. Waktu paling cepat dimulainya aktivitas pada kegiatan A1 dianggap 0 karena kegiatan tersebuttidak memiliki kegiatan predecessor. Aturan pada forward pass adalah kecuali kegiatan pertama, kegiatan baru dapat dimulai bila kegiatan sebelumnya (predecessor) telah selesai dilakukan. Waktu mulai paling awal kegiatan berikutnya pada percabangan jaringan diambil dari waktu awal terbesar dari kegiatan sebelumnya (Heizer dan Render, 2009:102).
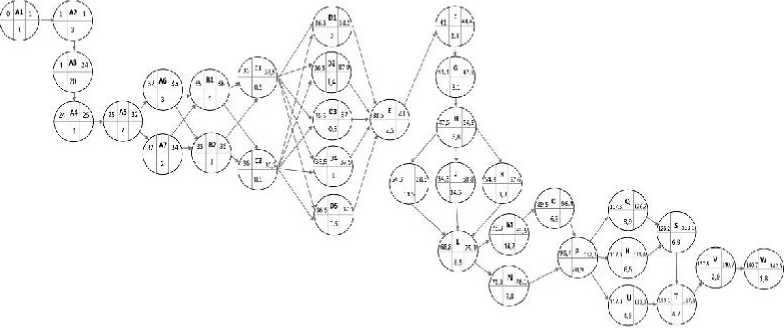
Gambar 2. Diagram Jaringan Kerja Perhitungan Maju Proyek
Pembangunan Perumahan Mutiaraq Residence
Sumber: Data Diolah, 2018
Perhitungan waktu tercepat dimulainya aktivitas (ES) dilakukan dengan menjumlahkan waktu kegiatan awal kegiatan terdahulu (ES) dengan waktu kegiatan terdahulu (t). Perhitungan waktu tercepat selesainya aktivitas (EF) dilakukan dengan menjumlahkan waktu kegiatan awal kegiatan tersebut (ES) dengan waktu kegiatan tersebut (t). Menggunakan rumus (1) maka ES(A1) = 0, karena ES(A1) tidak memiliki kegiatan awal. Menggunakan rumus (2), EF(A1) adalah 1 (= 0 + 1). Hasil perhitungan EF suatu kegiatan merupakan estimasi waktu mulai terbaru dari kegiatan selanjutnya, maka ES(A2) = EF(A1) = 1. Selanjutnya EF(A2) adalah 4 (= 1 + 3), karena kegiatan A2 mendahului kegiatan A3, ES(A3) sama dengan EF(A2) yaitu 4, jadi EF(A3) adalah 24 (= 4 + 20). Setelah kegiatan A3 adalah kegiatan A4 dimana ES(A4) = EF(A3) = 24, dan EF(A4) adalah 25 (= 24 + 1). Setelah kegiatan A4 adalah kegiatan A5 dimana ES(A5) = EF(A4) = 25, dan EF(A5) adalah 32 (= 25 + 7). Kegiatan A6 dan A7 memiliki kegiatan pendahulu yang sama yaitu kegiatan A5, jadi ES(A6) dan ES(A7) = EF(A5) = 32, EF(A6) adalah 35 (= 32 + 3) dan EF(A7) adalah 34 (= 32 + 2).
Tiba pada kegiatan B1 dan B2, baik kegiatan A6 dan A7 adalah pendahulu langsung kegiatan B1 dan B2. Kegiatan A6 memiliki EF = 35 dan kegiatan A7 memiliki EF = 34. Dengan menggunakan aturan waktu selesai paling awal, kita menghitung ES kegiatan B1 sebagai berikut, ES(B1) = max{EF(A6), EF(A7)} = max{35, 34} = 35 dan EF(B1) adalah 36 (= 35 + 1), serta ES kegiatan B2 sebagai berikut, ES(B2) = max{EF(A6), EF(A7)} = max{35, 34} = 35 dan EF(B2) adalah 36 (= 35 + 1). Selanjutnya, kegiatan B1 dan B2 merupakan kegiatan pendahulu
dari kegiatan C1 dan C2. Jadi ES(C1) dan ES(C2) = EF(B1) = EF(B2) = 36, EF(C1) adalah 36,5 (= 36 + 0,5) dan EF(C2) adalah 36,5 (= 36 + 0,5). Selanjutnya, kegiatan C1 dan C2 merupakan kegiatan pendahulu dari 5 kegiatan sekaligus yakni kegiatan D1, D2, D3, D4, D5. Jadi ES(D1) = ES(D2) = ES(D3) = ES(D4) = ES(D5) = max{EF(C1), EF(C2)} = max{36,5 ; 36,5} = 36,5. EF(D1) adalah 38,5 (= 36,5 + 2), EF(D2) adalah 37,9 (= 36,5 + 1,4), EF(D3) adalah 37 (= 36,5 + 0,5), EF(D4) adalah 37,5 (= 36,5 + 1), dan EF(D5) adalah 37 (= 36,5 + 0,5).
Pada kegiatan selanjutnya, kegiatan E memiliki 5 kegiatan pendahulu yaitu kegiatan D1, D2, D3, D4, D5. Jadi ES(E) = max{EF(D1), EF(D2), EF(D3), EF(D4), EF(D5)} = max{38,5 ; 37,9 ; 37 ; 37,5 ; 37} = 38,5, dan EF(E) adalah 41 (= 38,5 + 2,5). Selanjutnya, setelah kegiatan E adalah kegiatan F dimana ES(F) = EF(E) = 41, dan EF(F) adalah 44,4 (= 41 + 3,4). Setelah kegiatan F adalah kegiatan G dimana ES(G) = EF(F) = 44,4, dan EF(G) adalah 47,5 (= 44,4 + 3,1). Setelah kegiatan G adalah kegiatan H dimana ES(H) = EF(G) = 47,5 dan EF(H) adalah 54,3 (= 47,5 + 6,8). Kegiatan H merupakan kegiatan pendahulu dari maing-masing kegiatan I, J, dan K, sehingga ES(I) = ES(J) = ES(K) = EF(H) = 54,3. EF(I) adalah 68,8 (= 54,3 + 14,5), EF(J) adalah 68,8 (= 54,3 + 14,5), dan EF(K) adalah 57,6 (= 54,3 + 3,3).
Tiba pada kegiatan L di mana kegiatan tersebut memiliki 3 kegiatan pendahulu sekaligus yakni kegiatan I, J, dan K, sehingga ES(L) = max{EF(I), EF(J), EF(K)} = max{68,8 ; 68,8 ; 57,6} = 68,8 dan EF(L) adalah 75,3 (= 68,8 + 6,5). Setelah kegiatan L terdapat kegiatan M dan kegiatan N, sehingga ES(M) =
ES(N) = EF(L) = 75,3 serta EF(M) adalah 89,5 (= 75,3 + 14,2) dan EF(N) adalah 78,1 (= 75,3 + 2,8). Selanjutnya, setelah kegiatan M adalah kegiatan O dimana ES(O) = EF(M) = 89,5, dan EF(O) adalah 96,4 (= 89,5 + 6,9). Kegiatan N dan O merupakan kegiatan pendahulu dari kegiatan P, sehingga ES(P) = max{EF(N), EF(O)} = max{78,1 ; 96,4} = 96,4 dan EF(P) adalah 117,3 (= 96,4 + 20,9).
Selanjutnya kegiatan P menjadi kegiatan pendahulu bagi kegiatan Q, R, dan U, sehingga sehingga ES(Q) = ES(R) = ES(U) = EF(P) = 117,3 serta EF(Q) adalah 126,2 (= 117,3 + 8,9), EF(R) adalah 123,8 (= 117,3 + 6,5) dan EF(U) adalah 122,2 (= 117,3 + 4,9). Kegiatan Q dan R selanjutnya menjadi kegiatan pendahulu bagi kegiatan S, sehingga ES(S) = max{EF(Q), EF(R)} = max{126,2 ; 123,8} = 126,2 dan EF(S) adalah 133,1 (= 126,2 + 6,9). Selanjutnya, setelah kegiatan S adalah kegiatan T dimana ES(T) = EF(S) = 133,1, dan EF(T) adalah 137,8 (= 133,1 + 4,7). Kegiatan T dan U selanjutnya menjadi kegiatan pendahulu bagi kegiatan V, sehingga ES(V) = max{EF(T), EF(U)} = max{137,8 ; 122,2} = 137,8 dan EF(V) adalah 140,7 (= 137,8 + 2,9). Selanjutnya, setelah kegiatan V adalah kegiatan terakhir yaitu kegiatan W dimana ES(W) = EF(V) = 140,7, dan EF(W) adalah 142,5 (= 140,7 + 1,8).
Perhitungan Mundur (Backward Pass)
Meskipun forward pass memungkinkan kita menentukan waktu penyeleaian proyek paling awal, teknik ini tidak mengidentifikasi jalur kritisnya. Untuk mengidentifikasi jalur kritis, maka perlu melakukan backward pass untuk menentukan nilai LS dan LF untuk semua aktivitas (Heizer dan Render, 2009:104). Melakukan perhitungan mundur (backward pass) mulai kegiatan akhir
kembali ke kegiatan awal dengan menentukan nilai latest start (LS) dan latest finish (LF) pada tiap-tiap kegiatan.
Gambar 3.
Diagram Jaringan Kerja Perhitungan Mundur Proyek Pembangunan Perumahan Mutiara Residence
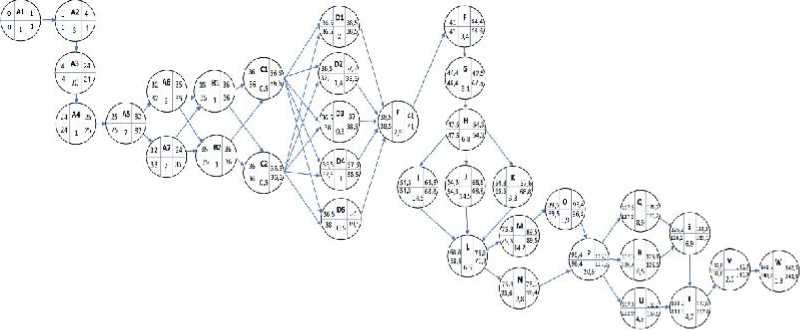
Sumber: Data Diolah, 2018
Backward pass dilakukan dari jaringan terakhir bergerak menuju awal jaringan. Aturan dalam backward pass ialah nilai waktu mulai paling akhir suatu kegiatan sama dengan nilai waktu selesai paling akhir dikurangi durasi berlangsungnya kegiatan tersebut. Waktu selesai paling awal kegiatan selanjutnya pada percabangan jaringan diambil dari waktu selesai terkecil dari kegiatan sebelumnya (Heizer dan Render, 2009:108).
Perhitungan mundur dimulai dengan menentukan nilai LF pada kegiatan terakhir atau kegiatan W sebesar 142,5. Artinya waktu selesai paling lambat untuk keseluruhan proyek sama dengan waktu selesai paling awal. Rumus (3) digunakan untuk menentukan nilai LS suatu kegiatan, maka LS(W) = LF(W) – t = 142,5 – 1,8 = 140,7. Menggunakan rumus (4), nilai LF(V) sama dengan nilai LS(W) karena kegiatan W merupakan satu-satunya kegiatan penerus bagi kegiatan V, jadi LF(V) = LS(W) = 140,7.
Selanjutnya dengan perhitungan serupa, nilai LS(V) adalah 137,8 (= 140,7 – 2,9). Kegiatan V merupakan kegiatan penerus bagi kegiatan T dan U, sehingga LF(T) = LF(U) = LS(V) = 137,8 dan nilai LS(T) dan LS(U) masing-masing adalah 133,1 (= 137,8 – 4,7) dan 132,9 (= 137,8 – 4,9). Selanjutnya, kegiatan T merupakan kegiatan penerus bagi kegiatan S, sehingga LF(S) = LS(T) = 133,1 dan nilai LS(S) adalah 126,2 (= 133,1 – 6,9). Kegiatan S memiliki 2 kegiatan pendahulu yaitu kegiatan Q dan R, sehingga LF(Q) = LF(R) = LS(S) = 126,2 dan nilai LS(Q) dan LS(R) masing-masing adalah 117,3 (= 126,2 – 8,9) dan 119,7 (= 126,2 – 6,5).
Tiba pada kegiatan P dengan 3 kegiatan penerus yakni kegiatan Q, R, dan U. dengan rumus (4), nilai LF(P) = min{LS(Q), LS(R), LS(U)} = min{117,3 ; 119,7 ; 132,9) = 117,3. Nilai LS pada kegiatan P adalah 96,4 (= 117,3 – 20,9). Kegiatan P merupakan kegiatan penerus bagi kegiatan O dan N, sehingga LF(O) = LF(N) = LS(P) = 96,4. Nilai LS pada kegiatan O dan N masing-masing adalah 89,5 (= 96,4 – 6,9) dan 93,6 (= 96,4 – 2,8). Selanjutnya kegiatan O merupakan kegiatan penerus bagi kegiatan M, sehingga LF(M) = LS(O) = 89,5 dan nilai LS(O) adalah 75,3 (= 89,5 – 14,2). Kegiatan M dan N merupakan kegiatan penerus dari kegiatan L, sehingga nilai LF(L) = min{LS(M), LS(N)} = min{75,3 ; 93,6} = 75,3 dan LS(L) adalah 68,8 (= 75,3 – 6,5). Selanjutnya, kegiatan L memiliki 3 kegiatan yang mengikutinya yakni kegiatan I, J, dan K, sehingga nilai LF(I) = LF(J) = LF(K) = LS(L) = 68,8 dan nilai LS pada kegiatan I, J, dan K masing-masing adalah 54,3 (= 68,8 – 14,5), 54,3 (= 68,8 – 14,5), dan 65,5 (= 68,8 – 3,3). Selanjutnya ketiga kegiatan ini merupakan kegiatan penerus bagi kegiatan H,
sehingga nilai LF(H) = min{LS(I), LS(J), LS(K)} = min{54,3 ; 54,3 ; 65,5) = 54,3 dengan nilai LS(H) adalah 47,5 (= 54,3 – 6,8).
Pada kegiatan H, hanya terdapat satu kegiatan pendahulu yaitu kegiatan G, maka nilai LF(G) = LS(H) = 47,5 dan nilai LS(G) adalah 44,4 (= 47,5 – 3,1). Begitu pula dengan kegiatan G yang hanya memiliki satu kegiatan pendahulu yaitu kegiatan F, maka nilai LF(F) = LS(G) = 44,4 dengan nilai LS(F) adalah 41 (= 44,4 – 3,4). Kegiatan F juga merupakan kegiatan penerus dari satu kegiatan yakni kegiatan E, sehingga nilai LF(E) = LS(F) = 41 dengan nilai LS(E) adalah 38,5 (= 41 – 2,5). Tiba pada 5 kegiatan yang merupakan kegiatan pendahulu bagi kegiatan E yakni kegiatan D1, D2, D3, D4, dan D5, sehingga LF(D1) = LF(D2) = LF(D3) = LF(D4) = LF(D5) = LS(E) = 38,5. Nilai LS pada masing-masing kegiatan tersebut adalah 36,5 (= 38,5 –2) ; 37,1 (= 38,5 – 1,4); 38 (= 38,5 – 0,5) ; 37,5 (=38,5–1) ; 38 (= 38,5 – 0,5).
Selanjutnya kegiatan D1, D2, D3, D4, dan D5 masing-masing merupakan kegiatan penerus bagis kedua kegiatan C1 dan C2, sehingga nilai LF(C1) = LF(C2) = min{LS(D1), LS(D2), LS(D3), LS(D4), LS(D5)} = min{36,5 ; 37,1 ; 38 ; 37,5 ; 38) = 36,5. Nilai LS pada kegiatan C1 dan C2 masing-masing adalah 36 (= 36,5 – 0,5) dan 36 (= 36,5 – 0,5). Kegiatan C1 dan C2 selanjutnya merupakan kegiatan penerus dari kegiatan B1 dan B2, sehingga LF(B1) = min{LS(C1), LS(C2)} = min{36 ; 36} = 36 dan LS(B1) adalah 35 (= 36 – 1), dan LF(B2) = min{LS(C1), LS(C2)} = min{36 ; 36} = 36 dan LS(B2) adalah 35 (= 36– 1).
Selanjutnya, kegiatan B1 dan B2 memiliki 2 kegiatan yang mengikutinya yakni kegiatan A6 dan A7, sehingga nilai LF(A6) = LF(A7) = LS(B) = 35 dengan
nilai LS masing-masing adalah 32 (= 35 – 3) dan 33 (= 35 – 2). Kegiatan A6 dan A7 merupakan kegiatan penerus bagi kegiatan A5, sehingga LF(A5) = min{LS(A6), LS(A7)} = min{32 ; 33} = 32 dan LS(A5) adalah 25 (= 32 – 7). Selanjutnya pada kegiatan A5, hanya terdapat satu kegiatan pendahulu yaitu kegiatan A4, maka nilai LF(A4) = LS(A5) = 25 dan nilai LS(A4) adalah 24 (= 25 – 1). Begitu pula dengan kegiatan A4 yang hanya memiliki satu kegiatan pendahulu yaitu kegiatan A3, maka nilai LF(A3) = LS(A4) = 24 dengan nilai LS(A3) adalah 4 (= 24 – 20). Kegiatan A3 juga merupakan kegiatan penerus dari satu kegiatan yakni kegiatan A2, sehingga nilai LF(A2) = LS(A3) = 4 dengan nilai LS(A2) adalah 1 (= 4 – 3). Tiba pada kegiatan pertama yakni kegiatan A1. Kegiatan A2 merupakan kegiatan penerus bagi kegiatan A1, maka nilai LF(A1) = LS(A2) = 1 dan nilai LS(A1) adalah 0 (= 1 – 1).
Penentuan Jalur Kritis dengan Critical Path Method
Jalur kritis pada pelaksanaan proyek merupakan jalur yang apabila terlambat dapat mengakibatkan keterlambatan penyelesaian proyek secara keseluruhan (Wahyuni, 2011). Suatu jalur kritis bisa didapatkan dengan menambah waktu suatu aktivitas pada tiap urutan pekerjaan dan menetapkan jalur terpanjang pada tiap proyek. Kegiatan proyek dikatakan kritis apabila memiliki nilai slack = 0. Setelah melakukan analisis waktu optimal menggunakan perhitungan maju (forward pass) perhitungan mundur (backward pass), ditentukan nilai slack seluruh kegiatan dengan cara menghitung selisih antara earliest start (ES) dan latest start (LS) atau earliest finish (EF) dan latest finish (LF) dari aktivitas. Hasil perhitungan slack dan jalur kritis disajikan pada Tabel 2.
Tabel 2.
Perhitungan Nilai Slack dan Jalur Kritis Pada Proyek Pembangunan Perumahan Mutiara Residence
|
No |
Kode Durasi ES EF LS LF Slack Kritis / Tidak Kegiatan (hari) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
A1 1 0 1 0 1 0 Ya A2 3 1 4 1 4 0 Ya A3 20 4 24 4 24 0 Ya A4 1 24 25 24 25 0 Ya A5 7 25 32 25 32 0 Ya A6 3 32 35 32 35 0 Ya A7 2 32 34 33 35 1 Tidak B1 1 35 36 35 36 0 Ya B2 1 35 36 35 36 0 Ya C1 0.5 36 36,5 36 36,5 0 Ya C2 0.5 36 36,5 36 36,5 0 Ya D1 2 36,5 38,5 36,5 38,5 0 Ya D2 1.4 36,5 37,9 37,1 38,5 0,6 Tidak D3 0.5 36,5 37 38 38,5 1,5 Tidak D4 1 36,5 37,5 37,5 38,5 1 Tidak D5 0.5 36,5 37 38 38,5 1,5 Tidak E 2.5 38,5 41 38,5 41 0 Ya F 3.4 41 44,4 41 44,4 0 Ya G 3.1 44,4 47,5 44,4 47,5 0 Ya H 6.8 47,5 54,3 47,5 54,3 0 Ya I 14.5 54,3 68,8 54,3 68,8 0 Ya J 14.5 54,3 68,8 54,3 68,8 0 Ya K 3.3 54,3 57,6 65,5 68,8 11,2 Tidak L 6.5 68,8 75,3 68,8 75,3 0 Ya M 14.2 75,3 89,5 75,3 89,5 0 Ya N 2.8 75,3 78,1 93,6 96,4 18,3 Tidak O 6.9 89,5 96,4 89,5 96,4 0 Ya P 20.9 96,4 117,3 96,4 117,3 0 Ya Q 8.9 117,3 126,2 117,3 126,2 0 Ya R 6.5 117,3 123,8 119,7 126,2 2,4 Tidak S 6.9 126,2 133,1 126,2 133,1 0 Ya T 4.7 133,1 137,8 133,1 137,8 0 Ya U 4.9 117,3 122,2 132,9 137,8 15,6 Tidak V 2.9 137,8 140,7 137,8 140,7 0 Ya W 1.6 140,7 142,5 140,7 142,5 0 Ya |
Sumber: Data Diolah, 2018
Pada Tabel 2 terdapat 8 kegiatan yang bukan jalur kritis yaitu kegiatan A7, D2, D3, D4, D5, K, N, R, U. Artinya jika kegiatan-kegiatan tersebut mengalami keterlambatan, maka tidak akan mempengaruhi keterlambatan penyelesaian seluruh proyek. Melalui rangkaian kegiatan di atas yang memiliki lintasan sebagai
jalur kritis adalah lintasan A1-A2-A3-A4-A5-A6-B1-B2-C1-C2-D1-E-F-G-H-I-J-L-M-O-P-Q-S-T-V-W karena memiliki nilai slack = 0. Artinya, ketika kegiatan-kegiatan tersebut mengalami keterlambatan, maka akan menyebabkan keterlambatan penyelesaian seluruh proyek. Total waktu penyelesaian dari lintasan kritis di atas adalah 142,5 hari. Artinya penyelesaian seluruh rangkaian proyek dapat dilaksanakan minimal selama 142,5 hari.
Berdasarkan pembahasan tersebut, penjadwalan Proyek Pembangunan Perumahan Mutiara Residence dengan Critical Path Method (CPM) menunjukkan bahwa waktu pelaksanaan proyek dapat diselesaikan lebih cepat dibandingkan dengan hasil perhitungan oleh PT Putra Dewata Karya Tama dengan metode Gantt Chart. Pada penjadwalan yang dibuat oleh perusahaan memerlukan waktu 157 hari pengerjaan termasuk di dalamnya 37 hari pekerjaan persiapan dan 120 hari pekerjaan di lapangan, sedangkan berdasarkan hasil pembahasan dengan CPM, proyek dapat diselesaikan dalam kurun waktu 142,5 hari termasuk di dalamnya pekerjaan persiapan selama 37 hari dan pekerjaan di lapangan selama 105,5 hari. Jadi hasil perhitungan menggunakan CPM memberikan durasi penyelesaian lebih cepat 14,5 hari dari perhitungan sebelumnya yang tidak menggunakan CPM.
Hasil penelitian ini sesuai dengan hasil penelitian sebelumnya yang dilakukan oleh Wahyuni (2011), Elias and Ismail (2012), Sahid (2012), Syafridon dan Syahrizal (2013), Sugiarto dkk. (2013), Dharma (2013), Nugraha dan Marjono (2014), Anggriawan (2015), Permana dan Kholil (2016), Moghayedi, A. (2016), Nalhadi dan Suntana (2017), serta Purhariani (2017) menyatakan bahwa
dengan menggunakan Critical Path Method sebagai metode penjadwalan proyek, didapatkan perhitungan waktu penyelesaian proyek secara lebih efisien.
Biaya Total Proyek
Penentuan biaya total pelaksanaan proyek dihitung dengan menjumlahkan biaya langsung dan biaya tidak langsung. Menurut Husen (2010:113) komponen biaya langsung meliputi biaya material dan peralatan serta upah tenaga kerja langsung, sedangkan komponen biaya tidak langsung meliputi gaji, biaya pengadaan fasilitas sementara untuk bekerja, dan keperluan utility seperti listrik dan air. Perhitungan biaya total proyek adalah sebagai berikut.
Biaya Langsung = (Upah Tenaga Kerja per hari × Durasi Pelaksanaan Proyek) +
Biaya Material dan Peralatan
= (Rp. 1.435.000,00 × 105,5 hari) + Rp. 262,004,120.73
= Rp. 151.392.500 + Rp. 262.004.120,73
= Rp. 413.396.620,73
Biaya Tidak Langsung = (Gaji Tenaga Kerja + Biaya Listrik dan Air + Biaya KIPEM) per bulan × Durasi Pelaksanaan Proyek
= (Rp. 9.000.000 + Rp. 300.000 + Rp. 480.000 ) × 4 bulan
= Rp. 9.780.000 × 4 bulan
= Rp. 39.120.000
Total Biaya = Biaya Langsung + Biaya Tidak Langsung
Total Biaya = Rp. 413.396.620,73 +Rp. 39.120.000
= Rp. 452.516.620,73
Berdasarkan perhitungan tersebut, dihasilkan biaya total pelaksanaan proyek yang lebih kecil yaitu sebesar Rp. 452.516.620,73. Jadi dapat dikatakan bahwa penyelesaian proyek secara lebih cepat dapat berpengaruh terhadap biaya total pelaksanaan proyek secara keseluruhan. Pengurangan biaya terjadi pada biaya tenaga kerja dan biaya operasional yang dikeluarkan perusahaan, karena biaya tersebut berubah sesuai dengan waktu dan kemajuan proyek, semakin lama proyek berjalan maka semakin tinggi kumulatif biaya tidak langsung yang diperlukan (Soeharto, 1999:298).
IMPLIKASI HASIL PENELITIAN
Berdasarkan hasil penelitian, dengan menerapkan network planning menggunakan Critical Path Method (CPM) pada proyek pembangunan Perumahan Mutiara Residence, perusahaan dapat memperoleh efisiensi waktu dan biaya yang lebih besar dibandingkan dengan menggunakan metode Gantt Chart, karena metode Gantt Chart tidak dapat menunjukkan secara spesifik hubungan ketergantungan antar-kegiatan maupun kegiatan-kegiatan kritis pada pelaksanaan pembangunan proyek.
Berdasarkan data yang diperoleh dari PT Putra Dewata Karya Tama, proyek tersebut memerlukan waktu penyelesaian selama 157 hari yang meliputi 37 hari pekerjaan persiapan dan 120 hari pekerjaan di lapangan (Lampiran 3). Penjadwalan dengan metode jalur kritis memberikan durasi penyelesaian proyek lebih cepat dibandingkan dengan hasil perhitungan oleh perusahaan yakni sebesar 142,5 hari yang meliputi 37 hari pekerjaan persiapan dan 105,5 hari pekerjaan di
lapangan, sehingga efisiensi waktu penyelesaian proyek yang dapat diperoleh dengan Critical Path Method adalah sebesar 14,5 hari.
Berdasarkan data yang diperoleh dari PT Putra Dewata Karya Tama, proyek tersebut menghabiskan biaya total sebesar Rp.473.324.120,73 (Lampiran 6). Penyelesaian proyek secara lebih cepat berpengaruh terhadap total biaya pelaksanaan proyek seperti biaya tenaga kerja serta biaya operasional secara keseluruhan menjadi Rp. 452.516.620,73 sehingga efisiensi biaya yang dapat diperoleh dengan menggunakan Critical Path Method adalah sebesar Rp. 20.807.500.
SIMPULAN DAN SARAN
Berdasarkan hasil analisis data serta pembahasan yang telah dilakukan, maka dapat ditarik kesimpulan bahwa pada perencanaan jaringan kerja (network planning) proyek pembangunan Perumahan Mutiara Residence, terdapat 35 jenis pekerjaan (kegiatan) dimulai dari kegiatan persiapan sebelum pelaksanaan pembangunan sampai dengan pembangunan proyek benar-benar diselesaikan. Jalur kritis pada proyek pembangunan Perumahan Mutiara Residence berada pada lintasan A1-A2-A3-A4-A5-A6-B1-B2-C1-C2-D1-E-F-G-H-I-J-L-M-O-P-Q-S-T-V-W. Terdapat 26 kegiatan yang merupakan kegiatan kritis pada jalur kritis. Kegiatan-kegiatan tersebut memiliki kategori aktivitas kritis karena memiliki nilai slack = 0. Artinya jika kegiatan-kegiatan tersebut mengalami keterlambatan, maka akan menyebabkan keterlambatan penyelesaian seluruh proyek. Hasil perhitungan maju (forward pass) dan perhitungan mundur (backward pass) pada diagram jaringan dengan Critical Path Method menyatakan bahwa pelaksanaan seluruh
rangkaian proyek dapat diselesaikan selama 142,5 hari, termasuk di dalamnya 37 hari pekerjaan persiapan dan 105,5 hari pekerjaan di lapangan, sehingga efisiensi waktu yang dapat diperoleh adalah sebesar 14,5 hari. Biaya total yang dibutuhkan untuk proyek pembangunan Perumahan Mutiara Residence dengan perkiraan waktu menggunakan Critical Path Method adalah sebesar Rp. 452.516.620,73 dengan penghematan biaya yang dapat diperoleh yaitu sebesar Rp. 20.807.500.
Saran yang dapat diberikan berkaitan dengan penelitian ini sebagai bahan pertimbangan serta masukan yang berguna bagi PT Putra Dewata Karya Tama dimasa yang akan datang ialah PT Putra Dewata Karya Tama sebaiknya mempertimbangkan penerapan Network Planning dengan Critical Path Method pada sistem perencanaan, penjadwalan dan pengendalian proyek pembangunan, karena metode ini telah terbukti dapat membantu menentukan waktu optimal penyelesaian proyek dengan mengidentifikasi hubungan ketergantungan antar-kegiatan pelaksanaan proyek.
Perusahaan sebaiknya melakukan pengawasan pada pelaksanaan kegiatan-kegiatan kritis di mana kegiatan tersebut merupakan kegiatan yang apabila pelaksanaannya terlambat, maka akan menyebabkan keterlambatan bagi penyelesaian keselurruhan proyek. Penelitian selanjutnya dapat dilakukan menggunakan metode yang sama dengan menambahkan program percepatan (crashing program) pada perusahaan yang berbeda di mana pemilik proyek menginginkan adanya percepatan waktu dalam penyelesaian proyek untuk menentukan apakah penerapan Network Planning dengan Critical Path Method mampu mengefisienkan biaya pelaksanaan proyek.
REFERENSI
Adebowale, S. A. & Oluboyede, E. D. 2011. Network Analysis and Building Construction: Implications For Timing And Costing of Activities. Journal of Civil Engineering and Construction Technology, 2(5), pp. 90-100.
Adedeji, Adeola A. & Bello, Jimoh A. 2011. Construction of A Straw Bale Wallet Building – A Revew. International Journal of Engineering, 9(3), pp: 255262.
Anggriawan, Syahri dan Iskandar. 2015. Analisa Network Planning Reparasi KM Tonasa Line VIII Dengan Metode CPM Untuk Mengantisipasi Keterlambatan Penyelesaian Reparasi (Studi Kasus di PT. Dok dan Perkapalan Surabaya). Jurnal Teknik Mesin, 3(3), h: 106-111.
Badan Pusat Statistik, 2016. Konstruksi Dalam Angka 2016. Jakarta Pusat: Badan Pusat Statistik.
Badan Pusat Statistik, 2017. Provinsi Bali Dalam Angka Tahun 2017. Denpasar: BPS Provinsi Bali.
Dharma, Arief Adhi. 2013. Perencanaan Jaringan Kerja Pada Erection Block Kapal Untuk Meningkatkan Efisiensi Waktu Pembuatan (Studi Kasus di PT. Dok dan Perkapalan Surabaya). Jurnal Teknik Mesin, 1(2), h: 42 – 51.
Dimyati, H.A. Hamdan dan Nurjaman, Kadar. 2014. Manajemen Proyek, Cetakan Pertama. Bandung: Pustaka Setia.
Elias & Noriah Ismail. 2012. The Usage of Critical Path Method Software in Malaysian Construction. The International Journal of Knowledge, Culture And Change Management - Common Ground Publishing LLC, 11(5), pp: 1-17.
Ervianto, Wulfram I. 2004. Teori Aplikasi Manajemen Proyek Konstruksi, Salemba Empat, Yogyakarta.
Geraldi, Joana & Lechter, Thomas. 2017. Gantt Charts revisited: A critical analysis of its roots and implications to the management of projects today. International Journal of Managing Projects in Business, 5(4), pp: 578594.
Handoko, T. Hani. 2016. Dasar-Dasar Manajemen Produksi dan Operasi, Edisi 1. Yogyakarta: BPFE-Yogyakarta.
Heizer, Jay. dan Render, Barry. 2009. Manajemen Operasi, Edisi 9. Jakarta: Salemba 4.
Husen, Abrar. 2010, Manajemen Proyek. Yogyakarta: Andi Offset.
Moghayedi, A. 2016. Improving Critical Path Method (CPM) by Applying Safety Factor to Manage Delays. Scientia Iranica, 23(3), pp: 815-826.
Nalhadi, Ahmad dan Suntana, Nana. 2017. Analisa Infrastruktur Desa Sukaci-Baros Dengan Metode Critical Path Method (CPM). Jurnal Sistem dan Manajemen Industri, 1(1), h: 35-42.
Nugraha, Debby Paradita dan Marjono. 2014. Analisis Proyek Pengembangan Bangunan Menggunakan Critical Path Method dan Earned Value Method. Jurnal Mahasiswa Matematika, (2(4), h: 248-251.
Permana, Deni dan Kholil, Muhammad. 2016. Penjadwalan Waktu Proyek Contruction Civil Foundation Alfamart Dengan Menggunakan Critical Path Method (CPM). Spektrum Industri, 14(1), h: 1-108.
Pratasik, Failen. 2013. Menganalisis Sensitivitas Keterlambatan Durasi Proyek Dengan Metode CPM (Studi Kasus: Perumahan Puri Kelapa Gading). Jurnal Sipil Statik Universitas Sam Ratulangi, 1(9), h: 603-607.
Purhariani, Yerika. 2017. Penerapan CPM (Critical Path Method) Dalam Pembangunan Rumah. Simki-Economic, 1(5), h:1-13.
Rani, Hafnidar A. 2016. Manajemen Proyek Konstruksi, Edisi 1 Cetakan 1. Yogyakarta: Deepublish.
Risnawati dan Syahruni. 2014. Optimalisasi Pelaksanaan Proyek dengan Metode Evaluasi dan Review Proyek (PERT) dan Critical Path Method (CPM) Studi Kasus pada Proyek Renovasi Gedung Kantor Badan Penyelenggara Jaminan Sosial (BPJS) Ketenagakerjaan Cabang Sulawesi Tengah. Jurnal MSA, 3(2), h:57-63.
Sahid, Dadang Syarif Sihabudin. 2012. Implementasi Critical Path Method dan PERT Analysis pada Proyek Global Technology for Local Community. Jurnal Teknologi Informasi dan Telematika Politeknik Caltex Riau, 5(1), h: 14-22.
Santosa, Budi. 2009. Manajemen Proyek Konsep dan Implementasi, Cetakan
Pertama. Surabaya: Guna Widya.
Sha, Madan Kumar., Shahi, Padam Bahadur., Pandit, Ramananda., & Pandey, Ashok. 2017. Causes and Effects of Delays in Constrution Projets. IOSR Journal of Mechanical and Civil Engineering (IOSR-JMCE), 14(2), pp:52-58.
Soeharto, Imam. 1999. Manajemen Proyek (Dari Konseptual Sampai Operasional). Jakarta: Erlangga.
Syafridon, Gea Geby Aurora dan Syahrizal. 2013. Analisis Konsep Cadangan Waktu Pada Penjadwalan Proyek Dengan Critical Path Method (CPM) (Studi Kasus: Proyek Pembangunan Rumah Sakit Prima). Jurnal Teknik Sipil Universitas Sumatera Utara, 2 (1), h: 1055-1063.
Wahyuni, Sri Ngudi. 2011. Evaluasi Perencanaan Waktu Proyek Sistem Informasi Menggunakan Critical Path Method (Studi Kasus: Proyek Pengembangan Smart Graduate STMIK AMIKOM Yogyakarta). Jurnal Ilmiah Dasi, 15(4), h: 39-46.
Widiasanti, Irika dan Lenggogeni. 2013. Manajemen Konstruksi. Bandung: PT. Remaja Rosdakarya.
6758
Discussion and feedback