PENENTUAN PORTOFOLIO OPTIMAL DENGAN MENGGUNAKAN MODEL INDEKS TUNGGAL PADA SAHAM PERBANKAN DI BURSA EFEK INDONESIA

E-Jurnal Manajemen Unud, Vol. 5, No. 6, 2016: 3905-3933

ISSN : 2302-8912

PENENTUAN PORTOFOLIO OPTIMAL DENGAN MENGGUNAKAN MODEL INDEKS TUNGGAL PADA SAHAM PERBANKAN DI BURSA EFEK INDONESIA

Komang Nehru Utamayasa ¹

Ni Luh Putu Wiagustini ²

• ^1,2Fakultas Ekonomi dan Bisnis Universitas Udayana (Unud), Bali, Indonesia e-mail: [email protected]/ telp: +6281237674852

ABSTRAK

Penelitian ini bertujuan untuk mengetahui kombinasi dan proporsi portofolio optimal pada saham perbankan di Bursa Efek Indonesia dengan menggunakan model indeks tunggal, serta return dan risiko portofolio tersebut. Penelitian ini merupakan penelitian deskriptif kuantitatif. Penelitian ini menggunakan data sekunder. Populasi penelitian mencakup seluruh perusahaan perbankan yang terdaftar di BEI dengan menggunakan teknik sampling jenuh. Teknik pengumpulan data yang digunaan adalah observasi. Teknik analisis data yang digunakan pada penelitian ini adalah teknik analisis data deskriptif. Berdasarkan hasil analisis menunjukkan bahwa yang masuk ke dalam portofolio optimal dan besarnya proporsi dana adalah Bank Nusantara Pahrayangan Tbk dengan proporsi sebesar 69,58% dan Bank Himpunan Saudara Tbk dengan proporsi sebesar 30,42%.

Kata kunci: portofolio optimal, model indeks tunggal, sub sektor perbankan

ABSTRACT

This study aims to determine the optimal combination and proportion of the portfolio in banking shares on the Indonesia Stock Exchange using single index model, as well as the return and risk of the portfolio. This research is quantitative descriptive. This study uses secondary data. The study population includes the entire banking companies listed on the Stock Exchange by using sampling techniques saturated. Digunaan data collection techniques are observation. Data analysis techniques used in this research is descriptive data analysis techniques. Based on the results of the analysis indicate that the entry into the optimal portfolio and the large proportion of the funds are Pahrayangan Bank Nusantara Tbk with a proportion of 69.58% and the Bank Association of Brothers Tbk with a proportion of 30.42%.

Keywords: optimal portfolio, single index model, sub sector banking

PENDAHULUAN

Investasi di pasar modal secara global mengalami kemajuan cukup pesat.

Pasar modal juga menjalankan fungsi ekonomi dan keuangan di suatu negara.

Kemajuan perekonomian secara global menyediakan banyak kesempatan bagi investor untuk berinvestasi. Hal ini disebabkan meningkatnya keinginan masyarakat bisnis untuk mencari alternatif lain dalam mencari sumber pembiayaan usaha selain pinjaman bank. Pasar modal memungkinkan para investor mempunyai berbagai pilihan investasi yang sesuai dengan preferensi risiko. Perkembangan pasar modal juga dipengaruhi oleh meningkatnya kesadaran masyarakat untuk berinvestasi atau menjadi investor. Pada hakekatnya, tujuan investor melakukan kegiatan investasi adalah untuk mendapatkan hasil atas modal dari investasi yang dilakukannya. Namun, hampir semua investasi tentunya mengandung suatu ketidakpastian atau risiko. Investor tidak tahu dengan pasti return yang akan diperolehnya dari investasi yang dilakukan.

Pada umumnya, investor merupakan pihak yang tidak menyukai risiko tetapi menginginkan return yang maksimal. Investor menghadapi kesempatan investasi yang berisiko, pilihan investasi tentunya tidak dapat hanya mengandalkan pada tingkat keuntungan yang diharapkan. Untuk mendapatkan tingkat keuntungan yang tinggi, maka investor harus bersedia menanggung risiko yang tinggi pula.

Investor akan mendapat beberapa sumber return antara lain dari pembagian dividend dan capital gain yang merupakan selisih dari harga jual dan harga beli yang didapat oleh investor pada saat membeli saham tersebut. Hal ini mengharuskan investor mampu membuat analisis investasi sebelum menanamkan dananya. Peningkatan kemampuan analisis bagi para investor sangatlah penting disamping belum terjaminnya kemampuan manajer investasi dalam pengelolaan dana. Investor

dituntut mampu membentuk sendiri portofolio yang efisien pada berbagai instrumen investasi. Sebagai investor yang rasional yang perlu diperhatikan adalah meminimalkan risiko dengan cara melakukan diversifikasi.

Diversifikasi adalah menyusun suatu portofolio dengan menyertakan berbagai jenis investasi sehingga risiko dari portofolio berkurang, karena risiko dari salah satu saham dapat ditutup dengan keuntungan dari saham lain dalam portofolio tersebut. Persyaratan utama untuk dapat mengurangi risiko di dalam portofolio ialah return untuk masing-masing sekuritas tidak berkorelasi secara positif dan sempurna (Jogiyanto,2014 :338).

Analisis portofolio membantu investor dalam mengambil keputusan untuk menentukan portofolio efisien sehingga memberikan keuntungan yang besar dengan resiko tertentu atau memberikan resiko terkecil dengan tingkat keuntungan tertentu. Portofolio berarti sekumpulan investasi (Husnan,2003:45). Analisis portofolio merupakan identifikasi terhadap sekuritas-sekuritas mana yang akan dipilih dan berapa proporsi dana yang akan ditanamkan pada masing-masing sekuritas tersebut. Pemilihan jumlah sekuritas dimaksudkan untuk mengurangi risiko yang ditanggung. Sharpe (1963) mengembangkan model yang disebut dengan Model Indeks Tunggal. Model Indeks Tunggal ini dapat digunakan untuk menyederhanakan perhitungan di Model Markowitz dengan menyediakan parameter-parameter input yang dibutuhkan di dalam perhitungan Model Markowitz.

Dalam pembentukan suatu portofolio optimal terdapat dua Model yang dapat digunakan, yaitu Model Markowitz dan Model Indeks Tunggal. Perbandingan antara kedua model tersebut dapat dilihat dalam Tabel 1 berikut:

Tabel 1.

Perbedaan antara Model Markowitz dan Model Indeks Tunggal

Model Markowitz                         Model Indeks Tunggal

1.	Teori Markowitz didasari oleh tiga	1.	Model     ini    menghubungkan
	asumsi: - Periode investasi tunggal misalnya 1 tahun;	2.	perhitungan return setiap aset terhadap return indeks pasar Asumsi yang dipakai dalam Model
2.	-    Tidak ada biaya transaksi -    Preferensi investor hanya berdasar pada return harapan dan risiko. Belum           memperhitungkan	3.	ini adalah bahwa sekuritas akan berkorelasi hanya jika sekuritas-sekuritas tersebut mempunyai respon yang sama terhadap perubahan pasar Model ini merupakan
3.	kemungkinan     investor     untuk berinvestasi pada aset bebas risiko. Perhitungannya kompleks dan rumit.		penyerderhanaan dari Model perhitungan Markowitz yang kompleks.

Sumber: (Tandelilin, 2010: 132-162)

Berdasarkan Tabel 1 tersebut dapat diketahui bahwa Model Indeks Tunggal dibandingkan dengan Model Markowitz, Model Indeks Tunggal lebih sederhana serta mempertimbangkan aspek pasar dan aspek keunikan perusahaan, oleh sebab itu peneliti memilih Model Indeks Tunggal dalam pembentukan portofolio optimal. Model indeks tunggal dapat juga digunakan untuk menghitung return ekspetasi dan risiko portofolio. Pemilihan saham dan penentuan portofolio optimal yang dilakukannya didasari oleh pendahulunya Markowitz (1959) yang dimulai dari data historis atas saham individual yang dijadikan input, dan dianalisis untuk menjadikan keluaran yang menggambarkan kinerja setiap portofolio, apakah tergolong portofolio optimal atau sebaliknya.

Penelitian terdahulu yang meneliti mengenai pembentukan portofolio optimal berdasarkan Model Indeks Tunggal menunjukan hasil yang berbeda-beda. Andrade1 (2012) dalam penelitianya menunjukan hasil bahwa portofolio optimal dibentuk dari 5 perusahaan. Francis dan Rathika (2015) hasil penelitiannya menunjukan bahwa hanya satu Perusahaan yang dipilih untuk tujuan investasi yaitu Pharmaceutical companies. Naveen (2014) hasil penelitiannya menunjukan bahwa investor harus mengevaluasi portofolio dari waktu ke waktu untuk mendapatkan lebih banyak keuntungan, karena sifat volatile pasar dan ekonomi. Kamal (2012) hasil penelitiannya menunjukan bahwa membentuk portofolio saham dapat menguntungkan investor melalui diversifikasi dan pemanfaatan kombinasi pengembalian risiko yang berbeda. Banumathy dan Azhagaiah (2014) penelitiannya menunjukan bahwa sebuah portofolio saham dapat meningkatkan pengembalian dengan menyeimbangkan risiko antara sekuritas. Rajkumar dan Vinoth (2014) hasil penelitiannya menunjukan dari 5 perusahaan yang diambil untuk penelitian, kelima perusahaan tersebut membentuk portofolio optimal. Ramanathan dan Jahnavi (2014) hasil penelitiannya menunjukan bahwa terdapat 5 saham perusahaan yang memenuhi kriteria dalam pembentukan portofolio optimal.

Bursa efek menyediakan berbagai macam sektor dan sub sektor yang dapat dijadikan pilihan investasi oleh para investor, terutama dalam membentuk portofolio. Pada beberapa hasil penelitian sebelumnya, menunjukan kecenderungan investor dalam menanamkan dananya pada sektor manufaktur jika dibandingkan dengan sektor keuangan khususnya sub sektor perbankan. Analisis memprediksikan bahwa

sub sektor perbankan akan mampu mendatangkan keuntungan sehingga akan menarik minat bagi para investornya, hal ini didukung dengan melihat pesatnya perkembangan dunia perbankan saat ini. Sub sektor perbankan merupakan salah satu sub sektor yang sangat penting bagi suatu Negara dan juga sebagai jantung perekonomian suatu negara berada.

Pentingnya peran perbankan di suatu negara membuat saham perbankan begitu diminati oleh investor sehingga keberadaan perbankan akan berlangsung lama dan selalu berkembang dari waktu ke waktu. Karena begitu banyak individu maupun perusahaan yang akan selalu membutuhkan jasa perbankan. Alasan lain investor memilih saham perbankan adalah karena pengelolaan perbankan ini diawasi dan diatur oleh pemerintah yaitu Otoritas Jasa Keuangan (OJK) sehingga dunia perbankan ini akan selalu profesional dan transparan dalam mengelola dana masyarakat serta tentunya akan memberikan kepercayaan dan nilai positif di mata masyarakat.

Otoritas Jasa Keuangan (OJK) yang dibentuk berdasarkan Undang-undang No. 21 Tahun 2011 menjadi lembaga pengawas industri jasa keuangan yang terpercaya, melindungi kepentingan konsumen dan masyarakat, dan mampu mewujudkan industri jasa keuangan menjadi pilar perekonomian nasional yang berdaya saing global serta dapat memajukan kesejahteraan umum dengan melaksanakan tugas pengaturan dan pengawasan terhadap kegiatan jasa di sektor perbankan. Sepanjang tahun 2015 OJK memproyeksikan kredit di industri perbankan masih akan tumbuh di posisi 13%-15% sejalan dengan pertumbuhan laba bersih pada akhir tahun. Peningkatan kinerja perbankan terlihat dari hasil laba bersih pada Januari

– Mei tahun 2014 yaitu sebesar Rp 47,78 triliun, meningkat 11,90 % dari periode yang sama di tahun sebelumnya (OJK, 2014). Kondisi ini menunjukkan bahwa sub sektor perbankan layak untuk dijadikan sebagai salah satu pilihan investasi.

Beberapa penelitian sebelumnya yang mengkaji tentang pemilihan saham dan portofolio optimal telah banyak dilakukan oleh para peneliti terdahulu. Singh dan Gautam (2014) menggunakan Model Indeks Tunggal dalam pembentukan portofolio optimal di pasar saham India dengan asumsi kasus di mana short selling tidak diperbolehkan. Hasil penelitiannya menunjukan bahwa terdapat 2 perusahaan yang dipilih untuk tujuan investasi yaitu federal Bank Ltd, dan Yes Bank Ltd. Masing-masing total investasi dalam proporsi portofolio yaitu 97,51% dan 2,49% .

Francis dan Rathika (2015) meneliti mengenai portofolio optimal dengan menggunakan Model Indeks Tunggal di pasar saham India. Hasil penelitiannya menunjukan bahwa dari 10 perusahaan hanya 1 Perusahaan yang dipilih untuk tujuan investasi yaitu Pharmaceutical companies. Naveen (2014) dalam penelitiannya menerapkan Model Indeks Tunggal yang menunjukan hasil bahwa Sharpe memberi cara untuk membangun portofolio optimal. Investor harus mengevaluasi portofolio dari waktu ke waktu untuk mendapatkan lebih banyak keuntungan, karena sifat volatile pasar dan ekonomi.

Andrade1 (2012) dalam penelitianya menunjukan bahwa terdapat 5 perusahaan IT yang membentuk portofolio optimal. Mandal (2013) dalam penelitiannya yang bertujuan untuk membentuk sebuah portofolio optimal menggunakan Model Indeks Tunggal serta untuk menentukan return dan risiko

portofolio optimal. Hasil penelitiannya menunjukan bahwa pembentukan investasi portofolio optimal dengan menggunakan Model Indeks Tunggal lebih mudah dibandingkan dengan menggunakan Model Markowitz. Penelitian ini dilakukan atas dasar sampel kecil (n <30) yaitu 21 sekuritas sampel. Hal ini dapat diperluas untuk sampel besar untuk mendapatkan hasil yang lebih akurat.

Debasish dan Khan (2012) meneliti portofolio optimal menggunakan Model Indeks Tunggal pada saham manufaktur. Hasil penelitiannya menunjukan Dari 14 perusahaan yang diambil untuk penelitian, hanya 3 perusahaan yaitu Motor Hero Corp, Tata Motors dan Asian Paint yang termasuk dalam Portofolio Optimal.

Shah (2014) Hasil penelitiannya menunjukan bahwa pembentukan portofolio optimal dengan menggunakan Model Indeks Tunggal lebih efisien dan efektif dibandingkan dengan Model Markowitz. Kamal (2012) hasil penelitiannya menunjukan bahwa membentuk portofolio saham dapat menguntungkan investor melalui diversifikasi dan pemanfaatan kombinasi pengembalian risiko yang berbeda.

Banumathy dan Azhagaiah (2014) menganalisis kinerja portofolio dengan menggunakan Model Indeks Tunggal. Penelitiannya menunjukan bahwa sebuah portofolio efek dapat meningkatkan pengembalian dengan menyeimbangkan risiko antara sekuritas konstituen. Penelitian ini bertujuan untuk menganalisis hubungan antara beta portofolio dan pengembalian yang diharapkan.

Sarker (2013) penelitiannya menunjukan bahwa risiko dan return memainkan peran penting dalam membuat keputusan investasi. Dari 164 perusahaan yang diambil untuk penelitian, 7 perusahaan menunjukkan hasil negatif dan 157

perusahaan menunjukkan hasil yang positif. Studi ini menunjukkan bahwa portofolio beta secara signifikan lebih rendah dari beta pasar dan return portofolio jauh lebih tinggi dari varian portofolio.

Rajkumar dan Vinoth (2014) meneliti sebuah portofolio yang optimal di pasar saham India dengan menggunakan Model Indeks Tunggal. Hasil penelitiannya menunjukan dari 5 perusahaan yang diambil untuk penelitian, kelima perusahaan menunjukkan hasil yang positif. Nalini (2014), meneliti kegunaan Model Indeks Tunggal dalam pembentukan portofolio. Penelitiannya menunjukan di antara lima belas perusahaan yang menjadi sampel, hanya empat yang dipilih untuk portofolio optimal.

Ravichandra (2014) meneliti sebuah portofolio optimal dengan menggunakan Model Indeks Tunggal. Hasil penelitiannya menunjukan dari 50 perusahaan yang diambil, 6 perusahaan menunjukkan return negatif dan 44 perusahaan menunjukkan hasil yang positif. Ramanathan dan Jahnavi (2014) meneliti portofolio yang ideal dengan menggunakan Model Indeks Tunggal. Hasil penelitian menunjukan 5 saham yang memenuhi kriteria untuk dimasukkan dalam portofolio sesuai dengan Model Indeks Tunggal yaitu PVR, media HT, Sun TV, Saregama, pasar Dish pangsa TV.

METODE PENELITIAN

Penelitian ini merupakan penelitian deskriptif kuantitatif yang mendeskripsikan pembentukan model portofolio optimal dengan data yang diperoleh serta diolah dengan menggunakan rumus-rumus yang telah didapatkan dari beberapa

teori kemudian dianalisis dan dideskripsikan untuk kemudian dijadikan satu kesimpulan. Penelitian deskriptif adalah penelitian yang menggambarkan suatu fenomena berkaitan dengan populasi penelitian atau estimasi proporsi populasi yang mempunyai karakteristik tertentu (Cooper dan Emory, 1995).

Adapun hal-hal yang akan dideskripsikan dalam penelitian ini adalah Pembentukan portofolio optimal pada saham sub sektor perbankan yang menggunakan Model Indeks Tunggal. Dalam suatu pembentukan portofolio terdapat beberapa variabel yang diukur dan dideskripsikan, yaitu mengenai risiko dan return saham dari sub sektor perbankan. Selain itu, akan dideskripsikan mengenai proporsi masing-masing saham yang terbentuk dalam portofolio optimal dan tingkat expected return serta risiko dari portofolio optimal tersebut.

Penelitian ini dilakukan pada sub sektor perbankan yang terdaftar di Bursa Efek Indonesia (BEI) periode januari 2013- juli 2015 yang dapat diakses melalui www.idx.co.id. Objek dalam penelitian ini adalah saham sub sektor perbankan yang terdaftar di Bursa Efek Indonesia periode Januari 2013 – Juli 2015. Data diperoleh dari situs resmi Bursa Efek Indonesia, yaitu www.idx.co.id.

Variabel penelitian adalah suatu atribut atau sifat nilai dari orang, obyek atau kegiatan yang mempunyai variasi tertentu yang ditetapkan oleh peneliti untuk dipelajari dan dijadikan satu kesimpula (Sugiyono, 2013:58). Variabel yang di analisis dalam penelitian ini adalah portofolio optimal.

Menghitung nilai tingkat pengembalian (return) saham (Ri) masing-masing saham setiap bulannya dengan rumus Return realisasi yang dihitung menggunakan

data historis. Return realisasi atau return historis ini juga berguna sebagai dasar penentuan return dan risiko yang masa datang. Dengan rumus (Jogiyanto, 2014: 265)

P_t-'.

(1)

Dimana:

Ri = return realisasi saham

Pt = harga saham pada periode t

Pt-1 = harga saham pada periode t-1

Expected return atau tingkat pengembalian yang diharapkan dihitung dari rata-rata return realisasi saham dibagi dengan jumlah periode pengamatan, dengan rumus (Husnan, 2003:47):

ΣR

—..................................................................................(2)

τt

t=ι

Dimana:

E(Ri)  = expected return saham

Ri     = return realisasi saham

n     = jumlah periode pengamatan

Risiko saham adalah perbedaan antara expected return dan realized tersebut.

Risiko saham dapat dihitung dengan rumus (Zubir , 2011: 23):

n

√=-y‰-^)²

(3)

Dimana :

σ.^   = varian return saham

n = jumlah hari observasi

Rit   = return saham I pada hari ke t

E(Ri) = expected return saham ke i

Pemilihan dari indeks pasar tidak tergantung dari suatu teori tetapi lebih tergantung dari hasil empirisnya (Jogyanto,2014:408). Return indeks pasar memiliki nilai return indeks yang merupakan nilai keuntungan yang didapat para pelaku investor dalam melaksanakan perdagangan melalui IHSG. IHSG atau Indeks Harga Saham Gabungan merupakan bursa saham yang memiliki perhitungan saham yang sama dengan bursa saham lain diseluruh dunia. Jumlah nilai pasar pada IHSG merupakan keseluruhan perkalian dari tiap saham yang tercatat dalam hal ini terdapat pengecualian pada perusahaan yang tengah berada pada tahap restrukturisasi dengan harga BEI pada tanggal tersebut.

Menghitung return pasar (RM) periode januari 2013 - juli 2015 dengan rumus:

IHSG_c-IHSG_f

(4)

Dimana :

RM    = return pasar

IHSGt = indeks Harga Saham Gabungan periode t

IHSGt-1 = indeks Harga Saham Gabungan periode t-1

Return ekspektasi pasar atau tingkat yang diharapkan dari return pasar dihitung dari rata-rata indeks pasar dibagi dengan jumlah periode pengamatan, dengan rumus (Jogiyanto,2014:281):

E(R_m) = J R_m/,

(S)

Dimana :

E(RM) = expected return pasar

RM   = return pasar

n = jumlah periode pengamatan

Risiko pasar dapat dihitung dari selisih antara risiko pasar pada hari ke t dengan expected return pasar kemudian dibagi dengan jumlah periode pengamatan sebelumnya, dengan rumus :

Rmt ^^m)

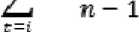
Dimana :

^σ⅛ = risiko pasar

^mt = risiko pasar pada hari ke t

E(M = expected return pasar n = jumlah periode pengamatan

Beta adalah parameter yang mengukur volalitas return saham terhadap return pasar. Sementara itu koefisien alpha suatu saham menunjukan bagian return yang unik yaitu return yang tidak dipengaruhi oleh kinerja pasar. Beta saham dapat dihitung dengan rumus (Jogiyanto, 2014:424) :

βι =≡………………………………………………………..…………(7)

α = E(R₁)-(P-E(R_m))……………………………………..………………….(8)

Dimana :

βi      = beta sekuritas

σiM = kovarian return sekuritas ke-i dengan return pasar

^σM    = varians return pasar

αi      = alpha sekuritas

E(Ri)  = expected return saham

RM    = return pasar

Varians dari kesalahan residu dapat dihitung dengan rumus :

⅛ =^_l²-βf^m ……………………………………………………………….(9)

Dimana :

⅛ = varians dari kesalahan residu

O⅛ = varians saham i

fit = beta sekuritas

^σM = varians return pasar

Menghitung tingkat pengembalian bebas risiko (RBR) menggunakan rata- rata

suku bunga SBI periode januari 2013 - juli 2015. Portofolio optimal berdasarkan

model indeks tunggal

ERB merupakan selisih antara expected return dan return aktiva bebas

risiko yang kemudian dibagi dengan beta, dengan rumus (Jogiyanto, 2014:430):

ERB. = ≡≡⅛……………………………..……………………….(10)

Dimana:

ERBi = excess return to Beta

E(Ri) = expected return saham

RBR   = return aktiva bebas risiko

βi      = beta sekuritas

Cut-off Rate (Ci) Merupakan titik pembatas untuk menentukan apakah suatu

saham dapat masuk ke dalam portofolio atau tidak. Saham-saham yang dimasukan ke

dalam portofolio merupakan saham yamg memiliki Ci ≤ ERB. Ci dihitung dengan

terlebih dahulu menghitung nilai Ai dan Bi untuk masing-masing sekuritas ke-I sebagai berikut (Jogiyanto, 2014:431):

°⅞¾ιl⅜ ι+⅛∑⅛

(11)

Dimana :

σ^ = varian dari return pasar

Sebelumnya dalam perhitungan rumus Ci perlu diketahui nilai Ai dan Bi dengan masing-masing rumusnya sebagai berikut:

_a =(E(Rj)-RBB)-Pi

(12)

(13)

si

Dimana :

^σei = varian dari kesalahan residu sekuritas ke-I yang juga merupakan risiko unik atau

risiko tidak sistematik

Proporsi sekuritas ke-I (Wi) merupakan proporsi dana masing-masing saham dalam portofolio, dihitung dengan rumus (Jogiyanto, 2014:435):

Z_i = ⅛ (ERB_j-C^………………………………………………….(14)

^^{i -} ∑∖∙ …………………………………………………………….(15)

Dimana:

Wi   = Proporsi sekuritas ke-i

Zi    = Suatu konstanta

k     = Jumlah sekuritas di portofolio optimal

βi     = Beta sekuritas

• *^    = Varians dari kesalahan residu

ERBi = Excess Return to beta

C* = Nilai cut-off point yang merupakan nilai terbesar

Risiko portofolio tidak merupakan rata-rata tertimbang dari seluruh risiko sekuritas tunggal (Jogyanto, 2014:313). Untuk menghitung risiko portofolio dapat

dihitung dengan rumus :

n                    n

⅛ =(Jw_i.β.)².o^+(^w_i.σ_ei)²

(16)

i=ι                        i=i

Dimana :

σ^            = Risiko portofolio

^σM _. ^f = Risiko yang berhubungan dengan pasar

Wi . C⅛      = Rata-rata tertimbang dari risiko unik masing-masing perusahaan

Return portofolio merupakan rata-rata tertimbang dari return individual masing-masing saham pembentuk portofolio, dapat dihitung dengan rumus (Jogiyanto, 2014:312):

nw

E(R_p)) = J’ w₁. α₁₊ J' w₁. P₁-E(R_m))(17)

t=(t=!

E(Rp) = Expected return portofolio βi = Beta sekuritas αi = Alpha sekuritas

E(RM) = Expected return pasar

Peneliti menggunakan jenis data sekunder dalam penelitian ini. Data sekunder adalah data yang sudah tersedia sehingga tinggal mencari dan mengumpulkannya (Sarwono, 2008:153). Data sekunder tersebut meliputi daftar perusahaan sub sektor perbankan yang termasuk dalam periode januari 2013 – juli 2015.

Populasi adalah keseluruhan dari subjek penelitian (Arikunto, 2010:173). Populasi pada penelitian ini adalah seluruh perusahaan yang terdaftar dalam sub sektor perbankan yang aktif diperdagangkan selama periode januari 2013 - juli 2015 yaitu sejumlah 28 saham perbankan. Sampel adalah sebagian atau wakil populasi yang diteliti (Arikunto, 2010:174). Teknik yang digunakan dalam pengambilan sampel di dalam penelitian ini adalah sampling jenuh (sensus). Teknik penarikan sampel ini dimana semua anggota populasi dijadikan sebagai sampel yaitu saham perusahaan perbankan yang masih aktif diperdagangkan selama periode januari 2013 - juli 2015.

Teknik pengumpulan data yang digunakan dalam penelitian ini adalah observasi. Observasi merupakan cara pengumpulan data dengan melihat dan menggunakan dokumen yang berkaitan dengan tema penelitian. Teknik observasi yang digunakan dalam penelitian ini adalah dengan cara mengumpulkan data sekunder yang telah dipaparkan sebelumnya.

Teknik analisis data yang digunakan pada penelitian ini adalah teknik analisis data deskriptif. Langkah-langkah yang dilakukan dalam pembentukan portofolio optimal dengan menggunakan model indeks tunggal berdasarkan data yang dikumpulkan adalah sebagai berikut (1) Menghitung return masing-masing saham perbankan serta return pasar. (2) Menghitung expected return masing-masing saham perbankan serta expected return pasar. (3) Menghitung varians pasar. (4) Menghitung beta dan alpha masing-masing saham perbankan. (5) Menghitung risiko sistematis dan varians dari kesalahan residu. (6) Menentukan tingkat pengembalian bebas risiko

(RBR) menggunakan rata-rata suku bunga SBI periode januari 2013 - juli 2015. (7) Menghitung Excess return to beta (ERB). (8) Mengurutkan peringkat saham perbankan berdasarkan Excess return to beta (ERB) yang terbesar sampai yang terkecil. (9) Menghitung Cut-off Rate (Ci). (10) Menghitung Cut-off Point (C*). (11) Menentukan kandidat portofolio optimal dengan menggunakan kriteria jika ERB saham ≥ C*. (12) Menghitung proporsi masing-masing saham perbankan. (13) Menghitung expected return dan varians yang selanjutnya digunakan untuk menghitung risiko portofolio.

HASIL DAN PEMBAHASAN

Dalam perhitungan portofolio, data yang digunakan adalah nilai yang terjadi di pasar modal yaitu harga saham perbankan, harga indeks pasar, dan tingkat suku bunga SBI, sedangkan input portofolionya adalah nilai-nilai yang dibutuhkan untuk menghitung portofolio optimal. Penentuan portofolio optimal disajikan berikut ini dilengkapi dengan tahapan-tahapannya (a) Memasukan nilai return bebas risiko (RBR) yang diperoleh dari rata-rata tingkat suku bunga SBI selama periode pengamatan yaitu sebesar 0,0667. (b) Menghitung expected return dengan mencari nilai rata-rata return saham masing-masing perusahaan. (c) Mencari deviasi standar return saham masing-masing perusahaan (Varian return saham). (d) Return pasar (Rm) dihitung rata-rata historis return pasasr diperoleh nilai sebesar 0,033184. (f) Menghitung deviasi standar return pasar (varian return pasar) diperoleh nilai sebesar 0,1821. (g) Mencari beta dengan menghitung kovarian return aktiva dengan return pasar dibagi dengan varian atau deviasi standar pasar yang dikuadratkan. (h) Alpha

dihitung dengan expected return dikurang Beta kemudian dikalikan return pasar. (i) Menghitung risiko unik dengan cara mengurangi risiko total dengan Beta kemudian dikalikan dengan varian pasar. (j) Excess Return to beta atau ERBi dengan cara kelebihan expected return dari return bebas risiko dibagi dengan beta untuk masing-masing aktiva.

Hasil perhitungan di atas yaitu masing-masing emiten dapat dirangkum dan ditunjukan pada tabel berikut.

Tabel 1.

Rekapitulasi Expected Return, Deviasi Standar, Beta, Alpha, Risiko Unik, dan Excess Return to beta masing-masing Emiten

No.	Emiten	E(Ri)	σi              βi		αi	2 βei	ERBi
1.	BABP	-0,02751	0,099987	0,193854	-0,03394	0,008751	-0,48753
2.	BACA	0,00728	0,129257	0,095076	0,004125	0,016408	-0,62812
3.	BBCA	0,008253	0,061278	0,096112	0,005063	0,003449	-0,61124
4.	BBKP	-0,00884	0,111656	0,114431	-0,01263	0,012033	-0,66273
5.	BBNI	0,001746	0,099197	0,184989	-0,00439	0,008705	-0,35275
6.	BBNP	0,017502	0,053315	-0,01174	0,017892	0,002838	4,215993
7.	BBRI	0,003725	0,089781	0,174807	-0,00208	0,007047	-0,36197
8.	BBTN	-0,01555	0,097264	0,139072	-0,02016	0,008819	-0,59355
9.	BDMN	-0,01687	0,097235	0,176031	-0,02271	0,008427	-0,47645
10.	BEKS	-0,02761	0,090213	0,013296	-0,02805	0,008133	-7,11549
11.	BJBR	-0,01797	0,098875	0,253274	-0,02637	0,007649	-0,33548
12.	BJTM	0,001727	0,096439	0,12853	-0,00254	0,008753	-0,50784
13.	BKSW	-0,03895	0,1858	0,01597	-0,03948	0,034513	-6,63455
14.	BMRI	-0,00132	0,080036	0,166615	-0,00685	0,005485	-0,41007
15.	BNBA	-0,00219	0,067317	0,015985	-0,00273	0,004523	-4,32868
16.	BNGA	-0,02212	0,064448	0,030284	-0,02313	0,004123	-2,94298
17.	BNII	-0,02655	0,055678	0,033637	-0,02766	0,003063	-2,78108
18.	BNLI	0,001101	0,062613	0,105558	-0,0024	0,003551	-0,62429
19.	BSIM	0,015449	0,054064	0,128503	0,011185	0,002375	-0,40116
20.	BSWD	-0,07852	0,524465	0,22858	-0,08611	0,273331	-0,63664
21.	BVIC	-0,00241	0,049729	0,025195	-0,00325	0,002452	-2,75513
22.	INPC	-0,0133	0,0429	0,052034	-0,01503	0,001751	-1,54319
23.	MAYA	-0,05536	0,246888	0,328144	-0,06625	0,057383	-0,37289
24.	MCOR	0,004592	0,105011	0,166944	-0,00095	0,010103	-0,37382
25.	MEGA	-0,044	0,338993	0,127483	-0,04823	0,114377	-0,87067
26.	NISP	-0,00782	0,058895	0,031872	-0,00888	0,003435	-2,34756
27.	PNBN	0,009794	0,107982	0,099872	0,00648	0,011329	-0,57279

7

No. Emiten     E(Ri)        σi          βi          αi__________¾        ERBi

28. SDRA 0,017347   0,082153    -0,03442    0,01849     0,00671   1,442359

Sumber : data sekunder diolah, 92015)

Berdasarkan Tabel 1 dapat dilihat bahwa saham yang memiliki expected return E(Ri) yang positif terdapat 11 saham yaitu BACA, BBCA, BBNI, BBNP,BBRI, BJTM, BNLI, BSIM, MCOR, PNBN, dan SDRA, sedangkan expected return E(Ri) yang negatif terdapat 17 saham yaitu BABP, BBKP, BBTN, BDMN, BEKS, BJBR, BKSW, BMRI, BNBA, BNGA, BNII, BSWD, BVIC, INPC, MAYA, MEGA, NISP. Expected return tertinggi terdapat pada saham BNNP sebesar 0,017502, sedangkan expected return terendah terdapat pada saham BSWD sebesar -0,07852. Hal ini menunjukan bahwa expected return bernilai positif berarti saham tersebut layak untuk dipertimbangkan dalam berinvestasi karena expected return merupakan return yang diharapkan dari suatu investasi. Risiko tertinggi terdapat pada saham BSWD sebesar 0,524465, sedangkan risiko terendah pada saham INPC sebesar 0,0429.

Beta individual aktiva (βi) merupakan kovarian masing-masing aktiva dengan return pasar dibagi dengan deviasi standar pasar yang dikuadratkan sehingga menghasilkan nilai Beta masing-masing aktiva pada Tabel 1. Beta tertinggi terdapat pada saham MAYA sebesar 0,328144 sedangkan Beta terendah pada saham SDRA sebesar -0,03442. Alpha individual aktiva merupakan expected return dikurang Beta kemudian dikalikan expected return pasar sehingga menghasilkan nilai Alpha masing-masing aktiva yang ditunjukan pada Tabel 4.1 Alpha tertinggi terdapat pada

saham SDRA sebesar -0,03442, sedangkan Alpha terendah pada saham BSWD sebesar -0,08611.

Risiko unik ( ^σs; ) diperoleh dari risiko total dikurangi Beta kemudian dikalikan dengan deviasi standar pasar yang hasilnya ditunjukan pada Tabel 1. Risiko unik tertinggi terdapat pada saham MEGA sebesar 0,11437, sedangkan risiko unik terendah pada saham INPC sebesar 0,00175. Excess return to beta (ERB) merupakan selisih dari expected return dengan return bebas risiko kemudian dibagi Beta. Excess return to beta (ERB) menunjukan nilai kinerja dari aktiva yaitu hubungan antara expected return dan risiko. Berdasarkan Tabel 4.1 terlihat bahwa expected return tertinggi terdapat pada saham BBNP sebesar 4,215993, sedangkan expected return terendah pada saham BEKS sebesar -7,11549.

Portofolio yang optimal terbentuk dari aktiva-aktiva yang mempunyai nilai rasio ERB yang tinggi yang ditentukan berdasarkan titik pembatas (Cut-off point). Langkah-langkah dalam menentukan aktiva-aktiva yang masuk dalam portofolio optimal tersebut adalah sebagai berikut: Mengurutkan aktiva-aktiva berdasarkan nilai ERB terbesar ke nilai ERB terkecil. Aktiva-aktiva dengan nilai ERB terbesar merupakan kandidat untuk dimasukan ke portofolio optimal. Menghitung nilai Ci dengan langkah sebagai berikut: (a) Hitung Aj (bagian dari Ci dalam rumus) dengan cara mengurangi nilai expected return masing-masing aktiva dengan return bebas risiko kemudian dikalikan dengan Beta dan dibagi dengan risiko unik. (b) Setelah diperoleh masing-masing nilai Aj, selanjutnya dengan menjumlahkan nilai Aj dari

nilai-nilai Aj sebelumnya (ƩAj). (c) Hitung Bj (bagian dari Ci dalam rumus) dengan cara mengkuadratkan Beta kemudian dibagi dengan risiko unik. (d) Setelah diperoleh masing-masing nilai Bj, selanjutnya menjumlahkan nilai Bj dari nilai-nilai Bj sebelumnya (ƩBj). (f) Menghitung nilai Ci dengan mengkuadratkan varian return pasar dikalikan ƩAj kemudian dibagi satu ditambah varian return pasar dikuadratkan dikalikan ƩBj. Dari hasil Ci dapat ditentukan nilai C* yang merupakan cut-off yang memasukan aktiva-aktiva ke dalam portofolio optimal. Letak nilai C* adalah nilai Ci tertinggi.

Hasil perhitungan diatas yaitu untuk mencari titik pembatas (cut-off point) yang akan digunakan untuk menentukan berapa batas nilai ERB yang dikatakan tinggi. Hasil perhitungan dapat dirangkum pada tabel berikut.

Tabel 2.

Hasil Perhitungan Titik Pembatas (cut-off point) pada portofolio optimal
No.	EMITEN	ERBi	Aj	ƩAj	Bj	ƩBj	Ci
1.	BBNP	4,215993	0,204772	0,575037	0,04857	6,951884	0,015497
2.	SDRA I	1,442359I	0,254739	0,829776	0,176613	7,128497 ■	0,022256I
3.	BJBR	-0,33548	-2,81353	-1,98375	8,386539	15,51504	-0,04344
4.	BBNI	-0,35275	-1,38669	-3,37044	3,9311	19,44614	-0,06795
5.	BBRI	-0,36197	-1,56954	-4,93997	4,336125	23,78226	-0,09159
6.	MAYA	-0,37289	-0,69972	-5,6397	1,876492	25,65875	-0,10104
7.	MCOR	-0,37382	-1,03122	-6,67092	2,758575	28,41733	-0,11389
8.	BSIM	-0,40116	-2,78883	-9,45975	6,951884	35,36921	-0,14437
9.	BMRI	-0,41007	-2,07534	-11,5351	5,060958	40,43017	-0,16342
10.	BDMN	-0,47645	-1,75195	-13,287	3,677076	44,10725	-0,17892
11.	BABP	-0,48753	-2,09352	-15,3806	4,294178	48,40142	-0,19579
12.	BJTM	-0,50784	-0,95852	-16,3391	1,887435	50,28886	-0,20311
13.	PNBN	-0,57279	-0,5043	-16,8434	0,880414	51,16927	-0,20711
14.	BBTN	-0,59355	-1,30175	-18,1451	2,193165	53,36244	-0,21726
15.	BBCA	-0,61124	-1,63726	-19,7824	2,678589	56,04103	-0,2295
16.	BNLI	-0,62429	-1,95901	-21,7414	3,137961	59,17899	-0,24337
17.	BACA	-0,62812	-0,34606	-22,0875	0,550938	59,72993	-0,24573
18.	BSWD	-0,63664	-0,1217	-22,2092	0,191156	59,92108	-0,24656
19.	BBKP	-0,66273	-0,7212	-22,9303	1,088227	61,00931	-0,25153
20.	MEGA	-0,87067	-0,12371	-23,0541	0,14209	61,1514	-0,25249
21.	INPC	-1,54319	-2,38676	-25,4408	1,546635	62,69803	-0,27399

No.	EMITEN	ERBi	Aj	ƩAj	Bj	ƩBj	Ci
22.	NISP	-2,34756	-0,69427	-26,1351	0,295742	62,99378	-0,28057
23.	BVIC	-2,75513	-0,71327	-26,8484	0,258889	63,25266	-0,28743
24.	BNII	-2,78108	-1,02744	-27,8758	0,36944	63,6221	-0,29726
25.	BNGA	-2,94298	-0,65459	-28,5304	0,222423	63,84453	-0,30352
26.	BNBA	-4,32868	-0,24454	-28,7749	0,056493	63,90102	-0,30593
27.	BKSW	-6,63455	-0,04902	-28,824	0,007389	63,90841	-0,30643
28.	BEKS	-7,11549	-0,15467	-28,9786	0,021737	63,93015	-0,308

Sumber : data sekunder diolah, (2015)

Pada Tabel 2 terlihat bahwa nilai Ci dari saham-saham tersebut yang terbesar adalah nilai Ci dari saham Bank Himpunan Saudara Tbk.(SDRA) yaitu sebesar 0,022256, Sehingga cut off point (C*) dari saham-saham yang akan membentuk portofolio adalah 0,022256. Selanjutnya setelah nilai C* ditentukan, maka dilakukan pemilihan saham-saham yang dapat dijadikan kandidat untuk membentuk portofolio optimal dengan cara membandingkan nilai dari ERB masing-masing saham dengan nilai C*. Dari Tabel 2 dapat terlihat bahwa saham perusahaan yang memiliki nilai ERB yang lebih besar dari C* adalah BBNP dan SDRA. Oleh karena itu saham-saham tersebut dapat dimasukan dalam kandidat saham untuk dapat membentuk portofolio optimal.

Setelah menentukan aktiva-aktiva mana yang membentuk portofolio optimal, selanjutnya menghitung proporsi dana masing-masing aktiva di portofolio optimal dengan cara: 1) Hitung nilai Zi dengan membagi Beta dengan risiko unik kemudian dikalikan denga selisih nilai ERBi dengan cut-off point. 2) Hitung proporsi masing-masing saham yaitu Zi dibagi dengan total ƩZi. Hasil perhitungan dalam penentuan proporsi dana yang dialokasikan pada masing-masing aktiva dalam portofolio optimal dapat dilihat pada tabel 3.

Tabel 3.

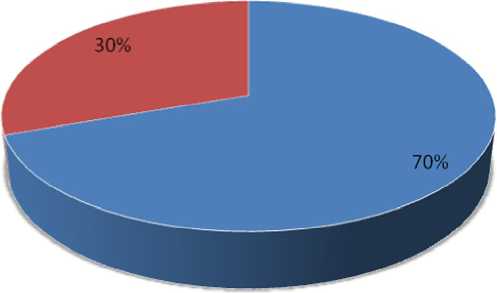
Proporsi Dana Masing-masing Aktiva portofolio Optimal No. Aktiva Zi        Wi Proporsi

■ BBNP BSDRA

1.	BBNP	-17,722	0,695791	69,58%
2.	SDRA	-7,748	0,304208	30,42%

Total       100%

Sumber : data sekunder diolah, (2015)

Gambar 1. Proporsi Masing-masing Aktiva Portofolio Optimal

Sumber : data sekunder diolah, (2015)

Dari Tabel 3 menunjukan bahwa proporsi terbesar dalam pengalokasian dana pada portofolio optimal adalah Proporsi saham BBNP (Bank Nusantara Pahrayangan Tbk) yaitu sebesar 69,58%, sedangkan proporsi terkecil dalam pengalokasian dana pada portofolio optimal adalah Proporsi saham SDRA (Bank Himpunan Saudara Tbk) yaitu sebesar 30,42%.

Tahap terakhir dalam proses perhitungan portofolio optimal, yaitu menghitung besarnya expected return dan risiko portofolio optimal. Expected return portofolio adalah tingkat pengembalian yang diharapkan dari portofolio yang dibentuk. Sebelum expected return portofolio dihitung terlebih dahulu menghitung beta portofolio dan alpha portofolio.

Tabel 4.

Portofolio Optimal

αp βp Risiko sitematis Total Risiko E(Rp)

0,01807 -0,01864 0 0,002 0,01805

Dari Tabel 4 dapat menunjukan bahwa nilai return portofolio adalah 0,0180 atau 1,8% sedangkan nilai risiko portofolio adalah 0,0020 atau 0,02%. Artinya dari portofolio yang terbentuk mampu menghasilkan return ekspektasi sebesar 1,8% dengan risiko terendah sebesar 0,02%. Hasil tersebut menunjukkan besarnya return ekpektasi yang akan dihasilkan lebih besar dari nilai risiko sebesar 0,02%. Berdasarkan hasil tersebut maka dapat dikatakan portofolio ini merupakan portofolio yang optimal serta layak menjadi pertimbangan investor.

SIMPULAN DAN SARAN

Berdasarkan hasil penelitian maka dapat ditarik simpulan bahwa saham-saham yang dapat dimasukan dalam penentuan portofolio optimal dengan menggunakan

model indeks tunggal pada sub sektor saham perbankan selama periode januari 2013 sampai dengan juli 2015 beserta proporsinya terdiri atas dua saham, yaitu : BBNP (Bank Nusantara Pahrayangan Tbk) yaitu sebesar 69,58%, dan SDRA (Bank Himpunan Saudara Tbk) yaitu sebesar 30,42%. Tingkat keuntungan (expected return) portofolio sebesar 1,8% dengan risiko terendah sebesar 0,02%.

Berdasarkan hasil analisis dan simpulan, beberapa saran yang dapat diberikan adalah supaya dibentuk dengan beberapa portofolio optimal lagi dengan menggunakan model indeks tunggal pada sektor atau indeks saham lainnya di Bursa Efek Indonesia serta untuk dilakukan pengukuran dan membandingkan kinerja masing-masing portofolio optimal yang terbentuk. Kekurangan penelitian ini adalah hanya menggunakan sub sektor saham perbankan, untuk penelitian selanjutnya disarankan agar menggunakan sektor lainnya. Untuk penelitian sejenis berikutunya sebaiknya dilakukan penyesuaian dengan data terkini pada sub sektor saham perbankan.

REFERENSI

Arikunto, Suharsimi. 2010. Prosedur Penelitian: Suatu Pendekatan Praktek.

Jakarta: PT Rineka Cipta.

Bangun, Deddy H, Samuel P. D. Anantadjaja, Laura Lahindah. 2012. Portofolio Optimal Menurut Markowitz Model dan Single Index Model: Studi Kasus pada Indeks LQ45. Journal of Management Studies, 1(1): h: 70-93.

Bungin, Burhan. 2005. Metode Penelitian Kuantitatif. Jakarta: Gramedia Pustaka.

Ch. Naveen. 2014. Application of Sharpe Single Index Model to BSE. International

Journal of Management Studies, 4(2), pp: 1-5.

Fajarayu Rahmasita, R. Rustam Hidayat, Devi Farah. 2014. Pembentukan portofolio optimal dengan menggunakan Single index model : Studi Kasus pada saham-saham sektor industri dasar dan kimia bursa efek indonesia periode 20112013. Jurnal Administrasi Bisnis, 16(1): h: 1-10

Hartono, Jogiyanto. 2010. Teori Portofolio dan Analisis Investasi. Edisi Ketujuh. Yogyakarta: BPFE.

Husnan, Suad. 2009. Dasar-dasar Teori Portofolio & Analisis Sekuritas. Edisi Keempat. Yogyakarta: UPP STIM YKPN.

Islami, Nisma. 2010. Analisis Perbandingan Kinerja Portofolio Optimal Saham JII dengan Kinerja Portofolio Optimal Saham LQ 45. Jurnal Fakultas Ekonomi Universitas Islam Indonesia.

Javed Bin Kamal. 2012. Optimal Portfolio Selection In Ex Ante Stock Price Bubble And Furthermore Bubble Burst Scenario From Dhaka Stock Exchange With Relevance To Sharpe’s Single Index Model. Research Paper at SSRN.

Julianti, Elvida. 2009. Analisis Pembentukan Portofolio Optimal Pada Tiga Perusahaan dengan Menggunakan Teori Portofolio (Studi Kasus pada Saham PT. Gudang Garam Tbk, Saham PT HM Sampoerna Tbk, dan Saham PT Timah Tbk). Jurnal Fakultas Ekonomi Universitas Gunadarma.

Jogiyanto, 2014. Teori Portofolio dan Analisis Investasi. Edisi Kesembilan. Yogyakarta: Penerbit BPFE.

Karunanithy Banumathy and Ramachandran Azhagaiah. 2014. Portfolio Risk And Returns: Single Index Model of BSE. International Journal Of Information, Business And Management, 6(3), pp: 146-157.

K.V.Ramanathan and K.N. Jahnavi. 2014. Constructionof Optimal Equity Portfolio Using The Sharpe Indexmodel With Reference To Banking And Informationtechnologysectors In India From2009-2013. International Journal Of Business And Administration Research Review, 2(3), pp: 122-131.

Mary,J. Francis and Rathika G. 2015. The Single Index Model and The Construction Of Optimal Portfolio With Cnxpharma Scrip. International Journal Of Management (Ijm), 6(1), pp: 87-96.

Mokta Rani Sarker. 2013.Optimal Portfolio Construction: Evidence from Dhaka Stock Exchange in Bangladesh. World Journal of Social Sciences, 3(6), pp: 75 – 87.

Niranjan Mandal. 2013. Sharpe’s Single Index Model And Its Application To Construct Optimal Portfolio: An Empirical Study. An initiative of Yale-Great Lakes Center for Management Research, 7(1), pp: 01-22.

Otoritas Jasa Keuangan. 2014. Kinerja Bank: Perbankan Nasional Raih Laba Rp47,78 Triliun. http://ruangpojok.com/articles/berita/ekonomi/bank-bumn-torehkan-laba-rp-2123-triliun.html. Diunduh tanggal 19, bulan November, tahun 2014.

Otoritas Jasa Keuangan. 2015. OJK: Tekanan Laba Industri Perbankan berlanjut di paruh Ke 2.   http://m.tempo.co./read/news/2015/08/10/087690701/ojk-

tekanan-laba-perbankan-berlanjut-di-paruh-ke-2.html. Diunduh tanggal 16, bulan September, tahun 2015.

Pratibha Jenifer Andrade1. 2012. Construction Of Optimal Portfolio Of Equity, Using Sharpe’s Single Index Model: A Case Study Of It Sector. International Journal of Applied Financial Management Perspectives, 1(2), pp: 86-88.

Provita, Viola Claudia. 2012. Analisis Portofolio Optimal Investasi Saham yang Tercatat Sebagai Indeks LQ 45 Pada Bursa Efek Indonesia dengan Model Indeks Tunggal (Periode 2009-2011). Jurnal Fakultas Ekonomi Universitas Gunadarma.

Reilly, Frank K. and Keith C.Brown. 2003. Investment Analysis and Portfolio Management, Seventh Edition, The Dryden Press, New York.

Ria Rahmadin, Topowijono, Zahroh Z.A. 2014. Pembetukan Portofolio Optimal Saham berdasarkan Model Indeks Tunggal: Studi pada Saham Indeks LQ-45 di BEI Tahun 2011-2013. Jurnal Administrasi Bisnis (JAB), 9(2), pp: 1-8.

R.Nalini. 2014.Optimal Portfolio Construction Using Sharpe’s Single Index Model -A Study Of Selected Stocks From Bse. International Journal Of Advanced Research In Management And Social Sciences, 3(12), pp: 72-93.

Robi. 2008. Analisis Portofolio Optimal Saham-saham LQ-45 Pada Periode Agustus 2005-Juli 2006 dengan metode single indeks model di bursa efek jakarta. Business management Journal Bunda Mulia, 4(1).

R.Rajkumar and S.Vinoth. 2014. Optimal Portfolio Construction In Stock Market – An Empirical Study On Selected Stocks (Bse) Of automobile Companies.Intercontinental Journal Of Finance, 3(10), pp: 32-37.

Sathya Swaroop Debasish and Jakki Samir Khan. 2012. Optimal Portfolio Construction in Stock Market-An Empirical Study on Selected Stocks in Manufacturing Sectors of India. International Journal of Business Management, 2(2), pp: 37-44.

Saurabh Singhand Jayant Gautam. 2014. The Single Index Model & The Construction Of Optimal Portfolio: A Case Of Banks Listed On Nse India. Risk governance & control: financial markets & institutions, 4, pp: 110-115.

Sugiyono. 2001. Metode Penelitian Bisnis. Alfabeta. Bandung

Sulistyowati, Nurul. 2012. Analisis Pembentukan Portofolio Optimal Menggunakan Model Indeks Tunggal untuk Pengambilan Keputusan Investasi (Studi Kasus Saham LQ 45 di BEI Periode Agustus 2008-Januari 2011). Jurnal Fakultas Ekonomika dan Bisnis Universitas Diponegoro.

Tandelilin, Eduardus. 2010. Portofolio dan Investasi: Teori dan Aplikasi. Edisi Pertama. Yogyakarta: Kanisius.

Thangjam Ravichandra. 2014. Optimal Portfolio Construction With Nifty Stocks. International Journal of Interdisciplinary and Multidisciplinary Studies (IJIMS), 1(4), pp: 75-81.

Tirtana, Dodi. 2009. Analisis Portofolio Optimal Investasi Saham Pada Sektor Perbankan Di Bursa Efek Indonesia Studi Kasus (2006-2008). Jurnal Fakultas Ekonomi Universitas Gunadarma.

Tirthank Shah. 2014. Constructing Optimal Portfolio: Sharpe’s Single Index Model. Research Paper at SSRN.

Tushar Sen. 2010. Constructing an Optimal Portfolio With and Without Short Selling Using Single Index Model. Research Paper at SSRN.

Wiagustini, Ni Luh Putu. 2010. Dasar-dasar Manajemen Keuangan. Denpasar:Udayana University Press.

Winarto, Elthon Machael. 2007. Strategi Portofolio Optimal Menggunakna Single Indeks Model Saham-Saham LQ 45 di BEJ Periode 2002-2005. Jurnal Fakultas Ekonomi Universitas Gajah Mada.

Zubir, Zalmi. 2011. Manajemen Portofolio: Penerapannya dalam Investasi Saham. Jakarta: Salemba Empat.

3933