Comparing Support Vector Machine and Naïve Bayes Methods with A Selection of Fast Correlation Based Filter Features in Detecting Parkinson's Disease
on
LONTAR KOMPUTER VOL. 14, NO. 2 AUGUST 2023
DOI : 10.24843/LKJITI.2023.v14.i02.p02
Accredited Sinta 2 by RISTEKDIKTI Decree No. 158/E/KPT/2021
p-ISSN 2088-1541
e-ISSN 2541-5832
Comparing Support Vector Machine and Naïve Bayes Methods with A Selection of Fast Correlation Based Filter Features in Detecting Parkinson's Disease
Yuniar Faridaa1, Nurissaidah Ulinnuhaa2, Hanimatim Mu’jizaha3, Latifatun Nadya Desinainia4, Silvia Kartika Saria5
aDepartment of Mathematics, Faculty of Sains and Technology, UIN Sunan Ampel Surabaya, Jl. Ahmad Yani 117, Surabaya, Indonesia 50275 1yuniar_farida@uinsby.ac.id (corresponding author) 2nuris.ulinnuha@uinsby.ac.id
3hanimmujizah@gmail.com 4nadya.desinaini@gmail.com 5silviakartikas08@gmail.com
Abstract
Dopamine levels fall due to brain nerve cell destruction, producing Parkinson's symptoms. Humans with this illness experience central nervous system damage, which lowers the quality of life. This disease is not deadly, but when people's quality of life decreases, they cannot perform daily activities as people do. Even in one case, this disease can cause death indirectly. Contrast support vector machines (SVM) and naive Bayesian approaches with and without fast correlationbased filter (FCBF) feature selection, this study attempts to determine the optimum model to detect Parkinson's disease categorization. In this study, datasets from the UCI Machine Learning Repository are used. The results showed that SVM with FCBF achieved the highest accuracy among all the models tested. SVM with FCBF provides an accuracy of 86.1538%, sensitivity of 93.8775%, and specificity of 62.5000%. Both methods, SVM and Naive Bayes, have improved in performance due to FCBF, with SVM showing a more significant increase in accuracy. This research contributed to helping paramedics determine if a patient has Parkinson's disease or not using characteristics obtained from data, such as movement, sound, or other pertinent factors.
Keywords: Parkinson's disease, Fast Correlation-Based Filter, Support Vector Machine, Naïve Bayes
Parkinson's disease still affects people, and its prevalence must not be understated. According to data from the World Health Organization (WHO), in 2017, 25% of individuals globally were affected with Parkinson's disease [1]. Parkinson's is a cell-based degenerative disease in which the tissue mechanisms in Parkinson's division grow malignant. The growth is an aggressive neoplasm with abnormal increases in excessive amounts, so it is the cause of damage to cell tissue in Parkinson's [2]. The second most common neurological ailment, Parkinson's disease, affects 2-3% of adults over 65. Loss of nerve cells in the substantia nigra, which transmits impulses that control movement, is the outcome of the disorder, which affects the brain's most profound neurological system. Reduced sense of smell, constipation, sleeplessness, limb tremors, and trouble moving are common symptoms among Parkinson's patients [3]. Parkinson's can be detected using voice recording. Patients were asked to pronounce vowels with a class 1 sound level measuring microphone 8 cm in front of the lips. The amplitude of the resulting signal will be digitally normalized to determine the difference in the patient's behavior. Multidimensional speech program (MDVP) increase was used to assess many aspects of sound variation, including harmonic-to-noise ratio (HNR), harmonic-to-harmonic ratio (NHR), amplitude (simmer), and period (jitter). Other parameters are also calculated to describe the degree of complexity of sound recordings' signals and fractal dimensions [4].
Previous studies have identified several risk factors for this illness. In males, the age range of 40 to 70 is higher for this condition [5]. Parkinson's patients had anxiety and hopelessness rates of 25.81 percent and 11.17 percent, respectively. In Cui et al.'s research [6], several risk variables that impact the quality of life for individuals with Parkinson's disease were found. Anxiety, dyskinesias, poor sleep, and increased motor function are risk factors for depression in Parkinson's disease patients. More severe autonomic dysfunction is a risk factor for PD patients with compression, but rapid eye movement behavior (RBD) is not.
Further studies by Mazon et al. [7], concentrating on Alzheimer's and Parkinson's, demonstrated the connection between metabolic alterations and neurodegenerative illnesses. He discussed the relationship between obesity and the onset of neurodegenerative diseases, such as Alzheimer's and Parkinson's. It has been shown that obesity significantly affects how Parkinson's and Alzheimer's disease progress. Obesity-induced metabolic alterations in the central nervous system (CNS) may cause apoptosis and cell necrosis, which can ultimately result in neuronal death. These alterations also impact the synaptic plasticity of neurons.
Monocyte chemoattractant protein-1 and APQ3-IR have been linked to Parkinson's disease in Indonesia, as have age, minimum pitch, maximum pitch, average pitch, jitter level, adiponectin, glucose, and shimmer. Information gathered about Parkinson's illness at the University Hospital of Coimbra supports this. This data considers age, minimum vocal basal, maximum vocal basal, average vocal basal, jitter, simmer (dB), glucose, and simmer: APQ3-IR and monocyte chemoattractant protein-1. Early detection efforts are being made to reduce the impact of Parkinson's. This effort can be made using classification methods. Support Vector Machines (SVM) and Nave Bayes (NB) are widely used classification methods in previous research. The SVM approach faces challenges in the pattern (curse of dimensionality), is efficient to apply, and can generalize patterns that do not fit into the class. The SVM model has distinct advantages for handling small samples of nonlinear and high-dimensional issues. It is less prone than the ANN model to become caught in locally optimal solutions. As a result, data classification, pattern recognition, regression analysis, and other processes frequently use the SVM model [8]. The NB technique, in comparison, has the benefits of quick calculation times, high accuracy, and straightforward algorithms. The NB algorithm benefits from simple logic and consistent performance because it operates under the assumption that all features are independent. Although it is frequently challenging to meet the independence criteria, the NB classifier performs well in practical applications [9].
SVM and NB are frequently employed in studies, as demonstrated by Roy et al. [10], who used NB classifiers, SVM-boosted trees, and random forests to separate early Parkinson's disease patients from the general population and perform early (or preclinical) diagnosis of Parkinson's disease. The results show that the SVM classifier performs best (accuracy 96.40%, sensitivity 97.03%, specificity 95.01%, area under ROC 98.88%). Combining non-motor, CSF, and imaging indices can support the preclinical diagnosis of Parkinson's disease.
Emon et al. [11] carried out a different investigation with Naive Bayes. They used various data mining techniques, including naive Bayes, K-nearest, and Random Forest classifiers, to diagnose hepatitis. The inquiry yielded the following results: K-nearest neighbors had a 95.8 percent accuracy rate with 10-fold cross-validation, Random Forest had a 98.6 percent accuracy rate, and Naive Bayes had a 93.2 percent accuracy rate. Bashar et al. [12] coupled Simulated Annealing (SA) and SVM to determine the elements influencing water consumption. The findings indicated that the SVM-SA's standard error was 0.578. The hybrid SVM-SA model performed better than other models.
Feature selection helps reduce irrelevant features so that the performance of classification algorithms can be improved. One of these methods used is the Fast-Based Correlation Filter (FCBF). This FCBF method can provide exemplary performance in time and accuracy on classification algorithms. Li et al. [13] identified WT-FCBF-LSTM (wavelet transform, fast correlation-based filter, and long short-term memory) was introduced as part of the combined model. The findings indicate that compared to his LSTM, WT-LSTM, and FCBF-LSTM models, the WT-FCBF-LSTM model has a greater prediction accuracy. The MRE and RMSE of the single express and split services forecasts are lower than the combined express and split services forecasts. This suggests that WT-FCBF-LSTM can effectively capture various geographic and temporal aspects of express and side-split services to improve prediction accuracy. Djellali et al.
[14] identified WDBC (Wisconsin State Diagnosed Breast Cancer), colon, hepatitis, diffuse large B-cell lymphoma (DLBCL), and lung cancer datasets were classified using feature selection methods using FCBF and particle swarm optimization (PSO). The study's findings demonstrate that the FCBF-PSO approach performs more accurately than the FCBF-GA technique, with the former with an accuracy value of 86.11% and the latter with an accuracy value of 83.33% for PSO without FCBF.
Parkinson's disease stands out uniquely for its distinct suite of biomedical sound measurements used to diagnose and differentiate it from other conditions. This sound measurement includes parameters such as average vocal fundamental frequency, fundamental frequency variation, amplitude variation, and more. This compilation of specific biomedical sound measurements differentiates Parkinson's disease from other conditions. FCBF is specifically used to identify the most relevant and discriminatory features for classification purposes. Finding the most critical characteristics to use in successfully separating people with Parkinson's disease from those who do not has been made easier using FCBF.
Our research explores the early detection of Parkinson's disease by comparing the Support Vector Machines (SVM) and Naïve Bayes (NB) methods. Although SVM and NB are robust, the complexity of Parkinson's disease necessitates a practical approach due to its complex features. We integrate a Fast Correlation-Based Filter (FCBF) for feature selection. Our study focuses on implementing the FCBF method in the context of Parkinson's disease detection. By comparing the performance of SVM and NB with and without FCBF, we aim to explain the effectiveness of these methods. This dataset has previously been the object of research by Avci to diagnose Parkinson's disease using the Kernel Extreme Learning Machine Genetic-Wavelet Algorithm [15].
This study uses two methods, SVM and Naïve Bayes, that will be compared to find the best model to detect Parkinson's disease classification with FCBF feature selection and without feature selection.
FCBF was developed by Yu and Liu [16] to perform feature selection. This algorithm has the principle that features related to classes but not excessive to other connecting features are good features, so two random variables can be measured in correlation using symmetrical uncertainty (SU), which is between 0 and 1. Equation 1 shows the SU equation [14], [17].
SU(X1V) = 2 ×
■ IG(X∣Y)
.H(X)+H(Y)
[
■]
(1)
H(X) is the entropy value of X, and H(X∣Y) is the entropy value of X if the Y variable is known with IG(X∣Y) as the information gain.
SVM is a classification technique for predicting classes using machine-learning training [18]. The training process is performed with input data known to be labeled to create the model. The result of the pattern-shaped method is a dividing line of two classes, namely the +1 and -1 classes, called hyperplanes. Hyperplane optimization can be determined by measuring the distance between the hyperplane and the closest pattern within each category. This method's equation can be presented in Equation 2 [19], [20].
f(x) = w(x) + b
(2)
Where w is the weight, x is the input variable (data), and b is the bias. Edge values should be maximized to get the best hyperplane values. Figure 1 shows an ideal hyperplane image.
Figure 1. SVM with hyperplane separating two classes [21]
The NB algorithm uses an independent feature model, where in the same data, the features stand alone and have nothing to do with other components [22]. NB classifiers are based on Bayes' theorem, which states that each part contributes to the target class independently and equally. Bayes' theorem is the basic rule of the Naive Bayes classifier. Equation 3 will give the Bayes theorem [23], [24], [25].
P(H∖E) =
P(E∖H) × P(H) P(E)
(3)
P(H) is the likelihood that the initial (prior) hypothesis H occurs without seeing any evidence. In contrast, P(H∖E) is a hypothesis H occurring if there is evidence that E occurs. The likelihood that evidence E will impact hypothesis H is P(E∖H). And P(E) is the likelihood, absent consideration of additional assumptions or evidence, that the original (prior) evidence E will occur [26], [25]. As per Bayes' rule [25], the initial probability (P(H)) represents the possibility of a hypothesis before the observation of evidence. In contrast, the final probability H, P(H∖E) represents the likelihood of an idea after the preservation of proof. This strategy also offers certain benefits and drawbacks based on the idea. The advantage of this Bayes theorem is that the amount of training data needed is small, can be used by quantitative and discrete data, can function well on various types of data, and can solve not only a single proof but also more than one other. For instance, if you are familiar with the multiple proofs E1, E2, and E3, you may write the final probability of Bayes' theorem using equation 4 [10], [25]:
P(H∖E1,E2,E3)
P(E1,E2,E3∖H)×P(H)
P(E1,E2,E3)
(4)
The advantages and disadvantages of the Bayes theorem are that it can only be used in statistical data, can't apply if the conditional probability is zero, and there must be early learning to determine decisions [10].
The data in the input feature is transformed into features space using the kernel trick in the SVM learning model procedure. The kernel can translate data into kernel space, a higher-dimensional space, where this process can separate the data linearly [27]. Several kernels are used in SVM: linear, polynomial, RBF, and sigmoid.
Each element of the Hessian matrix represents the second partial derivative of the function. The Hessian matrix f(x), an n-variable function with a second partial derivative and a continuous derivative, can be represented in equation 6 [31].
|
H = |
' d f dx1 d2f dx2dι |
d2f dx1d2 d2f dx2 |
. d2f dxιdn d2f dx2dn |
(5) |
|
.d2f. |
d2f |
d: | ||
|
.dXγιd1 |
dxnd2 |
dxn. |
This Hessian matrix evaluates the derivatives of two functions of more than one variable. More precisely, it is used to identify the static point function of two or more variables. For example, f(x) = f(x1,............,xn) is a real-valued function whose second partial derivatives are all
continuous [32].
A confusion matrix is an approach to understanding information that contains actual data and predictions based on classification findings. It is anticipated in classification to categorize data precisely and generate good results with few mistakes. As a result, this approach exists to help determine how effective categorization is [33]. The Confusion matrix produces the following primary results: accuracy, precision, specificity, and sensitivity. Table 1 displays the confusion matrix table. Before determining the preliminary results, each of the parameters in Table 1 must be recognized [19], [33], [34].
Table 1. Table of Confusion Matrix
|
Actual or Classification |
Positive |
Negative |
|
Positive |
TP or True Positive |
FN or False Negative |
|
Negative |
FP or False Positive |
TN or True Negative |
Equations 5, 6, and 7 were used to calculate the accuracy, sensitivity, and specificity after obtaining each of the characteristics listed in Table 1.
TP + TN Accuracy = —————-—— TP + TN + FP + FN
(6)
(7)
(8)
TP
Sensitivity = ——— y TP+ FN
TN
Specificity = ———— TN + FP
The UCI Machine Learning Repository provides access to numeric data from the Parkinson's Disease dataset created by Max Little at the University of Oxford in collaboration with the Colorado National Center for Speech and Language. There are as many as 22 parameters of speech signal recording lab results, with the number of people with Parkinson's as many as 147 people and normal people as many as 48 [35]. This data will be split into training and testing, with an 80:20 ratio. There are 156 training and 39 test data, including data from 29 Parkinson's patients and ten normal subjects. After data release, feature selection and classification procedures are used.
To assess the effectiveness of a model or algorithm, the initial step in this study was to divide the data into training and testing sections using k-fold cross-validation, a statistical approach. The data is split into equal (or nearly equal) k-folds for k-fold cross-validation. In each subsequent round of training and testing, a specific data fold is used for testing, and the remaining k-1 folds are used for activity [36],[37]. We employed k-fold cross-validation with a k value of 5 in this study.
The next stage is the feature selection process. This process reduces features that are not required to simplify the classification process. The selection of parts used is the FCBF method. Good accuracy is obtained from the threshold parameters entered into the FCBF. The FCBF data results fall into two categories: training data and test data. The data is also transferred to the classification phase using the SVM and NB methods.
The SVM method's first step is to input data on Parkinson's disease. After obtaining the data, the SVM kernel is calculated as the next step. The following computation process finds the Hessian matrix's importance and runs the sequential SVM training and SVM test processes' computation processes. The final step in the SVM process is to evaluate its classification.
The NB method first computes the probability of each label, and the case probability of each brand determines the possibilities of problematic labels (data test) and compares the probability results of each title. In addition, this study also classified Parkinson's disease data without the process of selecting features that will be compared to the level of accuracy. Based on these measures, the results of this method comparison are expected to obtain the best model for diagnosing Parkinson's disease.
This study's output is the classifier's accuracy, which gauges how well the recognition process worked. The likelihood of the card succeeding increases with precision. Feature selection and classification are used in both stages of the identification process.
Feature selection aims to reduce redundant functionality and retain related components. The choice of features in this study uses FCBF with a threshold of 0.7, whose results will be used at the classification stage. A comparison of the parameter results with and without FCBF is shown in Table 2. From the table, we can see that there are 22 parameters and ten parameters after selecting the characteristic.
|
Table 2. Comparison of parameters using FCBF and without FCBF | ||
|
No. |
Abbreviation |
Feature description |
|
1 |
MDVP: FO (Hz) |
Average vocal fundamental frequency |
|
2 |
MDVP: Fhi (Hz) |
Maximum vocal fundamental frequency |
|
3 |
MDVP: Flo (Hz) |
Minimum vocal fundamental frequency |
|
4 |
MDVP: Jitter (%) |
MDVPjitter in percentage |
|
5 |
MDVPiJitter(Abs) |
MDVP absolute jitter in ms |
|
6 |
MDVP: RAP |
MDVP relative amplitude perturbation |
|
7 |
MDVP: PPQ |
MDVP five-point period perturbation quotient |
|
8 |
Jitter: DDP |
Average absolute difference Ofdifferences between jitter cycles |
|
9 |
MDVP: Shimmer |
MDVP local shimmer |
|
10 |
MDVP: Shimmer (dB) |
MDVP local shimmer in dB |
|
11 |
Shimmer: APQ3 |
Three-Pointamplitude perturbation quotient |
|
12 |
Shimmer: APQ5 |
Five-point amplitude perturbation quotient |
|
13 |
MDVP: APQ11 |
MDVP 11-point amplitude perturbation quotient |
|
14 |
Shimmer: DDA |
Average absolute differences between the |
|
amplitudes of consecutive periods | ||
|
15 |
NHR |
Noise-to-harmonics ratio |
|
16 |
HNR |
Harmonics-to-noise ratio |
|
17 |
RPDE |
Recurrence period density entropy measure |
|
18 |
D2 |
Correlation dimension |
|
19 |
DFA |
Signal fractal scaling exponent of detrended |
|
fluctuation analysis | ||
|
20 |
Spread 1 |
Two nonlinear measures Offundamental |
|
21 |
Spread2 |
Frequency variation |
|
22 |
PPE |
Pitch period entropy |
* The colored bar is the selected feature by FCBF
Feature selection data fall into two classes. Class 0 indicates no Parkinson's disease, and class 1 exhibits symptoms. The data classification process is performed using SVM and NB methods. The initial SVM used is a linear kernel type. The results of accuracy testing by selecting FCBF features of 2 to 11 features for the SVM-Linear Kernel and Naive Bayes (NB) classifier are presented in Table 3. It can be observed that the accuracy of the SVM classifier varies for several different features, ranging from 84.6154% to 86.1538%. Likewise, the Naive Bayes classifier shows accuracy ranging from 74.8718% to 80.5128% as the number of features selected changes. It was found that the best accuracy of the two models, both SVM and Naive Bayes, occurs when the number of features is specified as two, with SVM accuracy reaching 86.1538% and NB accuracy of 80.5128%. The two features used in the classification model are spread1 and PEP.
|
Table 3. The results of the accuracy of the test are based on the number of features with FCBF | ||
|
Number of features |
SVM Linear-FCBF |
NB-FCBF |
|
2 |
86.1538% |
80.5128% |
|
3 |
85.6410% |
77.9487% |
|
4 |
84.6154% |
78.9744% |
|
5 |
85.1282% |
77.4359% |
|
6 |
85.1282% |
78.4615% |
|
7 |
85.1282% |
80.0000% |
|
8 |
85.1282% |
77.9487% |
|
9 |
85.1282% |
76.9231% |
|
10 |
84.6154% |
74.8718% |
|
11 |
84.6154% |
74.8718% |
The next step is to test the SVM kernel type to find the kernel with the best performance. Table 4 shows the SVM-FCBF performance test results based on the kernel type. Among these kernels, the linear kernel achieved the highest accuracy of 86.1538%, followed by the polynomial and RBF kernels, which achieved an accuracy of 85.1282% each. However, the Sigmoid kernel has the lowest accuracy of 50.7692%.
Table 4. SVM-FCBF performance test results based on kernel type Kernel
|
Parameter |
Linear |
Polynomial |
RBF |
Sigmoid |
|
Accuracy |
86.1538% |
85.1282% |
85.1282% |
50.7692% |
|
Sensitivity |
93.8776% |
93.1973% |
95.2381% |
67.3469% |
|
Specificity |
62.5000% |
60.4167% |
54.1667% |
0.0000% |
Table 5. Results of accuracy, sensitivity, and specificity testing with and without FCBF are compared
|
Parameters |
SVM |
SVM-FCBF |
NB |
NB-FCBF |
|
Accuracy |
85,6410% |
86.1538% |
70.7692% |
80.5128% |
|
Sensitivity |
95.2380% |
93.8775% |
63.9455% |
81.6327% |
|
Specificity |
56.2500% |
62.5000% |
91.6667% |
78.9116% |
Table 5 compares the accuracy, sensitivity, and specificity results with and without FCBF for the SVM and NB methods. SVM with FCBF achieves the highest accuracy among all models. This suggests that when combined with FCBF feature selection, SVM balances correctly identifying positive cases and overall accuracy. Table 4 also shows that the SVM-FCBF increased the specificity by 6.25%, but the sensitivity decreased by 1.4%. Despite this, the sensitivity value
remains high above 90%. The high sensitivity indicates that the model effectively reduces false negatives, ensuring actual disease cases are not missed at diagnosis. If sensitivity is low, the model may misclassify individuals with Parkinson's as healthy, resulting in false negative results. This can delay or prevent early diagnosis and intervention. Meanwhile, NB without FCBF had the highest specificity, indicating that it is better at correctly identifying negative cases, but the sensitivity is lower. The results highlight the importance of feature selection (FCBF) in improving model performance. Both SVM and NB benefit from FCBF and SVM shows more significant accuracy improvements.
The running time results, both with and without the application of FCBF feature selection, are presented in Table 6. The running time for the SVM classifier shows a significant decrease when FCBF feature selection is used, mainly when the number of features selected is limited to only two. For the SVM classifier, the running time was significantly reduced from 3.4942 seconds without FCBF to 0.0529 seconds with FCBF. This reduction in running time can be attributed to a simplified computational process due to reduced feature dimensions achieved through FCBF.
However, the reduction in running time did not occur in the NB classifier. When FCBF feature selection is implemented, the running time for the NB classifier increases slightly from 0.0255 seconds without FCBF to 0.0383 seconds with FCBF. This may be because the computational efficiency of the NB algorithm is inherently less affected by reduced feature dimensions compared to SVM. On the other hand, the NB model gives the lowest results. Although FCBF aims to maintain relevant features, this may not align with the feature independence assumption in Naive Bayes. Therefore, the lower performance of Naive Bayes can be attributed to the model's inability to capture complex inter-feature relationships.
Table 6. Results of running time with and without FCBF are compared
Parameters SVM SVM-FCBF NB NB-FCBF
Running time (s) 3.4942 0.0529 0.0255 0.0383
The results can be illustrated with the Characteristic Operating Receiver (ROC) graph. Figure 2 displays a Roc graphic image using the SVM-FCBF technique.
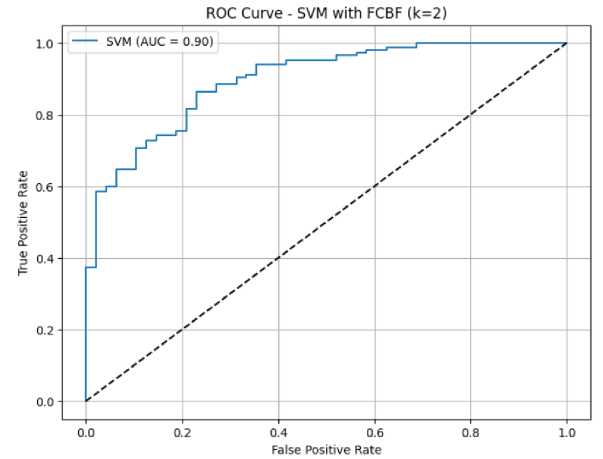
Figure 2. ROC graphics of SVM-FCBF methods
The ROC chart describes the results of the confusion matrix, with horizontal lines being false positive and vertical being genuinely positive. The Area Under Curve (AUC) value obtained from this chart is 0.9, with a reasonable accuracy value. Table 4 displays the SVM-FCBF method's confusion matrix table.
Table 4. Confusion matrix method SVM-FCBF
Actual / Classification Positive Negative
Positive 30 18
Negative 9 138
This dataset has previously been the object of research by Avci to diagnose Parkinson's disease using the Kernel Extreme Learning Machine Genetic-Wavelet Algorithm [15]. The study achieved the highest accuracy rate of 96.81%, where the accuracy score was much higher than the accuracy of this research model (SVM-FCBF), which reached 86.1538%. This may help clarify the possible avenues for future model performance improvements and the enhancements that can be made in this area.
A system that implements the SVM and NB methods and identifies Parkinson's disease through a feature selection process using a fast correlation-based filter is a system that can perform accurate classification. The feature selection process successfully identifies relevant features that are later used in the identification process. The other step is classification preparation utilizing the SVM and NB strategies. Based on the results obtained, SVM-FCBF is the best result. The SVM-FCBF classification has an accuracy of 86.1538%, a sensitivity of 93.8775%, and a specificity of 62.5000%. As future studies intend to apply SVM and Naive Bayes to detect Parkinson's disease, these results could be used as a reference. The outcomes of this study can also be tested using a widely utilized method, namely the Deep Learning approach, which may obtain better research results.
References
-
[1] WHO, Atlas - Country resources for neurological disorders, vol. 30, no. November. 2017. [Online]. Available: https://www.who.int/publications/i/item/atlas-country-resources-for-
neurological-disorders
-
[2] A. Elbaz, L. Carcaillon, S. Kab, and F. Moisan, "EPIDEMIOLOGY OF PARKINSON' S DISEASE The Rotterdam Study," Reveu Neurologique (Paris)., vol. 172, no. 1, pp. 14–26, 2016, doi: 10.1016/j.neurol.2015.09.012.
-
[3] R. Pahwa and K. E. Lyons, Handbook of Parkinson's Disease, Fifth Edit. 2013.
-
[4] Y. Wu et al., "Dysphonic Voice Pattern Analysis of Patients in Parkinson's Disease Using Minimum Interclass Probability Risk Feature Selection and Bagging Ensemble Learning Methods," Computational and Mathematical Methods in Medicine, vol. 2017, 2017, doi: 10.1155/2017/4201984.
-
[5] E. Muliawan, S. Jehosua, and R. Tumewah, “Diagnosis dan Terapi Deep Brain Stimulation pada Penyakit Parkinson,” Jurnal Neurologi Manado SINAPSIS, vol. 1, no. 1, pp. 67–84, 2018.
-
[6] S. S. Cui et al., "Prevalence and risk factors for depression and anxiety in Chinese patients with Parkinson's disease," BMC Geriatrics, vol. 17, no. 1, pp. 1–10, 2017, doi:
10.1186/s12877-017-0666-2.
-
[7] J. N. Mazon, A. H. de Mello, G. K. Ferreira, and G. T. Rezin, "The impact of obesity on neurodegenerative diseases," Life Sciences, vol. 182, pp. 22–28, 2017, doi:
10.1016/j.lfs.2017.06.002.
-
[8] J. Li, Y. Lei, and S. Yang, "Mid-long term load forecasting model based on support vector machine optimized by improved sparrow search algorithm," Energy Reports, vol. 8, pp. 491– 497, 2022, doi: 10.1016/j.egyr.2022.02.188.
-
[9] G. Yang and X. Gu, "Fault Diagnosis of Complex Chemical Processes Based on Enhanced Naive Bayesian Method," IEEE Transactions on Instrumentation and Measurement, vol. 69, no. 7, pp. 4649–4658, 2020, doi: 10.1109/TIM.2019.2954151.
-
[10] R. Prashanth, S. Dutta Roy, P. K. Mandal, and S. Ghosh, "High-Accuracy Detection of Early Parkinson's Disease through Multimodal Features and Machine Learning," International Journal of Medical Informatics, vol. 90, pp. 13–21, 2016, doi: 10.1016/j.ijmedinf.2016.03.001.
-
[11] T. I. Trishna, S. U. Emon, R. R. Ema, G. I. H. Sajal, S. Kundu, and T. Islam, "Detection of
Hepatitis (A, B, C, and E) Viruses Based on Random Forest, K-nearest and Naïve Bayes Classifier," 2019 10th International Conference on Computing, Communication and Networking Technologies (ICCCNT), pp. 1–7, 2019, doi:
10.1109/ICCCNT45670.2019.8944455.
-
[12] A. M. Bashar, H. Nozari, S. Marofi, M. Mohamadi, and A. Ahadiiman, "Investigation of factors affecting rural drinking water consumption using intelligent hybrid models," Water Science and Engineering., vol. 16, no. 2, pp. 175–183, 2022, doi: 10.1016/j.wse.2022.12.002.
-
[13] X. Li, Y. Zhang, M. Du, and J. Yang, "The forecasting of passenger demand under hybrid ridesharing service modes: A combined model based on WT-FCBF-LSTM," Sustainable Cities and Society., vol. 62, no. April, p. 102419, 2020, doi: 10.1016/j.scs.2020.102419.
-
[14] H. Djellali and S. Guessoum, "Fast Correlation based Filter combined with Genetic Algorithm and Particle Swarm on Feature Selection Hayet," 2017 5th International Conference on Electrical Engineering - Boumerdes (ICEE-B), vol. 2017-Janua, pp. 1–6, 2017.
-
[15] D. Avci and A. Dogantekin, "An Expert Diagnosis System for Parkinson's Disease Based on Genetic Algorithm-Wavelet Kernel-Extreme Learning Machine," Parkinson's Disease, vol. 2016, 2016, doi: 10.1155/2016/5264743.
-
[16] L. Yu and H. Liu, "Feature Selection for High-Dimensional Data: A Fast Correlation-Based Filter Solution," ICML'03: Proceedings of the Twentieth International Conference on International Conference on Machine Learning, vol. 2, pp. 856–863, 2003.
-
[17] Y. Zhang, G. Pan, Y. Zhao, Q. Li, and F. Wang, "Short-term wind speed interval prediction based on artificial intelligence methods and error probability distribution," Energy Conversion and Management. Manag., vol. 224, no. August, p. 113346, 2020, doi:
10.1016/j.enconman.2020.113346.
-
[18] D. N. Avianty, P. I. G. P. S. Wijaya, and F. Bimantoro, "The Comparison of SVM and ANN Classifier for COVID-19 Prediction," Lontar Komputer - Jurnal Ilmiah Teknologi Informasi, vol. 13, no. 2, p. 128, 2022, doi: 10.24843/lkjiti.2022.v13.i02.p06.
-
[19] A. Z. Foeady, D. C. R. Novitasari, A. H. Asyhar, and M. Firmansjah, "Automated Diagnosis System of Diabetic Retinopathy Using GLCM Method and SVM Classifier," 2018 5th International Conference on Electrical Engineering, Computer Science and Informatics (EECSI), pp. 154–160, 2019, doi: 10.1109/eecsi.2018.8752726.
-
[20] A. Manoharan, K. M. Begam, V. R. Aparow, and D. Sooriamoorthy, "Artificial Neural Networks, Gradient Boosting and Support Vector Machines for electric vehicle battery state estimation: A review," Journal of Energy Storage, vol. 55, no. PA, p. 105384, 2022, doi: 10.1016/j.est.2022.105384.
-
[21] A. Roy and S. Chakraborty, "Support vector machine in structural reliability analysis: A review," Reliability Engineering & System Safety, vol. 233, no. January, p. 109126, 2023, doi: 10.1016/j.ress.2023.109126.
-
[22] L. P. Wanti, N. W. A. Prasetya, L. Sari, L. Puspitasari, and A. Romadloni, "Comparison of Naive Bayes Method and Certainty Factor for Diagnosis of Preeclampsia," Lontar Komputer - Jurnal Ilmiah Teknologi Informasi, vol. 13, no. 2, p. 105, 2022, doi:
10.24843/lkjiti.2022.v13.i02.p04.
-
[23] Z. Deng, T. Han, Z. Cheng, J. Jiang, and F. Duan, "Fault detection of petrochemical process based on space-time compressed matrix and Naive Bayes," Process Safety and Environmental Protection, vol. 160, pp. 327–340, 2022, doi: 10.1016/j.psep.2022.01.048.
-
[24] Q. Tan et al., "A new sensor fault diagnosis method for gas leakage monitoring based on the naive Bayes and probabilistic neural network classifier," Measurement, vol. 194, no. 6, March, p. 111037, 2022, doi: 10.1016/j.measurement.2022.111037.
-
[25] Y. Farida and N. Ulinnuha, “Klasifikasi Mahasiswa Penerima Program Beasiswa Bidik Misi Menggunakan Naive Bayes,” Systemic Information System and Informatics Journal, vol. 4, no. 1, pp. 17–22, 2018, doi: 10.29080/systemic.v4i1.317.
-
[26] B. Rajoub, Supervised and unsupervised learning. Elsevier Inc., 2020. doi: 10.1016/b978-0-12-818946-7.00003-2.
-
[27] A. Roy, R. Manna, and S. Chakraborty, "Support vector regression based metamodeling for structural reliability analysis," Probabilistic Engineering Mechanics, vol. 55, no. September 2018, pp. 78–89, 2019, doi: 10.1016/j.probengmech.2018.11.001.
-
[28] X. Lin, L. Zhao, C. Shang, W. He, W. Du, and F. Qian, "Data-driven robust optimization for cyclic scheduling of ethylene cracking furnace system under uncertainty based on kernel learning," Chemical Engineering Science, vol. 260, p. 117919, 2022, doi:
10.1016/j.ces.2022.117919.
-
[29] D. Wilk-Kolodziejczyk, K. Regulski, and G. Gumienny, "Comparative analysis of the properties of the nodular cast iron with carbides and the austempered ductile iron with use of the machine learning and the support vector machine," The International Journal of Advanced Manufacturing Technology, vol. 87, no. 1–4, pp. 1077–1093, 2016, doi:
10.1007/s00170-016-8510-y.
-
[30] Z. Zhao et al., "Multi support vector models to estimate solubility of Busulfan drug in supercritical carbon dioxide," Journal of Molecular Liquids, vol. 350, p. 118573, 2022, doi: 10.1016/j.molliq.2022.118573.
-
[31] W. Dong, S. Gao, and S. S. T. Yau, "Hessian matrix non-decomposition theorem and its application to nonlinear filtering," Nonlinear Analysis, vol. 230, p. 113236, 2023, doi: 10.1016/j.na.2023.113236.
-
[32] M. Xu and C. Shi, "A Hessian recovery-based finite difference method for biharmonic problems," Applied Mathematics Letters, vol. 137, no. 12271482, p. 108503, 2023, doi: 10.1016/j.aml.2022.108503.
-
[33] Y. Wang, Y. Jia, Y. Tian, and J. Xiao, "Deep reinforcement learning with the confusionmatrix-based dynamic reward function for customer credit scoring," Expert Systems with Applications, vol. 200, no. March, p. 117013, 2022, doi: 10.1016/j.eswa.2022.117013.
-
[34] D. C. R. Novitasari, A. H. Asyhar, M. Thohir, A. Z. Arifin, H. Mu'jizah, and A. Z. Foeady, "Cervical Cancer Identification Based Texture Analysis Using GLCM-KELM on Colposcopy Data," 2020 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), pp. 409–414, 2020, doi: 10.1109/ICAIIC48513.2020.9065252.
-
[35] Oxford, "Parkinson's Data Set," UCI Learning Repository, 2007.
https://archive.ics.uci.edu/ml/datasets/parkinsons (accessed Mar. 05, 2020).
-
[36] Y. Jung, "Multiple predicting K-fold cross-validation for model selection," Journal of Nonparametric Statistics, vol. 30, no. 1, pp. 197–215, 2018, doi:
10.1080/10485252.2017.1404598.
-
[37] P. Refaeilzadeh, L. Tang, H. Liu, L. Angeles, and C. D. Scientist, "Encyclopedia of Database Systems," Encyclopedia of Database Systems, 2020, doi: 10.1007/978-1-4899-7993-3.
90
Discussion and feedback