Dynamic Neural Network Model Design for Solar Radiation Forecast

LONTAR KOMPUTER VOL. 13, NO. 2 AUGUST 2022

DOI : 10.24843/LKJITI.2022.v13.i02.p03

Accredited Sinta 2 by RISTEKDIKTI Decree No. 158/E/KPT/2021

p-ISSN 2088-1541

e-ISSN 2541-5832

Dynamic Neural Network Model Design for Solar Radiation Forecast

Syamsul Bahri^a1, Muhammad Rijal Alfian^a, and Nurul Fitriyani^a

^a Department of Mathematics, Faculty of Mathematics and Sciences, University of Mataram Mataram, Indonesia

¹syamsul.math@unram.ac.id (corresponding author)

Abstract

Sunlight is an energy source that is a gift from God and is a source of life for living things, including humans as caliphs on earth. Judging from its impact, solar radiation is an environmental parameter that has positive and negative effects on human life. The pattern of distribution of solar radiation is important information for human life to be the attention of many people, both policymakers and researchers in the field of environment. This study objects to modeling the radiation of solar using a dynamic neural network (DNN) model. The data used in this research is the meteorological data of Mataram City for the period January 2018 to May 2019, which was obtained from the Department of Environment and Forestry of West Nusa Tenggara Province. In the development of this model, solar radiation was seen as a function of a combination of several variables related to meteorological (wind speed, wind direction, humidity, air pressure, and air temperature) and solar radiation data at some previous time. Considering the advantages and effectiveness of the activation function in the proposed DNN model learning process, this study's network learning in the hidden layer employed two activation functions: hyperbolic tangent (Type I) and hyperbolic tangent sigmoid functions (Type II). The output aggregation used two aggregates for each type: the weighted aggregation function (Type a) and the maximum function (Type b). The results of computer simulations based on the root of mean square error (RMSE) measure indicate that the model for modeling solar radiation in these two cases is quite accurate. Furthermore, it could be seen that the model's performance using the hyperbolic tangent activation function (Type b) is relatively better than the hyperbolic tangent sigmoid type of the activation function (Type a), with the RMSE values are 18.3924 and 18.4005, respectively.

Keywords: Design of Model, Sunlight, Solar Radiation, Meteorology, Dynamic Neural Network

• 1.    Introduction

The last two years have been stressful times for human life on earth. The world community is busy with the appearance of the Covid-19 pandemic (Coronavirus diseases 2019), including Indonesia. Secondary problems related to the Covid-19 pandemic have also appealed to the concern of many sides: the government as regulators and scientists as researchers. Those issues include the model for the spread of the virus, strategies for preventing the development of the virus and the location of its spread, providing vaccines and the vaccination process, social, economic, educational, and social impact, so as culture and the problems that follow.

Humans have made various efforts to maintain and improve health and immunity, such as consuming various vitamins that can increase endurance and, at certain times, basking in the sun. According to [1], immunity is an important factor for survival and preventing diseases caused by infections, including Covid-19 infection. Immunity is especially important for children since the process of bone formation and increasing endurance needs vitamin D. When the skin is exposed to sunlight containing ultraviolet (UV) rays, this process will trigger the synthesis of vitamin D in the body. Furthermore, the kidneys and liver convert it into active vitamin D, which can be used by the body to improve calcium absorption and bone health. Someone who gets sun exposure of sufficient duration will be one of the causes of meeting the need for vitamin D, which impacts the immune system. A good immune system will maintain a healthy body, including fighting the coronavirus. On the other hand, if the human body is exposed to excessive sunlight, it will have negative effects such as sunburn, triggering signs of skin aging (skin loosening and stretching),

and skin becoming rougher and drier. Direct exposure to sunlight can also increase the risk of skin cancer, damage eyes and hair color [2].

Based on the benefits and negative impacts caused by solar radiation, information and knowledge about the characteristics of daily solar radiation is a problem that must be studied and resolved. Mathematical modeling is a tool that can be used to identify and model the distribution pattern of solar radiation intensity. In this case, several studies on solar radiation intensity modeling techniques have been carried out, including modeling using statistics [3] and estimation methods [4]. The modeling of solar radiation using air pressure parameters has been carried out by [5]. The modeling uses a multi-layer perceptron-based neural network method by [6] and the wavelet neural network method [7]. Modeling using the time series method with the fundamental of ARMA [8] and machine learning [9]. Modeling using a non-linear time series basis has been carried out by [10].

Theoretically, the neural network model consists of two types: the statistic neural network model (static neural network or SNN) and the dynamic neural network model (dynamic neural network, DNN). The DNN model is a neural network model focusing on parameter changes over time. Based on these characteristics in modeling real problems, the use of the DNN model is more rational than the SNN model. Several studies related to the application of the DNN model include prediction of weather data [11], prediction of Zika virus risk [12], detection of seismic data anomalies [13], prediction of temperature at tube surface [14], segmentation and gesture recognition [15], and prediction of radio signal loss [16].

This study applied a dynamic neural network model (DNN) to model solar radiation using meteorological variables, namely wind speed, wind direction, humidity, air pressure, and air temperature as predictors. Besides meteorological variables, predictor variables were also used dynamically data on solar radiation some time in advance. DNN in this study was applied through the development of a DNN network architecture that utilizes the advantages and effectiveness of two types of activation functions, namely hyperbolic tangent and hyperbolic tangent sigmoid functions in the learning process in the hidden layer. Furthermore, for each type of activation function, the output aggregation process was distinguished again using the weighted aggregate function and the maximum function.

• 2.    Research Methods

This study used a dynamic neural network (DNN) model to model solar radiation. The meteorological data in Mataram, Lombok, West Nusa Tenggara Province used were secondary, obtained from the Department of Environment and Forestry, West Nusa Tenggara Province, from January 2018 to May 2019. The meteorological data in question consisted of wind speed (x₁), wind direction (x₂) , humidity (x₃), air temperature (x₄ ), and pressure (x₅).

The study was carried out in four (4) main stages, namely:

• (i) . The development of the model was started by studying the characteristics of solar radiation, one of the parameters of air pollution, as a response variable to several meteorological/weather variables. Meteorological variables were wind speed, direction, humidity, air temperature, and pressure. At this stage, the instrument used was correlation analysis, namely cross-correlation analysis between meteorological and solar radiation response variables. Furthermore, the effect of solar radiation data on several periods before t time was used for auto-correlation analysis.

• (ii) . DNN architecture development, including:

• a.  Determining the number of inputs,

• b.  Determining the number of DNS layers,

• c.  Determining the number of neurons (data) per layer,

• d.  Developing the architectural model of the dynamic neural network model used in

this study.

• (iii) . Creating a computational program based on the DNN model in step ii.

• (iv) . Numerical simulation using solar radiation actual data and several meteorological parameters in Mataram, Lombok Island, West Nusa Tenggara.

• 3.    Implementation of the DNN Model for Solar Radiation Modeling and Discussion
  
  3.1.    Proposed DNN architecture

This study's proposed dynamic neural network (DNN) architecture is visualized below.

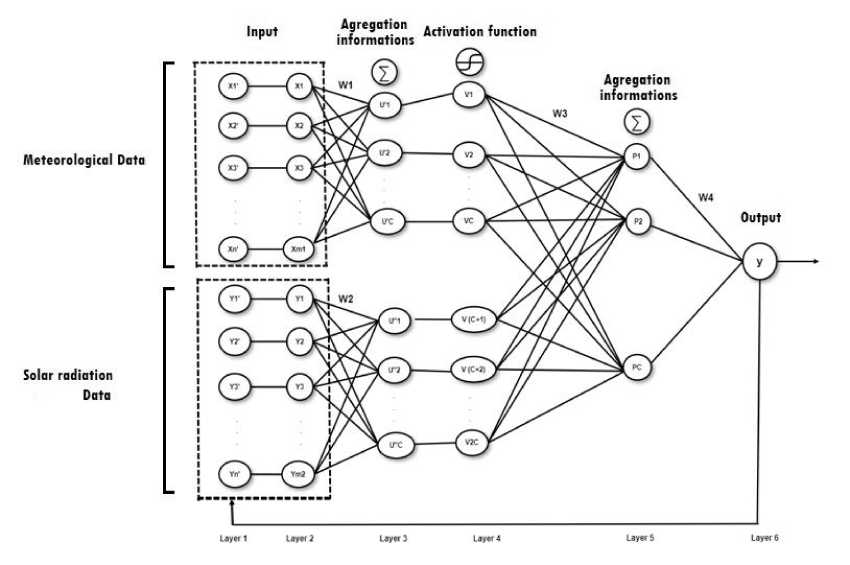
Figure 1. The proposed DNN architecture

• 3.2.    Process of feed-forward DNN

The feed-forward process on the DNN model proposed in this study can be described based on the following stages:

Layer 1: the input layer is divided into two input groups, namely the predictor input group in the form of the five meteorological variables mentioned, consisting of m1 data, and the input group data for solar radiation some time in advance consisting of m2 data.

Layer 2: the result of transforming the input data using the data normalization method with the following rules:

''

• X. = -√----min-

i''

maxmin

'''

X X and X respectively represent the i-th data, the minimum data, and the maximum data from the initial data row collection. In this layer, the number of neurons was the same as in layer 1, namely m = m₁ + m₂ neurons.

Layer 3: each data transformed in layer 2 was summed according to the weight of W1 for the first data group, and with the weight of W2_kj for the second data group, with i = 1,2,∙∙∙,m₁,

k = 1,2,∙∙∙,m₂ and j = 1,2,∙∙∙,C for a C which stated the number of classifications of the input data.

^m1

Uj=∑ W '.,Xj; j = 1∙2."∙. C dan U "=∑ W1 „X,' j = 1.2,-. C(2)

i=1

The number of neurons in this layer was 2C neurons.

Layer 4: The weighted data of U'_j and Uj for j = 1,2,∙∙∙,C was activated using two types of functions, namely hyperbolic tangent function (tanh) and hyperbolic tangent sigmoid function (tansig), as follows:

e^{2 Uj} -1

V^(U.) = tanh(^u) = -ip----, and                   (3a)

e ^j +1

1 - e "^2uj

V_j ^(uj) = ^{tan si}g^(u,) = ----—                 (3b)

• ^{j j                 j} 1 + e ¹

with U_j = U'_j or U_j = U'_j.

Layer 5: In this layer, the activation result of V_j., j = 1,2,∙∙∙,2Cwas summed again with the weights of W3_ip i = 1,2,-,2C and J = 1,2, ∙∙∙, C using the following equation:

• 2 C

• p, (v,) = ∑ W I_lVi, k = 1,2.-. C ■

j=1

Layer 6: The final output of the model is given by the equation:

C

Type a:                      y = α×∑W4p, + β, k = 1,2,∙∙∙,C(5)

k=1

C

Type b:                  y = α ×∑ max ( W 4 )× p_k + β, k = 1,2,∙∙∙, C(6)

k=1

for a real constant a and β.

• 3.3.    Optimization of learning parameters

Parameter optimization was carried out in the backward and forward steps of DNN. In this case, the optimized parameters included weight parameters of W1, W2, W3 , and W4. Parameter optimization using the gradient descent with momentum method to minimize the objective function:

i N             ²

E=N ∑( yj - yd)                       (7)

N represents the amount of data, while y y^d and respectively represents the output value of the proposed DNN model and the target data value.

The backward step optimization process was carried out using the following partial differential equations:

∂E _lE_ ∂y ∂p ∂V ∂ U U

lW1 ~ly lp lV IUf lW1               ⁽⁸⁾

∂E ~∂E ∂y ∂p ∂ V ∂U"

∂W2 = ∂y ∂p ∂V ∂U" ∂W2

∂E   ∂E ∂y ∂p

---=--- — (10)

• ∂ W 3  ∂y ∂p ∂ V ∂ W 3

∂E   ∂E ∂y

---=-----—(11)

∂ W 4  ∂y ∂p ∂ W 4

Furthermore, the weight improvement process used the following equation:

Wk. = Wk. + dW, k = 1,2,3,4.

with

dW = m × Wk_j - η_r × (1 - m) × ∂ Wk_j(13)

and m, η_r, ∂Wk_jwith k = 1,2,3,4 respectively stating the parameters of momentum, learning rate, and weight change of Wk, k = 1,2,3,4 based on Equation (8)-(11).

• 4.    Numerical Results

This section gives the numerical results in modeling solar radiation as a dependent variable, y (t), with meteorological variables as independent variables, namely wind speed (x₁), wind direction (x₂) , humidity (x₃), air temperature (x₄),, and air pressure (x₅). Besides meteorological data, to accommodate the influence of solar radiation data from time to time, input data is also provided by solar radiation data at previous times, which are analyzed using the autocorrelation method. The combination of these two input types was simultaneously used to model solar radiation as given by Equation (14) below:

y (^t )=^f

^λ x (t -1), x₂ (t - 2), x₂ (t - 4), x₃ (t - 2), x₃ (t - 4), x₃ (t - 5), x₄ (t - 2),

(14)

V x5( t - 2), y (t-1), y (t - 2), y (t - 3)

The numerical simulation of the proposed model was divided into two types of activation functions in the hidden layer, namely using the hyperbolic tangent function (tanh) and the hyperbolic tangent sigmoid function (tansig) based on Equations (3a and 3b). Furthermore, each model was also simulated with two types of determining the output value, namely the weighted coefficient and the maximum function coefficient of weights, respectively, based on Equations (5) and (6).

The simulation modeling as in Equation (14) for 325 data used 280 training data and 45 testing data).

• 4.1.    The model with hyperbolic tangent activation function (Type I)

The application of the DNN model with the architecture as visualized in Figure 1, with the activation function using a hyperbolic tangent function, and with the output value coefficient using weighted coefficients (Type I-a Model) gave the following results visualized in Figure 2 below.

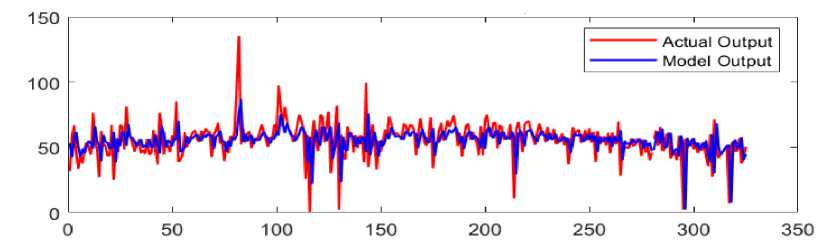
Figure 2. Comparing the output of the DNN model (blue) and the actual data (red) of solar radiation chart pattern Type I-a based on meteorological variables

Applying the DNN model with the activation function using a hyperbolic tangent function and the output value coefficient using the maximum coefficient (Type I-b Model) represented the results in Figure 3.

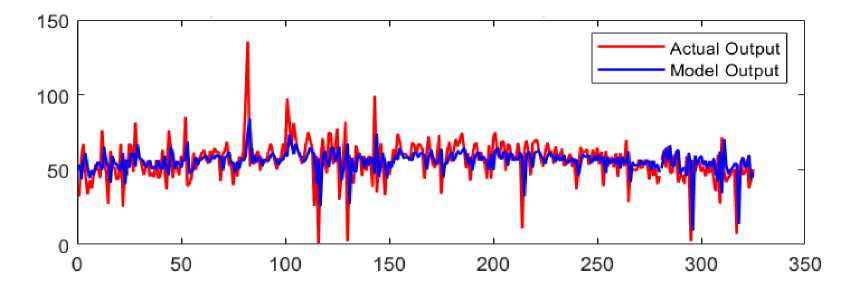
Figure 3. Comparing the output of the DNN model (blue) and the actual data (red) of the solar radiation chart pattern Type I-b based on meteorological variables

Based on statistics, the following statistical measures gave the accuracy of the DNN model for modeling solar radiation built upon the impact of meteorological factors.

Table 1. Comparison of data characteristics based on the type of weighted coefficient on the output value of the Type I DNN Model and its performance

Data/Model	In Sample			Out Sample			Performa (RMSE)
	Min	Mean	Max	Min	Mean	Max	In-Sample	Out-Sample
Type I-a of DNN Model	21.9279	56.3020	87.1276	2.3077	49.4025	68.4165	14.5490	18.6353
Type I-b of DNN Model	25.6257	56.2693	84.3381	9.2312	52.2060	70.5805	14.2802	18.3924
Actual Data	0	57.0206	135.375	2.3077	48.1202	71.5429

In the in-sample data, solar radiation on both models, Type I-a and Type I-b, are 0.7186 lower than the average actual data. Meanwhile, the DNN Type I-b model is 0.7513 lower than the actual data average. In the out-sample data, the mean given by the Type I-a Model and Type I-b Model is higher than the actual data. The average Type I-a model is 1.2823 higher, and the Type I-b model is 4.0858 higher than the actual data. Based on the average indicator, the Type I-a model is relatively preferable to the Type I-b model for both data (in-sample and out-sample).

Table 1 presents the application of the DNN Model to model solar radiation based upon meteorological variables. The performance of the DNN model using the activation function of the hyperbolic tangent function type coefficient of maximum output value (Type I-b Model) is relatively better than the use of weighted coefficients (Type Ia Model) both for in-sample data and out-sample data. The root of mean square error (RMSE) values obtained for the DNN Type I-b model is 18.3924, while the DNN Type I-a model receives an accuracy of 18.6353.

• 4.2.    The model with hyperbolic tangent sigmoid activation function (Type II)

Applying the DNN model with the activation function using a hyperbolic tangent sigmoid function with the output value coefficient using a weighted coefficient (Type II-a Model) gave a result as represented in Figure 4 below.

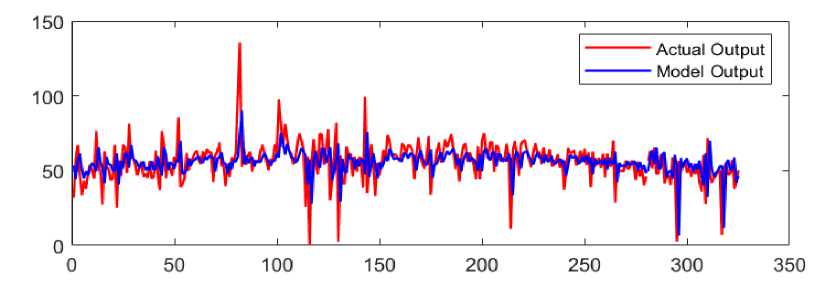
Figure 4. Comparing the DNN Model output (blue) and actual data (red) of solar radiation graphic patterns based on the meteorological variable of Type II-a DNN Model

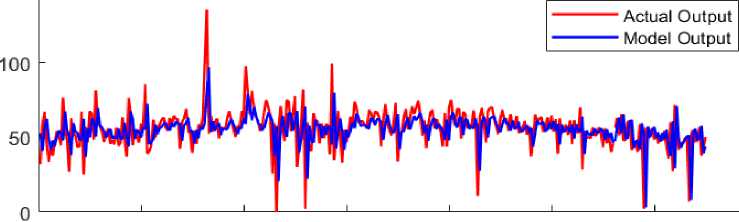
Applying the DNN model with an activation function using a hyperbolic tangent sigmoid function with a coefficient of the output value using the maximum coefficient (Type II-b) gave results as revealed in Figure 5.

150

0        50       100       150       200       250       300       350

Figure 5. Comparing the DNN Model output (blue) and actual data (red) of solar radiation graphic patterns based on meteorological variables of Type II-b DNN Model

Table 2. Comparison of data characteristics based on the type of maximum coefficient on the output value of the Type II DNN Model and its performance

In Sample                  Out Sample          Performa (RMSE)

Data/Model	Min	Mean	Max	Min	Mean	Max	Insample	Out-sample
Type II-a of DNN Model	27.5532	56.3215	90.2840	6.6003	50.9294	69.8383	14.2835	18.4005
Type II-b of DNN Model	20.4482	56.0612	96.8665	3.2770	49.0978	70.7381	14.2802	18.7382
Actual Data	0	57.0206	135.375	2.3077	48.1202	71.5429

In the in-sample data, solar radiation on both models, Type II-a and Type II-b, have a lower average than the actual data. The average intensity of solar radiation given by the DNN Type II-a model is 0.6991 lower than the average actual data. Meanwhile, the DNN Type II-b model is 09594 lower than the average actual data. In the out-sample data, the mean given by the Type II-a Model and the Type II-b Model is higher than the actual data. The mean of the Type II-a Model of 2.8092 and Type II-b Model of 0.9776 is higher than the actual data. Based on the average indicator for the in-sample data, the Type II-a model is relatively better than the Type II-b model.

However, for the out-sample data, the Type II-b model is relatively preferable to the Type II-a model.

Table 2 shows the application of the DNN model to model the solar radiation intensity based on meteorological variables. The performance of the Type II-a DNN model is relatively better than the Type II-b DNN model. The RMSE value of the Type II-a DNN Model is 18.4005, while the Type II-b DNN Model is 18.7382.

Furthermore, Table 1 and Table 2 present the best results for accomplishing the DNN model based on the type of activation function in the hidden layer. The hyperbolic tangent activation function is relatively better than the activation function using the hyperbolic tangent sigmoid function in modeling the data. This can be seen from the performance of the model using RMSE, that the DNN model with activation function using a hyperbolic tangent (Type I Model) with an accuracy of 18.3924, namely the Type I-b DNN Model. Moreover, the DNN Model with the activation function using a hyperbolic tangent sigmoid (Type II DNN Model) has a high performance of 18.4005, namely the Type II-a Model.

Compared to [7] on the same data and subjects research, the comparison of model performance is presented in Table 3.

Table 3. Performance Comparison of the developed DNN model with the Wavelet Neural Network (WNN) [7].

Identity of Model	Compared Indicators
	Training Model		Testing Model
	Mean	RMSE	Mean	RMSE
WNN* Model (Bahri, 2020)	61.8790	16.9941	51.5302	14.7801
Type I-b of the DNN Model	56.3020	14.2802	52.2060	18.3924
Type II-a of the DNN Model	56.3215	14.2835	50.9294	18.4005
Actual Data	57.0206		48.1202

The average and the RMSE indicators in Table 3 reveal that the DNN Model is relatively better than the WNN^* Model in the training model. Furthermore, in the testing model, the DNN Model (Type II-a) average is somewhat better than the WNN^* Model. However, based on the RMSE indicator, the performance of the WNN^* Model is relatively better than the DNN Model developed in this study. Therefore, for further research, a hybrid model will be created between the DNN Model and the Wavelet Method to enhance the performance of the currently developed model.

• 5.    Conclusion

The solar radiation modeling in this study is built upon the Dynamic Neural Network (DNN) Model. The application of the DNN model to the solar radiation intensity model based on variables related to meteorology is simulated using two types of activation functions in the hidden layer, namely the hyperbolic tangent function (Type I Model) and hyperbolic tangent sigmoid (Type II Model). Each type is then distinguished again in determining the output value with a weighted coefficient (Type a) and a maximum coefficient (Type b). The RMSE indicator shows that the application of the DNN model in this study gave quite acceptable results, as seen in the graph pattern of the model output in comparison with the target data, particularly in the in-sample data. Based on the two cases of activation function applied, the DNN model using the hyperbolic tangent activation function is relatively better than the hyperbolic tangent sigmoid type of the activation function.

Acknowledgment

The authors express gratitude to the Chancellor of the University of Mataram for the financial support for this research. We are grateful to the Department of Environment and Forestry of West Nusa Tenggara Province for supplying the data used in this study. The authors are also thankful to all parties who have provided input to improve this research statement answering issues in the previous section and future research work.

References

• [1]    W. T. Shearer, "Infection versus immunity: What's the balance?" Journal of Allergy and Clinical Immunology, vol. 116, no. 2, pp. 263–266, 2005, doi: 10.1016/j.jaci.2005.06.001.

• [2]    Anonim, “NOSEHerbalindo Glosarium,” NoseHerbalindo Laman, 2019. [Online]. Available: https://nose.co.id/ glosarium/ultraviolet

• [3]    J. Tovar-Pescador, "Modelling the statistical properties of solar radiation and proposal of a technique based on boltzmann statistics," Modeling Solar Radiation at the Earth's Surface: Recent Advances, pp. 55–91, 2008, doi: 10.1007/978-3-540-77455-6_3.

• [4]    A. D. Şahin and Z. Şen, "Solar irradiation estimation methods from sunshine and cloud cover data," Modeling Solar Radiation at the Earth's Surface: Recent Advances, pp. 145–173, 2008, doi: 10.1007/978-3-540-77455-6_6.

• [5]    M. Paulescu, "Solar irradiation via air temperature data," Modeling Solar Radiation at the Earth's Surface: Recent Advances, pp. 175–192, 2008, doi: 10.1007/978-3-540-77455-6_7.

• [6]    F. S. Tymvios, S. C. Michaelides, and C. S. Skouteli, "Estimation of surface solar radiation with artificial neural networks," Modeling Solar Radiation at the Earth's Surface: Recent Advances, pp. 221–256, 2008, doi: 10.1007/978-3-540-77455-6_9.

• [7]    S. Bahri, “Modeling of Solar Radiation Using the Wavelet Neural Network Model in Mataram City Lombok Island,” Lontar Komputer: Jurnal Ilmiah Teknologi Informasi, vol. 11, no. 3, p. 178, Dec. 2020, doi: 10.24843/lkjiti.2020.v11.i03.p06.

• [8]    J. Boland, "Time series modeling of solar radiation," Modeling Solar Radiation at the Earth's Surface: Recent Advances, no. 1, pp. 283–312, 2008, doi: 10.1007/978-3-540-77455-6_11.

• [9]    L. Mora-López, "A new procedure to generate solar radiation time series from achine learning theory," Modeling Solar Radiation at the Earth's Surface: Recent Advances, no. 1977, pp. 313–326, 2008, doi: 10.1007/978-3-540-77455-6_12.

• [10]    L. Fortuna, G. Nunnari, and S. Nunnaru, Nonlinear Modeling of Soalar Radiation and Wind Speed Time Series. Switzerland: Springer, 2016. doi: 10.1007/978-3-319-38764-2.

• [11]    A. J. Hussain, P. Liatsis, M. Khalaf, H. Tawfik, and H. Al-Asker, "A Dynamic Neural Network Architecture with Immunology Inspired Optimization for Weather Data Forecasting," Big Data Research, vol. 14, pp. 81–92, Dec. 2018, doi: 10.1016/j.bdr.2018.04.002.

• [12]    M. Akhtar, M. U. G. Kraemer, and L. M. Gardner, "A dynamic neural network model for predicting risk of Zika in real time," BMC Medicine, vol. 17, no. 1, Sep. 2019, doi: 10.1186/s12916-019-1389-3.

• [13]    K. Hami-Eddine, P. Klein, L. Richard, and A. Furniss, "Anomaly detection using dynamic neural networks, classification of prestack data," in Society of Exploration Geophysicists International Exposition and 82nd Annual Meeting 2012, SEG 2012, 2012, pp. 2005–2009. doi: 10.1190/segam2012-1222.1.

• [14]    IEEE Control Systems Society. Chapter Malaysia, Proceedings: 2013 IEEE 9th International Colloquium on Signal Processing and Its Applications, CSPA 2013, 8-10 March 2013, Berjaya Times Square Hotel, Kuala Lumpur, Malaysia.

• [15]    Wu, Di, et al., "Deep Dynamic Neural Networks for Multimodal Gesture Segmentation and Recognition." IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.38, no. 8, 2016, pp.1583-1597, doi: 10.1109/TPAMI.2016.2537340.

• [16]    U. P. Indian Institute of Information Technology (Vārānasi, Institute of Electrical and Electronics Engineers. Uttar Pradesh Section, and Institute of Electrical and Electronics Engineers, 2016 IEEE Uttar Pradesh Section Conference on Electrical, Computer and Electronics Engineering (UPCON): Indian Institute of Technology (Banaras Hindu University), Varanasi, India, Dec 9-11, 2016.

104