Analisis Peramalan Penerimaan Negara Bukan Pajak Menggunakan Metode Grey-Markov Dan ANFIS
on
Majalah Ilmiah Teknologi Elektro, Vol.22, No.1, Jan-Juni 2023.
DOI: https://doi.org/10.24843/MITE.2023.v22i01.P01
1
Analisis PeramalanPenerimaan Negara Bukan Pajak Menggunakan Metode Grey-Markov Dan ANFIS
I Dewa Nyoman Anom Manuaba1, Made Sudarma2, Nyoman Gunantara3
[Submission:30-11-2022, Accepted:24-12-2022]
Abstract — Every year, Udayana University publishes the NonTax State Revenue Target (TPNBP) as a guide for allocating budgetary funds for the T+2 year. The provision of budget allocations for the T+2 year will depend on how accurately the TPNBP is calculated, which will boost efficiency in carrying out budget planning. Due to the limits of the PNBP realization data at Udayana University and the benefits of the ANFIS approach for forecasting stationary data types, it is required to evaluate the merits of the Gray-Markov and ANFIS methods in order to determine which method is more effective. The study's findings reveal that the Grey-Markov approach yields a value of 0.118% while the ANFIS method yields a value of 4.978%. This suggests that while both methods produce extremely precise results, the Grey-Markov method is more accurate than the ANFIS method due to its smaller MAPE value. The MAPE value for the Grey-Markov approach for the SPI acceptance variable is 0.319%, whereas the MAPE value for the ANFIS method is 23.39%, indicating that the Grey-Markov method is more accurate at predicting SPI acceptance.
Keywords : ANFIS; Grey-Markov; Forecasting; PNBP
Intisari — Universitas Udayana setiap tahunnya melaporkan Target Penerimaan Negara Bukan Pajak (TPNBP) sebagai acuan pemberian alokasi anggaran tahun T+2. Ketepatan dalam penentuan TPNBP akan berpengaruh kepada pemberian alokasi anggaran tahun T+2, sehingga dapat meningkatkan optimalisasi dalam melakukan perencanaan anggaran. Keterbatasan data realisasi PNBP di Universitas Udayana dan keunggulan metode ANFIS dalam melakukan peramalan pada tipe data stasioner, memungkinkan peramalan dengan metode Grey-Markov dan ANFIS menghasilkan peramalan yang akurat, untuk itu perlu dibandingkan metode mana yang lebih baik. Hasil dari penelitian ini menunjukan metode Grey-Markov mendapatkan nilai 0,118% sedangkan metode ANFIS mendapatkan nilai 4,978% yang artinya walaupun sama-sama mendapatkan hasil sangat akurat, tetapi metode Grey-Markov mendapatkan nilai MAPE yang lebih kecil yang berarti lebih akurat dibandingkan dengan metode ANFIS. Pada variabel penerimaan SPI, metode Grey-Markov mendapatkan hasil yang sangat akurat dengan nilai MAPE 0,319% sedangkan metode ANFIS mendapatkan hasil yang kurang akurat dengan nilai MAPE 23,39% yang berarti bahwa metode Grey-Markov lebih baik dalam melakukan peramalan penerimaan SPI.
Kata Kunci — ANFIS; Grey-Markov; Forecasting; PNBP
Penerimaan pada negara yang bukan penerimaan pajak biasa disebut dengan PNBP menurut UU RI No. 20 pada Tahun 1997 meliputi penerimaan atas pemanfaatan sumber daya alam, penerimaan atas pelayanan pemerintah, pendapatan dari pengelolaan pendapatan pemerintah seperti kerjasama, pendapatan hasil pengelolaan dari asset yang dipisahkan, pendapatan atas hasil putusan yang merupakan pendapatan pemerintah Pusat yang bukan dari pendapatan pajak dan hasil penerimaan dari denda administrasi, penerimaan hak Pemerintah berupa hibah, serta penerimaan lainnya yang diatur oleh Undang-undang tersendiri [1].
Universitas Udayana sebagai perguruan tinggi tertua di Bali yang sudah memiliki status sebagai Badan Layanan Umum (BLU) memiliki beberapa sumber penerimaan, yaitu Rupiah Murni (RM), Bantuan Operasional Perguruan Tinggi Negeri (BOPTN), dan PNBP. Variabel PNBP pada Universitas Udayana antara lain penerimaan pendidikan, penerimaan kerjasama, penerimaan perbankan dan penerimaan jasa badan layanan umum. Penerimaan pendidikan merupakan variabel PNBP di Universitas udayana yang memiliki penerimaan terbesar. Universitas Udayana yang bernaung di bawah Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi, setiap tahunnya melaporkan Target Penerimaan Negara Bukan Pajak (TPNBP) sebagai acuan pemberian alokasi anggaran tahun T+2. Ketepatan dalam penentuan TPNBP akan berpengaruh kepada pemberian alokasi anggaran tahun T+2, sehingga dapat meningkatkan optimalisasi dalam melakukan perencanaan anggaran. Penentuan TPNBP yang tidak mendekati realisasi penerimaan akan meningkatkan peluang terjadinya revisi anggaran sehingga kurang optimal dalam pemanfaatan waktu pelaksanaan kegiatan. Sampai saat penelitian ini dilakukan, belum ada peraturan Rektor atau panduan mengenai perhitungan TPNBP, sehingga terdapat celah yang cukup besar antara TPNBP dan realisasi penerimaannya.
Teknik dalam memprediksikan suatu nilai pada masa mendatang yang didasarkan pada data di masa lampau ataupun data pada masa kini sebagai acuan dapat disebut sebagai peramalan [2], [3], [12], [4]–[11]. Peramalan menjadi bagian yang sangat vital untuk sebuah organisasi sebagai acuan untuk pengambilan keputusan tingkat manajemen dalam perencanaan jangka pendek maupun jangka panjang suatu perusahaan [3], [13]–[15]. Peramalan dapat diterapkan pada berbagai bidang, seperti administrasi negara, pendidikan,

meteorologi, geofisika, kependudukan, keuangan, ekonomi, pemasaran produk, produksi, dan riset operasional [16].
Penetapan status BLU Universitas Udayana pada tahun 2012, menyebabkan ketersediaan data realisasi PNBP di Universitas Udayana berkisar 5 sampai 10 tahun terakhir dan tipe pola datanya yang mengarah pada pola data horizontal atau stasioner dengan fluktuasi rendah [17]. Keterbatasan data realisasi PNBP ini menjadi latarbelakang pemilihan metode Grey-Markov pada penelitian ini karena keuanggulannya dalam melakukan peramalan dengan kelengkapan data yang tidak lengkap atau ketersediaan jumlah data yang sedikit [1], [2], [18]–[22]. Tipe pola data penerimaan pendidikan di Universitas Udayana yang mengarah pada pola data horizontal atau stasioner dengan fluktuasi rendah, menjadi latarbelakang pemilihan metode ANFIS karena keunggulan metode ANFIS dalam melakukan peramalan pada tipe data stasioner. Peramalan dengan metode Grey-Markov dan ANFIS memungkinkan menghasilkan peramalan yang akurat, untuk itu perlu dibandingkan metode mana yang lebih baik, sehingga dapat memberikan gambaran dalam memperkecil celah antara TPNBP dan realisasi PNBP di Universitas Udayana.
-
II. STUDI PUSTAKA
-
A. Metode Grey-Markov
Metode Grey-Markov adalah pengembangan dari metode Grey yang dikombinasikan dengan menerapkan analisis Rantai Markov [1][23]. Metode Grey-Markov mengunakan konsep perpindahan keadaan dimana kepastian perubahan data dari waktu ke waktu tidak dapat dipastikan. Analisis Rantai Markov membantu menyelesaikan peramalan dari sifat ketidakpastian datanya pada metode Grey [1].
Metode Prediksi Grey merupakan sebuah metode untuk melakukan peramalan yang dapat dilakukan dengan kelengkapan data yang tidak lengkap atau ketersediaan jumlah data yang sedikit [1], [2], [18]–[22]. Metode ini menggunakan satu variabel penelitian di dalam persamaan diferensial orde satu [2]. Untuk menghasilkan peramalan yang valid, tidak dibutuhkan pertimbangan pada distribusi statistik apabila menggunakan metode ini [18][19]. Dibutuhkan minimal empat data historis di dalam interval yang sama apabila menggunakan metode Grey dan tidak memerlukan seluruh data historis. Metode ini memiliki fokus pada sampel data kecil untuk melakukan peramalan dimana data yang kurang lengkap dapat diatasi secara efektif [21]. Metode Grey pada umumnya dikenal sebagai Metode Grey (1,1), yang menunjukan 1 jumlah variabel yang digunakan dan dilakukan 1 kali diferensial [1], [24], [25].
-
B. Metode ANFIS
ANFIS (Adaptive Neuro-fuzzy Inference System) adalah penggabungan mekanisme fuzzy inference system yang digambarkan dalam aristektur jaringan syaraf. Metode ANFIS kebanyakan menggunakan sistem inferensi fuzzy model Takagi-Sugeno-Kang (TSK) dengan orde satu yang mempermudah serta kesederhanaan dalam komputasi [26].
-
C. Tingkat Akurasi
Mean Absolute Percentage Error (MAPE) merupakan salah satu metode perhitungan yang dapat digunakan untuk menghitung tingkat akurasi suatu peramalan [2]. Evaluasi
keakuratan suatu perkiraan populasi paling sering menggunakan metode MAPE sebagai pengukur tingkat akurasinya. Karena memberikan petunjuk seberapa besar nilai aktual atau nilai sebenarnya dibandingkan kesalahan peramalannya. Rata-rata persentase absolut kesalahan dinyatakan dengan metode MAPE dan lebih sering digunakan untuk membandingkan data yang mempunyai nilai skala interval waktu yang berbeda. Semakin kecil nilai MAPE, maka hasil peramalan dikatakan semakin akurat [27]. Perhitungan akurasi menggunakan MAPE dapat dilihat pada persamaan (1) [27][28][14][29].
λ≡γ = (1∑M¾Γ¾-t 100 (1)
Nilai MAPE didapat dari penjumlahan total nilai aktual dikurangi nilai prediksi, kemudian dibagi dengan nilai aktual dan hasilnya dikalikan dengan 100, dimana y(t) merupakan nilai aktual dan y'(t) merupakan nilai prediksi. Hasil yang didapat merupakan nilai persentase MAPE yang menunjukan tingkat akurasi. Nilai MAPE di bawah 10% berarti tingkat akurasi tergolong sangat akurat. Nilai MAPE berkisar antara 10% sampai 20% berarti tingkat akurasi tergolong akurat. Nilai MAPE berkisar antara 20% sampai 50% berarti tingkat akurasi tergolong kurang akurat dan nilai MAPE diatas 50% berarti tingkat akurasi tergolong tidak akurat, seperti terlihat pada Tabel I.
TABEL I
TINGKAT AKURASI MAPE
|
MAPE (%) |
Tingkat Akurasi |
|
< 10 |
Sangat Akurat |
|
10 - 20 |
Akurat |
|
20 - 50 |
Kurang Akurat |
|
> 50 |
Tidak Akurat |
Sumber: [2][27][29]
Skematik penelitian pada penelitian ini dirancang dilakukan dalam beberapa tahap, yaitu pengumpulan data PNBP di Universitas Udayana, melakukan peramalan TPNBP dengan menggunakan metode Grey-Markov dan metode ANFIS, melakukan pengukuran tingkat akurasi peramalannya, membandingkan tingkat akurasi yang didapat dan memberikan rekomendasi metode peramalan yang lebih baik dalam penyusunan TPNBP, seperti terlihat pada Gambar 1.
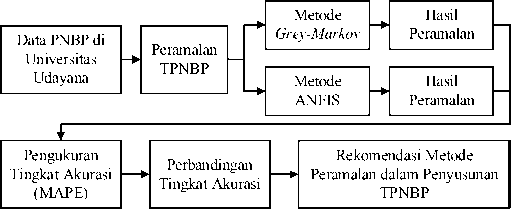
Gambar 1. Skematik Penelitian
Data PNBP di Universitas Udayana digunakan sebagai dasar penyusunan Target Penerimaan Negara Bukan Pajak (TPNBP). Metode peramalan yang digunakan adalah metode Grey-Markov dan ANFIS. Hasil dari peralaman yang dilakukan diukur tingkat akurasi peramalannya dengan metode MAPE yang dapat dibagi menjadi empat, yaitu sangat akurat, akurat, kurang akurat, dan tidak akurat. Tingkat akurasi masing-masing metode peramalan kemudian dibandingkan, metode dengan tingkat akurasi paling baik akan direkomendasikan sebagai metode peramalan yang diterapkan dalam penyusunan TPNBP di Universitas Udayana.
-
A. Grafik Time Series Data Aktual
Data yang digunakan pada penelitian ini yaitu data realisasi penerimaan negara bukan pajak Universitas Udayana yang bersumber dari penerimaan pendidikan. Analisis time series memiliki tujuan agar dapat memprediksi peristiwa yang akan datang dengan memahami, menafsirkan dan mengevaluasi perubahan yang terjadi [30]–[32]. Data yang diambil merupakan data time series atau data runtun waktu berdasarkan tahun, yaitu realisasi penerimaan UKT dari tahun 2016-2021 dan realisasi penerimaan SPI tahun 2018-2021, seperti terlihat pada Tabel II.
TABEL II
DATA REALISASI PNBP UNIVERSITAS UDAYANA
|
No |
Tahun |
Jumlah Mahasiswa |
Penerimaan Pendidikan (Rp) | |
|
UKT |
SPI | |||
|
1 |
2016 |
50.151 |
241.755.370.877 |
- |
|
2 |
2017 |
47.871 |
258.938.302.504 |
- |
|
3 |
2018 |
50.116 |
295.248.035.504 |
62.859.288.800 |
|
4 |
2019 |
49.804 |
304.977.873.501 |
75.192.369.891 |
|
5 |
2020 |
51.193 |
320.992.204.000 |
64.903.815.000 |
|
6 |
2021 |
52.534 |
341.690.982.009 |
60.758.318.000 |
Penerimaan UKT setiap tahunnya mengalami peningkatan jumlah realisasi penerimaannya, sedangkan penerimaan SPI terjadi peningkatan pada tahun 2019 kemudian turun setiap tahunnya hingga tahun 2021, seperti dapat dilihat pada Gambar 2 dan Gambar 3.
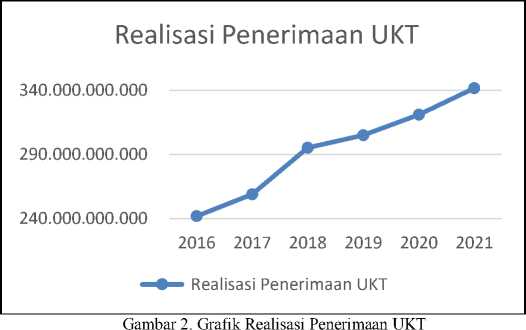
Gambar 2 memperlihatkan pola data penerimaan UKT adalah pola data trend meningkat dimana setiap tahunnya terjadi peningkatan realisasi penerimaan UKT.
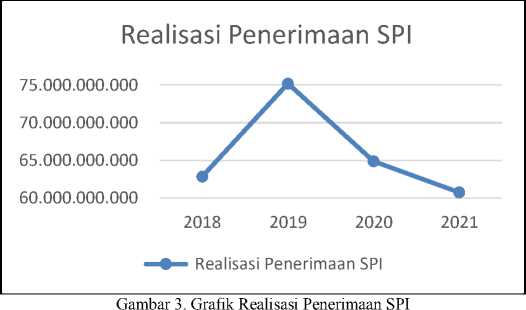
Gambar 3 memperlihatkan pola data penerimaan SPI adalah pola data fluktuatif dimana terjadi peningkatan dan penurunan yang cukup besar pada realisasi penerimaan SPI.
Data yang digunakan untuk pelatihan peramalan pada penerimaan UKT yaitu data penerimaan UKT tahun 2016 sampai tahun 2020, sedangkan penerimaan UKT tahun 2021 digunakan untuk uji tingkat akurasi peramalan. Data yang digunakan untuk pelatihan peramalan pada penerimaan SPI yaitu data penerimaan SPI tahun 2018 sampai tahun 2020, sedangkan penerimaan SPI tahun 2021 digunakan untuk uji tingkat akurasi peramalan.
-
B. Peramalan Metode Grey-Markov
Peramalan menggunakan metode Grey-Markov melibatkan hasil prediksi dari metode Grey (1,1) yang akan dimodifikasi menggunakan analisis rantai Markov (Markov Chain). Hasil peramalan dari metode Grey (1,1) akan menjadi sebuah barisan data baru. Selanjutnya akan ditentukan jumlah keadaan (state) dan batasan dari setiap keadaan tersebut berdasarkan nilai error relative.
Nilai prediksi yang didapat setelah melakukan perhitungan menggunakan metode Grey-Markov dapat dilihat pada Gambar 4 dan Gambar 5.

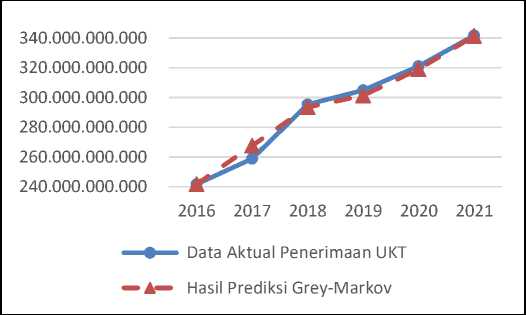
Gambar 4. Grafik Perbandingan Data Aktual dan metode Grey-Markov untuk Penerimaan UKT
Gambar 4 memperlihatkan grafik hasil prediksi Grey-Markov terdapat beberapa jarak tetapi tetap mendekati garis data aktual yang berarti hasil prediksi Grey-Markov mendekati nilai aktualnya untuk penerimaan UKT. Pada tahun 2016, hasil prediksi metode Grey-Markov lebih rendah dari data aktual, kemudian di tahun 2017 lebih tinggi dari data aktualnya. Pada tahun 2018 kembali lebih rendah dari data aktualnya hingga tahun 2020, kemudian pada tahun 2021 mulai mendekati data aktualnya.
Hasil prediksi penerimaan UKT metode Grey-Markov pada tahun 2021 mengalami peningkatan dibanding tahun 2020 disebabkan karena prediksi keadaan pada tahun 2021 untuk penerimaan UKT terjadi peningkatan.
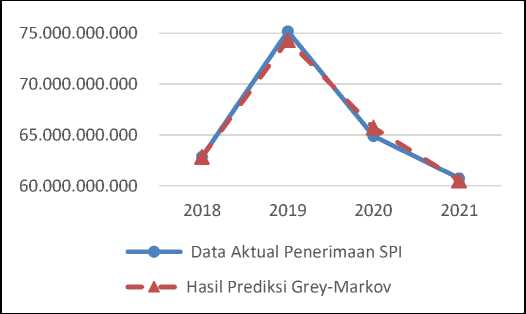
Gambar 5. Grafik Perbandingan Data Aktual dan metode Grey-Markov untuk Penerimaan SPI
Gambar 5 memperlihatkan bahwa grafik hasil prediksi metode Grey-Markov terdapat beberapa jarak tetapi tetap mendekati garis data aktual yang berarti hasil prediksi Grey-Markov mendekati nilai aktualnya untuk penerimaan SPI. Pada tahun 2018, hasil prediksi metode Grey-Markov lebih rendah dari data aktual hingga tahun 2019, kemudian di tahun 2020 lebih tinggi dari data aktualnya dan pada tahun 2021 lebih rendah dari data aktual tetapi jaraknya sudah mendekati data aktualnya.
Hasil prediksi penerimaan SPI metode Grey-Markov pada tahun 2021 mengalami penurunan dibanding tahun 2020 disebabkan karena prediksi keadaan pada tahun 2021 untuk penerimaan SPI terjadi penurunan.
Penerimaan UKT dan penerimaan SPI yang diuji yaitu pada tahun 2021, dimana data asli yang digunakan untuk penerimaan UKT adalah data mulai tahun 2016-2020. Maka dari itu, jumlah
transisi dari tahun 2016 ke tahun 2021 untuk penerimaan UKT adalah lima kali transisi. Untuk penerimaan SPI, data asli yang digunakan adalah data mulai tahun 2018-2020, maka dari itu jumlah transisi dari tahun 2018 ke tahun 2021 untuk penerimaan SPI adalah tiga kali transisi.
Hasil prediksi penerimaan UKT dan penerimaan SPI tahun 2021 berdasarkan metode Grey-Markov ditampilkan pada Tabel III.
TABEL III
HASIL PREDIKSI TAHUN 2021 METODE GREY-MARKOV
|
Tahun |
Penerimaan UKT |
Penerimaan SPI |
|
2021 |
341.286.954.463,84 |
60.564.779.811,73 |
Berdasarkan hasil prediksi dari metode Grey-Markov yang ditampilkan pada Tabel III, maka langkah selajutnya adalah menguji seberapa akurat hasil prediksi dengan membandingkan data aktual yang telah kita miliki sebelumnya. Metode dalam menghitung tingkat akurasi yang digunakan dalam penelitian ini adalah MAPE (Mean Absolute Percentage Error) berdasarkan Persamaan (1). Hasil uji akurasi prediksi oleh metode Grey-Markov ditampilkan pada Tabel IV.
TABEL IV
TINGKAT AKURASI PERAMALAN METODE GREY-MARKOV
|
Variabel |
MAPE (Persen) |
Keterangan |
|
Penerimaan UKT |
0,118 |
Sangat Akurat |
|
Penerimaan SPI |
0,319 |
Sangat Akurat |
Tabel IV menunjukkan bahwa nilai uji MAPE untuk variabel penerimaan UKT dan penerimaan SPI kurang dari 10 Persen artinya hasil peramalan sangat akurat untuk peramalan metode Grey-Markov. Dari hasil tingkat akurasi tersebut menunjukkan bahwa metode Grey-Markov pada peramalan penerimaan UKT dan penerimaan SPI bekerja dengan sangat baik.
-
C. Peramalan Metode ANFIS
-
1) Penentuan Input dan Target Output
Nilai input pada peramalan metode ANFIS ini menggunakan data pada Tabel II dan nilai target output menggunakan nilai prediksi Grey-Markov. Untuk peramalan penerimaan UKT, menggunakan input jumlah mahasiswa dan realisasi penerimaan UKT, target output menggunakan nilai prediksi Grey-Markov untuk penerimaan UKT. Kombinasi input dan target output untuk peramalan penerimaan UKT dapat dilihat pada Tabel V.
TABEL V
KOMBINASI INPUT DAN TARGET OUTPUT PENERIMAAN UKT
|
Tahun |
Input |
Target Output | |
|
Jumlah Mahasiswa |
Penerimaan UKT | ||
|
2016 |
50.151 |
241.755.370.877 |
241.742.874.744 |
|
2017 |
47.871 |
258.938.302.504 |
267.550.199.636 |
|
2018 |
50.116 |
295.248.035.504 |
293.519.221.135 |
|
2019 |
49.804 |
304.977.873.501 |
301.380.178.924 |
|
2020 |
51.193 |
320.992.204.000 |
318.980.854.665 |
TABEL VI
KOMBINASI INPUT DAN TARGET OUTPUT PENERIMAAN SPI
|
Tahun |
Input |
Target Output | |
|
Jumlah Mahasiswa |
Penerimaan SPI | ||
|
2018 |
50.116 |
62.859.288.800 |
62.860.752.824 |
|
2019 |
49.804 |
75.192.369.891 |
74.328.327.514 |
|
2020 |
51.193 |
64.903.815.000 |
65.746.242.845 |
Untuk peramalan penerimaan SPI, menggunakan input jumlah mahasiswa dan realisasi penerimaan SPI, target output menggunakan nilai prediksi Grey-Markov untuk penerimaan SPI. Kombinasi input dan target output untuk peramalan penerimaan SPI dapat dilihat pada Tabel VI.
-
2) Pelatihan Metode
Pelatihan metode peramalan ANFIS ini menggunakan
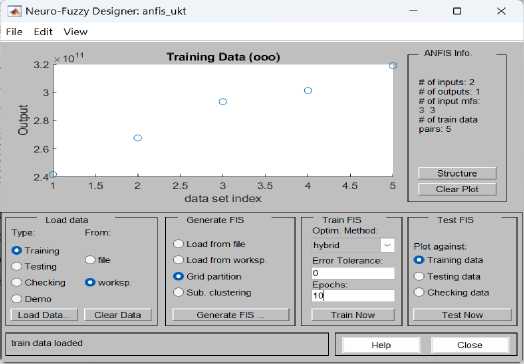
bantuan aplikasi MatLab yang sudah memiliki modul ANFIS. Langkah pertama yang dilakukan adalah memanggil data yang sudah disiapkan. Hasil pemanggilan data untuk penerimaan UKT dapat dilihat pada Gambar 6 dan untuk penerimaan SPI dapat dilihat pada Gambar 7.
Gambar 6 memperlihatkan data input penerimaan UKT memiliki pola data trend yang cenderung meningkat. Jumlah data yang digunakan untuk penerimaan UKT adalah 5 baris data.
Gambar 6. Pemanggilan Data untuk Penerimaan UKT
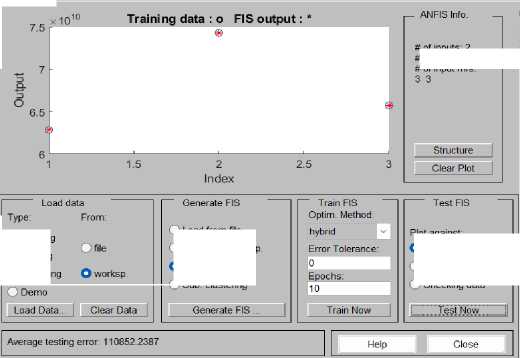
Sedangkan Gambar 7 memperlihatkan bahwa data input penerimaan SPI memiliki pola data yang fluktuatif naik dan turun. Jumlah data yang digunakan untuk penerimaan SPI adalah 3 baris data.
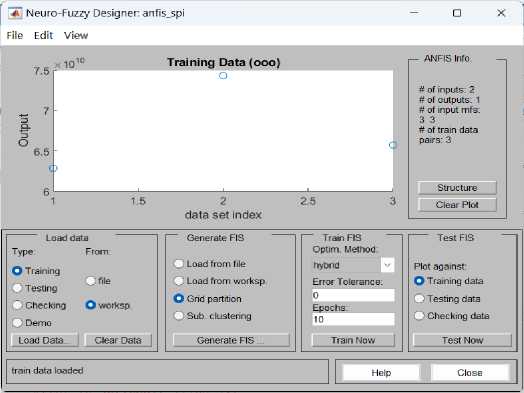
Gambar 7. Pemanggilan Data untuk Penerimaan SPI
Struktur yang dihasilkan dari kombinasi input dan target output metode ANFIS dapat dilihat pada Gambar 8. Terlihat bahwa struktur ANFIS terdiri dari dua input, dengan masing-masing terdiri dari 3 Membership Function. Terdapat rule sebanyak 9 buah, dengan operator and. ANFIS terdiri dari satu output dengan output MF yang terbentuk sebanyak 9 buah. Garis-garis yang menghubungkan antar node menunjukkan sebuah rule yang bersesuaian.
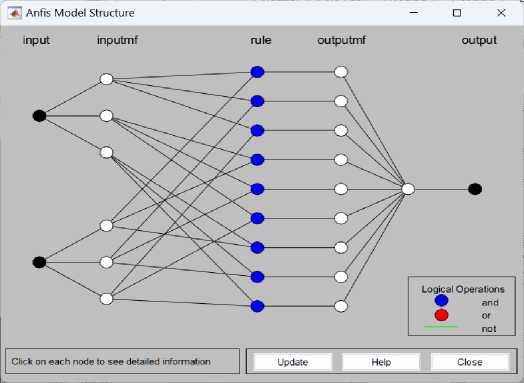
Gambar 8. Struktur Metode ANFIS
Pada pelatihan ini, penentuan derajat keanggotaannya menggunakan fungsi anggota generallized bell. Toleransi error yang diinginkan adalah 0 dan epochs atau perulangan pelatihan menggunakan 10 kali, sehingga didapatkan hasil pelatihan seperti pada Gambar 9 dan Gambar 10.

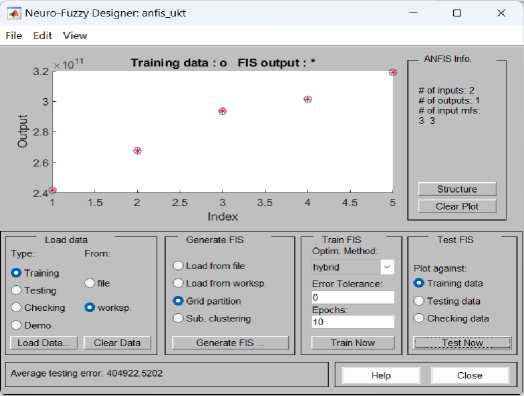
Gambar 9. Hasil Pelatihan Data ANFIS Penerimaan UKT
Grafik perbandingan data aktual dengan data hasil prediksi metode ANFIS disajikan pada Gambar 11 dan Gambar 12.
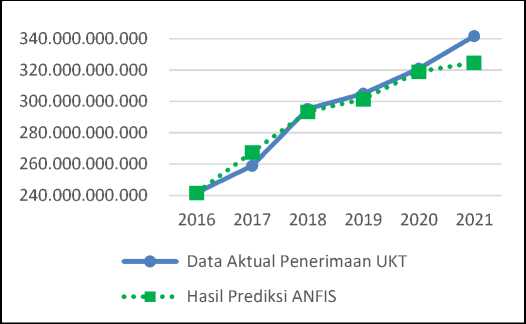
Gambar 11. Grafik Perbandingan Data Aktual dan metode ANFIS untuk Penerimaan UKT
Gambar 9 memperlihatkan pelatihan penerimaan UKT dan Gambar 10 memperlihatkan pelatihan penerimaan SPI menghasilkan data input dan output hasil pelatihan terdapat pada titik yang hampir sama, artinya ANFIS yang kita latih telah dapat memetakan input terhadap output dengan baik.
File Edit View
∣ 3 Neuro-Fuzzy Designer anfis_spi
OTraining
OTesting
□ptιm. Method:
Gambar 10. Hasil Pelatihan Data ANFIS Penerimaan SPI
# ot inputs: 2
# of outputs: 1 # of input mfs:
O Load from file O Load from w□rksp O Grid partition O Sub. clustering
Plot against: ©Training data OTesting data C ' Checking data
-
3) Pengujian
Setelah melakukan pelatihan dan mendapatkan ANFIS yang kita latih telah dapat memetakan input terhadap output dengan baik, selanjutnya melakukan peramalan tahun 2021 untuk penerimaan UKT dan penerimaan SPI. Untuk penerimaan UKT, menggunakan jumlah mahasiswa sebanyak 52.534 dan Penerimaan UKT sejumlah 341.690.982.009. Untuk penerimaan SPI, menggunakan jumlah mahasiswa sebanyak 52.534 dan Penerimaan SPI sejumlah 60.758.318.000. Hasil dari peramalan menggunakan metode ANFIS yang telah dibuat sebelumnya dapat dilihat pada Tabel VII.
TABEL VII
HASIL PREDIKSI TAHUN 2021 METODE ANFIS
|
Tahun |
Penerimaan UKT |
Penerimaan SPI |
|
2021 |
324.681.955.164 |
74.969.767.994 |
Gambar 11 memperlihatkan bahwa garis hasil prediksi ANFIS terdapat beberapa jarak tetapi tetap mendekati garis data aktual kecuali pada tahun 2021 yang terpaut cukup jauh. Pada tahun 2016, hasil prediksi metode Grey-Markov lebih rendah dari data aktual, kemudian di tahun 2017 lebih tinggi dari data aktualnya. Pada tahun 2018 kembali lebih rendah dari data aktualnya hingga tahun 2020, kemudian pada tahun 2021 menurun cukup jauh.
Hasil prediksi penerimaan UKT metode ANFIS pada tahun 2021 mengalami peningkatan dibanding tahun 2020 disebabkan karena sifat metode ANFIS yang mengikuti kebiasaan dari data latih yang digunakan, yaitu cenderung mengalami peningkatan sehingga menghasilkan prediksi penerimaan UKT tahun 2021 sebesar 324.681.955.164.
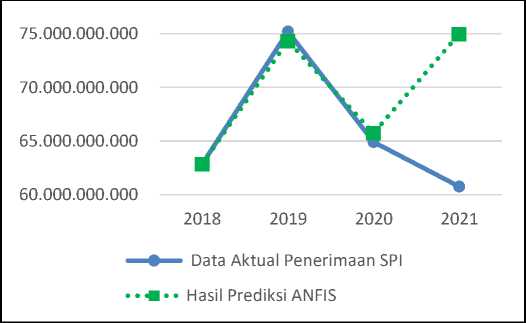
Gambar 12. Grafik Perbandingan Data Aktual dan metode ANFIS untuk Penerimaan SPI
Gambar 12 memperlihatkan bahwa garis hasil prediksi ANFIS terdapat beberapa jarak tetapi tetap mendekati garis data aktualnya kecuali pada tahun 2021 yang terpaut sangat jauh. Pada tahun 2018, hasil prediksi metode Grey-Markov lebih rendah dari data aktual hingga tahun 2019, kemudian di tahun 2020 lebih tinggi dari data aktualnya dan pada tahun 2021 lebih tinggi sangat jauh dari data aktualnya.
Hasil prediksi penerimaan SPI metode ANFIS pada tahun 2021 mengalami peningkatan dibanding tahun 2020 disebabkan karena sifat metode ANFIS yang mengikuti kebiasaan dari data
latih yang digunakan, yaitu cenderung mengalami penurunan sehingga menghasilkan prediksi penerimaan SPI tahun 2021 sebesar 74.969.767.994.
Selanjutnya adalah menguji seberapa akurat hasil prediksi dengan membandingkan data aktual yang telah kita miliki sebelumnya. Metode dalam menghitung tingkat akurasi yang digunakan dalam penelitian ini adalah MAPE (Mean Absolute Percentage Error) berdasarkan Persamaan (1). Hasil uji akurasi prediksi oleh metode ANFIS ditampilkan pada Tabel VIII.
TABEL VIII
TINGKAT AKURASI PERAMALAN METODE ANFIS
|
Variabel |
MAPE (Persen) |
Keterangan |
|
Penerimaan UKT |
4,978 |
Sangat Akurat |
|
Penerimaan SPI |
23,390 |
Kurang Akurat |
Tabel VIII menunjukkan bahwa nilai uji MAPE untuk variabel penerimaan UKT kurang dari 10 persen artinya hasil peramalan sangat akurat, sedangkan untuk variabel penerimaan SPI, nilai uji MAPE diatas 20 persen yang artinya hasil peramalannya kurang akurat. Dari hasil tingkat akurasi tersebut menunjukkan bahwa metode ANFIS pada peramalan penerimaan UKT bekerja dengan sangat baik dan pada penerimaan SPI bekerja kurang baik.
-
D. Perbandingan Tingkat Akurasi Peramalan
Grafik perbandingan data aktual dengan data hasil prediksi metode Grey-Markov dan hasil prediksi metode ANFIS disajikan pada Gambar 13 dan Gambar 14.
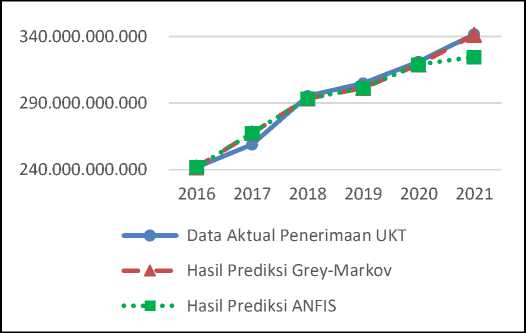
Gambar 13. Grafik Perbandingan Data Aktual, Hasil Prediksi Metode Grey-Markov, dan Hasil Prediksi Metode ANFIS untuk Penerimaan UKT
Gambar 13 memperlihatkan bahwa garis hasil prediksi Grey-Markov terdapat beberapa jarak tetapi tetap mendekati garis data aktual yang berarti hasil prediksi Grey-Markov mendekati nilai aktualnya untuk penerimaan UKT. Pada tahun 2016, hasil prediksi metode Grey-Markov lebih rendah dari data aktual, kemudian di tahun 2017 lebih tinggi dari data aktualnya. Pada tahun 2018 kembali lebih rendah dari data aktualnya hingga tahun 2020, kemudian pada tahun 2021 mulai mendekati data aktualnya. Sedangkan garis hasil prediksi ANFIS terdapat
beberapa jarak tetapi tetap mendekati garis data aktual kecuali pada tahun 2021 yang terpaut cukup jauh. Pada tahun 2016, hasil prediksi metode Grey-Markov lebih rendah dari data aktual, kemudian di tahun 2017 lebih tinggi dari data aktualnya. Pada tahun 2018 kembali lebih rendah dari data aktualnya hingga tahun 2020, kemudian pada tahun 2021 menurun cukup
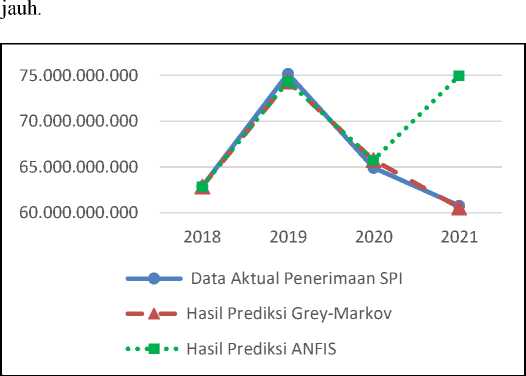
Gambar 14. Grafik Perbandingan Data Aktual, Hasil Prediksi Metode Grey-Markov, dan Hasil Prediksi Metode ANFIS untuk Penerimaan SPI
Gambar 14 memperlihatkan bahwa garis hasil prediksi Grey-Markov terdapat beberapa jarak tetapi tetap mendekati garis data aktual yang berarti hasil prediksi Grey-Markov mendekati nilai aktualnya untuk penerimaan SPI. Pada tahun 2018, hasil prediksi metode Grey-Markov lebih rendah dari data aktual hingga tahun 2019, kemudian di tahun 2020 lebih tinggi dari data aktualnya dan pada tahun 2021 lebih rendah dari data aktual tetapi jaraknya sudah mendekati data aktualnya. Sedangkan garis hasil prediksi ANFIS terdapat beberapa jarak tetapi tetap mendekati garis data aktualnya kecuali pada tahun 2021 yang terpaut sangat jauh. Pada tahun 2018, hasil prediksi metode Grey-Markov lebih rendah dari data aktual hingga tahun 2019, kemudian di tahun 2020 lebih tinggi dari data aktualnya dan pada tahun 2021 lebih tinggi sangat jauh dari data aktualnya.
Perbandingan tingkat akurasi peramalan metode Grey-Markov dengan metode ANFIS dapat dilihat pada Tabel IX.
TABEL IX
PERBANDINGAN TINGKAT AKURASI PERAMALAN
|
Variabel |
Metode Grey-Markov |
Metode ANFIS | ||
|
MAPE (Persen) |
Keterangan |
MAPE (Persen) |
Keterangan | |
|
Penerimaan |
0,118 |
Sangat |
4,978 |
Sangat |
|
UKT |
Akurat |
Akurat | ||
|
Penerimaan |
0,319 |
Sangat |
23,39 |
Kurang |
|
SPI |
Akurat |
Akurat | ||
Tabel IX memperlihatkan bahwa untuk variabel penerimaan UKT, metode Grey-Markov dan metode ANFIS sama-sama p-ISSN:1693 – 2951; e-ISSN: 2503-2372

mendapatkan hasil yang sangat akurat. Dibandingan dari nilai MAPE yang didapat, metode Grey-Markov mendapatkan nilai 0,118% sedangkan metode ANFIS mendapatkan nilai 4,978% yang artinya walaupun sama-sama mendapatkan hasil sangat akurat, tetapi metode Grey-Markov mendapatkan nilai MAPE yang lebih kecil yang berarti lebih akurat dibandingkan dengan metode ANFIS dalam perhitungan peramalan penerimaan UKT, sehingga metode Grey-Markov lebih baik dalam melakukan peramalan penerimaan UKT.
Pada variabel penerimaan SPI, metode Grey-Markov mendapatkan hasil yang sangat akurat dengan nilai MAPE 0,319% sedangkan metode ANFIS mendapatkan hasil yang kurang akurat dengan nilai MAPE 23,39% yang berarti bahwa metode Grey-Markov lebih baik dalam melakukan peramalan penerimaan SPI.
Metode Grey-Markov lebih baik dalam melakukan peramalan penerimaan UKT dan penerimaan SPI dibandingkan metode ANFIS disebabkan karena jumlah data yang tersedia sedikit, ini sesuai dengan penelitian sebelumnya yang menunjukan bahwa metode Grey-Markov memiliki keunggulan dalam melakukan peramalan dengan sumber data yang sedikit [1], [2], [17]–[22], [33]. Metode Grey-Markov memberikan hasil prediksi yang baik pada data yang memiliki nilai fluktuasi yang cukup besar [1], terbukti pada hasil peramalan pada penerimaan SPI dengan data yang nilai fluktiasinya yang cukup besar.
Metode ANFIS dapat bekerja dengan baik apabila terdapat banyak data sampel [26], [34], [35] dan tipe data yang bersifat bersifat stasioner, sehingga pada peramalan penerimaan UKT dan SPI dengan data yang sedikit, metode ANFIS mendapatkan hasil yang tidak lebih baik dibandingkan metode Grey-Markov.
Dari hasil pembahasan di atas dapat disimpulkan bahwa metode Grey-Markov mendapatkan nilai MAPE sebesar 0,118 % pada peramalan penerimaan UKT dan 0,319% pada peramalan penerimaan SPI yang masuk kategori sangat akurat. Metode ANFIS mendapatkan nilai MAPE sebesar 4,978% pada peramalan penerimaan UKT yang masuk kategori sangat akurat dan 23,39% pada peramalan penerimaan SPI yang masuk kategori kurang akurat.
Pada variabel penerimaan UKT, metode Grey-Markov dan metode ANFIS sama-sama mendapatkan hasil yang sangat akurat. Dibandingan dari nilai MAPE yang didapat, metode Grey-Markov mendapatkan nilai 0,118% sedangkan metode ANFIS mendapatkan nilai 4,978% yang artinya walaupun sama-sama mendapatkan hasil sangat akurat, tetapi metode Grey-Markov mendapatkan nilai MAPE yang lebih kecil yang berarti lebih akurat dibandingkan dengan metode ANFIS dalam perhitungan peramalan penerimaan UKT, sehingga metode Grey-Markov lebih baik dalam melakukan peramalan penerimaan UKT.
Pada variabel penerimaan SPI, metode Grey-Markov mendapatkan hasil yang sangat akurat dengan nilai MAPE 0,319% sedangkan metode ANFIS mendapatkan hasil yang kurang akurat dengan nilai MAPE 23,39% yang berarti bahwa metode Grey-Markov lebih baik dalam melakukan peramalan penerimaan SPI.
Metode Grey-Markov dapat direkomendasikan untuk dapat digunakan sebagai metode peramalan penerimaan UKT dan penerimaan SPI di Universitas Udayana.
Referensi
-
[1] A. Ahdika, “Model Grey (1,1) dan Grey-Markov pada Peramalan
Realisasi Penerimaan Negara,” J. Fourier, vol. 7, no. 1, pp. 1–12, 2018, doi: 10.14421/fourier.2018.71.1-12.
-
[2] L. Latipah, S. Wahyuningsih, and S. Syaripuddin, “Peramalan
Pendapatan Asli Daerah Provinsi Kalimantan Timur Menggunakan Model Grey-Markov (1,1),” Jambura J. Math., vol. 1, no. 2, pp. 89– 103, 2019, doi: 10.34312/jjom.v1i2.2347.
-
[3] Ida Ayu Masyuni, “Peramalan Menggunakan Metode Holt-Winters
Untuk Pengujian Kendaraan Bermotor (Studi Kasus: Pengujian Kendaraan Bermotor Kabupaten Tabanan),” J. SPEKTRUM, vol. 6, no. 3, pp. 27–34, 2019.
-
[4] A. Aryati, I. Purnamasari, and Y. N. Nasution, “Peramalan dengan
Menggunakan Metode Holt-Winters Exponential Smoothing (Studi Kasus: Jumlah Wisatawan Mancanegara yang Berkunjung Ke Indonesia) Forecasting using the method of Holt-Winters Exponential Smoothing (Case Study: Number of Foreign Tourists Visi,” J. EKSPONENSIAL, vol. 11, no. 1, pp. 99–105, 2020.
-
[5] F. A. Widjajati and E. Fani, “Menentukan Penjualan Produk Terbaik
di Perusahaan X Dengan Metode Winter Eksponensial Smoothing Dan Metode Event Based,” Limits J. Math. Its Appl., vol. 14, no. 1, pp. 25–35, 2017, [Online]. Available:
http://iptek.its.ac.id/index.php/limits/article/view/2127.
-
[6] W. Handoko, “Prediksi Jumlah Penerimaan Mahasiswa Baru Dengan
Metode Single Exponential Smoothing (Studi Kasus: Amik Royal Kisaran),” JURTEKSI (Jurnal Teknol. dan Sist. Informasi), vol. 5, no. 2, pp. 125–132, 2019, doi: 10.33330/jurteksi.v5i2.356.
-
[7] Y. Asri and D. Permana, “Peramalan Penerimaan Pajak Negara
Indonesia Tahun 2019 Menggunakan Metode Pemulusan
Eksponensial Ganda Tipe Brown,” UNP J. Math., pp. 70–74, 2019, [Online]. Available:
http://ejournal.unp.ac.id/students/index.php/mat/article/view/6321% 0Ahttp://ejournal.unp.ac.id/students/index.php/mat/article/viewFile/ 6321/3228.
-
[8] I. G. N. R. D. Widhura, M. Sudarma, and R. S. Hartati, “Penentuan
Target Pajak Kendaraan Bermotor Di Provinsi Bali Menggunakan ARIMA Dan Algoritma Genetik,” Maj. Ilm. Teknol. Elektro, vol. 17, no. 3, pp. 345–352, 2018, doi: 10.24843/mite.2018.v17i03.p07.
-
Y. Pramana, R. S. Hartati, and K. Oka Saputra, “Peramalan Penerbitan Ijin Mendirikan Bangunan Dengan Single Moving Average Dan Exponential Smoothing,” Maj. Ilm. Teknol. Elektro, vol. 18, no. 2, pp. 241–248, 2019, doi: 10.24843/mite.2019.v18i02.p13.
-
T. N. Putri, A. Yordan, and D. H. Lamkaruna, “Peramalan Penerimaan Mahasiswa Baru Universitas Samudra Menggunakan Metode Regresi Linear Sederhana,” J-TIFA (Jurnal Teknol. Inform., vol. 2, no. 1, pp. 21–27, 2019.
-
S. Sutrisman, H. Syafwan, and ..., “Implementation of Trend Moment Method in Forecasting Regional Income,” Build. Informatics, Technol. Sci., vol. 4, no. 2, pp. 749–758, 2022, doi:
10.47065/bits.v4i2.2090.
-
F. P. Wahyu, I. D. Rahmawati, and K. Umam, “Identifying Best Method for Forecasting Tax Income using Time Series Analysis,” IAPA Int. Conf. Int. Indones. Conf. Interdiscip. Stud., vol. Dec, pp. 60–73, 2022.
-
I. Fitria, M. S. K. Alam, and S. Subchan, “Perbandingan Metode ARIMA dan Exponential Smoothing pada Peramalan Harga Saham LQ45 Tiga Perusahaan dengan Nilai Earning Per Share (EPS) Tertinggi,” Limits J. Math. Its Appl., vol. 14, no. 2, pp. 113–125, 2017, doi: 10.12962/limits.v14i2.3060.
-
Y. Surya Bhakti, A. Budiman Kusdinar, D. Asril, and A. Sunarto, “Model Peramalan Penerimaan Calon Mahasiswa Menggunakan Metode Regresi,” J. Ilm. Komput., vol. 16, no. 2, pp. 113–120, 2020. A. R. Lasri Nijal, Roki Hardianto, “Peramalan Penerimaan Karyawan PT . Cipta Persada Infrastruktur Menggunakan Monte Carlo,” J. Sist. Inf., vol. 3, no. 2, pp. 98–115, 2020.
-
D. A. Setiawan, S. Wahyuningsih, and R. Goejantoro, “Peramalan Produksi Kelapa Sawit Menggunakan Winter’s dan Pegel’s Exponential Smoothing dengan Pemantauan Tracking Signal,” Jambura J. Math., vol. 2, no. 1, pp. 1–14, 2020, doi: 10.34312/jjom.v2i1.2320.
-
[9]
-
[10]
-
[11]
[12]
[13]
[14]
[15]
[16]
-
-
[17] I. D. N. Anom Manuaba, I. B. Gede Manuaba, and M. Sudarma, [35]
C. B. Sinaga, H. Haviluddin, H. S. Pakpahan, A. Prafanto, and H. J. Setyadi, “Peramalan Curah Hujan Dengan Pendekatan Adaptive Neuro Fuzzy Inference System,” Sains, Apl. Komputasi dan Teknol. Inf., vol. 1, no. 2, p. 1, 2019, doi: 10.30872/jsakti.v1i2.2599.
“Komparasi Metode Peramalan Grey dan Grey- Markov untuk mengetahui Peramalan PNBP di Universitas Udayana,” vol. 21, no. 1, pp. 83–88, 2022.
-
[18] A. Muqtadir, S. Suryono, and V. Gunawan, “The Implementation of
Grey Forecasting Model for Forecast Result’s Food Crop Agricultural,” Sci. J. Informatics, vol. 3, no. 2, pp. 159–166, 2016, doi: 10.15294/sji.v3i2.7912.
-
[19] I. Sidiq, E. Febianti, and P. F. Ferdinant, “Peramalan Kebutuhan
Konsumsi Listrik Menggunakan Grey Prediction Model,” J. Tek. Ind., vol. 1, no. 1, pp. 1–6, 2013, [Online]. Available:
http://jurnal.untirta.ac.id/index.php/jti/article/view/109.
-
[20] I. N. Z. S. M. Nurfitri Imro’ah, “Peramalan Harga Emas Batangan
Menggunakan Metode Grey Double Exponential Smoothing,” Bimaster Bul. Ilm. Mat. Stat. dan Ter., vol. 9, no. 4, pp. 497–504, 2020, doi: 10.26418/bbimst.v9i4.42280.
-
[21] G. F. Fitri, F. Agustina, and R. Marwati, “Penerapan Metode Grey
System Pada Peramalan Produk Olefins (Studi Kasus PT. Chandra Asri Petrochemical Tbk),” EurekaMatika, vol. 6, no. 2, pp. 52–63, 2018.
-
[22] A. Fitro, Rudianto, and H. Prasetyo, “Implementasi Metode Grey
Verhulst Untuk Mendukung Kebijakan Dalam Mengantisipasi Mahasiswa Dropout,” vol. 3, no. 02, pp. 180–187, 2021.
-
[23] L. D. Immawan and A. Ahdika, “Comparison of Grey-Markov (1,1),
Grey-Markov (2,1), and moving average methods in forecasting small sized data of the unit price of materials in batam,” AIP Conf. Proc., vol. 2021, no. 2018, 2018, doi: 10.1063/1.5062783.
-
[24] N. L. Nariswari and C. N. Rosyidi, “Aplikasi Metode Grey
Forecasting Pada Peramalan Kebutuhan Bahan Bakar Alternatif Ramah Lingkungan di PT. Indocement Tunggal Prakarsa Tbk,” PERFORMA, vol. 14, no. 2, pp. 99–106, 2015, doi:
10.20961/performa.14.2.10986.
-
[25] D. R. Darmawanti, Yundari, and N. M. Huda, “Prediksi Realisasi
Penerimaan Pajak Bumi Dan Bangunan Provinsi Kalimantan Barat Dengan Model Grey-Markov(1, 1),” Bul. Ilm. Math. Stat dan Ter., vol. 11, no. 3, pp. 503–512, 2022.
-
[26] B. H. S. Atma and S. Sugiyarto, “Adaptive neuro fuzzy inference
-
system untuk peramalan jumlah wisatawan,” J. Ilm. Mat., vol. 7, no. 1, p. 1, 2020, doi: 10.26555/konvergensi.v7i1.19195.
-
[27] I. G. B. Ngurah Diksa, “Peramalan Gelombang Covid 19
Menggunakan Hybrid Nonlinear Regression Logistic – Double Exponential Smoothing di Indonesia dan Prancis,” Jambura J. Math., vol. 3, no. 1, pp. 37–51, 2021, doi: 10.34312/jjom.v3i1.7771.
-
[28] H. W. Tresnani, A. Sihabuddin, and K. Mustofa, “Optimasi
Parameter Pada Metode Peramalan Grey Holt - Winter Exponential Smoothing Dengan Golden Section,” Berk. MIPA, vol. 25, no. 3, pp. 312–325, 2018.
-
[29] D. I. Purnama and O. P. Hendarsin, “Peramalan Jumlah Penumpang
Berangkat Melalui Transportasi Udara di Sulawesi Tengah Menggunakan Support Vector Regression (SVR),” Jambura J. Math., vol. 2, no. 2, pp. 49–59, 2020, doi: 10.34312/jjom.v2i2.4458.
-
[30] D. N. Adli, “Prediksi Harga Jagung Menggunakan Metode Fuzzy
Time Series Dengan Atau Tanpa Menggunakan Markov Chain,” J. Nutr. Ternak Trop., vol. 4, no. 1, pp. 49–54, 2021, doi:
10.21776/ub.jnt.2021.004.01.6.
-
[31] R. Assakhiy, S. Anwar, and F. Ar, “Peramalan Realisasi Penerimaan
Zakat Pada Baitulmal Aceh Dengan Mempertimbangkan Efek Dari Variasi Kalender,” J. Ekon. dan Pembang., vol. 27, no. 2, pp. 27–45, 2019.
-
[32] L. H. Zulkieflimansyah, Muhammad Nurjihadi, Diah Anggeraini
Hasri, Nova Adhitya Ananda, “Proyeksi Dinamika Pendapatan Asli Daerah Nusa Tenggara Barat,” J. Maneksi, vol. 10, no. 2, pp. 231– 245, 2021.
-
[33] G. B. Nabilah, Y. N. Nasution, and I. Purnamasari, “Peramalan
Indeks Harga Konsumen Provinsi Kalimantan Timur dengan Metode Grey Double Exponential Smoothing Holt,” Pros. Semin. Nas. Mat. Stat. dan Apl., vol. Mei, no. II, pp. 69–80, 2022.
-
[34] I. G. D. A. L K Widyapratiwi, I P A Mertasana, “Peramalan Beban
Listrik Jangka Pendek Di Bali Menggunakan Pendekatan Adaptive Neuro-Fuzzy Inference System (Anfis),” Maj. Ilm. Teknol. Elektro, vol. 11, no. 2, 2013.

[HALAMAN INI SENGAJA DI KOSONGKAN]
ISSN 1693 – 2951
Anom Manuaba: Analisis Peramalan Penerimaan Negara …
Discussion and feedback