Identifikasi Sistem Motor DC dan Kendali Linear Quadratic Regulator Berbasis Arduino-Simulink Matlab
on
Majalah Ilmiah Teknologi Elektro, Vol. 17, No. 2,Mei - Agustus 2018
DOI: https://doi.org/10.24843/MITE.2018.v17i02.P20
299
Identifikasi Sistem Motor DC dan Kendali Linear Quadratic Regulator Berbasis Arduino-Simulink Matlab
Fahmizal1, Fahmy Fathuddin2, Rudi Susanto3
Abstract— This paper describes the identification process of DC motor system with the experimental technique using indetification tool in Matlab. After the DC motor model system is obtained, the optimal control technique in this case using linear quadratic regulator (LQR) is used to view the system response step. In this paper, the DC motor identification module with Arduino DC was developed to facilitate in terms of getting the model of DC motor by approaching first and second order models. This module is integrated between Arduino and Simulink Matlab which is used as input-output data acquisition. The results of the system identification process in the form of DC Motor model with modeling auto regressive exogenous (ARX) second order. Furthermore, the application of LQR control technique with parameters of Q element matrix is sought by multiplication of transpose Matrix C system with Matrix C of the system. While the R element matrix in tuning experimentally with value 0.000001. From the test results obtained that LQR control produces a more optimal system response time constant when compared with PID control of 0.02 seconds.
Intisari— Makalah ini memaparkan proses identifikasi sistem Motor DC dengan teknik eksperimen menggunakan sistem indetifikasi tool pada Matlab. Setelah sistem model Motor DC diperoleh, teknik kendali optimal dalam hal ini menggunakan linear quadratic regulator (LQR) digunakan untuk melihat step respon sistem. Pada penelitian ini, modul identifikasi sistem Motor DC dengan Arduino dikembangkan untuk memudahkan dalam hal mendapatkan model Motor DC dengan cara pendekatan model orde satu dan dua. Modul ini terintegrasi antara Arduino dengan Simulink Matlab yang digunakan sebagai akusisi data input - output. Hasil dari proses identfikasi sistem berupa model Motor DC dengan pemodelan auto regressive exogenous (ARX) orde dua. Selanjutnya penerapan teknik kendali LQR dengan parameter Matriks elemen Q dicari dengan cara perkalian antara transpose Matriks C sistem dengan Matriks C sistem tersebut. Sedangkan Matriks elemen R di tuning secara eksperimen dengan nilai 0.000001. Dari hasil pengujian diperoleh bahwa kendali LQR menghasilkan konstanta waktu respon sistem lebih optimal bila dibandingkan dengan kendali PID sebesar 0.02 detik.
Kata Kunci— Identifikasi sistem, Motor DC , LQR.
-
1Dosen, Departemen Teknik Elektro dan Informatika, Sekolah Vokasi, Universitas Gadjah Mada, Sekip Unit III, Gd. Herman Yohanes, Yogyakarta 55281, Telp: (0274) 561111; Fax.: (0274) 542908, e-mail: fahmizal@ugm.ac.id
-
2,3Staff Kependidikan, Departemen Teknik Elektro dan Informatika, Sekolah Vokasi, Universitas Gadjah Mada, Sekip Unit III, Gd. Herman Yohanes, Yogyakarta 55281, Telp: (0274) 561111; Fax.: (0274) 542908, e-mail: fahmy.fathuddin@ugm.ac.id ; rudi.susanto@ugm.ac.id
Fahmizal: Identifikasi Sistem Motor DC dan Kendali Linear ...
Untuk mengetahui dan mempelajari suatu sifat pada sistem diperlukan identifikasi sistem, hal ini diperoleh dengan cara memodelkannya secara matematika berdasarkan sifat-sifat komponennya [1]. Dari hasil identifikasi ini diperoleh transfer function. Dengan model transfer function ini, dapat diketahui sifat respon sistem terhadap berbagai input. Berdasarkan pengetahuan atas sifat sistem tersebut, dapat ditentukan tindakan atau perlakuan yang tepat agar sistem berperilaku sesuai yang diinginkan. Identifikasi sistem merupakan suatu pendekatan eksperimental untuk menentukan model dinamik dari suatu sistem.
Secara mendasar sebuah model dibangun dari data yang diamati [2]. Identifikasi suatu sistem merupakan tugas penting dalam penelitian ilmiah sebagai langkah pertama dari setiap analisis sistem [3]. Namun, untuk mendapatkan model diperlukan prosedur yang tidak mudah. Terdapat dua cara dalam hal memperoleh model matematis dari sebuah sistem fisik, yaitu melalui pendekatan analisis dan ekperimen.
Ada beberapa teknik dalam hal mendapatkan model suatu sistem Motor DC dengan cara eksperimen. Salah satu diantaranya adalah dengan cara mengamati data masukan dan keluaran dari Motor DC tersebut [4]. Namun ada juga peneliti yang mengguanakan algoritma kecerdaran buatan seperti recurrent neural networks (RNN), metode yang digunakan dengan jaringan syaraf tiruan, dimana model dinamik Motor DC diperoleh dari nilai minimum kesalahan hasil learning dari suatu model Motor DC yang telah diketahui parameternya [5]. Selanjutnya, penelitian pada [6] memanfaatkan tegangan balik pada Motor DC untuk dijadikan variabel masukan dan kecepatan putar Motor DC sebagai variabel keluaran. Hubungan antara masukan dan keluaran dievaluasi dengan sistem identifikasi tool yang terdapat pada Matlab.
Motor DC bekerja secara nonlinear terutama saat terjadi diberi variasi beban. Pengendali konvensional, seperti PID kontroller [7–9] sangat umum digunakan karena memiliki performa yang baik dalam mengendalikan sistem linear [10]. Pada [11] memaparkan sistem pengendalian motor induksi menggunakan kontroler PID dengan metode field oriented control (FOC). Metode ini digunakan untuk memperbaiki sinyal kontrol arus torsi di dalam sistem kontroler PID. Selain itu, teknik kendali optimal telah digunakan oleh beberapa peneliti seperti menggunakan linear quadratic regulator (LQR) [12–13].
Pada makalah ini digunakan Motor DC dengan magnet permanen sebagai plant yang akan diidentifikasi serta dikendalikan dengan dengan teknik kendali optimal LQR. Penelitian ini menggunakan identifikasi black box [14], yaitu dengan mengamati input – ouput dari suatu sistem Motor DC. Pada penelitian ini juga dikembangkan modul identifikasi
p-ISSN:1693 – 2951; e-ISSN: 2503-2372

Motor DC dengan menggunakan Arduino dan terintegrasi dengan Simulink-Matlab.
-
A. Metode Identifikasi
Dalam sistem kendali, identifikasi sistem pada umumnya dapat digambarkan seperti pada Gambar 1. Langkah-langkah proses identifikasi sistem terdiri atas empat tahap, yaitu [4]:
-
a) . Tersedianya data input-output plant yang akan diidentifikasi.
-
b) . Pemilihan struktur model.
-
c) . Estimasi parameter-parameter model.
-
d) . Validasi model yang telah diidentifikasi (struktur dan nilai parameter-parameternya).
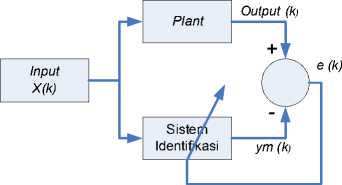
Gambar 1. Blok diagram proses identifikasi suatu sistem.
Pada penelitian ini proses identifikasi motor DC dilakukan secara open loop melalui Arduino dan personal computer (PC) dengan terhubung Simulink-Matlab. Metode yang digunakan untuk identifikasi adalah metode identifikasi statis. Identifikasi statis salah satu yang paling banyak digunakan adalah dengan metode open loop dengan masukkan step seperti yang disajikan pada Gambar 2.
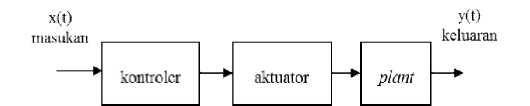
Gambar 2. Diagram blok identifikasi plant dengan metode open loop
-
B. Karakteristik Sistem
Karakterisitik sistem merupakan ciri khusus perilaku dinamik suatu sistem atau dinamakan dengan istilah spesifikasi performansi sistem. Tanggapan (respon) keluaran sistem muncul akibat diberikannya suatu sinyal masukan atau setelah diberi sinyal uji. Berdasarkan karakteristik respon sistem dapat diklasifikasikan menjadik karakteristik respon waktu (time respons) dan karakteristik respon frekuensi (frequency respons). Lebih jauh, pada penelitian ini diamati karakteristik respon waktu dari Motor DC. Tujuan dari pengamatan karakterisktik respon waktu ialah untuk mengamati bentuk respon keluaran sistem terhadap berubahnya waktu. Secara umum spesifikasi perfomansi respon waktu dapat dibagi atas dua tahapan pengamatan, yaitu spesifikasi respon transien dan respon steady state. Lebih jauh, pengamatan karakteristik suatu sistem dapat didekati pada sistem orde satu dan orde dua.
-
1) Sistem Orde Satu
Spesifikasi respon dengan sinyal masukan step pada sistem orde satu dapat dinyatakan dalam dua macam spesifikasi yaitu: spesifikasi respon transien dan spesifikasi respons steady state. Grafik respon sistem orde satu untuk Xzz = 1 dan Yss = K disajikan pada Gambar 3.
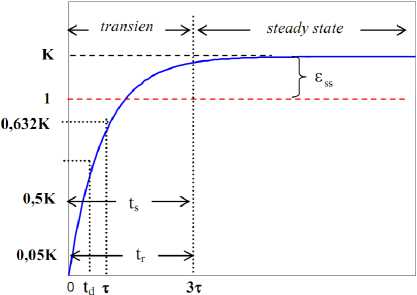
Gambar 3. Respon orde satu terhadap masukan units step.
-
2) Sistem Orde Dua
Persamaan umum sistem orde dua dinyatakan dalam Persamaan (1).
C (s) = Kω (1)
R (s) s2 + 2ξωns + ω1n
Dimana, K adalah gain overall, ξ adalah rasio redaman dan ω adalah frekuensi alami. Bentuk umum kurva respon orde dua untuk masukan sinyal unit step ditunjukkan oleh Gambar 4.
Gambar 4. Respon orde dua terhadap masukan units step.
-
C. Model Matematis Motor DC
Pengaturan kecepatan pada Motor DC dengan penguatan medan dengan menggunakan magnet permanen ini dapat dilakukan dengan mengatur tegangan pada kumparan jangkar [17]. Karena medan magnet yang dihasilkan berasal dari magnet permanen maka kuat medan magnet tersebut bernilai tetap. Skema rangkaian Motor DC dapat dilihat pada Gambar 5.
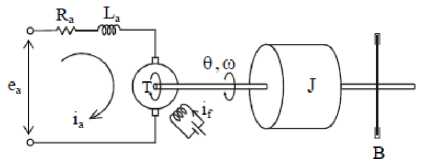
Gambar 5. Diagram skematik Motor DC.
Untuk keperluan identifikasi model motor DC berdasarkan analitik maka transfer function sistem diperoleh seperti yang diuraikan pada Gambar 6.
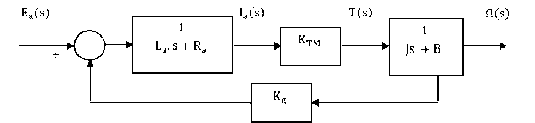
Gambar 6. Diagram blok dari persamaan model Motor DC.
Ω (s)
Fungsi alih loop tertutup dapat diperoleh
Ea (S)
dari
Persamaan (2).
KTM
Ω(s) (La s+Ra)(Js+B)
Ea (s) 1+ KTM.Kg.s
(La s+Ra)(Js+B)
Ω(s) __________KTM__________
Ea (s) (La s+Ra)(Js+B)+‰Kg)
Ω(s) _______________KTM_______________
Ea (S) J La s2 +(B La + J Ra) s+(Ra B+Ktm Kg)
Secara umum nilai induktansi dari kumparan jangkar motor La sangatlah kecil sehingga nilainya dapat diabaikan,
sehingga Persamaan (2) menjadi Persamaan (3).
Ω(s) _______KTM_______
Ea (s) (J Ra) s+Ra B+Ktm Kg
(3)
-
D. Kendali Optimal Linear Quadratic Regulator (LQR)
LQR adalah sebuah kendali optimal yang bertujuan membawa state akhir ke titik nol dengan meminimalkan cost fuction. Jenis kendali ini bertujuan mencari nilai gain state feedback (K) [16]. Misalkan sebuah plant mempunyai bentuk state space pada Persamaan (4).
X_ Ax + Bu y_ Cx ( )
dengan indeks performansi pada Persamaan (5).
1T
J _ 2 ∫ {xT(tQX(t^ + uT(t^Ru(t)}dt (5)
t0
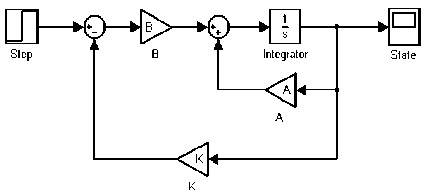
Blok diagram yang menunjukan konfigurasi LQR di tunjukan oleh Gambar 7.
-
Gambar 7. Diagram blok LQR.
Dalam mencari nilai gain state feedback (K), pada Matlab bisa dilakukan langsung dengan sintaks: “[K,S,E]=lqr(A,B,Q,R)”. Dengan K adalah gain state feedback, S adalah solusi persamaan Riccati dan E adalah closed-loop eigenvalue.
-
III. Identifikasi Sistem Motor DC
A. Perancangan Sistem Akusisi Data
Penelitian ini merancang sistem modul mikrontroller berbasis Arduino sebagai data akusisi dan data proses yang dijelaskan pada Gambar 8.
(2)
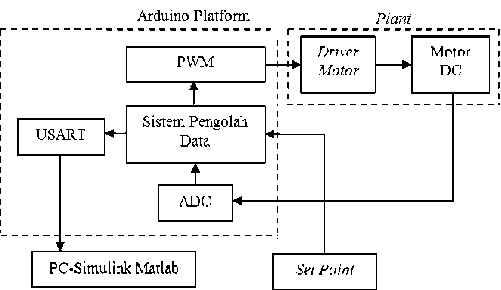
Gambar 8. Diagram blok rancangan sistem akusisi data dengan Arduino.
Setelah proses identifikasi model motor DC diperoleh, tahapan selanjutnya adalah sistem kendali kecepatan motor DC yang digambarkan dalam diagram blok pada Gambar 9.
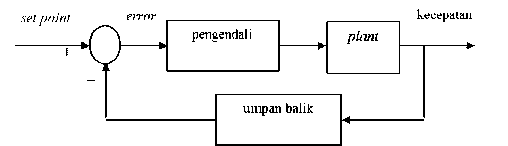
Gambar 9. Diagram loop tertutup kendali kecepatan Motor DC.
B. System Identification (SID) pada Matlab
System Identification (SID) merupakan tool tambahan dari perangkat lunak Matlab (Mathworks Inc.). SID dapat digunakan sebagai sarana identifikasi yang dijelaskan pada Gambar 10, simulasi dan analisis dari sistem dinamik dengan menggunakan graphical user interface (GUI).
Fahmizal: Identifikasi Sistem Motor DC dan Kendali Linear ...
p-ISSN:1693 – 2951; e-ISSN: 2503-2372

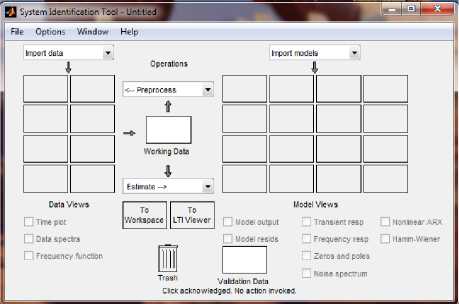
Gambar 10. System identification tool pada Matlab.
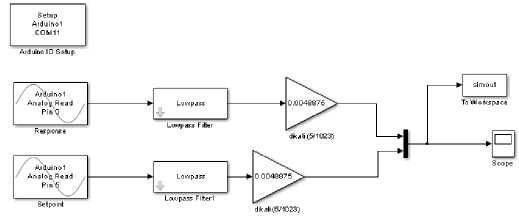
Gambar 12. Blok Simulink untuk akuisisi data.
Pada penelitian ini, telah berhasil mewujudkan sebuah modul identifikasi dan kendali Motor DC berbasis Arduino (Gambar 11). Modul ini dapat terintegrasi dengan Simulink. Dengan capaian ini, peneliti dapat melakukan proses identifikasi sistem Motor DC dan data identifikasi ini seterusnya akan digunakan sebagai acuan model matematis dari Motor DC. Gambar 12 menjelaskan blok Simulink untuk akuisisi data, Gambar 13 menjelaskan identifikasi sistem Motor DC dengan toolbox dan Gambar 14 menjelaskan proses verifikasi dan validasi transfer function dengan respon plant. Berikut Tabel 1 hasil identifikasi dengan pendekatan dua tipe pendekatan.
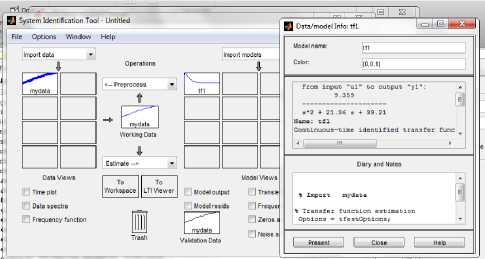
Gambar 13. Identifikasi sistem dengan SID.
Tabel 1. Hasil Pendekatan Model Motor DC.
|
Pendekatan orde 1 |
0.4748 s+1.989 |
|
Pendekatan orde 2 |
9.359 s2 +21.36s+39.21 |
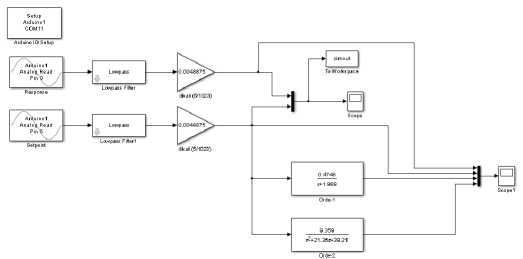
Gambar 14. Verifikasi dan validasi transfer function dengan respon plant.

Gambar 11. Perangkat modul identifikasi dan kendali Motor DC berbasis Arduino terintegrasi dengan Simulink.
Sebelum menggunakan kendali optimal LQR maka terlebih dahulu mengalisis open loop sistem dalam bentuk transfer function lalu diubah kedalam model state space. Berikut ini pengujian dan pembahasan hasil identifikasi Motor DC dengan dua tipe pendekatan, yaitu orde satu dan orde dua. Dengan memberikan sinyal masukan step terlihat pada Gambar 15 dan Gambat 16 bahwa hasil pendekatan orde satu dan orde dua tidak jauh berbeda.
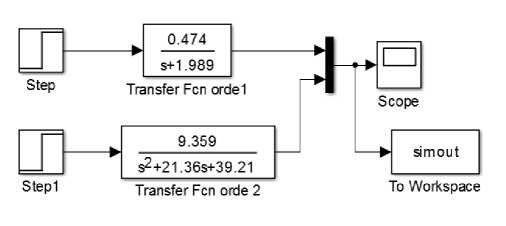
Gambar 15. Simulink respon sinyal step pada sistem orde satu dan orde dua.
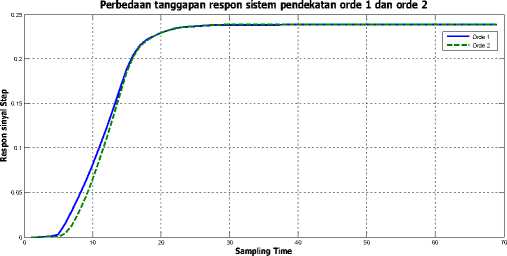
gambar 16. perbedaan tanggapan respon sistem pendekatan orde 1 dan orde 2.
Langkah selanjutnya dengan menggunakan Matlab, mengubah model dari bentuk transfer function kedalam bentuk state space dengan menggunakan perintah “[A,B,C,D] = tf2ss(num,den)”. Hasil dari konversi ke dalam bentuk state space di jelaskan pada Tabel 2.
Tabel 2. Hasil dari Konversi kedalam Bentuk State Space.
|
Transfer function model pendekatan Motor DC |
Model dalam bentuk State Space |
|
0.474 |
A = -1.989 |
|
s +1.989 |
B = 1 |
|
C = 0.4780 | |
|
Pendekatan orde 1 |
D = 0 |
|
Γ - 21.36 - 39.211 | |
|
A = | |
|
9.359 |
L 1 o J |
|
s 2 + 21.36 s + 39.21 |
1 B = |
|
L o J | |
|
C = [0 9.359 ] | |
|
Pendekatan orde 2 | |
|
D = 0 |
Simulink blok pemodelan dalam bentuk state space sistem disajikan pada Gambar 17 yang mengacu pada Tabel 2.
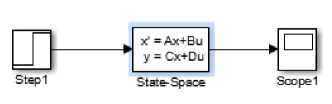
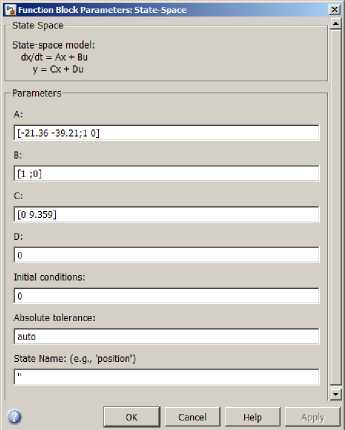
Gambar 17. Simulink blok pemodelan dalam bentuk state space.
Selanjutnya dilakukan analisis dengan memeriksa controllability dan observability yang dijelaskan pada Tabel 3. Controllability adalah suatu pemeriksaan dimana suatu sistem dikatakan terkendali apabila jika Matriks elemen controllability (ctr) yang dijelaskan pada Persamaan (6) yang berukuran n x n memiliki rank dengan nilai n. Atau jika determinan dari Matriks controllability adalah tidak lah nol [18].
ctr =[B AB ... An-1BJ (6)
Dan observability adalah ukuran seberapa baik keadaan internal suatu sistem dapat disimpulkan dari pengetahuan tentang output eksternalnya. Matriks elemen observability (obsr) dijelaskan pada Persamaan (7).
obsr=C AC ... A-1CT (7)
Dengan menggunakan perintah pada Matlab, controllability dan observability dapat diperoleh dengan perintah berikut, rank(ctrb(A,B))dan rank(obsv(A,C). Bila telah memenuhi syarat maka dilanjutkan dengan memberi nilai Matriks Q dan R untuk mendapatkan elemen Matriks K dengan menggunakan LQR.
Fahmizal: Identifikasi Sistem Motor DC dan Kendali Linear ...
Tabel 3. Rank Controllability dan Observability dari Model Sistem.
|
Model pendekatan Motor DC |
Controllability |
Observability |
|
A = -1.989 B = 1 C = 0.4780 D = 0 |
1 |
1 |
p-ISSN:1693 – 2951; e-ISSN: 2503-2372
|
Pendekatan orde 1 | |||
|
A= B= C = D = Pende |
■-21.36 - 39.21’ 1 0 f11 L o J ’ 0 9.359 ] 0 katan orde 2 |
2 |
2 |
Dari hasil rank controllability dan observability disimpulkan bahwa sistem dapat dikendalikan dan teramati. Maka selanjutnya mencari elemen Matriks K dengan LQR. Elemen Matriks K ini dapat diperoleh dengan menjalankan perintah berikut pada Matlab “[K,S,E]=lqr(A,B,Q,R)” dimana S adalah solusi persamaan Riccati dan E adalah closed-loop eigenvalue. Dari hasil perintah tersebut, diperoleh Matriks elemen K pada masing-masing model dijelaskan pada Tabel 4. Percobaan pertama dengan memberikan nilai Matriks elemen Q = transpose(C)*C dan R = 0.000001.
Tabel 4. Matriks elemen K pada masing-masing model dengan LQR.
|
Model dalam bentuk State Space |
Matriks elemen K dengan teknik LQR | |
|
A = -1.989 B = 1 C = 0.4780 D = 0 |
K = 472.0152 | |
|
A = B = C = D = |
Γ-21.36 - 39.21 L 1 0 Γ11 L 0 J '0 9.359 ] 0 |
116.8 K = 9319.9 |
Berikut Tabel 5 adalah listing program pada m-file Matlab untuk mencari elemen Matriks K pada pendekatan model orde dua dengan menggunakan LQR. Model motor DC orde dua ini telah di validasi seperti yang disajikan pada Tabel 1. Gambar 18 dan Gambar 19 adalah grafik respon sistem hasil dari ploting perintah m-file Matlab pada Tabel 5.
Tabel 5. Listing program pada m-file Matlab untuk mencari elemen Matriks K dengan teknik LQR.
%transfer function sistem pendekatan orde dua
num2 = 9.359;
den2= [1 21.36 39.21];
G=tf(num2,den2)
%step respons sistem pendekatan orde dua
figure(1)
step(G)
%konversi kedalam model state space
[A,B,C,D] = tf2ss(num2,den2);
modelMotor=ss(A,B,C,D);
modelMotor=tf(modelMotor)
%pembobotan Matriks Q dan R
R=0.000001;
Q=transpose(C)*C;
%mencari element Matriks K dengan LQR
K=lqr(A,B,Q,R)
sys=ss(A,B,C,D);
Af=A-B*K;
T=ss(Af,B,C,D);
T=tf(T)
%step respons sistem setelah umpan balik
Matriks K dengan LQR
figure(3)
step(T)
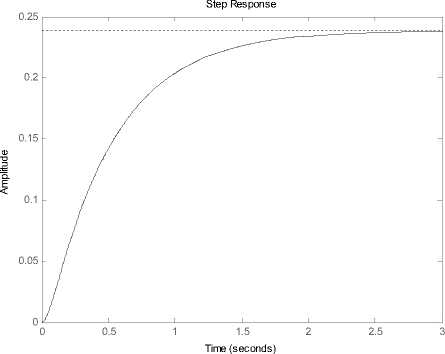
Gambar 18. Step respon sistem Motor DC pendekatan orde dua.
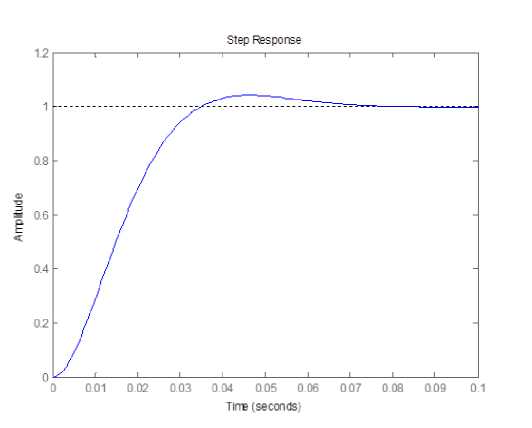
Gambar 19. Step respon sistem Motor DC pendekatan orde dua setelah umpan balik Matriks K dengan LQR.
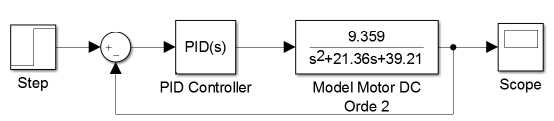
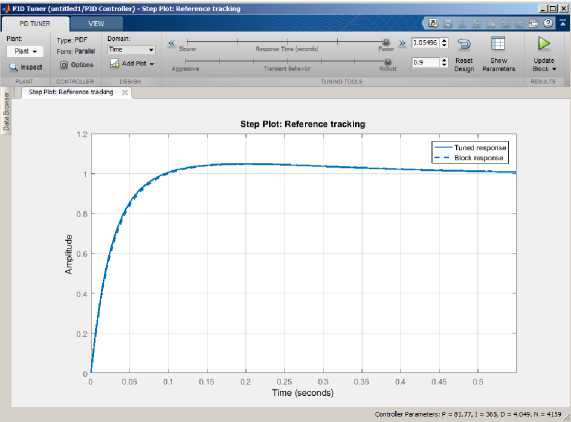
Gambar 20. Step respon sistem dengan kendali PID pada sistem pendekatan orde dua dengan parameter Kp = 81.76 , Ki = 364.98 dan Kd = 4.04.
Dari hasil respon sinyal dapat diperhatikan bahwa pada Gambar 18 adalah step respon sistem pendekatan orde dua tanpa umpan balik atau dalam kondisi open loop. Saat diberi sinyal masukan step, respon dari sistem belum mampu menuju keadaan steady state dengan sinyal masukan berupa fungsi step. Pada Gambar 16, saat sistem dalam kondisi close loop menggunakan kendali LQR dengan nilai k1 = 116.8 dan k2 = 9319.9diperoleh respon konstanta waktu (τ) saat respon mencapai 63,2% dari respon steady state dengan waktu sekitar 0.03 detik. Bila dibandingkan dengan kendali PID dengan parameter konstanta proporsional senilai 81.76, integral senilai 364.98 dan differensial senilai 4.04 seperti yang disajikan pada Gambar 20 diperoleh waktu sekitar 0.05 detik. Itu artinya respon kendali LQR lebih optimal sebesar 0.02 detik.
Teknik kendali optimal yang dibahas pada makalah ini adalah dengan LQR, dimana Matriks elemen Q dicari dengan cara perkalian antara transpose Matriks C sistem dengan Matriks C sistem tersebut. Sedangkan Matriks elemen R di tuning secara eksperimen dengan nilai 0.000001. Dari hasil pengujian penerapan sistem kendali LQR dapat disimpulkan bahwa kendali LQR menghasilkan respon konstanta waktu (τ) yang lebih optimal bila dibandingkan dengan kendali PID sebesar 0.02 detik.
Ucapan Terima Kasih
Penulis mengucapkan terima kasih kepada Departemen Teknik Elektro dan Informatika Sekolah Vokasi Universitas Gadjah Mada atas dukungan yang telah diberikan kepada penulis.
Referensi
-
[1] Wang X, Yin T, Chen J, et al. Rapid design of Motor DC speed control system based on Matlab[J]. Applied Mechanics & Materials, 2015, 743:168-171.
-
[2] L. Ljung, “Prediction error estimation methods”, Circ. Syst. Signal Process. 21 (2002) 11–21.
-
[3] G. H. Shakouri and H. R. Radmanesh, “Identification of a continuous time nonlinear state space model for the extenal power system dynamic equivalent by neural network,” Electrical Power and Energy Systems, vol. 31, pp. 334-344, 2009.
-
[4] Tang, Wei-Jie, Zhen-Tao Liu, and Qian Wang. "Motor DC speed control based on system identification and PID auto tuning." Control Conference (CCC), 2017 36th Chinese. IEEE, 2017.
-
[5] Ismeal, Godem A., Karol Kyslan, and Viliam Fedák. "Motor DC identification based on Recurrent Neural Networks." Mechatronics-Mechatronika (ME), 2014 16th International Conference on. IEEE, 2014.
-
[6] Kamdar, Sauyma, Harsidh Brahmbhatt, Tigmanshu Patel, and Manish Thakker. "Sensorless speed control of high speed brushed Motor DC by model identification and validation." In Engineering (NUiCONE), 2015 5th Nirma University International Conference on, pp. 1-6. IEEE, 2015.
-
[7] Wang, Jun-Sheng, and Guang-Hong Yang. "Data-Driven OutputFeedback Fault-Tolerant Compensation Control for Digital PID Control Systems With Unknown Dynamics." IEEE Transactions on Industrial Electronics 63, no. 11 (2016): 7029-7039.
-
[8] Viola, J., L. Angel, and J. M. Sebastian. "Design and robust performance evaluation of a fractional order PID controller applied to a Motor DC ." IEEE/CAA Journal of Automatica Sinica 4, no. 2 (2017): 304-314.
-
[9] Shanmugasundram, R., K. Muhammad Zakariah, and N. Yadaiah. "Implementation and performance analysis of digital controllers for brushless Motor DC drives." IEEE/ASME transactions on mechatronics 19, no. 1 (2014): 213-224.
-
[10] G. Ellis, Control system design guide : a practical guide. 3rd ed 2004, Amsterdam ; Boston: Elsevier Academic Press.
-
[11] Raka Ardana, I Wayan. Simulasi Sistem Kontroler Pid Untuk Motor Induksi Menggunakan Perangkat Lunak Matlab / Simulink. Majalah Ilmiah Teknologi Elektro, vol. 7, no. 2, May, 2013.
-
[12] Haron, Hartini Sharninayati. "Linear quadratic regulator (LQR) controller design for DC servo motor." PhD diss., Universiti Tun Hussein Onn Malaysia, 2013.
-
[13] Srivastava, Saurabh, and V. S. Pandit. "A scheme to control the speed of a Motor DC with time delay using LQR-PID controller." In Industrial Instrumentation and Control (ICIC), 2015 International Conference on, pp. 294-299. IEEE, 2015.
-
[14] L. Ljung, System Identification Theory for the User, 2nd ed., Prentice Hall, CA: Linkoping University Sweden, 1999.
-
[15] L. A. Zadeh, “On the Identification Problem,” IEEE Transactions On Circuit Theory, vol. 3, no 4, pp.277-281.1956.
-
[16] Yu, Gwo-Ruey, and Rey-Chue Hwang. "Optimal PID speed control of brush less Motor DC s using LQR approach." Systems, Man and Cybernetics, 2004 IEEE International Conference on. Vol. 1. IEEE, 2004.
-
[17] Peng, Jinzhu, and Rickey Dubay. "Identification and adaptive neural network control of a Motor DC system with dead-zone characteristics." ISA transactions 50.4 (2011): 588-598.
-
[18] Ogata, Katsuhiko. Modern Control Engineering Third Edition. New Jersey, Prentice Hall, Upper Saddle River. 1997.
Fahmizal: Identifikasi Sistem Motor DC dan Kendali Linear ...
p-ISSN:1693 – 2951; e-ISSN: 2503-2372

{Halaman ini sengaja dikosongkan}
ISSN 1693 – 2951; e-ISSN: 2503-2372
Fahmizal: Identifikasi Sistem Motor DC dan Kendali Linear ...
Discussion and feedback