Implementasi Fuzzy Logic dan Algoritma Genetika dalam Pembebanan Ekonomis pada Sistem Pembangkitan di Bali
on
Teknologi Elektro, Vol. 16, No. 3,September - Desember 2017
99
Implementasi Fuzzy Logic dan Algoritma Genetika dalam Pembebanan Ekonomis pada Sistem Pembangkitan di Bali
Nasrul Faisal1, Rukmi Sari Hartati2, I Wayan Sukerayasa3
Abstract—Implementation of fuzzy logic and genetic algorithms on the generation system in Bali is aims to minimize the cost of the system in Bali. Every hour there will always be changes in the load in order to obtain the minimum total operating costs by taking into account the limits of technical and operational, namely the maximum and minimum power generated every unit of generator. The operation of the plant is economically affected by the load to be supplied, the maximum limit and the minimum output power plants, as well as the cost of fuel to operate. In this research, optimization studies with fuzzy logic and genetic algorithms in loading economical in Bali ignoring transmission losses using Matlab software. Using data of 9 unitsgenerator in Bali on May 18, 2014 showed that the cost can be reduced by 21.202% more efficient when compared to the existing.
Intisari—Implementasi fuzzy logic dan algoritma genetika pada sistem pembangkitan di Bali ini bertujuan untuk meminimumkan biaya pada sistem di Bali. Setiap jam akan selalu terjadi perubahan beban sehingga diperoleh total biaya operasi yang minimum dengan tetap memperhatikan batas-batas teknis dan operasional yaitu batas maksimum dan minimum daya yang dibangkitkan setiap unit generator. Pengoperasian pembangkit secara ekonomis dipengaruhi oleh beban yang akan disuplai, batas maksimun dan minimum daya output pembangkit, serta biaya bahan bakar untuk mengoperasikan. Dalam penelitian ini dilakukan studi optimasi dengan metode fuzzy logic dan algoritma genetika dalam pembebanan ekonomis pada sistem 150 kV Bali dengan mengabaikan rugi-rugi transmisi menggunakan perangkat lunak Matlab. Dengan menggunakan data 9 unit pembangkitan di Bali pada tanggal 18 Mei 2014 didapatkan hasil bahwa biaya yang dapat ditekan sebesar 21,202% lebih efisien bila dibandingkan dengan kondisi eksiting.
Kata kunci –- Penjadwalan Ekonomis, Fuzzy Logic, Algoritma Genetika
-
I. PENDAHULUAN
Bali saat ini sedang mengalami pertumbuhan hunian dan pertumbuhan industri pariwisata seperti hotel, villa, restaurant hingga tempat wisata penunjang lainnya. Dengan pertumbuhan yang sangat pesat ini, maka akan diikuti dengan pertumbuhan pemakaian energi listrik yang besar pula.
Energi listrik tidak dapat disimpan dalam jumlah banyak sehingga harus tersedia pada saat dibutuhkan oleh konsumen, akibatnya timbul persoalan dalam menghadapi kebutuhan daya listrik yang berubah dari waktu ke waktu. Kelistrikan di Bali saat ini dipasok oleh beberapa pembangkit, yaitu pembangkit yang berlokasi di Pesanggaran, Celukan Bawang, Gilimanuk, dan Pemaron. Total daya yang terpasang di Bali saat ini sebesar 958,72 MW serta 340 MW yang disalurkan dari Jawa melalui sistem interkoneksi kabel bawah laut [1].
Pasokan daya yang ada di Bali saat ini dipandang cukup apabila salah satu pembangkit tidak beroperasi pada saat dilakukan pemeliharaan, namun tidak menutup kemungkinan bisa terjadi kekurangan pasokan daya yang dapat mengakibatkan terjadinya pemadaman bergilir [2]. Maka dari itu perlu diambil langkah untuk memenuhi kebutuhan listrik baik secara kualitas maupun kuantitas dari sisi permintaan (demand side management) dan dari sisi penyedia (supply side management). Penghematan biaya operasi terutama penghematan biaya bahan bakar sistem di Bali juga tidak kalah pentingnya untuk dilakukan. Salah satu bagian pengoperasian sistem tenaga listrik yang mengarah ke hal ini adalah pengalokasian pembebanan optimal (economic dispatch) pada pembangkitan. Cara ini dilakukan untuk meminimumkan biaya operasi pada sistem tenaga listrik dengan cara mengoptimalkan pengalokasian pembangkitan daya yang beroperasi pada sistem Bali.
Terkait dengan optimasi pembebanan ekonomis, telah dilakukan beberapa penelitian sebelumnya. Penelitian yang dilakukan oleh Rumana (2011) dengan judul Implementasi Algoritma Genetik dalam Economic Dispatch dengan Valve Point Loading [3]. Penelitian ini membahas suatu metode yang menggunakan algoritma genetik untuk penyelesaian masalah economic dispatch dengan model permasalahannya adalah unit-unit pembangkit dengan banyak katup (multivalve generating units) yang memiliki fungsi biaya non-convex. Penggunaan algoritma genetika berhasil menyelesaikan permasalahan economic dispatch dengan fungsi biaya non-convex tersebut bila dibandingkan dengan metode LaGrange. Disisi lain penggunaan metode kecerdasan buatan juga diterapkan untuk mencari operasi ekonomis pembangkit thermal sistem 500kV Jawa – Bali dengan pendekatan algoritma Fuzzy Logic [4]. Hasil penelitian tersebut apabila dibandingkan dengan data eksisting sistem, maka penjadwalan unit pembangkit dengan pendekatan algoritma fuzzy logic memberikan hasil 23,27% lebih ekonomis.
Dari permasalahan ini dalam operasi ekonomis pembangkitan di Bali digunakan perpaduan antara metode Fuzzy Logic dan Algoritma Genetika. Fuzzy Logic digunakan untuk menentukan unit pembangkit yang optimum dalam melayani beban, karena fuzzy logic mampu menyelesaikan permasalahan dan pembuatan keputusan yang sangat kompleks. Proses penjadwalan ekonomis (economic dispatch)
p-ISSN:1693 – 2951; e-ISSN: 2503-2372
menggunakan metode algoritma genetika, karena algoritma genetika mampu menyelesaikan economic dispatch dengan pendekatan yang lebih akurat [5]. Jadi optimasi yang dilakukan algoritma genetik lebih mendekati kondisi sesungguhnya.
-
II. ECONOMIC DISPATCH
Economic dispatch adalah masalah yang penting dalam pengoperasian sistem tenaga listrik. Dalam economic dispatch ditentukan pembagian beban yang optimal diantara unit-unit pembangkit yang beroperasi setiap saat terjadi perubahan beban sehingga diperoleh total biaya operasi yang minimum dengan tetap memperhatikan batas-batas teknis dan operasional yaitu pembangkitan minimum dan maksimum setiap unit generator dan permintaan beban serta rugi-rugi transmisi [6].
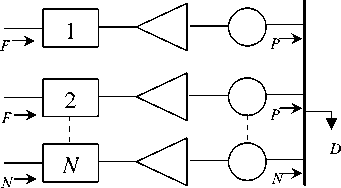
Gambar 1: Konfigurasi pembangkitanyang menyuplai beban dalam 1 bus
F = F1(P1) + F2(P2) + … + FN(PN)
P1 + P2 + … + PN = D
(1)
(2)
dengan:
N = Jumlah pembangkit yang beroperasi dan siap menyuplai beban
Pn = Daya yang dibangkitkan oleh pembangkit ke n
(MW)
Fn(Pn) = Biaya variable / biaya produksi untuk
membangkitkan daya listrik sebesar Pn dari generator ke n ($/h)
D = Demand
Secara umum fungsi biaya dari tiap pembangkit dapat diformulasikan secara matematis sebagai suatu fungsi obyektif seperti yang diberikan pada persamaan berikut [8]:
FT = Σ⅛l(≈i + bipCi + ciplGi^ (3)
dengan :
FT = total biaya pembangkitan (Rp)
ai, bi, ci = koefisien biaya dari pembangkit i
PGi = output pembangkit i (MW)
N = jumlah unit pembangkit
i = indeks dari unit pembangkitan yang berputar
-
1. Pengumpulan data beban yang diambil di PT. Indonesia Power – Unit Bisnis Pembangkit (UBP) Bali yang berupa jumlah pembangkit, data kapasitas pembangkit, beban pelanggan, dan batas maksimum-minimum pembangkitan.
-
2. Memilih pembangkit sesuai dengan pembangkit yang dapat beroperasi.
-
3. Inisialisasi nilai Load Capacity Generator dan Incremental Cost sebagai input pada fuzzy logic. Load Capacity Generator adalah Beban Kapasitas Generator dan Incremental Cost adalah sebagai Biaya Pembangkitan.
-
4. Fuzzyfikasi nilai Load Capacity Generator dan Incremental dengan output New Load Capacity. New Load Capacity atau kapasitas beban baru yang hasilnya akan dipakai untuk menentukan pembangkit mana saja yang dipakai untuk dilanjutkan ke proses algoritma genetika.
-
5. Membuat aturan-aturan if-then rule pada basis pengetahuan fuzzy yang akan dimasukan pada mesin inferensi [7].
-
6. Proses mesin inferensi merubah nilai-nilai linguistik kembali ke nilai pasti (Cripst Output) melaui proses defuzzyfikasi.
-
7. Defuzzyfikasi hasil dari nilai-nilai mesin inferensi dan mendapatkan hasil dari New Load Capacity.
-
8. Memasukkan nilai New Load Capacity hasil dari fuzzy logic sebagai populasi awal pada proses selanjutnya yaitu pada algoritma genetika.
-
9. Memasukkan nilai populasi awal ke fungsi fitness dan mendapatkan nilai populasi pertama.
-
10. Melakukan proses linear fitness rangking.
Proses ini bertujuan untuk menghindari kecenderungan konvergen pada optimal lokal, maka akan diperoleh nilai fitness baru yang lebih baik, yaitu yang memiliki variasi tinggi.
-
11. Seleksi menggunakan roulette wheel.
Memilih dua buah kromosom sebagai orang tua, umumnya dilakukan secara proposional sesuai dengan nilai fitness-nya.
-
12. Proses pindah silang (crossover).
Pindah silang ini akan memilih individu secara acak sebagai orang tua untuk memproduksi individu baru.
-
13. Melakukan proses mutasi dan mendapatkan nilai populasi baru. Mutasi terjadi secara random pada setiap gen dalam kromosom untuk menghindari individu yang memiliki nilai 0.
-
14. Mengulang proses menghitung fitness sampai proses mutasi sampai generasi sama dengan jumlah generasi total.
-
15. Memilih nilai fitness terbaik.
Diagram alir penelitian seperti dalam gambar 2 .
III. METODE PENELITIAN
Metode yang digunakan dalam analisis hasil penelitian ini adalah langkah-langkah sebagai berikut :
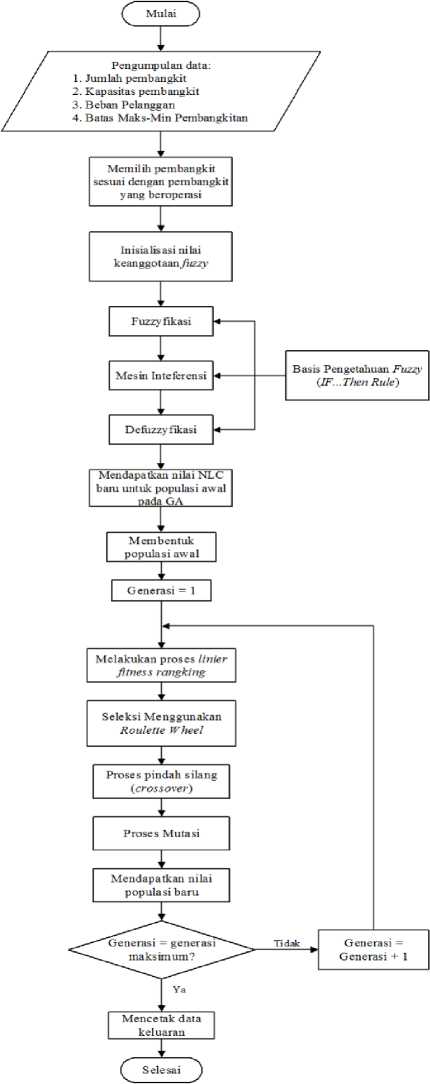
Gambar 2: Alur penelitian
-
A. Proses Fuzzy pada Matlab untuk pembangkitan ekonomis
Proses fuzzzy pada pemilihan unit pembangkit dilakukan untuk mendapatkan nilai pembangkitan baru yang akan di optimasi sehingga hasil dari algoritma genetika menjadi lebih efisein. Gambar dibawah ini menampilkan proses awal fuzzy, yaitu FIS editor yang menggambarkan input dan output yang akan digunakan.
Nasrul Faisal: Implementasi Fuzzy Logic dan Algoritma…
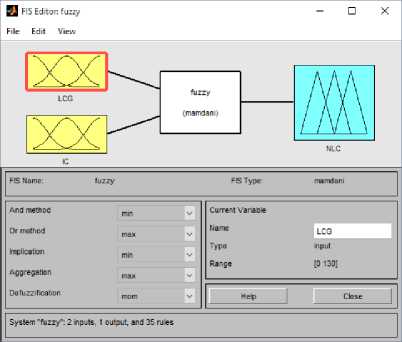
Gambar 3: Tampilan FIS Editor pada software MATLAB
Pada FIS editor ini ditentukan jumlah input, output dan metode fuzzy apa yang dipakai untuk menyelesaikan masalah. Pada studi ini memakai 2 input yaitu “LCG” diasumsikan sebagai Load Capacity Generator atau kapasitas beban generator dan “IC” yaitu Incremental Cost. Kedua inputan ini digunakan untuk mendapatkan nilai kapasitas beban baru. Pada sisi output adalah “NLC” yang kita asumsikan sebagai New Load Capacity atau kapasitas beban baru yang hasilnya akan dipakai untuk menentukan pembangkit mana saja yang dipakai untuk dilanjutkan ke proses algoritma genetika.
Berikut ini adalah urutan proses fuzzy pada matlab untuk pembebanan ekonomis.
-
1) Membership Function Editor pada MATLAB: Fungsi keanggotaan digunakan untuk menentukan batasan (range) pada variabel dan menentukan nilai parameter input dan output pada setiap variabel.
-
2) Rule Editor: Rule editor merupakan proses pada toolbox fuzzy untuk memasukan aturan-aturan fuzzy berupa (if…then rule). Untuk mendapatkan nilai beban pembangkitan baru atau “NLC” terdapat 3 variabel fuzzy yaitu berupa 2 masukan dan 1 keluaran. Tabel I di bawah ini akan menjelaskan aturan fuzzy yang digunakan dalam penelitian ini.
TABEL I
ATURAN FUZZY LOGIC UNTUK PENJADWALAN EKONOMIS
|
Aturan |
LCG |
IC |
NLC |
Aturan |
LCG |
IC |
NLC |
|
1 |
VL |
VL |
VL |
19 |
AV |
H |
AV |
|
2 |
VL |
L |
VL |
20 |
AV |
VH |
AV |
|
3 |
VL |
M |
VL |
21 |
AAV |
VL |
AAV |
|
4 |
VL |
H |
VL |
22 |
AAV |
L |
AAV |
|
5 |
VL |
VH |
VL |
23 |
AAV |
M |
AAV |
|
6 |
L |
VL |
L |
24 |
AAV |
H |
AAV |
|
7 |
L |
L |
L |
25 |
AAV |
VH |
AAV |
|
8 |
L |
M |
L |
26 |
H |
VL |
H |
|
9 |
L |
H |
L |
27 |
H |
L |
H |
|
10 |
L |
VH |
L |
28 |
H |
M |
H |
|
11 |
BAV |
VL |
BAV |
29 |
H |
H |
H |
|
12 |
BAV |
L |
BAV |
30 |
H |
VH |
H |
|
13 |
BAV |
M |
BAV |
31 |
VH |
VL |
VH |
|
14 |
BAV |
H |
BAV |
32 |
VH |
L |
VH |
|
15 |
BAV |
VH |
BAV |
33 |
VH |
M |
VH |
|
16 |
AV |
VL |
AV |
34 |
VH |
H |
VH |
|
17 |
AV |
L |
AV |
35 |
VH |
VH |
VH |
|
18 |
AV |
M |
AV |
-
3) Rule Viewer Proses: Tahap terakhir proses fuzzy pada toolbox MATLAB adalah rule viewer proses. Data jumlah Load Capacity Generator dan Incremental Cost dimasukan pada kolom input. Setelah memasukan nilai Load Capacity p-ISSN:1693 – 2951; e-ISSN: 2503-2372
Generator yang diambil dari tabel III dan Incremental Cost dari tabel IV maka nilai output New Load Capacity akan keluar diatas kurva NLC, untuk lebih jelasnya dapat dilihat pada gambar 4.
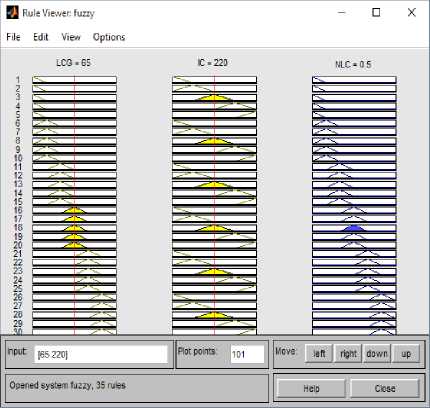
Gambar 4: Rule Viewer pada Software MATLAB
Hasil dari proses pemrograman fuzzy pada gambar 4 kemudian dihitung untuk mendapatkan hasil pembangkitan yang baru untuk dilanjutkan pada proses optimasi menggunakan algoritma genetika.
Nilai dari input IC diambil dari tabel II yaitu tabel biaya pembangkitan. Tabel II dibawah ini menunjukkan total biaya masing-masing pembangkit untuk setiap Rp/MWh :
TABEL II
BIAYA MASING-MASING PEMBANGKIT
|
UNIT |
Kapasitas Pembangkit |
Incremental Cost |
|
MW |
Rp/MWh | |
|
PLTG-Pesanggaran |
111,95 |
2.168.100 |
|
PLTG-Gilimanuk |
130 |
2.216.280 |
|
PLTG-Pemaron |
80 |
667.640 |
|
PLTD- BOO Pemaron |
125 |
3.257.750 |
|
PLTD A 30 MW Pesanggaran |
30 |
885.860 |
|
PLTD B 50 MW Pesanggaran |
50 |
1.143.100 |
|
PLTD C 50 MW Pesanggaran |
50 |
1.143.100 |
|
PLTD D 45 MW Pesanggaran |
45 |
1.128.790 |
|
PLTD F 45 MW Pesanggaran |
45 |
1.128.790 |
Sedangkan untuk nilai dari input LCG diambil dari tabel III yang dimulai pada pukul 18.00 sampai pukul 22.00. Di bawah ini akan ditampilkan sampel eksisting di lapangan berdasarkan pembebanan pada masing-masing pembangkitan.
TABEL III
DATA EKSISTING PEMBEBANAN MASING-MASING PEMBANGKIT
|
UNIT |
Pukul | |||||||
|
18.00 |
18.30 |
19.00 |
19.30 |
20.00 |
20.30 |
21.00 |
22.00 | |
|
MW |
MW |
MW |
MW |
MW |
MW |
MW |
MW | |
|
PLTG- Pesanggaran |
104,5 |
105 |
106 |
106,1 |
106,1 |
89,6 |
89,6 |
73 |
|
PLTG-Gilimanuk |
84 |
100 |
100 |
100 |
100 |
100 |
100 |
85 |
|
PLTG- Pemaron |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
PLTD- BOO Pemaron |
33,1 |
65,8 |
112,6 |
97,7 |
97,7 |
98,7 |
98,7 |
84 |
|
PLTD A 30 MW Pesanggaran |
26,1 |
26,1 |
26,1 |
26,1 |
26,1 |
26,1 |
26,1 |
26,1 |
|
PLTD B 50 MW Pesanggaran |
48,8 |
48,8 |
48,8 |
48,8 |
48,8 |
48,8 |
48,8 |
48,8 |
|
PLTD C 50 MW Pesanggaran |
48,8 |
48,8 |
48,8 |
48,8 |
48,8 |
48,8 |
48,8 |
48,8 |
|
PLTD D 45 MW Pesanggaran |
42 |
42 |
42 |
42 |
42 |
42 |
42 |
42 |
|
PLTD F 45 MW Pesanggaran |
41,8 |
42,7 |
42,7 |
42 |
42 |
40,1 |
40,1 |
41,6 |
|
Total |
429,1 |
479,2 |
527 |
511,5 |
511,5 |
494,1 |
494,1 |
449,3 |
Dari data-data diatas maka akan kita hitung untuk mendapatkan hasil pembangkitan yang baru untuk dilanjutkan pada proses optimasi menggunakan algoritma genetika.
Contoh:
PLTG-Pesanggaran : LCG ∩ IC = nilai NLC
104 ∩ 2.168.100 = 0,83
Nilai ouput NLC × max LCG = 0,83 × 111,95
= 92,9 MW
Dengan menggunakan cara yang sama dengan perhitungan manual maka didapat hasil seperti pada tabel II dibawah ini:
B. Proses Algoritma Genetika pada MATLAB
1) Inisialisasi Populasi: Tujuan inisialisasi populasi adalah untuk membangkitkan sebuah populasi yang berisi sejumlah kromosom. Pada kode program terdapat perintah (rand(1,nind0)*gaDat.NIND), kode program ini
TABEL IV
HASIL PERHITUNGAN KEUARAN FUZZY LOGIC BEBAN PEMBANGKITAN BARU
|
UNIT |
Pukul | |||||||
|
18.00 |
18.30 |
19.00 |
19.30 |
20.00 |
20.30 |
21.00 |
22.00 | |
|
MW |
MW |
MW |
MW |
MW |
MW |
MW |
MW | |
|
PLTG-Pesanggaran |
92,9 |
99,6 |
99,6 |
99,6 |
99,6 |
79,8 |
79,8 |
60 |
|
PLTG-Gilimanuk |
87,1 |
107,9 |
107,9 |
107,9 |
107,9 |
107,9 |
107,9 |
87,1 |
|
PLTG- Pemaron |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
PLTD- BOO Pemaron |
31,8 |
39,6 |
115,2 |
100,2 |
100,2 |
100,2 |
100,2 |
79,8 |
|
PLTD A 30 MW Pesanggaran |
25,05 |
25,05 |
25,05 |
25,05 |
25,05 |
25,05 |
25,05 |
25,05 |
|
PLTD B 50 MW Pesanggaran |
48,3 |
48,3 |
48,3 |
48,3 |
48,3 |
48,3 |
48,3 |
48,3 |
|
PLTD C 50 MW Pesanggaran |
48,3 |
48,3 |
48,3 |
48,3 |
48,3 |
48,3 |
48,3 |
48,3 |
|
PLTD D 45 MW Pesanggaran |
42,9 |
42,9 |
42,9 |
42,9 |
42,9 |
42,9 |
42,9 |
42,9 |
|
PLTD F 45 MW Pesanggaran |
42,7 |
43,2 |
43,2 |
42,9 |
42,9 |
36,6 |
36,6 |
42,7 |
menghasilkan matriks dua dimensi berukuran NIND x MAXGEN yang berisi nilai real dalam interval [0,1]. gaDat2.indini=([30 25])merupakan perintah untuk memasukan nilai sejumlah Pmax dan beban pada pembangkit.
-
2) Dekode Kromosom: Kromosom disini merupakan sebuah matriks berukuran 1 x JumGen atau biasa dikenal dengan vektor baris. Nvar adalah jumlah variabel yang terdapat pada fungsi yang dioptimasi. Nbit merupakan jumlah bit yang digunakan untuk mengkodekan suatu variable. Ub adalah batas atas interval, sedangkan lb merupakan batas bawah interval. Keluaran dari fungsi ini adalah nilai x, yaitu sebuah individu yang bernilai real dalam interval [ub,lb]. Jika Nvar sama dengan 2 dan Nbit sama dengan 10, maka individu x terdiri dari 2 kolom, x(1) dan x(2).
-
3) Penentuan Fungsi Firness: Untuk menjaga agar individu bernilai fitness tertinggi tidak hilang selama evolusi, maka perlu dilakukan prosedur elitisme, dengan cara membuat satu copy dari individu bernilai fitness tertinggi. Elitisme dilakukan dengan mengkopi satu atau dua individu terbaik dari populasi.
-
4) Linear Fitness Rangking: Untuk menghindari kecenderungan konvergen pada optimal lokal, maka digunakan penskalaan nilai fitness, sehingga diperoleh nilai fitness baru yang lebih baik, yaitu yang memiliki variasi tinggi [9].
-
5) Seleksi: Pada penjadwalan ekonomis ini menggunakan metode roulette wheel dimana dibuat interval komulatif (dalam interval 0-1) dari nilai fitness masing-masing kromosom. Sebuah kromosom akan terpilih jika bilangan random yang dibangkitkan berada dalam interval komulatifnya.
-
6) Pindah Silang: Operator ini memilih individu secara acak sebagai orang tua untuk memproduksi individu baru. Sebuah bilangan antara 1 sampai MAXGEN dibangkitkan secara acak dan disimpan dalam variable NewChrom.
-
7) Mutasi: Mutasi terjadi secara random pada setiap gen dalam kromosom untuk menghindari individu yang memiliki nilai 0. Jika bilangan random [0,1] yang dibangkitkan oleh perintah rand kurang dari probabilitas mutasi MutMx, maka gen yang bersesuaian akan diganti dengan nilai kebalikannya (nilai 0 diubah menjadi 1, dan 1 diubah menjadi 0). Keluaran dari fungsi mutasi ini adalah NewChrom, yaitu kromosom hasil mutasi.
-
IV. SIMULASI DAN PEMBAHASAN
-
A. Data Pembangkitan Bali
-
1) Data Kapasitas Pembangkitan: Pembangkitan di Bali disuplai oleh beberapa pembangkit. Setiap pembangkit memiliki kapasitas maksimum dan minimum yang tidak boleh terbebani melebihi dari kapsitas maksimum dan minimum tersebut. Berikut ini adalah unit pembangkit PT. Indonesia Power UBP Bali :
TABEL V
DATA KAPASITAS PEMBANGKITAN
|
No. |
Unit |
Daya Terpasang (MW) |
Daya Mampu (MW) |
|
I |
PLTG PESANGGARAN |
125,45 |
111,95 |
|
II |
PLTG GILIMANUK |
133,80 |
130,00 |
|
II |
PLTG PEMARON |
97,6 |
90,00 |
|
IV |
PLTD A 30 MW PESANGGARAN |
34,56 |
26,00 |
|
V |
PLTD B 50 MW PESANGGARAN |
54,00 |
50,40 |
|
VI |
PLTD C 50 MW PESANGGARAN |
60,80 |
51 |
|
VII |
PLTD D 45 MW PESANGGARAN |
52,80 |
45,00 |
|
VIII |
PLTD 35 MW PEMARON |
39,95 |
35,00 |
|
IX |
PLTD 45 MW PEMARON |
51,00 |
45,00 |
|
X |
PLTD 45 MW PEMARON |
51,00 |
45,00 |
|
XI |
PLTD F 45 MW PESANGGARAN |
44,65 |
45 |
-
2) Data Beban: Untuk mengoprasikan pembangkit tentunya diperlukan data beban dari sistem Bali agar dapat mengetahui pembangkit mana yang paling optimal untuk membebani. Berikut ini merupakan rincian mengenai jumlah beban pelanggan setiap jamnya dalam 1 hari pada tanggal 18 Mei 2014 yang didapat dari PT. Indonesia Power UBP Bali:
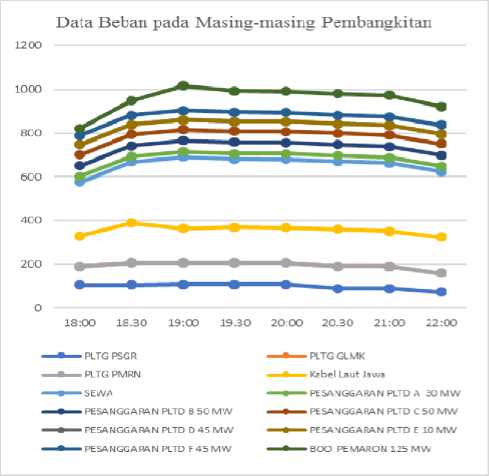
Gambar 5: Data beban pada masing-masing pembangkitan
-
3) Batas Maksimum dan Minimum Pembangkitan: Setiap pembangkit memiliki batas maksimum dan minimum yang berbeda–beda [2]. Untuk melakukan optimasi diperlukan karakteristik inputan maksimum dan minimum pada masing– masing pembangkit. Batas maksimum dan minimum ini digunakan untuk membangkitkan setiap pembangkit agar tidak melebihi dari batas yang telah ditentukan untuk masing-masing pembangkit. Berikut adalah batas maksimum dan minimum pada setiap pembangkit yang akan ditunjukkan pada gambar 6 yang didapat dari PT. Indonesia Power UBP Bali:
Nasrul Faisal: Implementasi Fuzzy Logic dan Algoritma…
p-ISSN:1693 – 2951; e-ISSN: 2503-2372

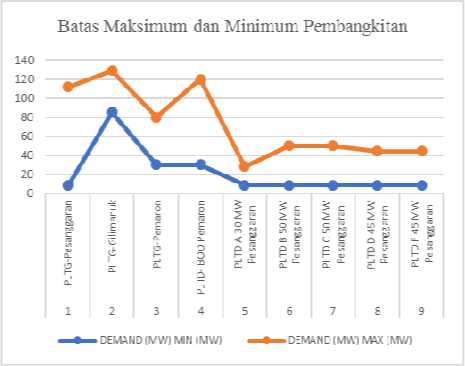
Gambar 6: Batas maksimum dan minimum pembangkitan
-
B. Hasil Optimasi Kombinasi Fuzzy Logic dan Algoritma Genetika
Penelitian ini mengambil sampel data pada 1 Mei 2014 PT. Indonesia Power UBP Bali selama 8 periode pembebanan yang dimulai pukul 18.00 sampai dengan pukul 22.00 Waktu Indonesia Bagian Tengah. Selama 8 periode tersebut Bali sedang mengalami beban yang tinggi, maka untuk itu perlu dilakukannya optimasi.
Untuk mengetahui hasil dari alokasi pembebanan masing-masing unit pembangkit dengan menggunakan Algoritma Genetika, kita memerlukan beberapa masukan seperti batas maksimum dan minimum pada masing-masing pembangkit serta populasi awal. Populasi awal didapat dari hasil pemrograman fuzzy yang telah kita lakukan sebelumnya.
Hasil dari optimasi alokasi pembebanan menggunakan kombinasi fuzzy logic dan algoritma genetika pada pembangkitan Bali dapat dilihat pada gambar 7 berikut:
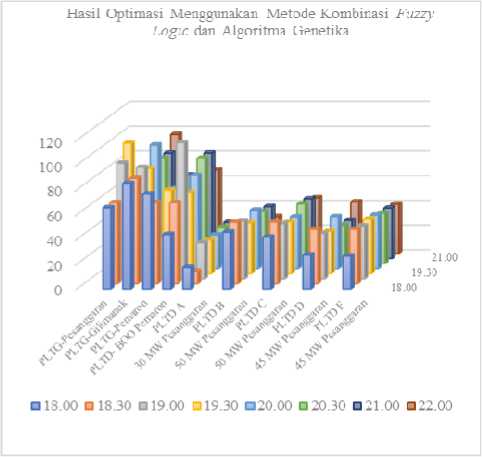
Gambar 7: Hasil optimasi menggunakan metode kombinasi fuzzy logic dan algoritma genetika
Besar biaya bahan bakar hasil optimasi menggunakan metode kombinasi Fuzzy Logic dan Algoritma Genetika dapat ditunjukkan pada tabel VI dibawah ini.
TABEL VI
BIAYA PEMBANGKITAN SELAMA 8 PERIODE MENGGUNAKAN METODE KOMBINASI FUZZY LOGIC DAN ALGORITMA GENETIKA
|
UNIT |
BIAYA PEMBANGKITAN | |||||||
|
Pukul | ||||||||
|
18:00 |
18:30 |
19:00 |
19:30 |
20:00 |
20:30 |
21:00 |
22:00 | |
|
PLTG- Pesanggaran |
39.893.040 |
148.514.850 |
242.718.795 |
218.544.480 |
218.544.480 |
180.819.540 |
180.819.540 |
83.688.660 |
|
PLTG-Gilimanuk |
788.383.800 |
188.383.800 |
198.024.618 |
188.383.800 |
188.383.800 |
188.383.800 |
188.383.800 |
188.383.800 |
|
PLTG- Pemaron |
53.411.200 |
53.411.200 |
53.411.200 |
53.411.200 |
53.411.200 |
53.411.200 |
53.411.200 |
53.411.200 |
|
PLTD- BOO Pemaron |
97.732.500 |
97.732.500 |
97.732.500 |
97.732.500 |
97.732.500 |
97.732.500 |
97.732.500 |
97.732.500 |
|
PLTD A 30 MW Pesanggaran |
24.804.080 |
24.804.080 |
24.804.080 |
24.804.080 |
24.804.080 |
24.804.080 |
24.804.080 |
24.804.080 |
|
PLTD B 50 MW Pesanggaran |
56.926.380 |
56.926.380 |
56.926.380 |
56.926.380 |
56.926.380 |
56.926.380 |
56.926.380 |
56.926.380 |
|
PLTD C 50 MW Pesanggaran |
56.926.380 |
56.926.380 |
56.926.380 |
56.926.380 |
56.926.380 |
56.926.380 |
56.926.380 |
56.926.380 |
|
PLTD D 45 MW Pesanggaran |
49.723.200 |
49.723.200 |
49.723.200 |
49.723.200 |
49.723.200 |
49.723.200 |
49.723.200 |
49.723.200 |
|
PLTD F 45 MW Pesanggaran |
49.723.200 |
49.723.200 |
49.723.200 |
49.723.200 |
49.723.200 |
49.723.200 |
49.723.200 |
49.723.200 |
|
Total |
617.523.779 |
726.145.589 |
829.990.352 |
796.175.219 |
796.175.219 |
758.450.279 |
758.450.279 |
661.319.399 |
Dapat ditunjukkan pada tabel diatas nilai dari biaya bahan menekan biaya dan pembangkitan. Pembangkitan yang bakar (incremental cost) hasil optimasi menggunakan metode memiliki biaya yang lebih rendah dibebani mendekati batas kombinasi fuzzy logic dan algoritma genetika mampu maksimumnya.
TABEL VII
PERBANDINGAN BIAYA METODE KOMBINASI FUZZY LOGIC DAN ALGORITMA GENETIKA DENGANDATA EKSISTING DI LAPANGAN
|
JAM KE |
Total Biaya Bahan Bakar (Rp) | |
|
Fuzzy& GA (Rp) |
Data Riil Lapangan (Rp) | |
|
18.00 |
617,523,779 |
749.845.603 |
|
18.30 |
726,145,589 |
893.934.469 |
|
19.00 |
829,990,352 |
1.006.565.269 |
|
19.30 |
796,175,219 |
999.451.451 |
|
20.00 |
796,175,219 |
999.451.451 |
|
20.30 |
758,450,279 |
964.790.850 |
|
21.00 |
758,450,279 |
964.790.850 |
|
22.00 |
661,319,399 |
964.790.850 |
|
TOTAL |
5,944,230,115 |
7.543.620.793 |
-
[5] S. Gunawan, Y Mulyadi, J. Kustija. “Optimasi Penjadwalan Pembangkit Termal Sistem 500 Kv Jawa – Bali Berbasis Komputasi Cerdas”. Jurnal ELEKTRANS Pendidikan Teknik Elektro Universitas Pendidikan Indonesia, Vol. 13, No. 1, Mar. 2014.
-
[6] Adrianti. “Penjadwalan Ekonomis Pembangkit Thermal dengan Memperhitungkan Rugi-Rugi Saluran Transmisi Menggunakan Metode Algoritma Genetik” Jurnal Teknik ElektroUniversitas Andalas, Vol.1. No.33, Apr. 2010.
-
[7] Kusumadewi. Analisa dan Desain Sistem Fuzzy Menggunakan Toolbox Matlab.Yogyakarta: Graha Ilmu.
-
[8] A. J. Wood. “Power Generation, Operation, and Control Second Edition”. New York: Fairmont Press & Marcel Dekker, 1996.
-
[9] Zukhri. Algoritma Genetika Metode Komputasi Evolusioner untuk Menyelesaikan Masalah Optimasi.Yogyakarta, 2013
Dapat dilihat bahwa total biaya yang dikeluarkan bila menggunakan metode kombinasi fuzzy logic dan algoritma genetika sebesar Rp. 5.944.230.115,-. Hal ini menunjukkan bahwa penggunaan metode kombinasi fuzzy logic dan algoritma genetika lebih kecil bila dibandingkan dengan data eksisting di lapangan dengan total biaya sebesar Rp. 7.543.620.793,-. Dengan diketahui besar pembebanan setiap unit yang beroperasi maka dapat ditentukan biaya bahan bakar untuk masing-masing unit pembangkit tersebut dengan menggunakan persamaan fungsi obyektif Fi(Pi).
-
V. KESIMPULAN
Kesimpulan yang dapat diambil adalah dari data eksisting di lapangan menunjukkan total biaya pembangkitan sebesar Rp. 7.543.620.793,-. Sedangkan total biaya yang dikeluarkan bila menggunakan metode kombinasi fuzzy logic dan algoritma genetika sebesar Rp. 5.944.230.115,-. Hal ini menunjukkan bahwa penggunaan metode kombinasi fuzzy logic dan algoritma genetika lebih kecil bila dibandingkan dengan data eksisting di lapangan. Dari perhitungan penurunan persentase dapat dilihat bahwa total biaya hasil optimasi metode kombinasi fuzzy logic dan algoritma genetika lebih kecil 21,202% bila dibandingkan dengan total biaya di eksisting.
REFERENSI
-
[1] Data Pembangkitan dan Beban Sistem Bali, PT. PLN (Persero), Jan. 2016.
-
[2] R. S. Hartati, I. W. Sukerayasa. “Alokasi Pembebanan Ekonomis pada Sistem Pembangkitan di Bali dengan Metode Jaringan Syaraf Tiruan”. Jurnal TRANSISTOR, Vol 5. No. 1. Jul. 2005”.
-
[3] D. Rumana, Hermawan, M. Facta. “Implementasi Algoritma Genetik dalam Economic Dispacth dengan Valve Point Loading”. Jurnal Teknik Elektro Universitas Diponegoro.
-
[4] R. N. Marifah, Y. Mulyadi, A. G. Abdullah. “Operasi Ekonomis Pembangkit Thermal Sistem 500KV Jawa-Bali dengan Pendekatan Algoritma Fuzzy Logic”Jurnal ELEKTRANS Pendidikan Teknik Elektro Universitas Pendidikan Indonesia, Vol.12, No.2, Sept. 2013.
Nasrul Faisal: Implementasi Fuzzy Logic dan Algoritma…
p-ISSN:1693 – 2951; e-ISSN: 2503-2372

Discussion and feedback