Unjuk Kerja Kode Hybrid Orthogonal Small Set
on
Teknologi Elektro, Vol.15, No.1,Januari – Juni 2016
117
Unjuk Kerja Kode Hybrid Orthogonal Small Set
Nyoman Pramaita
Abstract—In this paper, the performance metrics of the hybrid orthogonal small set code sequence for 16 chip lengths is evaluated. The author demonstrates that auto-correlation function (ACF) and cross-correlation function (CCF) of the hybrid code sequence are comparable with that of the existing orthogonal small set Kasami code sequence. The hybrid code sequence has slightly worse BER performance than that of the existing orthogonal small set Kasami code sequence under frequency selective fading channel in synchronous CDMA system. However, the hybrid code sequence possesses more number of orthogonal codes in a chip set, hence it can accomodate more number of users in a base station. Therefore, the hybrid code is more appropriate for synchronous CDMA systems.
Intisari—Pada penelitian ini, unjuk kerja kode hybrid orthogonal small set dengan panjang 16 chip dievaluasi. Hasil penelitian menunjukkan bahwa auto-correlation function (ACF) and cross-correlation function (CCF) kode hybrid hampir sama dengan kode existing orthogonal small set Kasami. Kode existing orthogonal small set Kasami memiliki unjuk kerja BER (bit error rate) sedikit lebih baik dari pada kode hybrid orthogonal small set pada kondisi kanal Rayleigh frequency selective fading dalam sistem synchronous CDMA. Namun, kode hybrid orthogonal small set memiliki jumlah kode lebih banyak dalam chip set, karenanya dapat menampung lebih banyak user pada suatu base station. Sehingga, kode hybrid orthogonal small set lebih tepat untuk diterapkan dalam sistem synchronous CDMA. .
Kata Kunci—ACF, BER, CCF, CDMA, kode orthogonal, kode spreading, Rayleigh fading
-
I. PENDAHULUAN
Sistem code division multiple access (CDMA) merupakan salah satu aplikasi teknik spread spectrum yang memerlukan kode yang unik untuk setiap user [1]-[3]. Dalam sistem synchronous CDMA atau dalam arah downlink, sinyal yang ditransmisikan oleh base station akan berisi komponen yang ditujukan untuk user yang diinginkan dan komponen untuk user yang lain, yang memakai frekuensi yang sama dalam satu
Nyoman Pramaita adalah dosen pada Teknik Elektro, Fakultas Teknik, Universitas Udayana (e-mail: pramaita@ee.unud.ac.id).
sel. Jika dilihat dari sisi user yang diinginkan, komponen sinyal yang ditujukan untuk user yang lain akan menkontribusikan noise, yang dikenal dengan multiple access interference (MAI) [4], [5]. MAI ini muncul akibat adanya cross-correlation diantara kode spreading yang dipakai oleh user, yang akan membatasi unjuk kerja sistem CDMA pada kondisi kanal yang dibatasi MAI [6].
Salah satu tujuan utama perancang sistem komunikasi wireless dalam hal ini adalah untuk menghasilkan kode spreading, yang memiliki kapasitas yang besar dan nilai crosscorrelation yang rendah agar dapat menampung jumlah user yang banyak dan untuk meminimalkan efek MAI [7].
Kode spreading biner dapat dibagi menjadi dua kategori, yaitu kode orthogonal dan non-orthogonal. Masing-masing kode spreading ini memiliki parameter yang unik seperti autocorrelation, cross-correlation, dan ukuran keluarga kode atau jumlah kode spreading dalam chip set [8].
Ketika nilai cross-correlation antara dua kode spreading dalam chip set yang sama bernilai tidak nol, kode spreading dalam chip set tersebut dikenal dengan kode non-orthogonal. Kode spreading disebut kode orthogonal jika nilai crosscorrelation antara dua kode spreading dalam chip set yang sama bernilai nol [9].
Maximal-sequence (m-sequence), kode Gold and Kasami (tiga keluarga kode spreading) merupakan kode non-orthogonal biner yang populer. Kode Walsh yang dibangkitkan dengan cara memetakan baris matrik Hadamard telah membuktikan eksistensinya sebagai kode orthogonal yang populer [7], [10]. Namun, kode orthogonal Gold, orthogonal m-sequence, dan orthogonal small set Kasami dibangkikan dengan cara yang berbeda dari kode Walsh, yaitu dari versi kode non-orthogonal masing-masing kode spreading [11]-[13].
Kode Walsh, orthogonal Gold dan orthogonal m-sequence memiliki jumlah anggota dalam chip set sama dengan panjang kode orthogonal. Namun, jumlah anggota dalam chip set dari kode existing orthogonal small set Kasami kurang dari panjang kode [12].
Dalam [14], metode hybrid merupakan kombinasi dari kode non-orthogonal m-sequence dan small set Kasami yang dapat menghasilkan kode orthogonal yang memiliki jumlah kode dalam chip set sama dengan panjang kode sepeti halnya
Nyoman Pramaita: Unjuk Kerja Kode Hybrid …
p-ISSN:1693 – 2951; e-ISSN: 2503-2372

kode Walsh, orthogonal Gold dan orthogonal m-sequence. Kode yang dihasilkan ini disebut dengan kode hybrid othogonal small set.
Pada penelitian ini, unjuk kerja kode hybrid orthogonal small set dengan panjang 16 chip dievaluasi dan dibandingkan dengan kode existing orthogonal small set Kasami.
-
II. KODE SMALL SET KASAMI
-
A. Kode Non-Orthogonal Small Set Kasami Code Sequence
Kode non-orthogonal small set Kasami dibangkitkan dari m-sequence dengan memakai algoritma yang dijelaskan pada paragraf berikut.
Jika u merupakan m-sequence dengan panjang N yang dibangkitkan oleh generator polynomial dengan level n, dan w adalah kode yang diperoleh dengan cara decimasi u dengan 2n∣2 + 1, dimana n merupakan bilangan genap dan N = 2n — 1. Maka, kode w juga merupakan m-sequence dengan panjang 2n/2 - 1. Berdasarkan kode u dan w tersebut, kode small set Kasami dinyatakan oleh persamaan (1) berikut [12]:
Ks = (u,uθw,uφΓw,... ,uQT2∙nl∣~2 w) (1)
dimana Ks menunjukkan kode small set Kasami dengan panjang N= 2n — 1; T merupakan operator cyclic shift; ® adalah operasi XOR, dan 2n∣2 — 2 parameter shift untuk kode w. Karena w and u memiliki panjang kode yang berbeda, maka harus dilakukan pengulangan N∣(2n∣2 - 1) kode w sebelum melakukan operasi XOR.
Kode smal set Kasami memiliki ukuran keluarga (M) sebesar 2n∣2 kode biner, masing-masing dengan panjang N= 2n-1.
-
B. Kode Existing Orthogonal Small Set Kasami
Kode existing orthogonal small set Kasami dibangkitkan dari kode non-orthogonal small set Kasami dengan memakai algoritma yang dijelaskan dalam [12].
Kode existing orthogonal small set Kasami dapat menghasilkan (√N + 1) N jumlah kode yang berbeda, masing-masing dengan panjang N + 1 chip, dimana √N + 1 merupakan jumlah group (set) kode. N adalah jumlah anggota dalam setiap group kode dan N= 2n — 1 untuk setiap bilangan genap n.
-
C. Kode Hybrid Orthogonal Small Set
Misalkan kode small set Kasami dan m-sequence, masing-masing dengan panjang N (N= 2n — 1 dengan n merupakan bilangan genap) dan dibangkitkan dengan memakai generator polynomial yang sama, direpresentasikan secara berurutan oleh {ki} and {uj. Dua kode ini dapat dinyatakan oleh persamaan berikut:
{kl}a = Ta{ki} = Ta(k0, k", k2.....k$-2, k$-") (2)
{ul}a = Ta{ui} = Ta(u0>ur>U2,...,uN_2 UN-i) (3)
dimana a = (0,1,2,..., N — 1) menunjukkan parameter shift; Ta{ki} dan Ta{ui} secara berurutan meyatakan cyclic shift dari kode small set Kasami and m-sequence.
{k∕} dan {u∕} seperti yang ditunjukkan dalam persamaan (2) dan (3) merupakan angka biner. Dengan mengganti bit 0 menjadi 1 dan bit 1 menjadi -1, kode hybrid diperoleh dengan cara mengalikan kode small set Kasami dengan seluruh hasil pergeseran m-sequence sebesar satu chip [14]. Pernyataan ini secara matematis diekspresikan oleh persamaan (4) berikut:
. ({kl}a × T){ul}a for 0≤j<N
{ti∏a= i{ki}a for j = N (4)
0 otherwise
dimana T1{ut}a menunjukkan cyclic shift dari kode {uf}a sebesar j chips. Seperti yang ditunjukkan dalam persamaan (4), {ki}a untuk j = N merupakan kode small set Kasami code.
Langkah-langkah berikut menggambarkan prosedur untuk mengubah kode hybrid yang dihasikan dari persamaan (4) menjadi sekelompok kode orthogonal [13]:
Langkah 1: ganti kolom yang pertama (chip yang pertama) dengan bilangan ‘1’.
Langkah 2: jika chip yang pertama seluruhnya sudah bernilai ‘1’ dan oleh karenanya tidak diubah oleh langkah 1, maka isikan ‘-1’ pada akhir kode (kolom).
Langkah 3: jika chip yang pertama seluruhnya bernilai ‘-1’dan karenanya telah diubah oleh langkah 1, maka isikan ‘1’ pada akhir kode (kolom).
Langkah 4: Ulangi langkah 1 sampai dengan 3 untuk seluruh kode yang direpresentasikan oleh persamaan (4).
Secara matematis, langkah-langkah diatas untuk mendapatkan kode orthogonal dinyatakan oleh persamaan (5) berikut:
{o(»}a = ^{s^^h^^^ (5)
dimana {s(1))a merupakan hasil matrik 'h(1)* dengan chip pertama (kolom) (h^1)) dihilangkan. Grup kode {o(1)}a adalah grup (set) kode dengan ukuran matrik sebesar (N +
1)x(N + 1) yang barisnya orthogonal satu sama lain.
Setiap nilai ‘a’ dalam persamaan (2) dan (3), dengan memakai persamaan (4) dan (5) menghasilan satu set kode orthogonal. Oleh karena itu, satu set kode orthogonal akan dihasilkan untuk setiap nilai ‘a’. Sehingga untuk seluruh nilai‘a’ akan diperoleh N set kode orthogonal.
Namun, karena kode w harus diulang sebanyak N∣ (2n∣2 - 1) sebelum dilakukan operasi XOR seperti yang dijelaskan dalam bagian 2, maka akan terdapat N∣(2n∣2 - 1) set kode orthogonal yang sama. Karena itu, kombinasi m-
sequence dan kode small set Kasami menghasilkan (2n/2 - 1) set kode orthogonal yang berbeda [14].
-
III. SIMULASI KODE HYBRID ORTHOGONAL SMALL SET
Kode hybrid orthogonal small set diimplementasikan pada sistem synchronous CDMA, melalui simulasi dengan memakai pemrograman Matlab. Unjuk kerja BER (bit error rate) kode hybrid orthogonal small set dengan panjang 16 chip, dievaluasi dan dibandingkan dengan kode existing orthogonal small set Kasami. Beberapa asumsi dibuat untuk simulasi sistem synchronous CDMA, yang dinyatakan pada bagian B. Blok diagram yang dipakai untuk mensimulasikan sistem synchronous CDMA ditunjukkan pada bagian A. Jumlah simulasi Monte Carlo untuk sistem ini adalah 10 kali.
-
A. Blok Diagram Sistem
Blok diagram model simulasi yang digunakan ditunjukkan dalam gambar 1. Simulasi ini dilakukan pada kondisi kanal Rayleigh frequency selective fading.
-
B. Asumsi Simulasi Untuk Kode Hybrid Orthogonal Small Set Pada Sistem Synchronous CDMA
Berdasarkan blok diagram model simulasi yang ditunjukkan dalam gambar 1, dibuat asumsi simulasi sebagai berikut:
-
• Jumlah bit input sebanyak 10000 bit.
-
• Modulasi yang dipakai adalah modulasi BPSK.
-
• Jumlah user yang dipakai sebanyak total jumlah kode dalam set kode, yaitu 16 untuk kode hybrid dan 15 untuk kode existing.
-
• Panjang kode diasumsikan sebesar 16 chip.
-
• Penerima yang dipakai adalah Rake receiver.
-
• Sinyal MAI dan sinyal yang diinginkan diasumsikan sinkron chip per chip di penerima..
-
• Tidak adanya interferensi dari sel-sel tetangga.
-
• Kanal Rayleigh frequency selective fading dimodelkan dengan tiga path time delay (0 , 1 durasi chip, 2 durasi chip) dan tiga path gain (0 dB, -6 dB -9 dB).
-
IV. HASIL DAN DISKUSI
Pada bagian berikut, unjuk kerja kode hybrid orthogonal small set yang disimulasikan memakai pemrograman Matlab, dibandingkan dengan unjuk kerja kode existing orthogonal small set Kasami.
-
A. Autocorrelation Function Kode Hybrid orthogonal small set
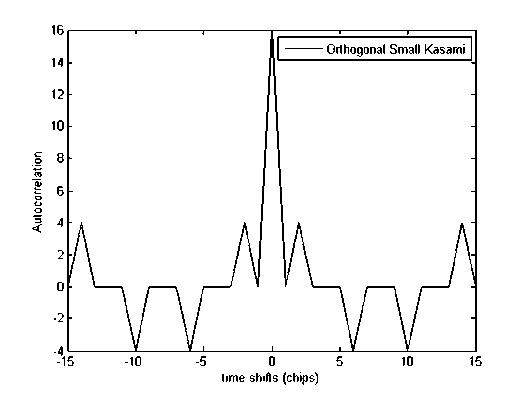
Autocorrelation function (ACF) kode hybrid orthogonal small set dan kode existing orthogonal small set Kasami dengan panjang 16 chip secara berurutan ditunjukkan dalam gambar 2 dan gambar 3.
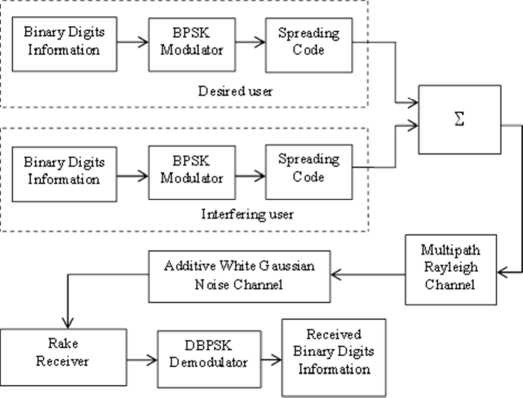
Gambar 1. Block diagram untuk simulasi sistem synchronous CDMA
16Γ
14 -
12 -
10 -
8 -
6 -
4 -
I The proposed code ∣
-15 -10 -5 0 5 10 15
time shifts (chips)
Gambar 2. ACF kode hybrid
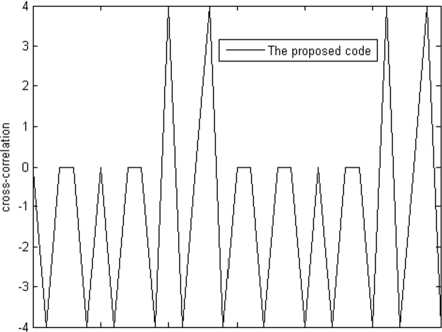
Seperti yang ditunjukkan gambar 2 dan gambar 3, pada pergeseran waktu nol (tidak adanya pergeseran chip), kode hybrid maupun kode existing memiliki nilai autocorrelation yang maksimum. Hal ini disebabkan, nilai autocorrelation diperoleh dari korelasi antara suatu kode dengan kode itu sendiri.
Namun, pada pergeseran waktu yang bukan nol (adanya pergeseran chip), nilai autocorrelation menjadi tidak maximum karena struktur chip yang berbeda antara dua kode.
Berdasarkann autocorrelation function (ACF) kedua kode orthogonal tersebut, merit factor (MF) kode hybrid dan kode existing orthogonal small set Kasami dengan panjang kode 16 chip dapat ditabulasikan dalam tabel 1.
Nyoman Pramaita: Unjuk Kerja Kode Hybrid …
p-ISSN:1693 – 2951; e-ISSN: 2503-2372

Gambar 3. ACF kode existing orthogonal small set Kasami
■15 -10 -5 0 5 10 15
time shifts (chips)
Gambar 4. CCF kode hybrid
TABEL 1
MF KODE HYBRID
|
Kode Orthogonal |
Panjang Kode (chip) |
MF |
|
Kode Hybrid |
16 |
2 |
|
Kode Existing |
16 |
2 |
TABEL 2
CM KODE HYBRID
|
Kode Orthogonal |
Panjang Kode (chip) |
CM (dB) |
|
Kode Hybrid |
16 |
-6.02 |
|
Kode Existing |
16 |
-6.02 |
Karena kedua kode orthogonal tersebut memiliki nilai MF yang sama, maka kode hybrid memiliki autocorrelation function (ACF) yang mirip dengan kode existing orthogonal small set Kasami.
-
B. Cross-correlation Function Kode Hybrid Orthogonal Small Set
Seperti yang ditunjukkan dalam gambar 4 and gambar 5, cross-correlation kedua kode orthogonal terebut pada pergeseran waktu nol (tidak adanya pergeseran chip) bernilai nol, karena kode orthogonal didefinisikan sebagai kode yang memiliki cross-correlation bernilai nol pada pergeseran waktu nol (tidak adanya pergeseran chip).
Namun, beberapa cross-correlation bernilai bukan nol pada pergeseran waktu bukan nol (adanya pergeseran chip) karena struktur chip kedua kode orthogonal tersebut telah berubah ketika adanya pergeseran chip.
Berdasarkann cross-correlation function (CCF) kedua kode orthogonal tersebut, correlation margin (CM) kode hybrid dan kode existing orthogonal small set Kasami dengan panjang kode 16 chip dapat ditabulasikan dalam tabel 2.
Seperti yang ditunjukkan dalam tabel 2, kode hybrid memiliki CM yang sama dengan kode existing orthogonal small set Kasami code sequence. Karena itu, dalam kaitannya dengan CM, kode hybrid orthogonal small set memiliki CCF mirip dengan kode existing orthogonal small set Kasami.
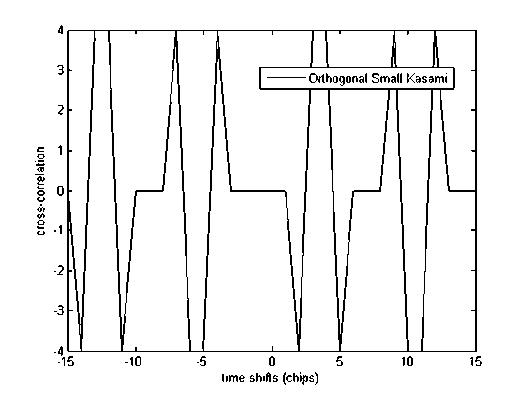
Gambar 5. CCF kode existing orthogonal small set Kasami
-
C. Unjuk Kerja BER Kode Hybrid Orthogonal Small Set Pada Kondisi Kanal Rayleigh Frequnecy Selectivet Fading
Seperti yang ditunjukkan dalam gambar 6, kode existing orthogonal small set Kasami memiliki unjuk kerja BER sedikit lebih baik dari pada kode hybrid dalam sistem synchronous CDMA pada kondisi kanal Rayleigh frequency selective fading. Hal ini dapat dijelaskan pada paragraf berikut.
Pada kondisi kanal frequency selective fading, sinyal yang diterima merupakan beberapa versi dari sinyal yang ditransmisikan, yang teredam dan tertunda. Ketika despreading sinyal yang diterima, korelasi antara komponen multipath yang pertama (tidak teredam dan tertunda) dan kode user yang diinginkan merupakan sinyal yang diinginkan.
Nyoman Pramaita: Unjuk Kerja Kode Hybrid…
Sedangkan, korelasi antara kode user yang diinginkan dan komponen multipath yang lainnya (teredam dan tertunda) merupakan sinyal yang tidak diinginkan yang kan mengganggu sinyal yang diinginkan. Nilai-nilai korelasi ini ditentukan oleh ACF dari kode yang dipakai, dimana nilai korelasi pada pergeseran waktu nol mewakili kuat sinyal yang diinginkan sedangkan pada pergeseran waktu bukan nol mewakili kuat sinyal yang tidak diinginkan (interferensi antar simbol (ISI)).
Seperti yang ditunjukkan dalam gambar 2 dan gambar 3, kode hybrid orthogonal small set dan kode existing orthogonal small set Kasami memiliki ACF yang serupa. Karena itu, kode hybrid orthogonal small set dan kode existing orthogonal small set Kasami untuk satu user memiliki nilai BER yang sama seperti yang ditunjukkan dalam gambar 7.
Namun, ketika terdapat lebih dari satu user dalam sistem CDMA, sinyal user yang diinginkan tidak hanya diganggu oleh ISI tetapi juga oleh sinyal pengganggu yang datang dari user yang lain. Kuat sinyal pengganggu yang datang dari user yang lain, ditentukan oleh nilai cross-correlation pada pergeseran waktu bukan nol pada CCF, karena nilai korelasi pada pergeseran waktu bukan nol pada CCF untuk kode orthogonal mewakili kuat sinyal dari user yang lain (user pengganggu).
Kode hybrid orthogonal small set dan kode existing orthogonal small set Kasami memiliki CCF yang serupa dalam kaitannya dengan CM (correlation margin). Namun, kode hybrid orthogonal small set dengan panjang 16 chip memiliki cross-correlation bernilai nol pada pergeseran waktu bukan nol yang terjadi lebih jarang dibandingkan dengan nilai crosscorrelation yang dimiliki kode existing orthogonal small set Kasami, seperti yang ditunjukkan dalam gambar 4 dan gambar 5. Sehingga, nilai BER untuk peningkatan jumlah user dari kode hybrid sedikit lebih besar dari pada nilai BER yang dimiliki oleh kode existing orthogonal small set Kasami seperti yang ditunjukkan dalam gambar 7. Oleh karena itu, kode existing orthogonal small set Kasami memiliki unjuk kerja BER sedikit lebih baik seperti yang ditunjukkan dalam gambar 6.
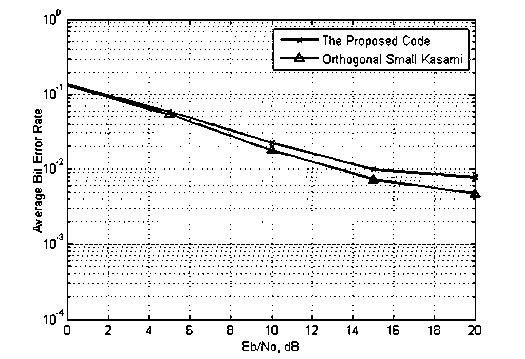
Gambar 6. BER versus SNR kode orthogonal pada kanal Rayleigh frequency
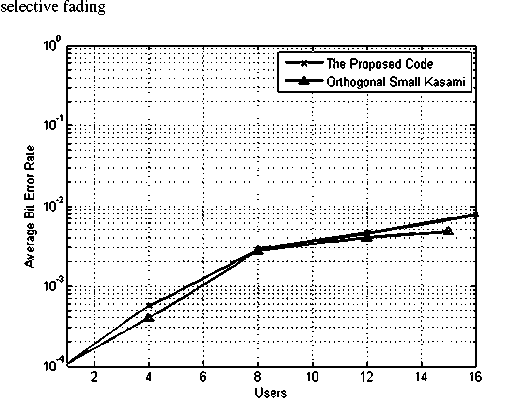
Gambar 7. BER versus jumlah user kode orthogonal pada kanal Rayleigh frequency selective fading untuk SNR = 20 dB
Namun, seperti yang ditunjukkan dalam [14], kode hybrid orthogonal small set memiliki ukuran keluarga kode yang lebih besar dalam grup (set) kode. Dalam kasus kode dengan panjang 16 chip, kode hybrid orthogonal small set memiliki 16 kode untuk menampung 16 user sedangkan kode existing orthogonal small set Kasami hanya memiliki 15 kode untuk panjang kode yang sama (16 chip).
-
V. KESIMPULAN
Unjuk kerja kode hybrid orthogonal small set telah dievaluasi dan dibandingkan dengan unjuk kerja dari kode existing orthogonal small set Kasami untuk panjang kode sebesar 16 chip.
Telah ditunjukkan bahwa autocorrelation function (ACF) dan cross-correlation function (CCF) dari kode hybrid mirip dengan ACF dan CCF yang dimiliki oleh kode existing orthogonal small set Kasami.
Implementasi kode hybrid dalam sistem synchronous CDMA pada kanal Rayleigh frequency selective fading melalui simulasi menunjukkan bahwa kode existing orthogonal small set Kasami memiliki unjuk kerja BER sedikit lebih baik dari pada kode hybrid
Namun, kode hybrid memiliki lebih banyak kode untuk menampung lebih banyak user dalam chip set (base station).
Karena itu, kode hybrid lebih tepat diimplementasikan dalam sistem synchronous CDMA.
REFERENSI
[1]
[2]
hoshyar, r., wathan, f.p., and tafazolli, r. (2008) ‘novel low-density signature for synchronous CDMA systems over AWGN channel’, IEEE Transactions on Signal Processing, Vol. 56, pp.16161626
Cheng, H., Ma, M. and Jiao, B. (2009) ‘On the design of comb spectrum code for multiple access scheme’, IEEE Transactions on Communications, Vol. 57, No. 3, pp.754-763
Nyoman Pramaita: Unjuk Kerja Kode Hybrid …
p-ISSN:1693 – 2951; e-ISSN: 2503-2372

-
[3] Nikjah, R. and Beaulieu, N.C. (2008) ‘,On antijamming in general CDMA systems–Part I: Multiuser capacity analysis’, IEEE Transactions on Wireless Communications, Vol. 7, No. 5, pp. 16461655
-
[4] Jatunov, L. and Madisetti, V.K. (2006) ‘Computationally-efficient SNR estimation for band limited wideband CDMA systems’, IEEE Transaction on Wireless Communications, Vol. 5, pp.3480-3491
-
[5] Van Houtum, W.J. (2001) ‘Quasi-synchronous code-division multiple access with high-order modulation’, IEEE Transactions on Communications, Vol. 49, No. 7, pp.1240-1249
-
[6] Adeola, F.A., Adekunle, A.S. and Peter, A.O. (2011) ‘Direct sequence CDMA system using finite-time altered sinusoidal signals as orthogonal signatures’, IEEE 3rd International Conference on Adaptive Science and Technology (ICAST 2011), pp.174 – 177
-
[7] Pal, M. and Chattopadhyay, S. (2010) ‘A novel orthogonal minimum cross-correlation spreading code in CDMA system’, IEEE International Conference on Emerging Trends in Robotics and Communication Technologies, pp.80-84
-
[8] Mollah, M.B. and Islam, Md.R. (2012) ‘Comparative analysis of Gold codes with PN codes using correlation property in CDMA technology’, IEEE International Conference on Computer Communication and Informatics (ICCCI), pp.1-6
-
[9] Ziani, A. and Medouri, A. (2012) ‘Analysis of different pseudorandom and orthogonal spreading sequences in DS-CDMA’, IEEE International Conference on Multimedia Computing and Systems (ICMCS), pp.558-564.
-
[10] Dinan, E.H. and Jabbari, B (1998) ‘Spreading codes for direct sequence CDMA and wideband CDMA cellular networks’, IEEE Communication Magazine, Vol. 36, pp.48-54.
-
[11] Tachikawa, S. (1992) ‘Recent spreading codes for spread spectrum communication systems’, Electron. Commun. Jpn., pp. 4149.
-
[12] Chandra, A. and Chattopadhyay, S. (2009) ‘Small set orthogonal Kasami codes for CDMA system’, 4th IEEE International Conference on Computers and Devices for Communication, pp.1-4.
-
[13] Donelan, H. and O’Farrell, T. (1999) ‘Method for generating sets of orthogonal sequences’, Electronic Letters, Vol. 35.
-
[14] Pramaita, N., Diafari, IGAGK., Negara, DNKP., and Dharma, A. (2015) ‘New orthogonal small set Kasami code sequence’, Journal of Electrical Technology, Vol. 14, No. 1, pp.47-51
ISSN 1693 – 2951
Nyoman Pramaita: Unjuk Kerja Kode Hybrid…
Discussion and feedback