ANALISA ALIRAN DAYA DENGAN METODE INJEKSI ARUS PADA SISTEM DISTRIBUSI 20 KV

Analisa Aliran Daya…

IBG Manuaba, K Amerta Yasa

ANALISA ALIRAN DAYA DENGAN METODE INJEKSI ARUS PADA SISTEM DISTRIBUSI 20 KV

IBG Manuaba ¹⁾, Kadek Amerta Yasa ²⁾

• ¹)    Staff pengajar Teknik Elektro Fakultas Teknik Universitas Udayana Kampus Bukit Jimbaran, Bali, 80361

• ²)    Staff pengajar Teknik Elektro Politeknik Negeri Bali

Abstrak

Metode Injeksi Arus (Current Injections Method) merupakan metode baru hasil pengembangan dari metode Newton-Raphson yang digunakan untuk menganalisa aliran daya. Metode Injeksi Arus memiliki struktur matriks Jacobian yang di-update pada setiap iterasi sehingga lebih cepat dalam melakukan analisa aliran daya.

Metode Newton Raphson dan metode Injeksi Arus dibandingkan dengan melihat hasil analisanya. Penyulang Bukit Jati, Tenganan, dan VIP 2 merupakan penyulang-penyulang yang digunakan sebagai obyek analisa aliran daya. Penyulang Bukit Jati, dan Penyulang Tenganan adalah penyulang di Area Jaringan Bali Timur, sedangkan Penyulang VIP 2 adalah penyulang di Area Jaringan Bali Selatan.

Dari hasil analisa, metode Injeksi Arus terbukti lebih cepat dan memerlukan lebih sedikit proses iterasi dibandingkan metode Newton-Raphson. Untuk hasil tegangan bus, keduanya menunjukkan hasil yang tidak berbeda jauh. Dalam semua analisa yang dilakukan, metode Injeksi Arus lebih efisien daripada metode Newton-Raphson.

Kata kunci : Analisa aliran daya, metode injeksi arus, jakobian.

• 1.    PENDAHULUAN

Aliran daya merupakan bagian penting dalam sistem distribusi. Sistem distribusi memiliki karakteristik sistem yang radial, ratio r/x yang tinggi dan beban yang tidak seimbang. Hal tersebut mengakibatkan konvergensi pada metode Newton-Raphson menjadi kurang sempurna dan memerlukan waktu yang lebih lama untuk iterasi karena matriks Jacobian dihitung empat kali di setiap bus untuk setiap iterasi (Chen, 1991).

Metode Newton-Raphson biasanya digunakan untuk menganalisa aliran daya pada sistem transmisi. Berbeda dengan metode Newton-Raphson, metode injeksi arus merupakan metode yang dikembangkan untuk menganalisa aliran daya pada sistem distribusi. Metode Injeksi Arus atau Current Injections Method (CIM) merupakan metode baru untuk studi aliran daya dan merupakan pengembangan dari metode Newton-Raphson. Metode Injeksi Arus memiliki struktur matriks Jacobian yang identik dengan matriks admitansi bus dimana elemen diagonal matriks tersebut di-update pada setiap iterasi dan elemen matriks bukan diagonalnya konstan pada setiap iterasi. Matriks bukan diagonal yang konstan menyebabkan metode injeksi arus lebih cepat dibandingkan dengan metode Newton Raphson.

Matriks Jacobian pada metode injeksi arus digunakan untuk menghitung besarnya arus injeksi dan rugi-rugi arus yang nantinya digunakan untuk menghitung besarnya daya aktif dan reaktif pada masing-masing bus beserta rugi-ruginya dan juga nantinya digunakan untuk menghitung tegangan pada setiap bus. Jika belum konvergen, maka tegangan hasil perhitungan sebelumnya digunakan kembali untuk menghitung matriks Jacobian, arus injeksi,

daya aktif maupun reaktif dan rugi-rugi sampai konvergen (Garcia, 2000).

Dalam paper ini akan ditinjau bagaimana metode Injeksi Arus digunakan untuk menganalisa aliran daya pada beberapa penyulang 20 kV di Bali. Hasil analisa metode Injeksi Arus ini akan dibandingkan dengan hasil analisa yang menggunakan metode Newton-Raphson.

• 2.    DASAR TEORI

  • 2.1    Aliran Daya Dengan Metode Injeksi Arus (

Current Injection Method /Cim)

Metode injeksi arus adalah metode baru hasil pengembangan dari metode Newton-Raphson yang digunakan untuk menyelesaikan masalah aliran daya pada saluran distribusi.

Metode injeksi arus bekerja dengan cara menginjeksi arus pada masing-masing bus dengan tujuan untuk memperkecil rugi-rugi daya pada saluran distribusi. Adapun proses injeksi arus adalah dengan menggunakan persamaan berikut (da Costa, 1999):

I = Y E           ........................... (1)

I = arus yang diinjeksi pada setiap bus

Y = matriks Jacobian dari metode injeksi arus

E = Tegangan pada setiap bus

Metode injeksi arus memiliki struktur matriks Jacobian yang identik dengan matriks admitansi bus dimana elemen diagonal matriks tersebut di-update pada setiap iterasi dan elemen matriks bukan diagonalnya konstan pada setiap iterasi. Matriks bukan diagonal yang konstan menyebabkan metode injeksi arus lebih cepat dibandingkan dengan metode Newton-Raphson. Berikut susunan matriks Jacobian pada metode injeksi arus (da Costa, 1999):

δ m 1 ∆I r 1 ∆I m 2 ∆ r 2 :	—	Yn) Y21	Y12 ( Y2k)	∙∙     Y1 n ■      Y2 n	Γ∆ Vr, ∆Vm ∆ Vr 2 . ■
∆I mn		L Yn 1	Yn2	∙  (Ynn ) _	∆ Vrn
∆I rn					∆ Vrn
J

........................... (2)

Matriks Jacobian untuk metode injeksi arus terletak pada elemen matriks admitansi bus. Untuk elemen matriks bukan diagonal, susunan matriks Jacobian-nya adalah (Garcia, 2000) :

Y

im

B G im       im

G_m - B_m

im        im

(3)

Elemen matriks bukan diagonal tidak mengalami perubahan selama proses iterasi. Struktur matriks Jacobian untuk elemen diagonal matriks admitansi bus adalah (Garcia, 2000) :

Y •

kk

B'

kk

G'

kk

G"kk

B

kk

(4)

Masing-masing elemen dari matriks Jacobian untuk elemen diagonal matriks admitansi bus mengalami perubahan selama proses iterasi. Adapun perubahan tersebut diperlihatkan dari persamaan berikut (Garcia, 2000) :

B'kk ^— Bkk ^{- a}k  (5)

G' kk — Gkk — bk  (6)

G" kk — Gkk — Ck(7)

B"kk — B_kk - dk  (8)

2.2 Persamaan Untuk Pq Bus

Matriks Jacobian pada metode injeksi arus digunakan untuk menghitung rugi-rugi arus pada setiap bus. Rugi-rugi arus pada bus k diperlihatkan pada persamaan berikut (Garcia, 2000) :

Psp _- jQ^spn

^M k = ^k (F √ -∑ YiE-= 0

(Ek )

dengan :

Ek = Vrk + J‰

sp

Pk     Pgk Plk

Qksp — Qgk - Qik

dengan :

(P_k^sp ) , (Q_k^sp ) - spesifikasi daya aktif dan reaktif pada bus k

P_gk , Q_gk      - daya aktif dan reaktif generator

P_lk , Q_lk      - daya aktif dan reaktif beban

Y_ki = G_ki + JB_ki - elemen matrik admitansi bus

Persamaan (17) disederhanakan menjadi :

δ∣rk—(∣rk) -(∣^cck^lc)

δimk=(κ) - (Ck^c)

Sehingga besarnya rugi-rugi daya aktif dan reaktif pada setiap bus sesuai dengan persamaan berikut :

∆Qk — (Qk^sp) - (Qk^alc)    

∆Pk = (Pk^sp) - (Pk^calc)

Daya aktif dan reaktif yang dihitung P^calc didapat dari persamaan berikut :

calc                  calccalc

^(Pk   )  = Vrk ⁽Irk )  ⁺ Vmk ⁽Imk )

calc                  calccalc

⁽Qk  )  — Vrk ⁽Irk  )  ^- Vmk ⁽Imk )

Dengan nilai dari masing-masing a_k , b_k , c_k , dan

dk didapat dari persamaan berikut :

„   Qk (Vrl - Kk ) - 2 VrkVmkPk

ak                V 4                - (9)

h _ PkVrI - Kk ) + 2 VrkVmkQk

bk —               V4                  ... (10)

C k —- bk .................................... (11)

dk — ak     .................................... (12)

Dari persamaan diatas, maka persamaan arus injeksi bisa dirumuskan sebagai berikut :

_— Vrk ∆Pk + Vmk ∆ Qk (Vrk )2 + (Vmk )2

_— Vmk ∆Pk + Vrk ∆ Qk (Vrk )2 + (Vmk )2

Dengan nilai tegangan V^ — V_rk + V_mm_k

(18)

(19)

Matriks admitansi tersebut nantinya digunakan untuk menghitung besarnya injeksi arus yang harus diberikan pada masing-masing bus (Garcia, 2000).

2.3 . Koreksi Tegangan Bus

Koreksi tegangan bus pada koordinat kutub, dengan iterasi umum (h+1) adalah :

Vk^h+1 — Vk^h + ∆ Vk^h

θk^h+1 = θk^h + ∆θk^h

∆ Vk = V^l ∆ Vrk + Vmt ∆ V_mk

Vrk         Vmk

^∆θk = v 2 ^δ Vmk   v 2 ^δ Vrk

Persamaan di atas adalah linearisasi dari :

θ_k = tan ^-1 V^mk-^k

rk

Fitur penting pada formula Injeksi Arus adalah sebagian besar dari blok (2 x 2) matriks Jacobian tanpa perubahan selama proses. Diagonal blok (2 x 2), mempunyai spesifik beban selain dari beban impedansi, harus di-update pada setiap iterasi (da Costa, 1999).

• 2.4    Flowchart Metode Injeksi Arus

Flow chart metode injeksi arus seperti dibawah

ini:

• 3.    METODOLOGI

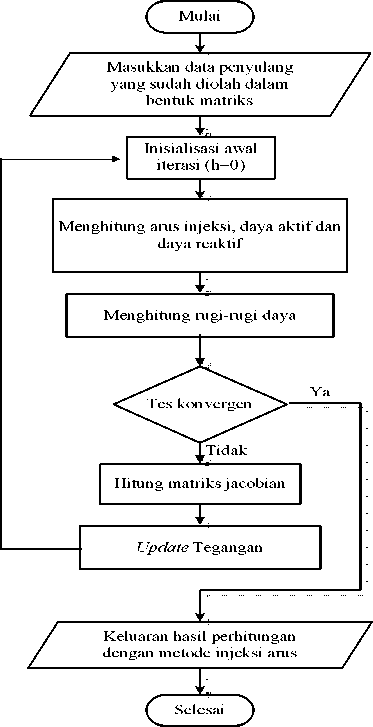
Data-data yang digunakan bersumber dari PT PLN ( Persero ) Area Jaringan Bali Timur. Analisis data menggunakan program MATLAB Versi 6.5.1.

• 3.1    Komponen Penyulang

Komponen penyulang merupakan bagian terpenting dalam melakukan analisa aliran daya. Adapun komponen yang digunakan dalam melakukan analisa aliran daya adalah :

• 1.    Single-line diagram penyulang

• 2.    Data daya aktif dan reaktif pada bus beban

• 3.    Kapasitas trafo distribusi

• 4.    Data penghantar

Bila data yang diperlukan tidak tersedia, maka diperlukan asumsi-asumsi dengan memperhatikan kondisi yang ada.

Tabel 1. Data Penghantar

No	Jenis Penghantar	R (ohm/km)	X (ohm/km)
1	Kabel tanah XPLE	0,159	0,105
2	MVTIC 150 mm2	0,265	0,106
3	A3COC 150 mm2	0,236	0,300
4	A3C 150 mm2	0,236	0,300
5	A3C 95 mm2	0,374	0,332
6	A3C 70 mm2	0,503	0,341

Sumber : PT PLN (Persero) Area Jaringan Bali Timur

• 3.2    Penyulang Tenganan

Penyulang Tenganan adalah penyulang dari Gardu Induk (GI) Amlapura dengan kapasitas trafo 20 MVA, memiliki 37 trafo distribusi dengan kapasitas total 4465 kVA. Dengan daya aktif (P) = 3795.25 kW dan daya reaktif (Q) = 2366.45 kVAR.

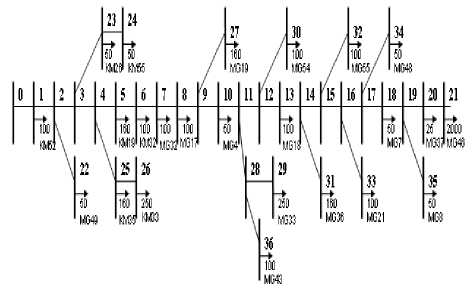
Gambar 5.1 Single-line diagram penyulang Tenganan

• 3.3    Penyulang Bukit Jati

Penyulang Bukit Jati adalah penyulang dari Gardu Induk Gianyar trafo 20 MVA, memiliki 25 trafo distribusi dengan kapasitas total 2335 kVA. Dengan daya aktif (P) = 1984.75 kW dan daya reaktif (Q) = 1237.55 kVAR.

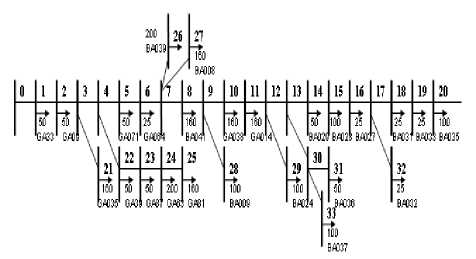
Gambar 5.2 Single-line diagram penyulang Bukit Jati

• 3.4    Penyulang VIP 2

Penyulang VIP 2 adalah penyulang dari Gardu Induk Sanur dengan kapasitas trafo 60 MVA, dan memiliki 19 trafo distribusi dengan kapasitas total 9530 kVA. Dengan daya aktif (P) = 8291.1 kW dan daya reaktif (Q) = 5146.2 kVAR.

O

1

5

5

4

5

O

S

P

10

11

1!

13

14

15

Id

1'

13

IP

→

111

Hi

-4

511

m

«1

Bl

Kl

ill

til own

ill DTi

on

ill DB

DKlT

Bl Olli!

DlIM

Bl dibs

oma

«1 Dlil

OWT

H OlBJ

OlM

mi Olffl

401 DE24

DllM

«si OlW

OlBl

ill Oias

Gambar 5.3 Single-line diagram penyulang VIP 2

• 4.    ANALISA ALIRAN DAYA PADA PENYULANG 20 KV DI BALI

  • 4.1    Penyulang Tenganan

Dengan menggunakan simulasi program.

Tabel 2. Perbandingan Hasil Analisa Tegangan Penyulang Tenganan

Bus	Injeksi Arus (kV)	Newton-Raphson (kV)
Swing bus	20.0000	20.0000
Bus 1	19.8351	19.6862
Bus 2	19.8266	19.6724
Bus 3	19.7998	19.6255
Bus 4	19.5365	19.1566
Bus 5	19.5255	19.1300
Bus 6	19.5184	19.1137
Bus 7	19.5108	19.0846
Bus 8	19.5066	19.0691
Bus 9	19.5025	19.0541
Bus 10	19.4936	19.0229
Bus 11	19.4929	19.0203
Bus 12	19.4773	18.9484
Bus 13	19.4765	18.9439

Bus 14	19.4757	18.9397
Bus 15	19.4739	18.9272
Bus 16	19.4657	18.8686
Bus 17	19.4635	18.8416
Bus 18	19.4632	18.8371
Bus 19	19.4629	18.8064
Bus 20	19.4628	18.7863
Bus 21	19.4626	18.7756
Bus 22	19.8209	19.6708
Bus 23	19.7991	19.6245
Bus 24	19.7990	19.6244
Bus 25	19.5352	19.1535
Bus 26	19.5345	19.1525
Bus 27	19.5025	19.0530
Bus 28	19.4920	19.0181
Bus 29	19.4920	19.0180
Bus 30	19.4771	18.9482
Bus 31	19.4757	18.9396
Bus 32	19.4736	18.9261
Bus 33	19.4656	18.8681
Bus 34	19.4633	18.8413
Bus 35	19.4629	18.8063
Bus 36	19.4917	19.0179

Berdasarkan tabel 2, dapat dilihat bahwa hasil tegangan pada metode Injeksi Arus lebih stabil dibandingkan dengan hasil tegangan pada metode Newton-Raphson. Metode Injeksi Arus memiliki tegangan terkecil pada bus 21 dengan besar tegangan 19.4626 kV, dengan penurunan tegangan= 2,687 %.

Sedangkan tegangan terkecil dengan metode Newton-Raphson terletak pada bus 21 dengan besar tegangan 18.7756 kV, sedangkan penurunan tegangannya = 6,122 %. Untuk sistem radial drop tegangan yang diijinkan adalah sebesar 5 % dari tegangan kerja (SPLN 72, 1987).

Hal ini berarti drop tegangan harus lebih kecil atau sama dengan 1 kilo volt, dan tegangan yang sesuai standar adalah sama dengan atau lebih dari 19 kilo volt. Berdasarkan tabel 4.11 diatas, maka tegangan pada bus 12, bus 13, bus 14, bus 15, bus 16, bus 17, bus 18, bus 19, bus 20, bus 21, bus 30, bus 31, bus 32, bus 33, bus 34, dan bus 35 pada hasil analisa dengan metode Newton-Raphson berada dibawah standar yang diijinkan PLN.

• 4.2    Penyulang Bukit Jati

Dengan menggunakan simulasi program. Hasil analisa dapat dilihat pada tabel 3 berikut :

Tabel 3. Perbandingan Hasil Analisa Tegangan Penyulang Bukit Jati

Bus	Injeksi Arus (kV)	Newton-Raphson (kV)
Swing bus	20.0000	20.0000
Bus 1	19.9081	19.8581
Bus 2	19.8893	19.8296
Bus 3	19.8698	19.8002
Bus 4	19.8677	19.7970
Bus 5	19.8667	19.7955
Bus 6	19.8621	19.7887
Bus 7	19.8382	19.7544
Bus 8	19.8327	19.7473
Bus 9	19.8253	19.7390
Bus 10	19.7950	19.7038
Bus 11	19.7716	19.6787
Bus 12	19.7192	19.6328
Bus 13	19.7164	19.6306
Bus 14	19.7143	19.6293
Bus 15	19.7027	19.6221
Bus 16	19.6943	19.6178
Bus 17	19.6836	19.6110
Bus 18	19.6831	19.6106
Bus 19	19.6787	19.6080
Bus 20	19.6770	19.6066
Bus 21	19.8679	19.7976
Bus 22	19.8657	19.7926
Bus 23	19.8652	19.7903
Bus 24	19.8645	19.7855
Bus 25	19.8637	19.7829
Bus 26	19.8382	19.7507
Bus 27	19.8382	19.7531
Bus 28	19.8252	19.7388
Bus 29	19.7191	19.6325
Bus 30	19.7140	19.6279
Bus 31	19.7137	19.6270
Bus 32	19.6837	19.6108

Berdasarkan tabel 3, dapat bahwa hasil tegangan pada metode Injeksi Arus lebih stabil dibandingkan dengan hasil tegangan pada metode Newton-Raphson. Metode Injeksi Arus memiliki tegangan terkecil pada bus 20 dengan besar tegangan 19,677 kV, dengan penurunan tegangan= 1.61 %. Sedangkan tegangan terkecil dengan metode Newton-Raphson terletak pada bus 20 dengan besar tegangan 19.6066 kV, sedangkan penurunan tegangannya = 1.967 %.

• 4.3    Penyulang VIP 2

Hasil analisa dapat dilihat pada tabel 4

Tabel 4. Perbandingan Hasil Analisa Tegangan Penyulang

Bukit Jati

Bus	Injeksi Arus (kV)	Newton-Raphson (kV)
Swing bus	20.0000	20.0000
Bus 1	19.9493	19.8905
Bus 2	19.8873	19.7729
Bus 3	19.8790	19.7570
Bus 4	19.8708	19.7408
Bus 5	19.8569	19.7130
Bus 6	19.8434	19.6862
Bus 7	19.8376	19.6749
Bus 8	19.8303	19.6611
Bus 9	19.8256	19.6522
Bus 10	19.8167	19.6321
Bus 11	19.7862	19.5568
Bus 12	19.7757	19.5306
Bus 13	19.7686	19.5134
Bus 14	19.7647	19.5032
Bus 15	19.7616	19.4965
Bus 16	19.7580	19.4847
Bus 17	19.7542	19.4726
Bus 18	19.7530	19.4675
Bus 19	19.7525	19.4664

Berdasarkan tabel 4, dapat disimpulkan bahwa hasil tegangan pada metode Injeksi Arus lebih tinggi pada setiap bus-nya dibandingkan dengan hasil tegangan pada metode Newton-Raphson. Metode Injeksi Arus memiliki tegangan terkecil pada bus 19 dengan besar tegangan 19.7525 kV, dengan penurunan tegangan= 1.23 %. Sedangkan tegangan terkecil dengan metode Newton-Raphson terletak pada bus 19 dengan besar tegangan 19.4664 kV, sedangkan penurunan tegangannya = 2.67 %.

• 4.4    Perbandingan Hasil Analisa Pada Masing-
  
  Masing Penyulang

Berdasarkan hasil analisa dari masing-masing penyulang, maka dapat dibandingkan kecepatan dan jumlah iterasi yang dilakukan metode Injeksi Arus dan metode Newton-Raphson untuk melakukan analisa.

Tabel 5. Perbandingan Hasil Analisa Pada Masing-Masing Penyulang

Metode Analisa Daya	Waktu	Jumlah Iterasi
Penyulang Tenganan
Injeksi Arus	0.078 detik	1
Newton-Raphson	0.422 detik	1
Penyulang Bukit Jati
Injeksi Arus	0.063 detik	1
Newton-Raphson	0.157 detik	1
Penyulang VIP 2
Injeksi Arus	0.015 detik	1
Newton-Raphson	0.25 detik	2

Dari tabel 5, dapat dilihat bahwa metode Injeksi Arus lebih cepat dalam melakukan analisa aliran daya dibandingkan dengan metode Newton-Raphson. Sedangkan jumlah iterasi yang dilakukan untuk mencapai konvergen, metode Injeksi Arus lebih baik dibandingkan metode Newton-Raphson karena pada penyulang VIP 2, metode Newton-Raphson melakukan 2 iterasi untuk mencapai nilai yang konvergen sedangkan metode Injeksi Arus memerlukan 1 iterasi untuk mencapai konvergen.

• 5.    SIMPULAN

Berdasarkan analisa yang dilakukan, maka dapat disimpulkan bahwa :

• 1.    Hasil analisa tegangan dengan metode injeksi arus pada masing-masing penyulang memiliki hasil yang lebih tinggi dibandingkan dengan hasil analisa dengan metode Newton-Raphson. Hal ini dapat dilihat dari nilai tegangan terkecil dari masing-masing penyulang. Hasil analisa metode injeksi arus pada penyulang Tenganan tegangan terkecil terdapat pada bus 21 yaitu 19.4626 kV, sedangkan dengan metode Newton-Raphson tegangan terkecil juga terdapat pada bus 21 yaitu 18.7756 kV. Pada penyulang Bukit Jati, tegangan terkecil hasil metode injeksi arus terdapat pada bus 20 yaitu 19,677 kV, sedangkan pada metode Newton-Raphson tegangan terkecil terdapat pada bus 20 yaitu 19.6066 kV. Pada penyulang VIP 2, tegangan terkecil hasil metode injeksi arus terdapat pada bus 19 yaitu 19.7525 kV, sedangkan pada metode Newton-Raphson tegangan terkecil terdapat pada bus 19 yaitu 19.4664 kV.

• 2.    Metode Injeksi Arus memerlukan waktu yang lebih sedikit untuk melakukan iterasi dibandingkan dengan metode Newton-Raphson.

• 3.    Pada kondisi sistem radial yang linier (tidak bercabang) yaitu pada penyulang VIP 2, metode Injeksi Arus lebih efisien dibandingkan metode Newton-Raphson. Hal ini terbukti dengan jumlah iterasi   yang   dilakukan  untuk mencapai

konvergen. Dengan metode Injeksi Arus, proses iterasi yang diperlukan sebanyak 1 kali sedangkan dengan metode Newton-Raphson proses iterasi sebanyak 2 kali untuk mencapai nilai konvergen.

• 6.    DAFTAR PUSTAKA

• [1] . Beaty, H.W. 2001. Handbook of Electric Power Calculations – Third Edition . New York : McGraw-Hill.

• [2] . Chen, T.H, Chen, M.S, Hwang, K.J, Kotas, P, Chebli, E.A. 1991. Distribution System Power Flow Analysis – A Rigid Approach. IEEE Transactions on Power Delivery, Vol. 6, No. 3.

• [4] . Da Costa, V.M, Martins, N, Pereira, J.L.R. 1999. Developments in the Newton-Raphson Power Flow Formulation Based on Current Injections. IEEE Transactions on Power Systems, Vol. 14, No. 4.

• [5] . Davis, C.E. 1997. IEEE Recommended Practice for Industrial and Commercial Power Systems Analysis – Chapter 6. Load Flow Studies. New York, USA : The Institute of Electrical and Electronics Engineering, Inc.

• [6] . Garcia, P.A.N, Pereira, J.L.R, Caneiro, S.Jr, da Costa, V.M, Martins, N. 2000. Three-Phase Power Flow Calculations Using The Current Injection Method. IEEE Transactions On Power System, vol. 15, No. 2.

• [7] . Khodr, H.M. 2006. New Load Flow Method S-E Oriented For Large Radial Distribution Networks. IEEE PES Transmission and Distribution Conference and Exposition Latin America, Venezuela

• [8] . Stevenson,Jr. dan William, D. 1990. Analisis Sistem Tenaga Listrik. Bandung : Erlangga.

• [9] . Venkatesh, B.2003 Data structure for radial distribution system load flow analysis. IEEE Proc. Gener. Trans. Distrib. Vol 150. no 1.

• [10] . Zimmerman, R.D. 1992. Network Reconfi guration For Loss Reduction In Three-Phase Power Distribution Systems. New York : Cornell University.

• [11] . ______. 1987. SPLN 72 : Spesifikasi Desain

Untuk Jaringan Tegangan Menengah (JTM) dan Jaringan Tegangan Rendah. Jakarta : Departemen Pertambangan dan Energi Perusahaan Umum Listrik Negara.

Teknologi Elektro

51

Vol. 8 No. 1 Januari - Juli 2009