New Orthogonal Small Set Kasami Code Sequence

PRAMAITA et.all: NEW ORTHOGONAL SMALL SET KASAMI CODE SEQUENCE 2015

47

New Orthogonal Small Set Kasami Code Sequence

Nyoman Pramaita, IGAGK Diafari DH, Dewa NK Putra Negara, and Agus Dharma

Abstract— In this paper, the authors propose the design of a new orthogonal small set Kasami code sequence generated using combination of non-orthogonal m-sequence and small set Kasami code sequence. The authors demonstrate that the proposed code sequence has comparable auto-correlation function (ACF), crosscorrelation function (CCF), peak cross-correlation values with that of the existing orthogonal small set Kasami code sequence. Though the proposed code sequence has less code sequence sets than that of the existing orthogonal small set Kasami code sequence, the proposed code sequence possesses one more numbers of members in each code sequence set. The members of the same code set of the proposed code sequence are orthogonal to each other.

Index Terms—ACF, CCF, orthogonal code, spreading code

• I.    Introduction

Binary spreading code sequence can be divided into two categories, i.e. orthogonal and non-orthogonal code sequences. Each of these spreading code sequences has its own unique parameter including autocorrelation, cross-correlation, and family size or number of different spreading code sequences in a chip set [1].

When the cross-correlation value between any two spreading code sequences from same chip set is not zero, spreading code sequences in that chip set are called non-orthogonal code sequences. While orthogonal code sequences have zero cross-correlation value between any two spreading code sequences from same chip set [2].

Maximal-sequence (m-sequence), Gold and Kasami code sequences (three families of binary spreading code sequences) have established themselves as popular non-orthogonal binary code sequences. Walsh code sequence, which is generated by mapping code word rows of special square matrices called Hadamard matrices has proven its existence as a popular

Nyoman Pramaita is a lecturer in Electrical Engineering, Faculty of Technology, Udayana University (e-mail: [email protected]).

IGAGK Diafari DH is a lecturer in Electrical Engineering, Faculty of Technology, Udayana University (e-mail: [email protected]).

Dewa Ngakan Ketut Putra Negara is a lecturer in Mechanical Engineering, Faculty of Technology, Udayana University (e-mail: [email protected] ).

Agus Dharma is a lecturer in Electrical Engineering, Faculty of Technology, Udayana University (e-mail: [email protected]).

orthogonal code sequence [3], [4]. However, orthogonal Gold code sequence, orthogonal m-sequence, and orthogonal small set Kasami code sequence are orthogonal code sequences generated from their non-orthogonal counter parts [5]-[7].

Walsh code sequence, orthogonal Gold code sequence and orthogonal m-sequence have numbers of members in a code set which are the same as the length of the orthogonal code sequences. However, numbers of members in a code set of the existing orthogonal small set Kasami code sequence proposed by Chandra and Chattopadhyay [6] are less than that of the chips length.

In this paper, hybrid method that is combination of non-orthogonal m-sequence and small set Kasami code sequence is proposed to generate orthogonal code sequences having number of orthogonal code sequences are the same as the length of the orthogonal code sequences.

Evaluation of the proposed code sequence includes evaluating their performance metrics such as autocorrelation function (ACF), cross-correlation function (CCF), correlation margin (CM), and merit factor (MF).

• II.    Maximal length and non-orthogonal small set Kasami code sequences

• A.    Maximal Length Sequence

Maximal-length sequence is a form of pseudo noise (PN) sequence. Pseudo noise sequence is a periodic binary sequence with a noise-like waveform that is generated by using a linear feedback shift register [8], [2]. The period of a PN sequence produced by a linear feedback shift register of length n cannot exceed the value . When the period is exactly , the PN sequence is called a maximal-length sequence or simply m-sequence [9]. There is no standard formula for the family size of m-sequence.

• B.    Small Set Kasami Code Sequence

Small set Kasami code sequence is a non-orthogonal code sequence and generated from m-sequence by using a set of algorithms as explained below.

Let u be an m-sequence of length N generated by a generator polynomial of degree n, and let w be a code sequence obtained by decimating u by + 1, where n is an even number and . Then, the code sequence w is also an m-sequence of length – 1. The small set Kasami

code sequence is then given by [6]:

K_s = (u,uφu', u&Tw,..., u® T’²"'^1-2 w)         (1)

where K_s is a small set Kasami code sequence of length N= 2^π -1; T denotes cyclic shift operator; ® denotes XOR operation, and 2"'² - 'L is the shift parameter for w. Since w and u have different code sequence lengths, we must first perform N/(2ⁿⁱ² - ¹) repetitions of the code sequence w before performing the XOR operation.

These code sequences have a family size (M) of ^: binary code sequences, each of length JV = 2^r' - 1.

• C.    Orthogonal small set Kasami code sequence

Orthogonal small set Kasami code sequences are generated from non-orthogonal small set Kasami code sequence using the set of algorithms presented in the flowchart shown in fig. 1 [6].

Orthogonal small set Kasami code sequence is capable to produce (√V7ι) n number of distinct code sequences, each of length N + 1 chips, where √jvTι is number of code sequence sets and N is number of members in each code sequence set. Peak cross-correlation value of this code sequence is N +1 , whereN= 2^r, -1for any even number n.

• III.    design of new orthogonal small set kasami code sequence

The method used by Donelan and O’Farrell [7] in generating orthogonal m-sequence has been adapted to design the proposed code sequence in this paper.

Let small set Kasami code sequence and m-sequence, each of length N(N= 2" -1 for n is an even number) and generated using the same generator polynomial, be represented by [k₁} and {u_l) respectively. These two code sequences can be represented as:

CfcfJ-A — ^^,β^J — T^C {k^, f<γ, l<2 >.. ._l ky—2' k∖f-γ)           (2)

{u_l}_c = 7^β{u_i}= T^eGlfUi-Mj*" ∙∙^uM-2^uN-l^        (3)

Where G= (0,1,Z,...,/V-D denotes shift parameter; V^c{fc_l} and r^β{u_i] represent cyclic shift of small set Kasami code sequence and m-sequence respectively.

CfcjJ and Itifl as in (2) and (3) are binary digits. By replacing bit 0 by 1 and bit 1 by -1, hybrid code sequences are obtained by multiplying the small set Kasami code sequence with all resulting m-sequence shifted by one chip. This is expressed mathematically as below:

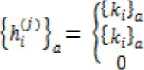
× 7^{u_j}_β

f or 0 ≤ J < JV for j = N otherwise

(4)

where T>tu_l}_a represents a cyclic shift of ^^aJc by j chips. As can be seen in (4), ^i ^c for j =N is the original small set

Kasami code sequence.

The following steps describe the procedure to convert the hybrid code sequences resulting from (4) to be a set of orthogonal code sequences [7]:

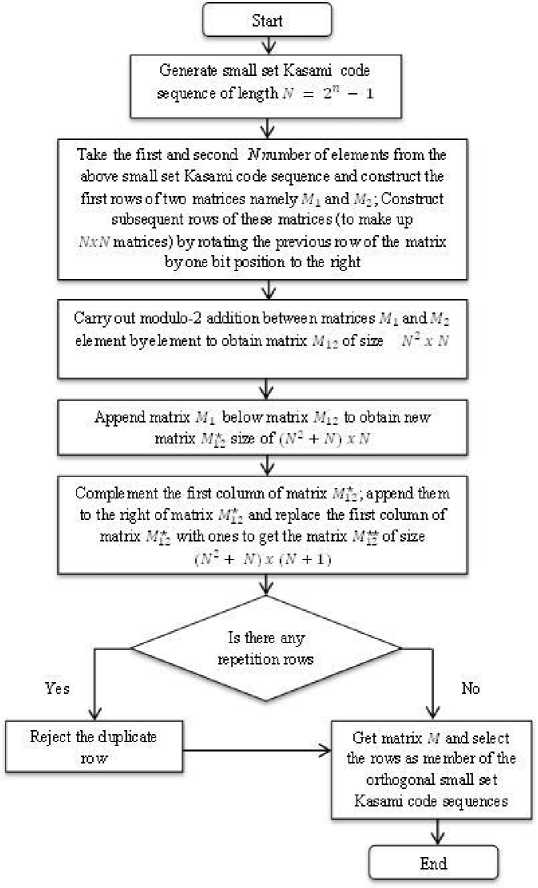
Fig. 1. Algorithm for generation of orthogonal small set Kasami code sequences

Step 1: replace the first column (the first chips) by ‘1s’.

Step 2: if the first chips were already all ‘1s’ and therefore have not been altered by step 1 then append ‘-1s’ at the end of the code sequences (column).

Step 3: if the first chip were all ‘-1s’and therefore have been altered by step 1 then append ‘1s’ at the end of the code sequences.

Step 4: repeat step 1 to 3 for all the code sequences represented in (4).

These steps in obtaining the proposed orthogonal code sequence can be mathematically represented as below:

(°^ωL= (^ιω* (^sωL'(-⅛^j∖)

(5)

where {^s^} is the resulting I h t^J I matrix with the first chip (column) (^Q⁷ ) removed. The set of code sequence

• - S

{°¾ is a set of code sequences of(JV + 1X(N+1] matrix whose rows are orthogonal to each other.

Each value of ‘a’ in (2) and (3), by the process explained above i.e. applying equation (4) and (5), generates one set of orthogonal code sequence. Therefore, one set of orthogonal code sequence will be generated for each value of ‘a’ using this process. As a result, there will be N sets of orthogonal code sequences.

However, since the code sequence W' must be first repeated N∕(2^nf2 - IJ times before performing the XOR operation as explained in section 2, there are N∕(2ⁿ^ - IJ identical sets of orthogonal code sequences. Therefore, combination of m-sequence and the small set Kasami code sequence generates (2"^z2 - 1) different sets of orthogonal code sequences.

• IV.    Results and Discussion

In the following section, the performance metrics of the proposed code sequence simulated using Matlab programming is compared to that of the existing orthogonal small set Kasami code sequence.

• A.    Capacity and Peak Cross-correlation of the Proposed Code Sequence

Let numbers of registers, n is equal to 6 then value of N is equal to 63 to evaluate the performance metrics of the proposed code sequence.

The proposed code sequence has less code sequence sets than that of orthogonal small set Kasami code sequence as shown in table 1. However, the proposed code sequence possesses one more numbers of members in each code set. These members of the same code set are orthogonal to each other.

. A set of codes are said to be orthogonal when the crosscorrelation is zero between any two members of the same code set. However, this does not mean that any member in a group of codes should also be orthogonal to other members in other groups. In a synchronous CDMA system this ensures that there is no interference between signals transmitted by the same station. These sets can be used simultaneously if the peak cross-correlation value between the code sequences (from different groups) is less than half of the code sequence length [7]. Since the peak cross-correlation value of the proposed code sequence of length 64 chips is 8, which is one eighth of 64, 7 groups of the proposed code sequence can be used simultaneously. This means, this code sequence set could

support 7 different cells in a synchronous CDMA system.

• B.    Autocorrelation Function of The proposed Code

Sequence

Autocorrelation function of the proposed code sequence and orthogonal small set code sequence for 64 chip lengths are presented in fig. 2 and fig. 3 respectively. As seen in the fig. 2 and fig. 3, at zero time shifts the orthogonal code sequences have maximum autocorrelation values since the values were obtained from correlation between code sequence with a copy of its self that has the same chips structure as the original one. However, at non-zero time shifts, the autocorrelation values are not maximum due to different chips structure between two code sequences.

TABEL 1

CAPACITY AND PEAK CROSS-CORRELATION OF THE PROPOSED

CODE SEQUENCES

Orthogonal code sequence	Length of code sequence (chips)	Number of sets	Number of members (codes)	Capacity of code sequence (users)	Peak crosscorrelation value
The proposed	64	7	64	448	8
code Orthogonal small set	64	8	63	504	8
Kasami

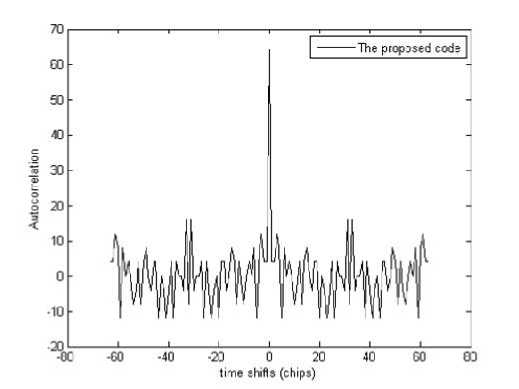
Fig. 2. ACF of the proposed code sequence

Based on these autocorrelation functions, merit factor (MF) of the proposed code sequence and orthogonal small set code sequence is tabulated in table 2.

Since MFs of these orthogonal code sequences are similar, the proposed code sequence has autocorrelation function values comparable to that of the existing orthogonal small set code sequence.

TABEL 2 MF OF THE PROPOSED CODE SEQUENCE
Orthogonal code sequence	Length of code sequence (chips)	MF
The proposed code	64	0.66
Orthogonal small set	64	0.54
Kasami

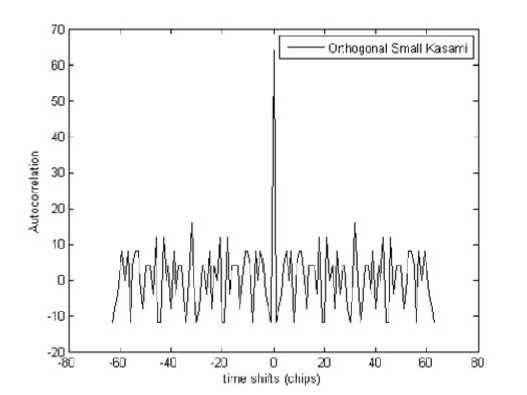
Fig. 3. ACF of the existing orthogonal small set Kasami code sequence

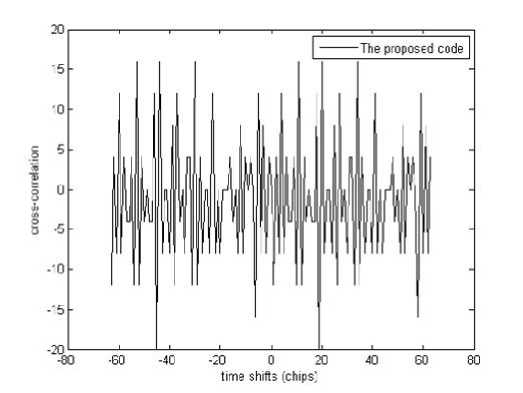
Fig. 4. CCF of the proposed code sequence

• C.    Cross-correlation Function of The proposed Code

Sequence

As seen in the fig. 4 and fig. 5, cross-correlation values of the orthogonal code sequences at zero time shifts are zeros since orthogonal code sequence means code sequence having zero cross-correlation value at zero time shift. However, some cross-correlation values are not zero at non-zero time shifts since the chips structure of the orthogonal code sequence has been changed when the orthogonal code sequence was shifted.

Based on these cross-correlation functions, correlation margin (CM) of the proposed code sequence and orthogonal small set Kasami code sequence for 64 chip lengths is tabulated in table 3.

As seen in table 3, the proposed code sequence has similar CM to that of orthogonal small set Kasami code sequence. Therefore, in terms of CM, the proposed code sequence has similar CCF to that of orthogonal small set Kasami code sequence.

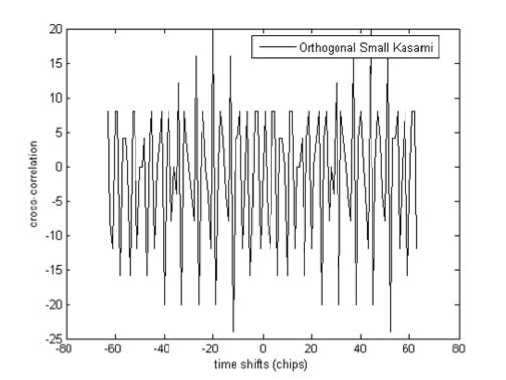
Fig. 5. CCF of the existing orthogonal small set Kasami code sequence

TABEL 3 CM OF THE PROPOSED CODE SEQUENCE
Orthogonal code sequence	Length of code sequence (chips)	CM (dB)
The proposed code	64	-12.04
Orthogonal small set Kasami	64	-12.04

• V. Conclusion

In this paper, the design of new orthogonal small set Kasami code sequence has been proposed and evaluated. The ACF, CCF and peak cross-correlation of the proposed code sequence have been shown to be similar to that of the existing orthogonal small set Kasami code. Though the existing orthogonal small set Kasami code sequence has more numbers of orthogonal code sets than that of the proposed code, the numbers of orthogonal code sequences in each code set are less than that of the chip lengths. However, designing

orthogonal small set Kasami code sequence using combination of m-sequence and non-orthogonal small set Kasami code sequence can generate orthogonal codes having numbers of orthogonal codes are the same as the length of the code. Therefore, this hybrid method can generate more numbers of orthogonal code sequences in each code set than that of the existing small set Kasami code sequence.

References

• [1]    Mollah, M.B. and Islam, Md.R. (2012) ‘Comparative analysis of Gold codes with PN codes using correlation property in CDMA technology’, IEEE International Conference on Computer Communication and Informatics (ICCCI), pp.1-6

• [2]    Ziani, A. and Medouri, A. (2012) ‘Analysis of different pseudo-random and orthogonal spreading sequences in DS-CDMA’, IEEE International Conference on Multimedia Computing and Systems (ICMCS), pp.558564.

• [3]    Pal, M. and Chattopadhyay, S. (2010) ‘A novel orthogonal minimum cross-correlation spreading code in CDMA system’, IEEE International Conference on Emerging Trends in Robotics and Communication Technologies, pp.80-84.

• [4]    Dinan, E.H. and Jabbari, B (1998) ‘Spreading codes for direct sequence CDMA and wideband CDMA cellular networks’, IEEE Communication Magazine, Vol. 36, pp.48-54.

• [5]    Tachikawa, S. (1992) ‘Recent spreading codes for spread spectrum communication systems’, Electron. Commun. Jpn., pp. 4149.

• [6]    Chandra, A. and Chattopadhyay, S. (2009) ‘Small set orthogonal Kasami codes for CDMA system’, 4th IEEE International Conference on Computers and Devices for Communication, pp.1-4.

• [7]    Donelan, H. and O’Farrell, T. (1999) ‘Method for generating sets of orthogonal sequences’, Electronic Letters, Vol. 35.

• [8]    Lee, J.S. and Miller, L.E. (1998) CDMA system engineering hand book, Artech House.

• [9]    Xinyu, Z. (2011) ‘Analysis of m-sequence and Gold sequence in CDMA system’, IEEE 3rd International Conference on Communication Software and Networks (ICCSN)’, pp. 466-468

1693-2951©2015 JTE