Analisis Dan Implementasi Metode Steepest Descent Untuk Mengurangi Blur Pada Citra Digital
on
Analisis dan Implementasi Metode Steepest Descent
I Gede Adnyana
ANALISIS DAN IMPLEMENTASI METODE STEEPEST DESCENT UNTUK MENGURANGI BLUR PADA CITRA DIGITAL
I Gede Adnyana
Program Magister (S2) Teknik Elektro, Pascasarjana
Universitas Udayana, Denpasar, Bali adnyana.nakkuta@gmail.com
Abstrak
Seringkali dalam pengambilan suatu objek tertentu hasil citra yang didapat mengalami degradasi atau penurunan kualitas citra, salah satunya terjadinya blur yang diakibatkan oleh kamera yang tidak fokus dalam menangkap suatu objek. Oleh karena itu diperlukan perbaikan untuk citra yang terdegradasi tersebut, dalam hal ini digunakan metode Steepest Descent dalam proses pengurangan blur. Ide dasar metode ini adalah melakukan iterasi untuk mengurangi blur dengan menelusuri titik yang paling curam. Blur yang dimasukkan pada citra digital adalah Gaussian dan Motion blur yang dibangkitkan melalui suatu blur generator. Performansi yang diujikan adalah PSNR (Peak Signal to Noise Ratio) dan Similarity citra hasil pengurangan blur. Dari hasil analisis didapatkan bahwa secara umum metode Steepest Descent dapat digunakan untuk mengurangi blur, namun kurang handal mengurangi blur dengan intensitas tinggi karena menghasilkan citra dengan PSNR kurang dari 30 dB dan Similarity yang meningkat.
Kata kunci: Blur, Steepest Descent, Similarity, Gaussian Blur, Motion Blur
-
1. PENDAHULUAN
Citra digital sebagai salah satu media untuk mendokumentasikan suatu momen, makin banyak diminati orang. Citra digital memiliki kelebihan, salah satunya adalah kepraktisan dalam mendapat hasil cetakan dibandingkan citra analog.
Kamera digital sebagai sarana dalam pengambilan citra digital pun sekarang telah banyak tersedia dengan beraneka ragam jenis. Kamera yang ada saat ini mampu menangkap gambar dan mempresentasikannya menjadi bentuk citra digital ternyata memiliki berbagai kekurangan dalam menangkap keadaan secara akurat. Misalnya saja terjadi keterbatasan dalam resolusi gambar yang dihasilkan atau juga keterbatasan kecepatan pada saat menangkap gambar. Keterbatasan tersebut tentunya dapat membuat citra hasilnya terdegradasi. Degradasi yang sering terdapat pada citra hasil tersebut adalah terjadinya blur dan noise.
Pada kehidupan nyata efek blur pada citra digital dapat terjadi jika kamera tidak terlalu fokus pada objek yang akan ditangkap gambarnya. Misalnya ketika kita ingin menangkap objek yang bergerak dengan kamera, sering kali kita mendapat hasil citra yang blur.
Oleh karena itu diperlukan metode-metode untuk memperbaiki citra digital yang terdegradasi agar citra yang dihasilkan dapat menjadi lebih jelas. Perbaikan citra, khususnya pengurangan blur pada citra adalah suatu langkah untuk mendapatkan citra yang lebih jelas dari citra yang terdegradasi dengan hanya mengetahui beberapa faktor degradasi dari citra tersebut. Dalam penelitian ini penulis menerapkan metode Steepest Descent untuk mengurangi blur. Ide dasarnya adalah melakukan iterasi untuk mengurangi blur dengan menelusuri titik yang paling curam.
-
2. PENGOLAHAN CITRA
Istilah pemrosesan citra digital secara umum mengarah pada pemrosesan gambar dua dimensi oleh komputer digital. Citra digital adalah sebuah array bilangan riil atau kompleks yang dinyatakan dengan bit-bit tertentu.
Dalam bidang pengolahan citra (image processing), citra yang diolah adalah citra digital, yaitu citra kontinyu yang telah diubah ke dalam diskrit baik koordinat spasial dan tingkat keabuan.
Citra digital f( x,y ) dinyatakan sebagai sebuah matrik ( M x N ) yang indeks baris dan kolomnya megidentifikasikan sebuah titik pada citra dan elemen nilai matrik yang berupa nilai diskrit menyatakan tingkat keabuan pada titik tersebut. Citra digital yang berupa matrik dengan ukuran M x N dapat digambarkan sebagai berikut [1][2][3]
■ (0,0) ■ (0,1)
' (1,0) : (1,1)
.: (∖- 1,0) .'C. - 1,1)
f (0,M- 1) (1, <— 1)
■ ■ ■
∕('■ - 1, <- 1)
Gambar 1. Representasi Matrik Citra Digital
Blur yang coba dibangkitkan dalam penelitian ini adalah Gaussian blur dan Motion blur. Gaussian blur merupakan salah satu metode untuk mengurangi noise pada citra digital tetapi juga mengurangi detail citra tersebut. Hasil dari Gaussian blur ini membuat citra menjadi lebih halus tetapi bila terlalu besar akan menyebabkan gambar menjadi tidak jelas. Secara
matematis menambahkan Gaussian blur pada sebuah citra sama dengan melakukan konvolusi terhadap citra dengan faktor PSF Gaussian atau distribusi normal.
Gaussian blur merupakan tipe blur yang menggunakan distribusi normal (disebut juga Gaussian PSF) yang dikenai pada setiap pixel pada citra digital.
Rumus Gaussian PSF yaitu :
1 X^ y2
0=-''^- —+ - ...............(1)
Dimana σ merupakan standar deviasi dari distribusi Gaussian untuk arah x dan y. Untuk besarnya ukuran matrik ditentukan oleh ukuran dimensi matrik PSF, misalnya ukuran 3x3, 5x5 dan sebagainya. Ketika dikenai pada citra digital akan menghasilkan citra yang titik pusatnya dikenai bobot paling besar dan menyebar ke pixel tetangganya. Misalkan dilakukan pembangkitan matrik Gaussian blur 3x3 maka akan dibentuk matrik dengan ukuran 3 arah x dan ukuran 3 arah y, sehingga terbentuk matrik ukuran 3x3 dengan nilai elemen matrik didapatkan dengan persamaan (1).
Motion blur adalah efek blur yang biasanya disebabkan oleh keterbatasan kamera dalam menangkap kecepatan gambar lingkungan yang diinginkan. Untuk dapat memodelkan motion blur pada domain spasial diperlukan dua parameter utama yaitu sudut dan dimensi dari kernel atau berapa pixel pergeseran yang diinginkan [4]
Misalkan kita memiliki citra asli f yang akan didegradasi dengan PSF m=(m1, m2, m3,…., mk) dengan sudut α. Maka hasil degradasi g akan mengikuti rumus sebagai berikut :
g(x,y) =/'; * ∙,∙ι; = ∑ '*r . ■ .∖ + ∖ cos c . i + √ sin <■ …………………………………………………(2)
-
C. Tranformasi Fourier
Tranformasi fourier adalah suatu cara untuk mengubah fungsi dari spasial ke frekuensi. Untuk perubahan sebaliknya digunakan Tranformasi Fourier Balikan. Dalam citra digital Tranformasi Fourier dapat dibuat persamaan menjadi :
Fu,v= ^∑nx⅛Σ^ fx.ye~i^ u dan v =
0,1,..N-1 ………………………………………. (3)
• ux vy
fu,v= ∑uΞo∑v=oFu,υe (1^ x dan y = 0,1,..N-1
….………………………………………………. (4)
Dalam pengolahan citra digital, Tranformasi Fourier dapat digunakan dalam pembangkitan blur, dimana matrik blur dan matrik citra asli diubah terlebih dahulu ke domain frekuensi, baru kemudian dilakukan proses perkalian antara matrik blur dengan matrik citra asli. Setelah didapat hasil perkaliannya barulah digunakan Tranformasi Fourier Balikan untuk mengembalikan ke domain spasial.
-
D. Metode Steepest Descent
Dalam sistem linear diberikan persamaan Ax = b, dimana A= matrik simetrikdan definit positif (ukuran n x n), sedangkan x dan b dalam bentuk vektor (ukuran n x 1) dapat dibuat bentuk matrik sebagai berikut [5]:
Gambar 2. Matrik sistem linear Ax=b
Fungsi bentukkuadrat f(x) pada vektor ditunjukkandengan persamaan :
dimana A simetrik, x dan b vector, dan c konstanta. Bentuk kuadrat gradient f’(x) dapat didefinisikan sebagai berikut:
-∣ ω
f ∖x) =~ 'M -------------------------------------(6)
∂xn
i (*}
Berdasarkan penurunan dari persamaan (5) dan (6) didapatkan persamaan baru kuadrat gradient sebagai berikut:
f‘(x) =^<Y+ -,k - ■ > ............................(7)
Jika A simetrik maka persamaan menjadi:
f‘(x) = Ax–b …………………………………….(8)
Pada metode steepest descent menggunakan pendekatan minimum dengan memilih arah dimana f paling curam, dimana f arahnya berlawanan dengan f'(x(i)) sehingga persamaan menjadi: [6][7]
-
-f’(x(1)) = b - Ax(i) ......................................(9)
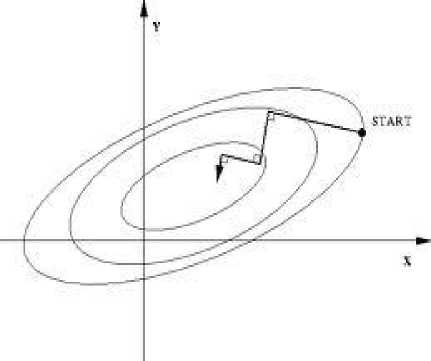
Gambar 3. Pendekatan minimum dalam langkah zigzag
metode Steepest Descent
Pada metode Steepest Descent, dimulai dengan titik x(0), x(1), x(2), … dst sampai ditemukan solusi x. Metode ini dapat dirumuskan sebagai berikut [8] [9][10][11]:
r(i) = b – Ax(i)……………………….…………(10)
= PPP), (11)
( 1 I '∣( i
x(i+1) = x(i) + ……….………….. (12)
r(i+1) = r(i)-∂i Zr⅛ .................... (13)
dimana :
= lebar langkah iterasi yang optimal dan bergantung arah r
r = arah steepest descent dari x(0) ke x(i)
Suatu citra digital yang telah terdegradasi blur dapat dimodelkan secara matematis sebagai berikut: g(x,y) = h(x,y) *f(x,y)…………………………. (14) dimana :
g(x,y) merupakan citra yang terdegradasi
h(x,y) merupakan fungsi blur
f(x,y) merupakan citra asli yang belum mengalami degradasi
Persamaan (14) dapat dianalogikan sama dengan persamaan (8). Sehingga didapatkan persamaan : Ax= b ……………………………………..…….(15) dimana :
b merupakan citra yang terdegradasi
A merupakan fungsi blur
x merupakan citra asli yang belum mengalami degradasi.
Dari karakteristik metode Steepest Descent, metode ini dapat diterapkan dalam pengurangan blur pada citra digital. Diharapkan citra hasil rekonstruksi memiliki hasil yang maksimal karena metode Steepest Descent mendeteksi dan melakukan perbaikan dengan langkah yang paling curam terhadap nilai matrik blur.
Tahapan-tahapan proses dalam sistem pengurangan blur dengan metode Steepest Descent sebagai berikut :
-
1) Proses awal yang dilakukan adalah pembacaan citra asli untuk mendapatkan matrik citra asli dan dilakukan pembentukan matrik blur. Untuk menghasilkan matrik blur, pembangkitan blur dan matrik blur tebakan berdasarkan parameter inputan user.
-
2) Selanjutnya dilakukan tranformasi ke domain frekuensi dengan menggunakan Transformasi Fourier untuk mengubah matrik citra asli dan matrik blur ke domain frekuensi.
-
3) Dilakukan proses pembentukan citra ter-blur dengan mengalikan matrik blur dengan matrik asli yang telah diubah dalam domain frekuensi.
-
4) Selanjutnya dilakukan proses Steepest Descent untuk mengurangi blur dengan tebakan awal citra digunakan citra ter-blur dan matrik blur tebakan didapatkan dari proses pembentukan matrik blur namun dilakukan proses transformasi ke domain frekuensi untuk menghasilkan matrik blur tebakan dalam domain frekuensi.
-
5) Setelah didapatkan citra hasil perbaikan, selanjutnya dilakukan proses transformasi ke domain spasial dengan Transformasi Fourier Balikan untuk mendapatkan citra perbaikan dalam domain spasial.
-
6) Selanjutnya dilakukan proses menampilkan citra hasil pengurangan blur.
Penilaian baik tidaknya citra hasil proses penghilangan blur dapat diukur dengan menggunakan parameter performansi obyektif yaitu dengan melakukan perbandingan antara citra asli dengan citra hasil pengurangan blur. Dalam penelitian ini menggunakan PSNR ( Peak Signal to Noise Ratio ) dan Similarity [11].
PSNR ( Peak Signal to Noise Ratio ) citra hasil pengurangan blur didapat dari perbandingan citra asli dengan citra hasil pengurangan blur. Citra hasil rekonstruksi jika memiliki PSNR > 30 dB. PSNR dapat dihitung menggunakan rumus:
PSNR = 10My/l(: — OR ........................(16)
Sebelumnya kita harus menghitung MSE (Mean Square Error) terlebih dahulu dengan persamaan: MSE = -τr∑⅛.∑U/ ',/ - √^))- ........(17)
Dimana:
N = panjang citra
M = lebar citra
f(x,y) = citra asli
g(x,y) = citra hasil debluring
Similarity merupakan ukuran kesamaan dua buah gambar yang dibandingkan. Matriknya dihitung berdasarkan selisih energy dari Laplacian dua buah citra yang dibagi dengan nilai Laplacian salah satu citra tersebut. Misalkan I adalah citra asli dan P adalah citra ter-blur maupun citra yang telah diproses dengan pengurangan blur. Misalkan L{I}melambangkan nilai Laplacian dari suatu citra, maka hal ini dapat dirumuskan sebagai berikut :
c I ,P
∑P∑P M ⅛‰P
∑^∑)i: ⅛}G,/)
…(18)
Semakin kecil nilai yang dihasilkan menandakan semakin sama suatu citra yang dibandingkan dengan citra aslinya. Citra yang sama akan memiliki e(I,P) sama dengan nol.
-
3. PENGUJIAN DAN ANALISIS
Dari implementasi yang telah dibuat, selanjutnya akan dilakukan pengujian pada sistem pengurangan blur. Citra yang diujikan memiliki karakteristik yang bermacam-macam. Ukuran citra yang digunakan yakni 256 x 256 dengan kedalaman warna 24 bit.
Citra yang terdegradasi Gaussian Blur akan diperbaiki menggunakan matrik tebakan Gaussian Blur. Digunakan lima sampel yang mewakili karakteristik citra yang berbeda.
Citra ter-blur yang dibangkitkan dengan Gaussian Blur direstorasi menggunakan matrik blur yang memiliki ukuran matrik yang lebih kecil dibandingkan ukuran matrik yang digunakan saat pembangkitan blur.
10--
5--
0--
1 2 3 4 5
Samael
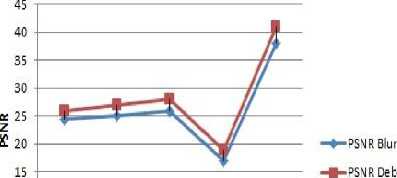
Gambar 4. Grafik perbandingan PSNR citra blur dengan citra deblur matrik 7x7 direstorasi dengan matrik 5x5
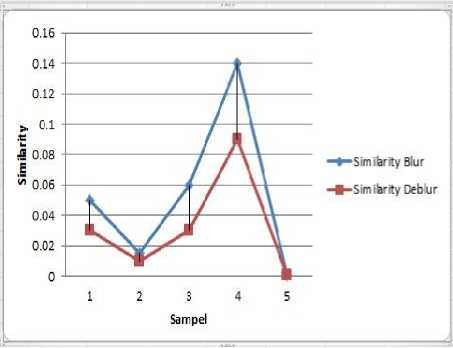
Gambar 5. Grafik perbandingan Similarity citra blur dengan citra deblur matrik 7x7 direstorasi dengan matrik 5x5
Pada gambar 4 dapat dilihat perbandingan PSNR, dimana terjadi peningkatan nilai PSNR dari citra hasil restorasi menggunakan matrik tebakan dengan ukuran lebih kecil dibandingkan matrik blur.
Begitu juga pada gambar 5 terjadi terjadi perubahan nilai similarity menjadi lebih kecil, yang berarti terjadi peningkatan kualitas citra hasil pengurangan blur. Pada pembangkitan blur, faktor yang berpengaruh terhadap kualitas blur adalah ukuran dimensi matrik pembangkit blurnya. Untuk itu perlu dianalisa bagaimana pengaruh peningkatan dimensi matrik blur terhadap nilai PSNR dan Similarity.
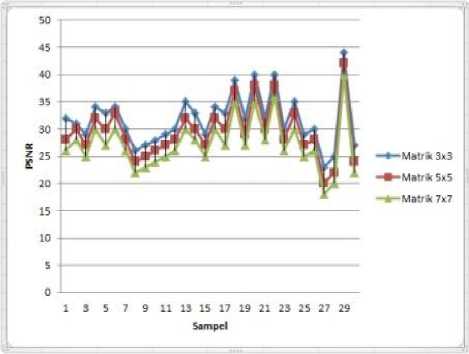
Gambar 6. Grafik perbandingan PSNR citra deblur dengan standar deviasi 30 untuk masing-masing dimensi matrik
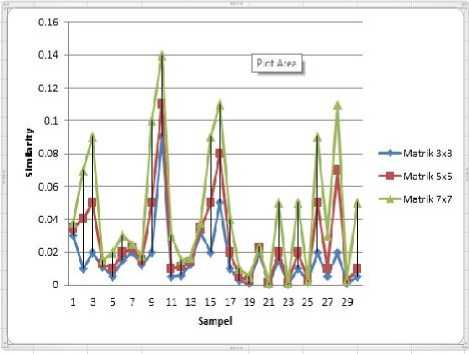
Gambar 7. Grafik perbandingan Similarity citra deblurdengan standar deviasi 30 untuk masing-masing dimensi matrik
Pada gambar 6, dapat dilihat untuk setiap sampel terjadi penurunan PSNR untuk setiap penambahan dimensi matrik. Hal serupa juga terjadi untuk nilai similarity pada gambar 7, terjadi kenaikan nilai similarity untuk setiap penambahan dimensi matrik. Jadi dapat disimpulkan bahwa semakin kuat citra terdegradasi maka pengurangan blur menggunakan metode Steepest Descentmenghasilkan penurunan nilai PSNR dan kenaikan nilai Similarity.
Selain faktor dimensi matrik blur, parameter yang menjadi inputan dalam pembangkitan blur adalah standar deviasi, namun memiliki pengaruh yang kecil terhadap PSNR dan Similarity citra hasil pengurangan blur. Hal ini disebabkan karena matrik
blur yang dibangkitkan dengan algoritma Gaussian blur dengan standar deviasi yang berbeda memiliki selisih yang sangat kecil sehingga menyebabkan citra ter-blur dengan standar deviasi yang berbeda hampir sama untuk ukuran dimensi matrik sama.
Citra blur yang dibangkitkan dengan motion blur, akan direstorasi menggunakan matrik motion blur. Akan dianalisis bagaimana pengaruh matrik motion blur yang digunakan untuk memperbaiki citra dari segi pergeseran pixel dan sudut pergeseran.
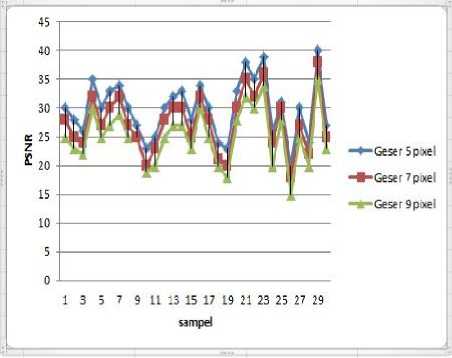
Gambar 8. Grafik perbandingan PSNR citra hasil pengurangan blur dengan sudut 0 derajat dengan pergeseran pixel berbeda
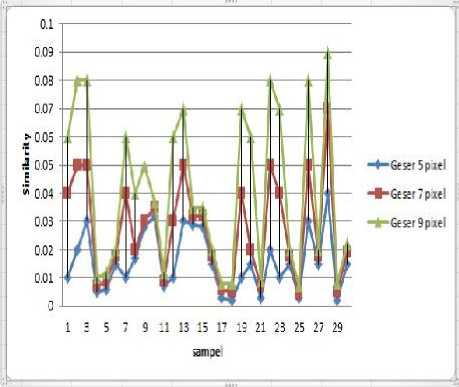
Gambar 9. Grafik perbandingan similarity citra hasil pengurangan blur dengan sudut 0 derajat dengan pergeseran pixel berbeda
Dari gambar 8 dan 9 dapat dilihat untuk setiap sampel terjadi penurunan PSNR dan peningkatan nilai Similarity untuk setiap pertambahan jumlah pergeseran pixel, jadi dapat disimpulkan semakin besar jumlah pergeseran pixel maka semakin kecil PSNR dan semakin besar nilai Similarity yang dihasilkan. Ini berarti bahwa semakin kuat citra
terdegradasi blur maka hasil proses pengurangan blur dengan Steepest Descent menghasilkan PSNR hasil yang semakin kecil dan Similarity hasil semakin besar.
Tabel 1. Perbandingan PSNR dan Similarity Citra Blur
Geser 7 pixel sudut 10 diperbaiki dengan matrik geser 7 pixel dengan sudut berbeda
|
Geser 7 pixel sudut 10 derajat |
Geser 7 pixel sudut 0 derajat |
Geser 7 pixel sudut 5derajat | ||||
|
S a m p e l |
PSN R Blur |
Simi larity Blur |
PSNR De blur |
Simi larity Deblur |
PSNR De Blur |
Simi larity Deblur |
|
1 |
24.78 |
0.041 |
26.38 |
0.0289 |
25.04 |
0.0390 |
|
2 |
26.67 |
0.009 |
27.59 |
0.0075 |
25.60 |
0.0119 |
|
3 |
26.98 |
0.046 |
28.98 |
0.0290 |
28.04 |
0.0360 |
|
4 |
17.77 |
0.119 |
18.93 |
0.0923 |
17.05 |
0.1440 |
|
5 |
40.03 |
0.001 |
41.50 |
0.0004 |
40.63 |
0.0005 |
Tabel 2. Perbandingan PSNR dan Similarity Citra Blur Geser 7 pixel sudut 10 diperbaiki dengan matrik geser 7 pixel dengan sudut 25 derajat
|
Geser 7 pixel sudut 10 derajat |
Geser 7 pixel sudut 25 derajat | |||
|
S a m p e l |
PSN R Blur |
Similar ity Blur |
PSNR De blur |
Similarity DeBlur |
|
1 |
24.78 |
0.041 |
19.31 |
0.1491 |
|
2 |
26.67 |
0.009 |
18.30 |
0.0640 |
|
3 |
26.98 |
0.046 |
22.91 |
0.1171 |
|
4 |
17.77 |
0.119 |
10.71 |
0.6246 |
|
5 |
40.03 |
0.001 |
34.45 |
0.0022 |
Pada tabel 1 dan 2 dapat dilihat untuk sudut 0 dan 5 derajat terjadi peningkatan nilai PSNR dan penurunan nilai Similarity, namun pada saat sudut 25 derajat terjadi penurunan kualitas citra hasil pengurangan blur. Sehingga dapat disimpulkan sudut memiliki pengaruh terhadap kualitas citra hasil pengurangan blur, sudut yang cukup besar mengakibatkan penurunan kualitas citra.
-
4. KESIMPULAN
Dari pengujian performansi dan analisis yang telah dilakukan terhadap citra uji yang digunakan maka dapat disimpulkan :
-
1) Berdasarkan analisis terhadap nilai PSNR dan Similarity citra hasil pengurangan blur, secara umum dapat dikatakan bahwa Metode Steepest Descent dapat diterapkan untuk pengurangan blur pada citra digital namun kurang handal untuk intensitas blur yang tinggi.
-
2) Metode Steepest Descent menghasilkan kualitas citra yang lebih baik, pada matrik tebakan yang memiliki intensitas yang hampir sama atau lebih
kecil dengan intensitas blur pada saat pembangkitan blur.
-
3) Untuk motion blur kurang cocok diperbaiki dengan matrik tebakan motion blur yang mempunyai sudut pergeseran, karena mengakibatkan terjadi penurunan kualitas citra hasil pengurangan blur yang terjadi pada sudut tertentu.
-
5. DAFTAR PUSTAKA
-
[1] . A.Sid-Ahmed, Maher. 1994. “Image
Processing”. Mc Graw-Hill, Inc.
-
[2] . C. Gonsales, Rafael and E. Woods, Richard.2001.”Digital Image Processing Second Edition”. Person Education International.
Peramalan 1999
-
[3] . Jain, Anil K,”Fundamental of Digital Image Processing”, Prentice Hall International Editions, 1989
-
[4] . Alex Rav-Acha, Shmuel Peleg, “Two Motion Blurred Images are Better than One”. The Hebrew University of Jerussalem, December 2004
-
[5] . G. Nagy, James, Katrina Palmer and Lisa Perrone, “Iterative Methods for image Debluring : A Matlab Object Oriented Approach”, Mathematics and Computer Science, Emory University, October 2003
-
[6] . G. Nagy, James and Jonathan M. Bardsley,”Preconditioning Strategies for a NonnegativelyContrained Steepest Descent Algorithm”, Mathematics and Computer Science, Emory University
-
[7] . N.Andrei,”Hybrid Conjugate Gradient Algorithm for Unconstrained Optimization", J Optim Theory App 141:249-264(2009)
-
[8] . Andreas Asheim and Daan Huybrechs, “Asymptotic Analysis of Numerical Steepest Descent with Path Approximations “. Springer, Math.Comput 647-671 (2010)
-
[9] . Richard Shewchuck, Jonathan,”Introduction to the Conjugate Gradient Method without the Agonizing Pain”, School of Computer Science Carnegie Mellon University, 1994
-
[10] . Tamir Sagi, Arie Feur and Michael Elad, ”The Periodic Step Gradient Descent Algorithm General Analysis and Application to Super Resolution Recontruction Problem”, Israel Institute of Technology.
-
[11] . Victor Solo, Xuan Kong “Adaptive Signal Processing Algorithms Stability and Performance”, Prentice Hall, New Jersey 1995
Teknologi Elektro
23
Vol. 12 No. 1 Januari - Juni 2013
Discussion and feedback