Aplikasi TSP Menggunakan Algoritma A star (Studi Kasus: Distributor Barang
on
JNATIA Volume 1, Nomor 1, November 2022
Jurnal Nasional Teknologi Informasi dan Aplikasinya
Penentuan Rute Terpendek Menggunakan Algoritma A Star
(Studi Kasus: Distributor Barang)
Rasita Natasya Br Sitepua1, I Gusti Ngurah Anom Cahyadi Putraa2
aProgram Studi Informatika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana
Badung, Bali, Indonesia
Abstrak
Penentuan rute terpendek adalah permasalahan yang sangat umum dikalangan masyarakat. Dimana kecepatan waktu, jarak dan biaya minimum sangat penting dalam pekerjaan maupun perjalanan seseorang. Distributor barang merupakan salah satu pekerjaan yang harus menempuh banyak lokasi dalam pengantaran barang. Namun, lokasi tujuan yang menyebar luas di berbagai wilayah menyulitkan para distributor untuk mendistributorkan barang dengan cepat. Penyebab lainnya karena banyaknya jalan raya terlebih lagi volume kendaraan yang banyak sering kali menyulitkan seseorang untuk mencari jalur terpendek ke tempat tujuan yang terdekat, baik dari segi jarak maupun waktu tempuh. Dari ranah bidang ilmu Informatika, permasalahan penentuan rute terpendek dapat diselesaikan menggunakan beberapa algoritma, salah satunya adalah algoritma A Star. Algoritma A Star adalah salah satu algoritma pencarian graf dengan menggunakan fungsi jarak-plus-biaya untuk menentukan urutan titik yang akan dikunjungi. Dalam permasalahan ini yang harus dipecahkan adalah bagaimana cara agar bisa mengunjungi tempat yang dituju dengan jarak, waktu dan biaya yang minimum. Pada penelitian ini menggunakan data primer berupa 17 titik toko yang sudah ditentukan di wilayah kota Denpasar berupa lokasi sebagai simpul dan jarak antar toko. Pada penelitian ini, penentuan rute terpendek menggunakan algoritma A Star dapat menerima input graf, program dapat menghitung lintasan terpendek, program dapat menampilkan lintasan terpendek serta jaraknya, program dapat menerima input peta dengan Google Map API dan menampilkan peta dan program menampilkan waktu proses program dalam menentukan rute terpendek.
Keywords: A Star, Rute Terpendek, Graf
Distributor merupakan suatu kelompok usaha yang melakukan distribusi penyaluran produk ke suatu tempat ke tempat lain. Peranan distributor sangat penting dalam menjamin ketersediaan dan pemasaran produk yang dibutuhkan oleh masyarakat. Distributor sebagai jalur perantara pemasaran baik transportasi maupun penyimpanan suatu produk barang dan jasa dari produsen ke konsumen. Dalam melakukan pemasaran tentunya distributor melakukan perjalanan pengantaran barang ke banyak tempat. Saluran distribusi sangat dipengaruhi faktor jalur pengiriman barang yang efisien sehingga bisa menghemat waktu dan biaya.
Namun tidak jarang distributor mengalami kendala saat melakukan pengantaran barang, seperti waktu perjalanan yang terlalu lama dan bingung memilih tujuan mana yang terlebih dahulu dikunjungi. Salah satu penyebabnya karena luasnya wilayah yang harus ditempuh. Seperti dikutip pada artikel simplidots, Jowan Kho “Wilayah yang luas menyebabkan tingkat kesulitan yang tinggi dalam hal pendistribusian barang karena memakan lebih banyak biaya transportasi dan Sumber Daya Manusia (SDM)”. Penyebab lainnya disebabkan karena banyaknya jalan raya, terlebih lagi volume kendaraan yang banyak sering kali menyulitkan seseorang untuk mencari jalur terpendek ke tempat tujuan yang terdekat, baik dari segi jarak maupun waktu tempuh.
Algoritma A Star adalah sebuah algoritma yang telah diperkaya dengan menerapkan suatu heuristik. Algoritma ini membuang langkah-langkah yang tidak perlu dengan pertimbangan bahwa langkah-langkah yang dibuang sudah pasti merupakan langkah yang tidak akan mencapai solusi yang diinginkan [8]. Algoritma A*(star) melakukan pencarian rute terdekat dengan melakukan perhitungan heuristik. Dari heuristik yang diperoleh, kemudian mencari nilai f(n). Nilai f(n) yang diperoleh akan dimasukkan kedalam open list. Tahap selanjutnya adalah mempertimbangkan bobot antar simpul dimana simpul dengan bobot terkecil yang akan dilalui. Simpul dengan bobot terkecil akan dimasukkan kedalam closed list dimana simpul dalam closed list akan dipilih sebagai simpul yang akan dilalui [10]. Algoritma A Star menghitung semua kemungkinan dan menyimpannya sehingga jika setiap memilih jalan. Algoritma A Star juga membandingkan dengan jalan lain yang disimpan. Sehingga hasil pencarian sikel terpendek dengan menggunakan algoritma ini akan menghasilkan hasil yang lebih optimum [2].
Penelitian [4] menggunakan algoritma A Star karena memiliki kemampuan optimasi yang optimal dan komplit untuk menyelesaikan permasalahan pencarian rute terpendek. Optimal berarti rute yang dihasilkan adalah rute yang paling baik dan komplit berarti algoritma tersebut dapat mencapai tujuan yang diharapkan.
Berdasarkan penelitian yang dilakukan sebelumnya, pada penelitian ini penulis melakukan penentuan rute terpendek perjalanan distributor sebuah perusahaan menggunakan algoritma A Star. Pencarian rute terpendek diawali dengan mengetahui posisi asal dan tujuan perjalanan distributor. Posisi asal dan tujuan perjalanan distributor yang telah diketahui akan digunakan pada proses pencarian rute terpendek.
Data yang akan digunakan pada penelitian ini adalah data primer. Data berupa 17 titik toko yang sudah ditentukan di wilayah kota Denpasar berupa lokasi sebagai vertex dan jarak antar toko. Jarak yang diperoleh akan menjadi inputan pada sistem dengan jumlah vertex yang berbeda sesuai dengan tujuan pengiriman. Hasil rute dinilai berdasarkan jarak dengan mengabaikan indeks kemacetan dan kondisi geografis rute. Penentuan setiap lokasi ditentukan dengan menggunakan Google Earth sebagai titik tujuan dan Google Maps API untuk menentukan jarak antar titik dengan metode observasi mandiri.
Graf digunakan untuk mempresentasikan suatu objek diskrit dan hubungan antar objek-objek tersebut. Secara visual, suatu objek di graf direpresentasikan dengan sebuah titik, dan suatu hubungan antar objek direpresentasikan dengan sebuah garis yang menghubungkan kedua titik. Graf bisa digunakan untuk mepresentasikan berbagai hal, salah satu kegunaan graf adalah untuk mempresentasikan sebuah peta[11].
Algoritma A Star adalah algoritma pencarian rute terpendek yang merupakan algoritma yang dituntun oleh fungsi heuristiknya, yang menentukan urutan simpul mana yang akan dikunjungi terlebih dahulu. Heuristik merupakan penilai yang memberi harga pada tiap simpul yang memandu A Star mendapatkan solusi yang diinginkan [2]. Untuk mencari jarak terdekat pada sebuah peta, peta harus direpresentasikan dengan sebuah graf. Simpul-simpul di graf tersebut merupakan representasi persimpangan-persimpangan di wilayah peta tersebut dan sisinya merupakan representasi jalan yang dapat dilalui. Sisi-sisi graf ini harus merupakan sisi berbobot yang nilainya mempresentasikan panjang lintasan. A Star mengevaluasi node dengan menggabungkan g(n), yaitu cost untuk mencapai node, dan h(n), yaitu cost yang diperlukan dari node untuk mencapai tujuan, dalam notasi matematika dituliskan sebagai [6]:
f(n) = g(n) + h(n)
Keterangan:
-
1. f(n) adalah jumlah dari g(n) dan h(n). ini adalah perkiraan jalur terpendek sementara. maka f(n) adalah jalur terpendek yang sebenarnya yang tidak ditelusuri sampai Algoritma A-Star (A*) diselesaikan.
-
2. g(n)/Geographical Cost adalah total jarak yang didapat dari verteks awal ke verteks sekarang (halangan).
-
3. h(n)/Heuristic Cost adalah perkiraan jarak dari vertex sekarang (yang sedang dikunjungi) ke vertek tujuan. sebuah fungsi heuristic digunakan untuk membuat perkiraan seberapa jauh lintasan yang akan diambil ke vertex tujuan.
Beberapa istilah yang terdapat pada algoritma A Star [5]:
-
1. Starting point merupakan terminologi untuk posisi awal .
-
2. Simpul (node) merupakan titik yang merepresentasikan suatu tujuan. Bentuknya dapat berupa persegi, segitiga, ataupun lingkaran
-
3. A merupakan simpul yang sedang berjalan dalam pencarian jalur terpendek
-
4. Open list merupakan simpul yang mungkin diakses dari starting point maupun simbol yang sedang dijalankan.
-
5. Closed List merupakan simpul yang telah dipilih sebagai pemilihan dari jalur terpendek.
-
6. Harga (F) adalah nilai yang diperoleh dari penjumlahan nilai G, jumlah nilai tiap simpul
dalam jalur terpendek dari starting point ke A, dan H, jumlah nilai perkiraan dari sebuah simpul ke simpul tujuan.
Prinsip algoritma ini adalah mencari jalur terpendek dari sebuah simpul awal (starting point) menuju simpul tujuan dengan memperhatikan harga (F) terkecil.
Gambar 1 menunjukkan flowchart dari algoritma A Star dalam menentukan rute terpendek.
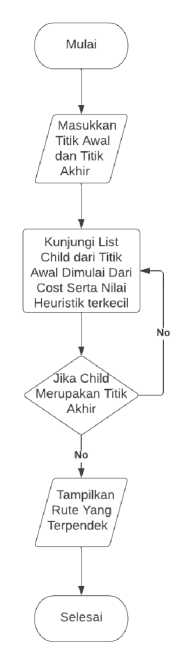
Gambar 1 Flowchart Algoritma A Star
Gambar 1 1
Langkah-langkah algoritma A Star, sebagai berikut [5]:
-
1. Mulai.
-
2. Node A sebagai starting point
-
3. Memasukkan seluruh simpul yang bertetangga dan tidak memilik atribut rintangan dengan A ke dalam open list.
-
4. Kemudian mencari nilai H terkecil dari simpul-simpul dalam open list tersebut.
-
5. Kemudian memindahkan A ke simpul yang memiliki nilai H terkecil. Simpul sebelum A
disimpan sebagai parent dari A dan dimasukkan ke dalam closed list. Jika terdapat simpul lain yang bertetangga dengan A (yang sudah berpindah) namun belum termasuk kedalam anggota open list, maka masukkan simpul-simpul tersebut ke dalam open list.
-
6. Setelah itu, bandingkan nilai G yang ada dengan nilai G sebelumnya (pada langkah awal, tidak perlu dilakukan perbandingan nilai G). Jika nilai G sebelumnya lebih kecil maka A kembali keposisi awal. Simpul yang pernah dicoba dimasukkan ke dalam closed list. Hal terebut dilakukan berulang-ulang hingga terdapat solusi atau tidaka ada lagi simpul lain yang berada pada open list.
Pada penelitian ini, data lokasi akan ditelusuri berdasarkan latitude dan longitude dari peta. Proses algoritma A Star dalam menentukan rute terpendek perjalanan distributor sebuah perusahaan diimplementasikan pada bahasa pemrograman Python. Tabel 1 berikut ini adalah titik tujuan pengiriman barang yang akan digunakan.
Tabel 1. Latitude dan Longitude Titik Tujuan
|
No |
Titik Tujuan |
Latitude |
Longitude |
|
1 |
Alfamart Jl. Gunung Agung |
-8.6513942 |
1115.1960404 |
|
2 |
Alfamart Nusa Kambangan |
-8.6643461 |
115.2124206 |
|
3 |
Alfamart Jl. Surapati |
-8.65641 |
115.22092 |
|
4 |
Alfamart Jl. Hayam Wuruk |
-8.65718 |
115.23872 |
|
5 |
Alfamart Pemecutan Kaja |
-8.6391827 |
115.2090748 |
|
6 |
Alfamart Jl. WR Supratman |
-8.6337537 |
115.256471 |
|
7 |
Alfamart Ubung Kaja |
-8.6156725 |
115.1941227 |
|
8 |
Indomaret Tukad Pakerisan |
-8.6887938 |
115.2261427 |
|
9 |
Indomaret Pulau Kawe |
-8.6777391 |
115.2064918 |
|
10 |
Indomaret Buana Raya |
-8.6610016 |
115.1876713 |
|
11 |
Indomaret Merdeka |
-8.6647901 |
115.2403174 |
|
12 |
Indomaret Hayam Wuruk |
-8.6572924 |
115.2278695 |
|
13 |
Indomaret Gatsu Timur |
-8.6357861 |
115.2264692 |
|
14 |
Indomaret Seroja |
-8.6342537 |
115.2296348 |
|
15 |
Indomaret Green Kori |
-8.6108441 |
115.1992835 |
|
16 |
Indomaret Trenggana |
-8.6181574 |
115.2407235 |
|
17 |
indomaret pulau galang |
-8.6955229 |
115.1903073 |
Berdasarkan latitude dan longitude dihitung jarak untuk setiap titik tujuan pengiriman barang menggunakan persamaan (?) berikut ini:
dij = (69 ∙ √(loni - Iortj)2 + (lati - Iatj)2') ∙ 1,60934 Dimana:
-
• dij = jarak antara 2 titik koordinat i dan j (dalam km)
-
• loni = titik longitude i
-
• lonj = titik longitude j
-
• lati = titik latitude i
-
• latj = titik latitude j
Proses jarak masing-masing titik
def haversineDist(n1, n2):
-
# Menghitung jarak dari node n1 dan n2 berdasarkan longitude dan latitude
-
# Menggunakan Haversine formula dalam meter
-
# Aproksimasi radius bumi dalam km
R = 6373.0
lat1 = radians(n1.x)
lon1 = radians(n1.y)
lat2 = radians(n2.x)
lon2 = radians(n2.y)
dlon = lon2 - lon1
dlat = lat2 - lat1
a = sin(dlat / 2)**2 + cos(lat1) * cos(lat2) * sin(dlon /2)**2
c = 2 * atan2(sqrt(a), sqrt(1 -a))
distance = R * c
Berdasarkan perhitungan jarak masing-masing tujuan distributor dengan persamaan di atas, diperoleh hasil jarak pada tabel 2 di bawah ini.
Tabel 2. Jarak Masing-Masing Titik Tujuan
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 | |
|
1 |
0.0 0 |
5.8 2 |
7.1 1 |
9.0 7 |
1.9 7 |
7.2 6 |
5.0 6 |
6.6 8 |
4.1 9 |
1.4 1 |
9.4 1 |
7.8 8 |
3.9 2 |
4.3 1 |
5.3 1 |
6.4 8 |
6.8 5 |
|
2 |
5.8 2 |
0.0 0 |
1.2 9 |
3.2 5 |
7.7 9 |
6.5 1 |
10. 88 |
4.1 1 |
1.6 3 |
4.4 1 |
3.6 6 |
2.0 6 |
9.7 4 |
9.4 6 |
11. 13 |
8.9 6 |
4.2 9 |
|
3 |
7.1 1 |
1.2 9 |
0.0 0 |
1.9 6 |
9.0 8 |
5.2 2 |
12. 17 |
5.4 0 |
2.9 1 |
5.7 0 |
2.3 7 |
0.7 7 |
8.5 6 |
8.1 7 |
12. 41 |
7.6 7 |
5.5 7 |
|
4 |
9.0 7 |
3.2 5 |
1.9 6 |
0.0 0 |
8.5 4 |
3.2 6 |
11. 63 |
3.9 6 |
4.8 8 |
7.6 6 |
0.8 6 |
1.1 9 |
6.6 0 |
6.2 1 |
11. 88 |
5.7 1 |
7.5 4 |
|
5 |
1.9 7 |
7.7 9 |
9.0 8 |
8.5 4 |
0.0 0 |
5.2 9 |
3.0 9 |
8.6 5 |
6.1 7 |
3.3 8 |
9.4 1 |
9.7 4 |
1.9 5 |
2.3 4 |
3.3 3 |
4.5 0 |
8.8 3 |
|
6 |
7.2 6 |
6.5 1 |
5.2 2 |
3.2 6 |
5.2 9 |
0.0 0 |
8.3 8 |
7.2 1 |
8.1 3 |
8.6 7 |
4.1 2 |
4.4 5 |
3.3 4 |
2.9 5 |
8.6 2 |
2.4 5 |
10. 79 |
|
7 |
5.0 6 |
10. 88 |
12. 17 |
11. 63 |
3.0 9 |
8.3 8 |
0.0 0 |
11. 74 |
9.2 6 |
6.4 7 |
12. 50 |
12. 83 |
5.0 4 |
0.3 9 |
0.7 8 |
7.5 9 |
11. 92 |
|
8 |
6.6 8 |
4.1 1 |
5.4 0 |
3.9 6 |
8.6 5 |
7.2 1 |
11. 74 |
0.0 0 |
2.4 9 |
5.2 7 |
3.0 9 |
4.6 9 |
10. 55 |
10. 16 |
11. 99 |
9.6 6 |
5.1 5 |
|
9 |
4.1 9 |
1.6 3 |
2.9 1 |
4.8 8 |
6.1 7 |
8.1 3 |
9.2 6 |
2.4 9 |
0.0 0 |
2.7 8 |
5.2 9 |
3.6 8 |
8.1 2 |
8.5 1 |
9.5 0 |
10. 58 |
2.6 6 |
|
1 0 |
1.4 1 |
4.4 1 |
5.7 0 |
7.6 6 |
3.3 8 |
8.6 7 |
6.4 7 |
5.2 7 |
2.7 8 |
0.0 0 |
8.0 7 |
6.4 7 |
5.3 3 |
5.7 2 |
6.7 2 |
7.8 9 |
5.4 4 |
|
1 1 |
9.4 1 |
3.6 6 |
2.3 7 |
0.8 6 |
9.4 1 |
4.1 2 |
12. 50 |
3.0 9 |
5.2 9 |
8.0 7 |
0.0 0 |
1.6 0 |
7.4 6 |
7.0 7 |
12. 74 |
6.5 7 |
7.9 5 |
|
1 2 |
7.8 8 |
2.0 6 |
0.7 7 |
1.1 9 |
9.7 4 |
4.4 5 |
12. 83 |
4.6 9 |
3.6 8 |
6.4 7 |
1.6 0 |
0.0 0 |
7.7 9 |
7.4 0 |
13. 07 |
6.9 0 |
6.3 4 |
|
1 3 |
3.9 2 |
9.7 4 |
8.5 6 |
6.6 0 |
1.9 5 |
3.3 4 |
5.0 4 |
10. 55 |
8.1 2 |
5.3 3 |
7.4 6 |
7.7 9 |
0.0 0 |
0.3 9 |
5.2 8 |
2.5 5 |
10. 78 |
|
1 |
4.3 |
9.4 |
8.1 |
6.2 |
2.3 |
2.9 |
0.3 |
10. |
8.5 |
5.7 |
7.0 |
7.4 |
0.3 |
0.0 |
5.6 |
2.1 |
11. |
|
4 |
1 |
6 |
7 |
1 |
4 |
5 |
9 |
16 |
1 |
2 |
7 |
0 |
9 |
0 |
7 |
7 |
17 |
|
1 |
5.3 |
11. |
12. |
11. |
3.3 |
8.6 |
0.7 |
11. |
9.5 |
6.7 |
12. |
13. |
5.2 |
5.6 |
0.0 |
7.8 |
12. |
|
5 |
1 |
13 |
41 |
88 |
3 |
2 |
8 |
99 |
0 |
2 |
74 |
07 |
8 |
7 |
0 |
3 |
16 |
|
1 |
6.4 |
8.9 |
7.6 |
5.7 |
4.5 |
2.4 |
7.5 |
9.6 |
10. |
7.8 |
6.5 |
6.9 |
2.5 |
2.1 |
7.8 |
0.0 |
13. |
|
6 |
8 |
6 |
7 |
1 |
0 |
5 |
9 |
6 |
58 |
9 |
7 |
0 |
5 |
7 |
3 |
0 |
24 |
|
1 |
6.8 |
4.2 |
5.5 |
7.5 |
8.8 |
10. |
11. |
5.1 |
2.6 |
5.4 |
7.9 |
6.3 |
10. |
11. |
12. |
13. |
0.0 |
|
7 |
5 |
9 |
7 |
4 |
3 |
79 |
92 |
5 |
6 |
4 |
5 |
4 |
78 |
17 |
16 |
24 |
0 |
Berdasarkan parameter yang digunakan serta jarak antar titik tujuan, maka diperoleh proses pencarian rute pada source code berikut ini:
Proses Pencarian Rute
-
# Buat graf dari nama graf input
g = makeGraphFromTxt(graphName, end)
-
# Cari node start dan end
startNode = g.findNode(start) endNode = g.findNode(end)
-
# Make priority queue to store nodes q = queue.PriorityQueue()
-
# Deklarasikan dictionary kosong untuk rekam jejak parent dan rekam jejak total
-
# jarak kumulatif yang paling singkat untuk ke node tertentu jalur = {}
kumulatifMeter = {}
-
# Inisiasi dengan none, karena parent dari starting node tidak ada, dan 0.0
-
# untuk jarak kumulatif, karena jarak dari start ke start adalah 0
jalur[start] = None
kumulatifMeter[start] = 0.0
-
# Set starting node
q.put((0, start))
-
# Inisiasikan currNodeName dengan nilai acak agar bisa masuk ke loop
currNodeName = -999
-
# jalankan loop asalkan belum sampai tujuan atau masih ada elemen prioqueue
while (q.qsize() > 0 and currNodeName != end):
(currPrio, currNodeName) = q.get()
for nextNodeName in g.findNode(currNodeName).neighbors:
addedMeter = kumulatifMeter[currNodeName] + g.findNode(
currNodeName).neighbors[nextNodeName]
-
# menambahkan kumulatifMeter baru apabila belum ada dictionary key : nextNodeName if (not (nextNodeName in kumulatifMeter)):
-
# menambahkan kumulatifMeter baru
kumulatifMeter[nextNodeName] = addedMeter
-
# prioritas untuk nextNodeName dikalkulasi dengan menambahkan addedMeter dan nilai
-
# heuristik nextNodeName
nextPrio = addedMeter + g.findNode(nextNodeName).heuristik
-
# memasukan prio dan nama node ke dalam prioqueue q.put((nextPrio, nextNodeName)) # menambahkan riwayat jalur
jalur[nextNodeName] = currNodeName
-
# menambahkan kumulatifMeter baru apabila kumulatifMeter yang sebelumnya
-
# ternyata tidak optimal
if (addedMeter < kumulatifMeter[nextNodeName]):
-
# menambahkan kumulatifMeter baru
kumulatifMeter[nextNodeName] = addedMeter
-
# prioritas untuk nextNodeName dikalkulasi dengan menambahkan
addedMeter dan nilai
-
# heuristik nextNodeName
nextPrio = addedMeter + g.findNode(nextNodeName).heuristik
-
# memasukan prio dan nama node ke dalam prioqueue
q.put((nextPrio, nextNodeName))
-
# menambahkan riwayat jalur
jalur[nextNodeName] = currNodeName
-
# skema pencetakan hasil
if (currNodeName == end):
-
# mencetak jarak terpendek antar node awal dan tujuan
print(
f"Jarak terpendek dari {start} ke {end}: {kumulatifMeter[end]} km \n")
print("Lintasan:")
-
# list untuk nanti dibalikan
reverseDirection = []
-
# iterasi mulai dari element parent ending node
iterPrint = jalur[end]
-
# selagi belum none (iterprint merupakan elemen parent dari starting node) while (iterPrint != None):
-
# append ke list kemudian iterasikan berikutnya
reverseDirection.append(iterPrint)
iterPrint = jalur[iterPrint]
-
# print array dengan orientasi reverse agar dari node awal-tujuan
for nodeName in reversed(reverseDirection):
print(nodeName, end=" → ")
-
# node tujuan
print(end, end="\n\n")
Sesuai dengan proses pencarian rute di atas, maka diperoleh rute terpendek perjalanan sebuah distributor sesuai titik awal dan titik tujuan yang diinginkan.
Output:
lMasukkan nama simpul awal: Indomaret Trenggana
■Masukkan nama simpul tujuan: Alfamart Ubung Kaja
,3arak terpendek dari Indomaret Trenggana ke Alfamart Ubung Kaja: 7.592599999999999 m
'Lintasan:
-Indomaret Trenggana → Indomaret Seroja → Indomaret Gatsu Timur → Alfamart Pemecutan Kaja → Alfamart Ubung Kaja
’Running Time : θ.00193 second
Proses pencarian rute dengan graf
def makeGraphFromTxt(file_name, end):
-
# Get current path
currpath = str(os.getcwd()).split('\\')
-
# Membuat graph dari file eksternal .txt
-
# Open dan read file berdasarkan current path if (currpath[len(currpath)-1] in ["src", "bin"]):
f = open(f"../test/{file_name}.txt","r")
else:
f = open(f"./test/{file_name}.txt", "r") # Iterate line file lines = f.readlines()
size = int(lines[0]) graph = Graph(size)
-
# Add adjacency matrix ke graph
for i in range(size + 1, len(lines)):
line = lines[i].split(" ") for i in range(len(line)):
line[i] = int(line[i].replace("\n", "")) graph.addAdjm(line)
-
# Add node ke graph
for i in range(1, size + 1): line = lines[i].split(",") for i in range(len(line)):
line[i] = line[i].replace("\n", "")
curr_node = Node(line[0], float(line[1]), float(line[2])) graph.addNode(curr_node)
-
# Cari node akhir
for node in graph.nodes:
if (node.name == end):
endNode = node
-
# Add nilai heuristik masing-masing node
for node in graph.nodes:
node.calcHeuristik(endNode)
-
# Add edge ke graph
for i in range(len(graph.adjm)):
for j in range(len(graph.adjm)):
if (graph.adjm[i][j] == 1):
(graph.nodes[i]).addNeighbors( graph.nodes[j], haversineDist(graph.nodes[i], graph.nodes[j])) return graph
Output:
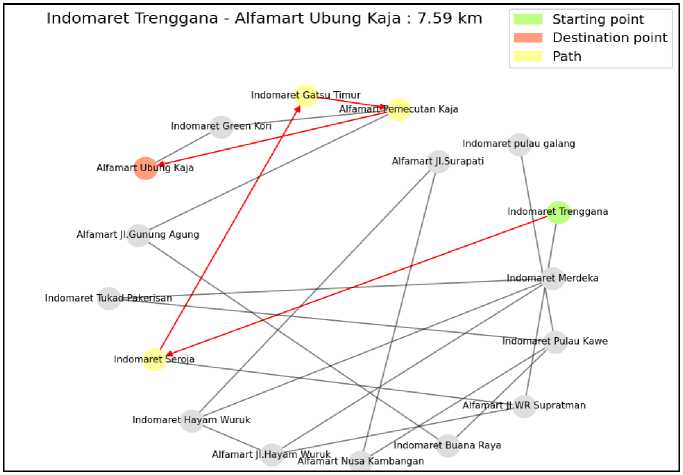
Gambar 2 Graf yang dihasilkan
Proses pengujian dilakukan dengan melakukan perubahan pada titik awal dan titik tujuan. Hasil dari pengujian dengan algoritma A Star terlihat pada tabel 4 di bawah ini:
Tabel 4. Hasil Pengujian Sistem
|
N o |
Titik Awal |
Titik Tujuan |
Rute |
Jarak Terbaik (km) |
Waktu (s) |
|
1 |
indomaret Trenggana |
Alfamart Ubung Kaja |
Indomaret Trenggana → Indomaret Seroja → Indomaret Gatsu Timur → Alfamart Pemecutan Kaja → Alfamart Ubung Kaja |
7.59 |
0.00193 |
|
2 |
Alfamart Jl.Surapati |
Indomaret Merdeka |
Alfamart Jl.Surapati → Indomaret Hayam Wuruk → Indomaret Merdeka |
2.37 |
0.00255 |
|
3 |
Indomaret Seroja |
Alfamart Nusa Kambangan |
Indomaret Seroja → Alfamart Jl.WR Supratman → Alfamart Jl.Hayam Wuruk → Indomaret Hayam Wuruk → Alfamart Jl.Surapati → Alfamart Nusa Kambangan |
9.45 |
0.00274 |
|
4 |
Indomaret Hayam Wuruk |
Alfamart Pemecutan Kaja |
Indomaret Hayam Wuruk → Alfamart Jl.Hayam Wuruk → Alfamart Jl.WR Supratman → Indomaret Seroja → Indomaret Gatsu Timur → Alfamart Pemecutan Kaja |
9.73 |
0.00218 |
|
5 |
Indomaret Tukad Pakerisan |
Indomaret Green Kori |
Indomaret Tukad Pakerisan → Indomaret Pulau Kawe → Indomaret Buana Raya → Alfamart Jl.Gunung Agung → Alfamart Pemecutan Kaja → Indomaret Green Kori |
11,98 |
0.00233 |
|
6 |
Alfamart Jl.Gunung Agung |
Indomaret Trenggana |
Alfamart Jl.Gunung Agung → Alfamart Pemecutan Kaja → Indomaret Gatsu Timur → |
6.47 |
0.00213 |
|
Indomaret Seroja → Indomaret Trenggana | |||||
|
7 |
Alfamart Jl.Hayam Wuruk |
Indomaret pulau galang |
Alfamart Jl.Hayam Wuruk → Indomaret Hayam Wuruk → Alfamart Jl.Surapati → Alfamart Nusa Kambangan → Indomaret Pulau Kawe → Indomaret pulau galang |
7.53 |
0.0028 |
|
8 |
Indomaret Pulau Kawe |
Indomaret Gatsu Timur |
Indomaret Pulau Kawe → Indomaret Buana Raya → Alfamart Jl.Gunung Agung → Alfamart Pemecutan Kaja → Indomaret Gatsu Timur |
8.11 |
0.002 |
Berdasarkan pengujian tersebut, menunjukkan bahwa program dapat menerima input graf, program dapat menghitung lintasan terpendek, program dapat menampilkan lintasan terpendek serta jaraknya, program dapat menerima input peta dengan Google Map API dan menampilkan peta dan program menampilkan waktu proses program dalam menentukan rute terpendek.
Pada penelitian ini, sistem penentuan rute terpendek perjalanan distributor sebuah perusahaan menggunakan algoritma A star telah berhasil dibangun dan diuji coba. Hasil dari sistem ini menunjukkan bahwa pencarian rute terpendek pada sebuah peta menggunakan algoritma A Star harus direpresentasikan dengan sebuah graf. Simpul-simpul graf tersebut representasi titik-titik lokasi pada peta tersebut dan sisinya merupakan representasi lintasan antar titik lokasi. Setiap sisi graf memiliki bobot atau jarak sehingga dapat dihitung nilai heuristiknya. Setelah informasi jarak dan nilai heuristic diketahui, pencarian menggunakan algoritma A star dapat dilakukan menggunakan pohon pencarian dan antrian prioritas. Pada penelitian ini, penentuan rute terpendek menggunakan algoritma A Star dapat menerima input graf, program dapat menghitung lintasan terpendek, program dapat menampilkan lintasan terpendek serta jaraknya, program dapat menerima input peta dengan Google Map API dan menampilkan peta dan program menampilkan waktu proses program dalam menentukan rute terpendek. Jika simpul awal indomaret Trenggana dan simpul tujuan Alfamart Ubung Kaja maka jarak terpendek yang didapatkan adalah 7.59 km dengan Lintasan Indomaret Trenggana → Indomaret Seroja → Indomaret Gatsu Timur → Alfamart Pemecutan Kaja → Alfamart Ubung Kaja dalam waktu program 0.00193 s.
Referensi
-
[1] Akhyar, M. (2017). PERBANDINGAN ALGORITMA GREEDY DAN TRAVELLING SALESMAN PROBLEM. Semarang: UNIVERSITAS NEGERI SEMARANG.
-
[2] Gede Wahyu Antara Dalem, I. B. (2018). Penerapan Algoritma A* (Star) Menggunakan Graph Untuk Menghitung Jarak Terpendek. Jurnal RESISTOR (Rekayasa Sistem Komputer), 1(1), 41–47. https://doi.org/10.31598/jurnalresistor.v1i1.253
-
[3] Hamidi, I., & Aldillah, D. (n.d.). Algoritma A * ( A Star ) Sebagai Salah Satu Contoh Metode Pemrograman Branch and Bound. 1–2.
-
[4] HARTANTO, K. (2020). ANALISIS PERBANDINGAN ALGORITMA DIJKSTRA DAN A STAR. Medan: UNIVERSITAS SUMATERA UTARA.
-
[5] Manurung, R. A. (2016). Perbandingan Algoritma a* Dan Breadth First.
-
[6] Putra, A. B. W., Rachman, A. A., Santoso, A., & Mulyanto, M. (2020). Perbandingan Hasil Rute Terdekat Antar Rumah Sakit di Samarinda Menggunakan Algoritma A*(star) dan Floyd-Warshall. Jurnal Sisfokom (Sistem Informasi Dan Komputer), 9(1), 59–68.
https://doi.org/10.32736/sisfokom.v9i1.685
-
[7] Putra, E. S. (2017). Pencarian Lintasan Terpendek Pada Aplikasi Navigasi Menggunakan Algoritma A *.
440
Discussion and feedback