Image Restoration Menggunakan Metode Lucy-Richardson pada Citra Digital
on
JNATIA Volume 2, Nomor 2, Februari 2024 p-ISSN: 2986-3929
Jurnal Nasional Teknologi Informasi dan Aplikasinya
Image Restoration Menggunakan Metode Lucy Richardson pada Citra Digital
Sammaditthi Gotamaa1, I Wayan Santiyasaa2,
aProgram Studi Informatika, Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Udayana, Bali
Jln. Raya Kampus UNUD, Bukit Jimbaran, Kuta Selatan, Badung, 08261, Bali, Indonesia 1sammaditthigotama@yahool.com
2 santiyasa@unud.ac.id (Corresponding Author)
Abstract
This journal discusses the use of the Lucy-Richardson method for image restoration on digital images. Digital images are often affected by noise or blur, which can cause the image to be too contrasted, out of focus, less sharp, and so on. Therefore, digital image processing technology is very important to improve image quality. Image restoration is one of the digital image processing techniques used to improve images that are affected by noise or blur. The Lucy-Richardson method is one of the methods that can be used to perform image restoration on digital images. In this journal, we will discuss the basic theory of the Lucy-Richardson method, the implementation of the Lucy-Richardson method on digital images, and the evaluation of the results of using the Lucy-Richardson method on digital images. The purpose of this journal is to provide a better understanding of the use of the Lucy-Richardson method for image restoration on digital images.
Keywords: Image restoration, Lucy-Richardson method, Digital Imaga, Noise
Restorasi Citra adalah suatu operasi pengondisian supaya gambar yang akan digunakan benar-benar memberikan informasi yang akurat secara geometris dan radiometris. Ini dilakukan untuk merekonstruksi atau mengembalikan gambar yang telah terdegradasi dengan menggunakan pemahaman tentang fenomena degradasi. Seperti yang diketahui, alat optik digital seperti kamera terkadang memiliki keterbatasan dalam menangkap gambar, yang menyebabkan gambar yang dihasilkan kabur atau suara, yang dalam dunia pemrosesan sinyal disebut sebagai suara. Keterbatasan ini dapat disebabkan oleh perangkat atau manusia. Oleh karena itu, restorasi citra sangat penting.[1].
Restoration Image bertujuan untuk menghilangkan atau mengurangi kerusakan gambar. Tujuannya hampir sama dengan operasi perbaikan gambar, tetapi penyebab kerusakan gambar sudah diketahui. Metode Lucy-Richardson untuk restorasi gambar digunakan untuk memperbaiki gambar tersebut, dan metode ini dapat menyelesaikan masalah di atas.
Pengolahan citra digital adalah proses pengolahan gambar atau citra yang dilakukan secara digital. Citra digital tersusun dari titik-titik yang disebut dengan piksel. Dalam citra digital, kita juga mengenal istilah resolusi citra yang berarti jumlah piksel yang terdapat pada citra. Pengolahan citra digital sangat penting dalam berbagai bidang, seperti bidang medis, fotografi, dan industri. Salah satu masalah yang sering dihadapi dalam pengolahan citra digital adalah adanya noise atau derau pada citra. Noise dapat menyebabkan citra menjadi terlalu kontras, objek gambar tidak fokus, kurang tajam, dan lain sebagainya. Oleh karena itu, teknik image restoration sangat penting untuk memperbaiki citra yang terkena noise atau blur.[3]
Metode Lucy-Richardson telah banyak digunakan dalam berbagai aplikasi, termasuk dalam bidang medis, fotografi, dan industri. Metode ini didasarkan pada konsep dekonvolusi, yaitu proses memperbaiki gambar yang terkena blur atau noise dengan menghilangkan efek blur.
atau noise tersebut. Metode ini juga f Fll-I1SF dapat digunakan untuk melakukan restorasi
gambar pada gambar digital.
Dalam jurnal ini, kami akan membahas penggunaan metode Lucy-Richardson pada citra digital untuk melakukan image restoration. Kami akan membahas teori dasar dari metode Lucy-Richardson, implementasi metode Lucy-Richardson pada citra digital, dan evaluasi hasil dari penggunaan metode Lucy-Richardson pada citra digital. Tujuan dari jurnal ini adalah untuk memberikan pemahaman yang lebih baik tentang penggunaan metode Lucy-Richardson untuk image restoration pada citra digital, sehingga dapat membantu dalam pengolahan citra digital yang lebih baik dan akurat.
Metodologi penelitian yang digunakan dalam jurnal ini adalah sebagai berikut:
Pengolahan citra digital (Digital Image Processing) merupakan disiplin ilmu yang mengkaji teknik pengolahan citra. Gambar yang dimaksud disini adalah gambar diam (photo) atau gambar bergerak (dihasilkan dari webcam). Sedangkan digital disini menunjukkan bahwa pengolahan gambar dilakukan secara digital dengan menggunakan komputer. Secara matematis, gambar adalah fungsi kontinu dengan intensitas cahaya dalam bidang dua dimensi. Agar dapat diproses oleh komputer digital, sebuah citra harus diberikan secara numerik dengan bilangan diskrit. Representasi fungsi kontinu menjadi nilai diskrit disebut digitasi gambar. Citra digital dapat direpresentasikan sebagai matriks dua dimensi f(x,y) yang terdiri dari M kolom dan N baris, di mana perpotongan antara kolom dan baris disebut pikse[1]l.
Restorasi citra merupakan langkah untuk mendapatkan citra yang lebih jelas dari citra yang rusak dengan hanya mengetahui beberapa elemen degradasi dari citra tersebut. pemulihan gambar berbeda dengan peningkatan gambar, tetapi keduanya berusaha untuk meningkatkan kualitas gambar. Peningkatan citra lebih berkaitan dengan ketajaman aspek-aspek tertentu pada citra, sedangkan restorasi citra memanfaatkan pengetahuan tentang proses degradasi untuk memulihkan citra aslinya[2]
Metode Lucy-Richardson (L-R), umumnya dikenal sebagai dekonvolusi Lucy-Richardson, ditemukan secara terpisah oleh Richardson (1972) dan Lucy (1974). Pendekatan ini efektif jika kita mengetahui PSF tetapi tidak tahu apa-apa tentang noise tambahan pada gambar. Pendekatan ini awalnya digunakan untuk memperbaiki foto astronomi, sebelum akhirnya digunakan secara luas untuk mengembalikan gambar yang buram. Pendekatan ini memaksimalkan kemungkinan (kemungkinan tertinggi) bahwa sebuah gambar ketika dipelintir dengan hasil PSF adalah sebuah contoh dari gambar yang buram, asalkan noise tersebar dengan distribusi Poison.
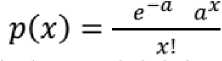
(1)
Dengan x adalah peubah acak dan a adalah konstanta. Esensi dari iterasi adalah sebagaiberikut: estimasi ke-(n +1) dari citra restorasi adalah estimasi ke-n citra restorasi dikali dengan citra koreksi. Persamaan iterasinya adalah:
(2)
/n+1 = /n (----^---) . reflect (PSF)
yang dalam hal ini, operator ∗ menyatakan konvolusi, f ̂ = f ̂ (x,y) menyatakan estimasi citra restorasi, g = g(x, y) menyatakan citra masukan (yang mengalami degradasi), reflect(PSF) menyatakan pencerminan PSF, yaitu Reflect ((PSF(x, y)) = PSF (–x, –y), dan(x, y)) = PSF (–x, – y), dan ( ⅛.FSF ) ∗ reflect (PSF) menyatakan citra koreksi. Dengan menggunakan metodologi penelitian ini, diharapkan dapat memberikan hasil yang akurat dan dapat dipertanggungjawabkan tentang penggunaan metode Lucy-Richardson untuk image restoration pada citra digital.
Sebagai jenis informasi visual, citra (gambar) adalah komponen multimedia yang sangat penting. Gambar yang penuh dengan informasi memiliki fitur yang tidak dimiliki oleh data teks. Sebuah gambar dapat memberikan lebih banyak informasi daripada seribu kata, menurut sebuah peribahasa, "Sebuah gambar bermakna lebih dari seribu kata." Namun, informasi yang ada di gambar seringkali berbeda dari yang ada di gambar. Dalam situasi seperti ini, gambar mengalami penurunan kualitas, seperti mengandung cacat atau derau, warna yang terlalu kontras, tajam atau kabur, dan sebagainya. Gambar yang rusak harus diubah menjadi gambar baru dengan kualitas yang lebih baik untuk membuatnya lebih mudah dipahami. Ini dilakukan melalui proses yang dikenal sebagai pengolahan gambar.
Perbaikan kualitas gambar digunakan dalam pengolahan gambar untuk meningkatkan cara penglihatan manusia memahami dan memahami gambar. Dikarenakan gambar menjadi sulit diinterpretasikan dan mengandung lebih sedikit informasi, gambar yang memiliki warna yang tidak tajam, kabur (blurring), atau noise (seperti bintik-bintik putih) akan dikurangi.
Apabila gambar yang mengandung suara langsung diproses dan diekstrak, fitur pentingnya dapat mengganggu akurasi. Oleh karena itu, lebih baik jika gambar dibersihkan dari suara sebelum diproses untuk mengekstrak fitur pentingnya.
Teknik Image Enhancement diperlukan untuk mempermudah memperbaiki kualitas gambar. Peningkatan gambar secara keseluruhan berarti meningkatkan atau meningkatkan kualitas gambar dengan algoritma tertentu. Proses image Enhancement terdiri dari sekumpulan teknik yang digunakan untuk meningkatkan tampilan visual sebuah gambar atau untuk mengubah gambar menjadi bentuk yang lebih sesuai untuk analisis mata manusia atau analisis mesin. Aplikasi yang dirancang akan menggunakan algoritma Lucy-Richardson, salah satu algoritma image enhancement yang paling dikenal.
Pertama, hal yang harus dilakukan untuk meningkatkan kualitas gambar adalah memasukkan gambar. Saya akan memasukkan gambar grayscale dalam format jpg, dan kami akan mencoba menghitung resolusi gambar 5 x 5. Gambar grayscale yang dimasukkan dapat dilihat di bawah ini.
|
r221 |
216 |
199 |
179 |
171 |
|
181 |
180 |
172 |
159 |
156 |
|
139 |
144 |
142 |
135 |
135 |
|
120 |
129 |
131 |
124 |
121 |
|
∣-255 |
255 |
255 |
250 |
242-∣ |
Selanjutnya nilai tersebut akan kita kalikan dengan kernel (PSF)
0.1096 0.1118 0.1096
0.1118 0.1141 0.1118
0.1096 0.1118 0.1096
Kernel diatas merupakan nilai yang didapat dari PSF blur gaussian, dengan menggunakan tools matlab R2103a. Dengan perintah coding PSF=fspecial(‘gaussian’,3,5);.Setelah memperolehnilai blur, langkah berikutnya adalah memperbaiki kembali nilai blur menggunakan algoritma Lucy-Richardson. Dalam algoritma ini, kita hanya menggunakan tiga kali iterasi (perulangan).
∕π÷1 = ∕π (j^) ^reflect(PSF) = (3)
Nilai fn dikonvolusikan dengan nilai PSF sebagai langkah pertama dalam iterasi pertama operasi algoritma ini. Kemudian, nilai g dibagi dengan hasil konvolusi nilai fn dengan PSF, seperti yang ditunjukkan oleh rumus yang terlihat , Iterasi pertama algoritma ini digambarkan sebagai berikut:
|
221 |
216 |
199 |
179 |
171 | |
|
181 |
ISO |
172 |
159 |
156 |
0.1096 0.1118 0.1096 |
|
139 |
144 |
142 |
135 |
135 |
. 0.1118 0.1141 0.1118 |
|
120 |
129 |
131 |
124 |
121 |
0.1096 0.1118 0.1096 |
|
255 |
255 |
255 |
250 |
242 |
/(1J) = ∣O.IO96.199] + ∣01118∙ 179] + [0.1096 • 171] + [0.1118 « 172| + |0.1141 ■ 159] + [0L1118 • 156] + ∣0.1D96 • 142∣+ [0.1118« 135] + |0.1096 * 135| = 1605287 = Ibl
|
221 |
216 |
199 |
179 |
171 | ||||
|
181 |
ISO |
172 |
159 |
156 |
0.1096 |
0.1118 |
0.1096 | |
|
139 |
144 |
142 |
135 |
135 |
U |
0.1118 |
0.1141 |
0.1118 |
|
120 |
129 |
131 |
124 |
121 |
0.1096 |
0.1118 |
0.1096 | |
|
255 |
255 |
255 |
250 |
242 | ||||
/(2.1) = [0.1096. 181] + (0.1 IlB - 18 0] + [0.1096 - 172] + [O.111B ∙ 13 9∣ + [0L1141 « 144∣ + ∣0.1118 * M2| + ∣0.1D96 • 120∣+ ∣O.Π1B* 129] + [0L1096< 131| = 1485908= 148
|
221 |
216 |
199 |
179 |
171 | |
|
181 |
ISO |
172 |
159 |
156 |
0.1096 0.1118 0.1096 |
|
139 |
144 |
142 |
135 |
135 |
• 0.1118 0.1141 0.1118 |
|
120 |
129 |
131 |
124 |
121 |
0.1096 0.1118 0.1096 |
|
1-255 |
255 |
255 |
250 |
242 |
/(Z2) = [0.1096 > 180∣+[01118> 172] + [0.1096 • 159] + [0.1118 « 144| + |0.1141 * 142| + |0.1118 • 135]
+ ∣0.1096> 129∣+ ∣0.111B' 131∣ +10.1096 . 124| = 146.153 = 146
|
221 |
216 |
199 |
179 |
171 | |
|
181 |
180 |
172 |
159 |
156 |
0.1096 0.1118 0.1096 |
|
139 |
144 |
142 |
135 |
135 |
* 0.1118 0.1141 0.1118 |
|
120 |
129 |
131 |
124 |
121 |
0.1096 0.1118 0.1096 |
|
255 |
255 |
255 |
250 |
242 |
/(23) = [0.1096. 1721+|0.1118> 159]+[0.1096* 156]+ [0.1118* 142] +[0L1141 * 135] +[OLl 118 • 135)
+ [0.1096* 131∣+ ∣0.111B. 124∣ +10.1096. 121) = 1415795 = 141
|
221 |
216 |
199 |
179 |
171 | |
|
181 |
ISO |
172 |
159 |
156 |
0.1096 0.1118 0.1096 |
|
139 |
144 |
142 |
135 |
135 |
• 0.1118 0.1141 0.1118 |
|
120 |
129 |
131 |
124 |
121 |
0.1096 0.1118 0.1096. |
|
255 |
255 |
255 |
250 |
242 |
|
r-" = A {; |
l-pjJ-,c^m |
= | ||||||||
|
f221 |
216 |
199 |
179 |
L 71 | ||||||
|
181 |
IBO |
172 |
L59 |
L 56 |
0.1096 |
IJlllB |
D 1096 | |||
|
139 |
144 |
142 |
L35 |
L35 |
■ |
Oiim |
0.1141 |
D I I Kl | ||
|
120 |
129 |
131 |
L24 |
L2.L |
0.1096 |
o.iiin |
0 1096 | |||
|
∣-255 |
255 |
255 |
250 |
242 | ||||||
/(Ll) = ∣Q.1D96∙221∣ +[0.1118* 216∣+∣O.1D96> 199] + [0.1118 * 181∣ + ∣0.1141 • 180] + [OLlllB * I72| + ∣0.1D96 • 139∣+ ∣0.111B* 144] + [0L1096∙ 142∣ = 177.0B1 = 177
|
'221 |
216 |
199 |
179 |
L 71 | |
|
IBl |
IBO |
172 |
159 |
L 56 |
'O. 1096 O.llin 0 1096 |
|
139 |
144 |
142 |
135 |
L35 |
I O.llin 0.1141 DLJJiI |
|
120 |
129 |
131 |
124 |
121 |
.0.1096 O.llin 0 1096 |
|
⅛55 |
255 |
255 |
250 |
242 |
f(12) =[0.1096*216]+ [0.1118« 199] + [0.1096« 179∣ + ∣0.1118 * 1BO∣ + [0.1141 *
-
172] +∣0.il 18- 159∣ + ∣0.1096> 144] + [0.1118* 142] + [0.1096 • 135]= 169.5196 =169
/(3.i) = |0JD96> 139]+ [ftlllβ" 144] HQlLIHf' 1*2] + ∣∏ 11 Lfi ■ ESQ]+[0.11*1 ■ LM] + ∣0 IJ IB * I3L∣ ÷ ∣Π.JD⅛6- 2 5Ξ∣ + ∣II IlLI?' 2 5Ξ∣ + ∣DL1096 ■ 2 55∣l = I71.OB25 = 17
|
221 IBI |
216 IfiD |
159 172 |
179 159 |
L7L 1156 |
IQlUHf |
OJliS |
D 1096 |
|
Ififi |
144 |
142 |
135 |
IlSS |
> Q.ιιιn |
QJ 1*1 |
Dlll-I |
|
120 |
129 |
LIl |
124 |
121 |
∣QHN6 |
OJllS |
D 1096 |
|
⅛55 |
255 |
255 |
2 50 |
242 |
/(3.2) = ∣0JD9⅛ - J44∣ + ∣ft.]∣mh 1*2] -∣O.1DM- L35∣ - ∣∏ I IJG - 129] + [ILl L *1 ■ 13 L∣ + [ILlLlB ■ LMj HQllfififi* 25Ξ∣ + Ir: IJLI?'- 25Ξ∣ + ∣DL109b- 250]= 173^435 = 173
|
221 ISll |
216 JlfiQ |
199 172 |
179 159 |
171 156 |
IQllOH |
OJllS |
O 1096 |
|
139 |
L44 |
L42 |
139 |
JlS |
i OlILlfi |
OJ141 |
D I I Kl |
|
120 |
129 |
LJl |
124 |
131 |
IjOJDM |
OJllS |
D 1096 |
|
⅛55 |
255 |
255 |
2 50 |
2 12 |
/(3J) = ∣0JD9⅛ - J42] + ∣Q.]∣l∏b IfitfHQHJHf- L35∣ - ∣∏ I I IB∏ 131J-∣DL1J4I ■ 12*]+[0.1113' L21∣ Mθ.lD9fi- 25Ξ∣ + [Qltllfi- 25O∣ - ∣∣) 1096 ^ 2l2∣ = 170r19M = 170
Pengkonvolusiannya sama dengan yang disebutkan di atas, jadi dari pengkonvolusi ini dapat diperoleh nilai hasil berikut:
|
221 |
216 |
199 |
179 |
171I |
|
IBl |
177 |
L 1:9 |
IGI |
156 |
|
IW |
1*0 |
146 |
14 L |
135 |
|
120 |
174 |
173 |
170 |
I2L |
|
255 |
255 |
255 |
25 ∏ |
242-∣ |
Nilai g dibagi dengan nilai hasil konvolusi sebelumnya , di langkah berikutnya.
Prosedurnya adalah sebagai berikut:
|
r221 |
216 |
199 |
179 |
171-1 |
|
181 |
180 |
172 |
159 |
156 |
|
139 |
144 |
142 |
135 |
135 |
|
120 |
129 |
131 |
124 |
121 |
|
1-255 |
255 |
255 |
250 |
242-1 |
|
r221 |
216 |
199 |
179 |
1711 |
|
181 |
177 |
169 |
161 |
156 |
|
139 |
148 |
146 |
141 |
135 |
|
120 |
174 |
173 |
170 |
121 |
|
∣-255 |
255 |
255 |
250 |
242-∣ |
Dari pembagian diatas maka didapat nilai hasil sebagai berikut:
Illll Illll Illll Illll Illll
Setelah itu, hasil output pertama kali dikalikan dengan nilai fn. Nilai yang dihasilkan dari perkalian
|
r221 |
216 |
199 |
179 |
171I |
■i |
1 |
L |
1 |
1 | |
|
181 |
180 |
172 |
159 |
156 |
1 |
1 |
1 |
1 |
1 | |
|
139 |
144 |
142 |
135 |
135 |
X |
1 |
1 |
1 |
L |
1 |
|
120 |
129 |
131 |
124 |
121 |
1 |
1 |
1 |
1 |
1 | |
|
⅛5 |
255 |
255 |
250 |
242-∣ |
■1 |
1 |
1 |
1 |
1 |
di atas adalah sebagai berikut:
|
r221 |
216 |
199 |
179 |
171I |
|
181 |
180 |
172 |
159 |
156 |
|
139 |
144 |
142 |
135 |
135 |
|
120 |
129 |
131 |
124 |
121 |
|
•■255 |
255 |
255 |
250 |
242j |
Setelah menghitung nilai output, langkah selanjutnya adalah mengubah nilai hasil tersebut dengan nilai reflect(PSF), yang dilakukan dengan cara berikut:
|
221 181 |
216 180 |
199 172 |
179 159 |
171 156 |
10.1096 |
0.1118 |
0.1096 |
|
139 |
144 |
142 |
135 |
135 |
* 0.1118 |
0.1141 |
0.1118 |
|
120 |
129 |
131 |
124 |
121 |
10.1096 |
0.1118 |
0.1096 |
|
255 |
255 |
255 |
250 |
242J |
/(1.1) = [0.1096» 221]+ [0.1110>216] + [0.1096» 1991 + [01118* 181] + [0.1141 « 180] + [0.1 IlH » 172] + [0.1096 « 139] + [0.1118 « 144] + [0.1096 * 142] = 177.0H1 = 177
|
221 IHl |
216 180 |
199 172 |
179 159 |
171 156 |
10.1096 |
0.1118 |
0.1096 |
|
139 |
144 |
142 |
135 |
135 |
> 0.1118 |
0.1141 |
0.1118 |
|
120 |
129 |
131 |
124 |
121 |
10.1096 |
0.1118 |
0.1096 |
|
255 |
255 |
255 |
250 |
242J |
/(12) = [0.1096*216]+ [0.1118* 199] + [0.1096 » 179[ + [0.1118 » 180]+ [0.1141 * 172] + [0.1 IlH * 159] + [0.1096 * 144] + [0.1118 * 142] + [0.1096 * 135] = 169.5196 = 169
|
221 IHl |
216 180 |
199 172 |
179 159 |
171 156 |
[0.1096 |
0.1118 |
0.1096 |
|
139 |
144 |
142 |
135 |
135 |
> 0.1118 |
0.1141 |
0.1118 |
|
120 |
129 |
131 |
124 |
121 |
∣03096 |
0.1118 |
0.1096 |
|
255 |
255 |
255 |
250 |
242-∣ |
/(13) = [0.1096* 199]+ [0.1118* 179] + [0.1096* 171) + [0.1118* 172] + [0.1141 * 159] + [0.1 IlH * 156] + [0.1096 * 142] + [0.1118 « 135] + [0.1096 » 135] = 160.8287 = 161
|
221 181 |
216 180 |
199 172 |
179 159 |
171 156 |
[0.1096 |
0.11 IH |
0.1096 |
|
139 |
144 |
142 |
135 |
135 |
> 0.1118 |
0.1141 |
0.1118 |
|
120 |
129 |
131 |
124 |
121 |
10.1096 |
0.11 IH |
0.1096 |
|
255 |
255 |
255 |
250 |
242∣ |
/(2.1) = [0.1096* 1H1] + [0.1118* 180] + [0.1096 * 172] + [0.1118 * 139]+ [0.1141 * 144] + [0.111H • 142] + [0.1096 * 120] + [0.1118 » 129] + [0.1096 * 131] = 148.5908 = 148
|
221 IHl |
216 180 |
199 172 |
179 159 |
171 156 |
[0.1096 |
0.1118 |
0.1096 |
|
139 |
144 |
142 |
135 |
135 |
> 0.1118 |
0.1141 |
0.1118 |
|
120 |
129 |
131 |
124 |
121 |
lθ,!O96 |
0.11 IH |
0.1096 |
|
255 |
25 5 |
255 |
250 |
242∣ |
/(22) = [0.1096* 180] + [0.1118* 172] + [0.1096 * 159] + [0.1118 * 144] + [0.1141 * 142] + [0.111H * 135] + [0.1096 * 129] + [0.1118 « 131] + [0.1096 * 124] = 146.153 = 146
|
221 IHl |
216 180 |
199 172 |
179 159 |
171 156 |
[0.1096 |
0.11 IH |
0.1096 |
|
139 |
144 |
142 |
135 |
135 |
> IoillH |
0.1141 |
0.1118 |
|
120 |
129 |
131 |
124 |
121 |
10-1096 |
0.111H |
0.1096 |
|
255 |
255 |
255 |
250 |
242-∣ |
/(23) = [0.1096 * 172] + [0.1118 * 159] + [0.1096 * 156] + [0.1118 * 142] + [0.1141 * 135] + [0.111H * 135] + [0.1096 » 131] + [0.1118 » 124] + [0.1096 » 121] = 141.5795 = 141
|
221 181 |
216 180 |
199 172 |
179 159 |
171 156 |
[0.1096 |
0.11 IH |
0.1096 |
|
139 |
144 |
142 |
135 |
135 |
* 0.1118 |
0.1141 |
0.1118 |
|
120 |
129 |
131 |
124 |
121 |
∣0l1096 |
0.11 IH |
0.1096 |
|
255 |
255 |
255 |
250 |
242j |
/(3.1) = (0.1096* 139] + [0.1118* 144] + [0.1096 • 142] + [0.1118 • 120]+ [0.1141 « 129] + [0.1 IlH - 131] + [0.1096 * 255] + [0.1118 » 255] + [0.1096 * 255] = 174,0825 = 174
|
221 IHl |
216 180 |
199 172 |
179 159 |
171 156 |
[0.1096 |
0.11 IH |
0.1096 |
|
139 |
144 |
142 |
135 |
135 |
* 0.1118 |
0.1141 |
0.1118 |
|
120 |
129 |
131 |
124 |
121 |
∣0l1096 |
O-IllH |
0.1096 |
|
255 |
255 |
255 |
250 |
242∣ |
/(3^) = [OJD⅜∙ 144] + [0.1118* 142] + 10.1096 * 135] + [0.1118 » 129] + [0.1141 * 131]+ [0.1118 ∙ 124] + [0.1096 » 255] + [0.1118 ∙ 255) + [Ol1O96 * 250] = 1735435 = 173
|
221 |
216 |
199 |
179 |
171 | |||
|
IHl |
180 |
172 |
159 |
156 |
10.1096 |
0.1118 |
0.1096 |
|
139 |
144 |
142 |
135 |
135 |
« 0.1118 |
0.1141 |
0.1118 |
|
120 |
129 |
131 |
124 |
121 |
10.1096 |
0.1118 |
0.1096 |
|
255 |
255 |
255 |
250 |
242 |
/(33) = [0.1096» 142] + [0.1118» 135] + [0.1D96 » 135] + [0.1118 » 131] + [0.1141 « 124] + [O.IllH » 121] + [0.1096 » 255] + [0.1118 » 250] + [0.1096 * 242] = 170,1954 = 170
Nilai output /1 yang dihasilkan dari perhitungan konvolusi nilai fn dengan nilai pencerminan (PSF) adalah sebagai berikut:
Iterasi kedua:
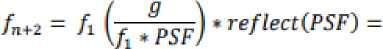
(4)
Langkah iterasi kedua dan pertama sama saja, kecuali nilai f1 diambil dari nilai hasil langkah iterasi sebelumnya.
|
221 181 |
216 177 |
199 169 |
179 161 |
171 156 |
10.1096 |
0.1118 |
0.1096 |
|
139 |
148 |
146 |
141 |
135 |
• 0.1118 |
0.1141 |
0.1118 |
|
120 |
174 |
173 |
170 |
121 |
10.1096 |
0.1118 |
0.1096 |
|
■255 |
255 |
255 |
250 |
242 |
Hasil dari konvolusi di atas adalah sebagai berikut:
|
221 |
216 |
199 |
179 |
171 |
221 |
216 |
199 |
179 |
171 | |
|
181 |
177,2889 |
170,6087 |
161,8307 |
156 |
181 |
177 |
170 |
162 |
156 | |
|
139 |
158,4644 |
161,9516 |
152,3521 |
135 |
= |
139 |
159 |
162 |
153 |
135 |
|
120 |
184,7982 |
184,5745 |
181,2488 |
121 |
120 |
185 |
185 |
182 |
121 | |
|
255 |
255 |
255 |
250 |
242- |
■255 |
255 |
255 |
250 |
242 |
Nilai g dibagi dengan nilai hasil output konvolusi sebelumnya dalam langkah berikutnya. Prosedurnya adalah sebagai berikut:
|
221 |
216 |
199 |
179 |
171 |
|
ISl |
180 |
172 |
159 |
156 |
|
139 |
144 |
142 |
135 |
135 |
|
120 |
129 |
131 |
124 |
121 |
|
hss |
255 |
255 |
250 |
242-∣ |
|
221 |
216 |
199 |
179 |
171 |
|
ISl |
177 |
170 |
162 |
156 |
|
139 |
159 |
162 |
153 |
135 |
|
120 |
185 |
185 |
182 |
121 |
|
l255 |
255 |
255 |
250 |
242j |
Dari pembagian diatas maka didapat nilai hasil sebagai berikut:
Illll
Illll
Illll
Illll
Illll
Setelah itu, hasil output pertama kali dikalikan dengan nilai /1.
|
r221 |
216 |
199 |
179 |
171I |
■i |
1 |
L |
1 |
1 | |
|
181 |
180 |
172 |
159 |
156 |
1 |
1 |
1 |
1 |
1 | |
|
139 |
144 |
142 |
135 |
135 |
X |
1 |
1 |
1 |
1 |
1 |
|
120 |
129 |
131 |
124 |
121 |
1 |
1 |
1 |
1 |
1 | |
|
⅛5 |
255 |
255 |
250 |
242^ |
■1 |
1 |
1 |
1 |
1 |
Nilai yang dihasilkan dari perkalian di atas adalah sebagai berikut:
Setelah menghitung nilai output, langkah selanjutnya adalah mengubah nilai hasil tersebut dengan nilai reflect(PSF), yang dilakukan dengan cara berikut:
Nilai output f2 dihasilkan dari perhitungan konvolusi nilai f1 dengan nilai pencerminan (PSF)
|
221 |
216 |
199 |
179 |
171 | |
|
181 |
177 |
169 |
161 |
156 |
0.1096 0.1118 0.109 6 |
|
139 |
L 4 R |
146 |
141 |
135 |
4 DLlllS 0.1141 0.1 UR |
|
120 |
174 |
173 |
170 |
121 |
0.1096 0.1118 0.1096 |
|
■255 |
255 |
255 |
250 |
242 |
sebagai berikut:

|
221 |
216 |
199 |
179 |
171 |
221 |
216 |
199 |
179 |
171 | |
|
181 |
177,2889 |
17D,60H7 |
161,8307 |
156 |
181 |
177 |
170 |
162 |
156 | |
|
139 |
158,4644 |
161,9516 |
152,3521 |
135 |
= |
139 |
159 |
162 |
153 |
135 |
|
120 |
181,7982 |
190,0527 |
181,2488 |
121 |
120 |
182 |
191 |
182 |
121 | |
|
255 |
255 |
255 |
250 |
242- |
255 |
255 |
255 |
250 |
242 |
Iterasi ketiga:
Langkah iterasi ketiga identik dengan langkah pertama dan kedua. untuk alasan bahwa algoritma Lucy-Richardson adalah algoritma perulangan. Oleh karena itu, kita hanya dapat mengulangi algoritma ini sebanyak yang kita inginkan. Namun, saya hanya akan mencoba tiga kali di sini.
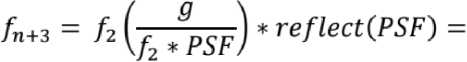
Jurnal Nasional Teknologi Informasi dan Aplikasinya
|
r221 |
216 |
199 |
179 |
171I | ||||
|
181 |
177 |
170 |
162 |
156 |
0.1096 |
0.1118 |
0.1096 | |
|
139 |
159 |
162 |
153 |
135 |
* |
0.1118 |
0.1141 |
0.1118 |
|
120 |
182 |
191 |
182 |
121 |
0.1096 |
0.1118 |
0.1096 | |
|
∣-255 |
255 |
255 |
250 |
242^ | ||||
Hasil dari konvolusi di atas adalah sebagai berikut:
|
221 |
216 |
199 |
179 |
171 |
221 |
216 |
199 |
179 |
171" | |
|
181 |
180,3841 |
175,1442 |
165,1518 |
156 |
181 |
180 |
175 |
166 |
156 | |
|
139 |
164,4851 |
170,7744 |
159,0459 |
135 |
= |
139 |
165 |
171 |
160 |
135 |
|
120 |
190,7068 |
198,6521 |
187,7256 |
121 |
120 |
191 |
199 |
188 |
121 | |
|
-255 |
255 |
255 |
250 |
242 |
255 |
255 |
255 |
250 |
242- |
Nilai g dibagi dengan nilai hasil output konvolusi sebelumnya dalam langkah berikutnya, yang langkah-langkahnya adalah sebagai berikut:
|
221 |
216 |
199 |
179 |
171 |
|
181 |
180 |
172 |
159 |
156 |
|
139 |
144 |
142 |
135 |
135 |
|
120 |
129 |
131 |
124 |
121 |
|
-255 |
255 |
255 |
250 |
242 |
|
221 |
216 |
199 |
179 |
171 |
|
181 |
180 |
175 |
166 |
156 |
|
139 |
165 |
171 |
160 |
135 |
|
120 |
191 |
199 |
188 |
121 |
|
255 |
255 |
255 |
250 |
242 |
Dari pembagian diatas maka didapat nilai hasil sebagai berikut:
Illl 1 Illll Illll
Illll Illl 1
Setelah itu, hasil output pertama kali dikalikan dengan nilai f2.
Nilai yang dihasilkan dari perkalian di atas adalah sebagai berikut:
|
r221 |
216 199 |
179 |
171I |
rl 1 |
1 |
1 |
1 |
|
181 |
180 172 |
159 |
156 |
1 1 |
1 |
1 |
1 |
|
139 |
144 142 |
135 |
135 |
xll |
1 |
1 |
l |
|
120 |
129 131 |
124 |
121 |
1 1 |
1 |
1 |
1 |
|
⅛5 |
255 255 |
250 |
242^ |
h i |
1 |
1 |
1 |
|
r221 |
216 |
199 |
179 171-∣ | ||||
|
181 |
180 |
172 |
159 156 | ||||
|
139 |
144 |
142 |
135 135 | ||||
|
120 |
129 |
131 |
124 121 | ||||
|
∣-255 |
255 |
255 |
250 242j |
Setelah menghitung nilai output, langkah selanjutnya adalah mengubah nilai hasil tersebut dengan nilai reflect(PSF), yang dilakukan dengan cara berikut:
|
221 |
216 |
199 |
179 |
171' | ||||
|
181 |
180 |
175 |
166 |
156 |
0.1096 |
0.1118 |
0.1096 | |
|
139 |
165 |
171 |
160 |
135 |
* |
0.1118 |
0.1141 |
0.1118 |
|
120 |
191 |
199 |
188 |
121 |
.0.1096 |
0.1118 |
0.1096. | |
|
-255 |
255 |
255 |
250 |
242- | ||||
Nilai output f3 dihasilkan dari perhitungan konvolusi nilai f2 dengan nilai pencerminan (PSF) sebagai berikut:
|
•221 181 |
216 182,9426 |
199 178,9283 |
179 167,9362 |
171' 156 |
'221 181 |
216 182 |
199 178 |
179 168 |
171’ 156 | ||
|
= 139 |
168,9423 |
177,1193 |
162,7228 |
135 |
= |
139 |
169 |
178 |
163 |
135 | |
|
120 |
194,2853 |
203,6729 |
191,0736 |
121 |
120 |
195 |
204 |
192 |
121 | ||
|
255 |
255 |
255 |
250 |
242^ |
255 |
255 |
255 |
250 |
242- | ||
|
221 |
216 |
199 |
179 |
171 | |||||||
|
181 |
182 |
178 |
168 |
156 | |||||||
|
139 |
169 |
178 |
163 |
135 | |||||||
|
120 |
195 |
204 |
192 |
121 | |||||||
|
255 |
255 |
255 |
250 |
242 | |||||||
Ada beberapa kesimpulan yang dapat diambil dari penulisan dan analisis bab-bab sebelumnya. Kesimpulannya adalah bahwa proses perbaikan kualitas gambar dapat bekerja dengan baik untuk mengurangi noise gaussian blur. Restoration Image bertujuan untuk menghilangkan atau mengurangi kerusakan gambar. Tujuannya hampir sama dengan operasi perbaikan gambar, tetapi penyebab kerusakan gambar sudah diketahui. Untuk merestorasi image, Metode Lucy-Richardson salah satu metode yang dapat digunakan untuk melakukan image restoration pada citra digital. Metode ini didasarkan pada konsep dekonvolusi, yaitu proses untuk memperbaiki citra yang terkena blur atau noise dengan menghilangkan efek blur atau noise tersebut. Metode Lucy-Richardson dapat digunakan untuk membuat aplikasi perbaikan kualitas gambar.
Daftar Pustaka
-
[1] P. Danoedoro, Pengantar Penginderaan Jauh Digital, 1st Ed. Yogyakarta: Andi, 2012.
-
[2] R. Munir, “Restorasi Citra Kabur Dengan Algoritma,” Semin. Nas. Apl. Teknol. Inf., Vol. 2006, No. Snati, 2006
-
[3] Dwisa Elma Yuni. (2019) “Aplikasi Pengenalan Tajwid Menggunakan Pengelolahan Citra Digital Berbasis Multimedia,” Skripsi Sarjana,Universitas Islam Riau, 2019.
-
[4] Kasman Rukun, Asrul Huda, Dan Yeka Hendriyani. “Rancang Bangun Cd Interaktif Pembelajaran Pengolahan Citra Digital Berbasis Multimedia Dengan Model Classic Tutorial,” In Jurnal Nasional Pendidikan Teknik Informatika (Janapati), 2016, Vol. 2016-Juli
366
Discussion and feedback