Pengklusteran Data Iris Menggunakan Metode Fuzzy C-Means
on
JNATIA Volume 2, Nomor 2, Februari 2024
Jurnal Nasional Teknologi Informasi dan Aplikasinya
p-ISSN: 2986-3929
Pengklusteran Data Iris Menggunakan Metode Fuzzy C-Mean
Gde Krishna Sankya Yogeswaraa1
aProgram Studi Informatika, Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Udayana, Bali
Jln. Raya Kampus UNUD, Bukit Jimbaran, Kuta Selatan, Badung, 08261, Bali, Indonesia 1krishnasankya@gmail.com
Abstract
This study focuses on the application of the Fuzzy C-Means method for clustering the Iris dataset. Clustering is a widely used technique for grouping similar data objects together, and the Iris dataset, which consists of measurements of iris flowers, has been a popular choice for clustering analysis. The Fuzzy C-Means algorithm, based on fuzzy logic, allows for a more flexible and nuanced approach to clustering by assigning degrees of membership to data points, capturing the inherent uncertainty and ambiguity in the dataset. By utilizing fuzzy logic, the Fuzzy C-Means method aims to accurately classify iris flowers into distinct clusters based on their petal width, petal length, sepal width, and sepal length. The results of this study contribute to the understanding of fuzzy clustering techniques and their application in pattern recognition and data analysis.
Keywords: Iris dataset, clustering, Fuzzy C-Means, fuzzy logic.
Indonesia memiliki kekayaan sumber daya alam yang melimpah, sehingga negara ini memiliki beragam tumbuhan dan bunga yang tersebar di seluruh wilayahnya. Meskipun demikian, hanya sekitar 20% dari total tumbuhan di Indonesia yang telah diidentifikasi [1]. Secara umum, tanaman yang belum diidentifikasi sering diklasifikasikan atau dikelompokkan ke dalam beberapa kelompok. Pengklasteran atau pengelompokkan adalah proses mengelompokkan objek atau kasus ke dalam kelompok-kelompok yang lebih kecil, di mana setiap kelompok berisi objek atau kasus yang memiliki kesamaan satu sama lain [2]. Data iris sering digunakan untuk melakukan pengklasteran berbagai jenis bunga berdasarkan lebar mahkota (petal width), panjang mahkota (petal length), lebar kelopak (sepal width), dan panjang kelopak (sepal length).
Data iris adalah kumpulan data yang terdiri dari bunga yang diidentifikasi berdasarkan ukuran panjang mahkota, lebar mahkota, panjang kelopak, dan lebar kelopaknya [3]. Sebelumnya, banyak peneliti telah menggunakan data iris sebagai sarana untuk menguji metode pengklasteran. Data iris dipilih karena sederhana dan mudah diperoleh. Terdapat beberapa metode yang digunakan untuk mengelompokkan data menjadi beberapa kelompok, salah satunya adalah dengan memanfaatkan cabang ilmu matematika seperti data mining dan logika fuzzy.
Logika fuzzy merupakan salah satu cabang ilmu matematika yang fokus pada konsep logika yang kabur atau tidak tegas. Logika fuzzy menggunakan rentang keanggotaan antara 0 dan 1, berbeda dengan logika klasik yang hanya memiliki nilai keanggotaan 0 atau 1. Logika fuzzy sering dianggap sebagai kotak hitam yang menghubungkan ruang input dengan ruang output. Penggunaan himpunan fuzzy membantu mengatasi keterbatasan himpunan crisp yang terkadang kurang adil. Dalam himpunan crisp, perubahan kecil dalam nilai batas dapat menyebabkan perbedaan kategori yang signifikan. Dengan menggunakan himpunan fuzzy, perubahan kecil tersebut dapat diantisipasi dan kategori yang lebih akurat dapat ditentukan [4].
Pada penelitian ini akan dilakukan pengklusteran data iris dengan cara melakukan pengukuran berdasarkan lebar mahkota (petal width), panjang mahkota (petal length), lebar kelopak (sepal width), dan panjang kelopak (sepal length). Dalam hal ini, pengklasteran dilakukan untuk mengelompokkan bunga-bunga berdasarkan karakteristik tersebut.
Dalam jurnal ini, dilakukan pengklasteran data iris menggunakan metode, yaitu metode fuzzy c-means. Sebagaimana dijelaskan pada bab sebelumnya mengenai algoritma metode tersebut. Untuk memahami metode fuzzy c-means dapat dilihat dari flowchart algoritma, gambar 1. Tahapan penelitian merupakan ilustrasi langkah- langkah metode yang akan dikerjakan.
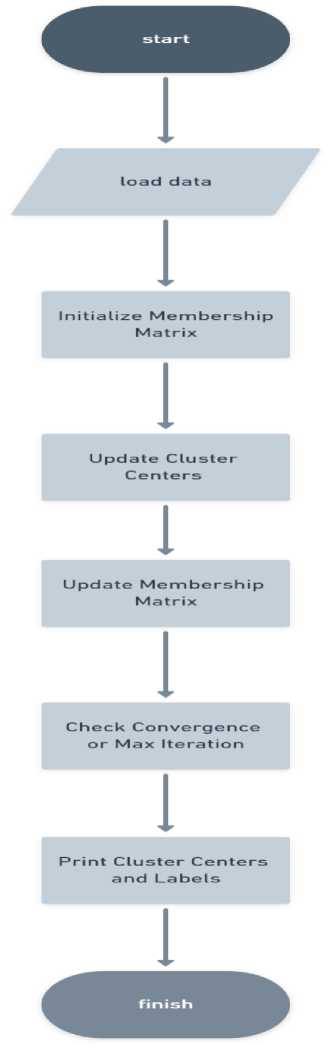
Gambar 1. Alur Logika Fuzzy
Gambar 1. Ini menggambarkan langkah-langkah utama dalam algoritma Fuzzy C-Means untuk pengklasteran data iris. Program dimulai dengan memuat data dari file CSV, kemudian melakukan inisialisasi matriks keanggotaan. Selanjutnya, program melakukan pembaruan pusat kluster dan matriks keanggotaan secara berulang sampai mencapai konvergensi atau mencapai batas iterasi maksimum yang ditentukan. Setelah itu, program mencetak pusat kluster dan label kluster untuk setiap sampel data iris sebelum akhirnya berakhir.
Logika fuzzy merupakan seuatu logika yang memiliki nilai kekaburan atau kesamaran (fuzziness) antara benar atau salah. Logika Fuzzy pertama kali diperkenalkan oleh Prof. Lotfi A. Zadeh pada tahun 1965. Dalam teori logika fuzzy suatu nilai bias bernilai benar atau salah secara bersama. Namun berapa besar keberadaan dan kesalahan suatu tergantung pada bobot keanggotaan yang dimilikinya. Logika fuzzy memiliki derajat keanggotaan dalam rentang 0 hingga 1. Berbeda dengan logika digital yang hanya memiliki dua nilai 1 atau 0. Logika fuzzy digunakan untuk menterjemahkan suatu besaran yang diekspresikan menggunakan bahasa (linguistic), misalkan besaran kecepatan laju kendaraan yang diekspresikan dengan pelan, agak cepat, cepat, dan sangat cepat. Dan logika fuzzy menunjukan sejauh mana suatu nilai itu benar dan sejauh mana suatu nilai itu salah. Tidak seperti logika klasik (crisp)/ tegas, suatu nilai hanya mempunyai 2 kemungkinan yaitu merupakan suatu anggota himpunan atau tidak. Derajat keanggotaan 0 (nol) artinya nilai bukan merupakan anggota himpunan dan 1 (satu) berarti nilai tersebut adalah anggota himpunan [5].
Penelitian ini menggunakan dataset Pengelompokan pada Dataset Iris terkait dengan latar belakang yang didapat dari platform kaggle.
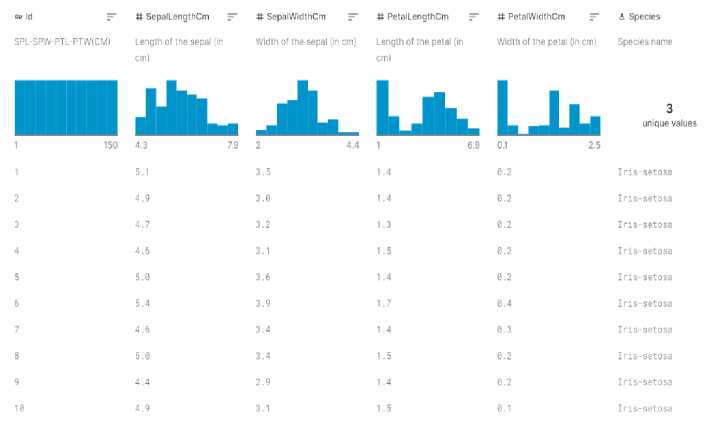
Tahap ini bertujuan untuk memastikan integritas data sehingga nantinya tidak menimbulkan masalah pada proses data training atau pelatihan data. data iris yang digunakan terbagi menjadi 4 kelas yaitu berdasarkan lebar mahkota (petal width), panjang mahkota (petal length), lebar kelopak (sepal width), dan panjang kelopak (sepal length).
Pada tahap ini, Setelah dijalankan, pengklasteran akan menghasilkan kelompok-kelompok data. Kelompok-kelompok data ini dapat direpresentasikan dalam bentuk grafik. Dengan demikian, dapat dilihat sebaran data pada setiap klaster berdasarkan kedekatannya dengan pusat klaster, hal tersebut terlihat seperti pada gambar 3. dan gambar 4.
Sepal Plot
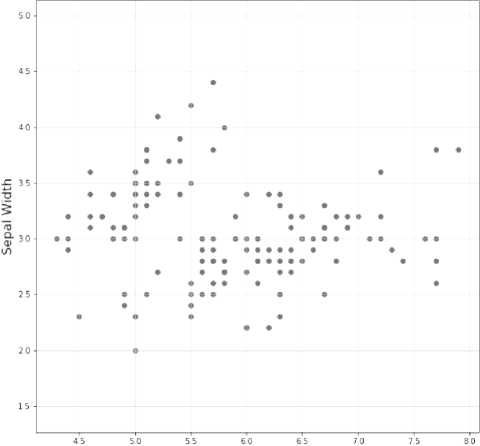
Sepal Length
Gambar 3. Sebaran Data 1
Petal Plot
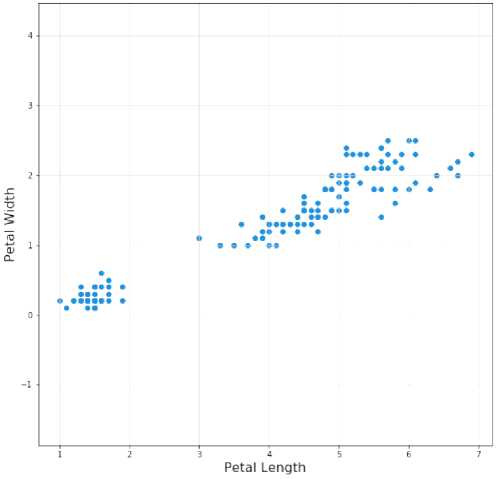
Gambar 4. Sebaran Data 2
Cluster Centers:
[[6.77506153 3.05241419 5.64684284 2.0535809 ]
[5.8891523 2.76121785 4.3641857 1.39741075]
[5.00356122 3.40303794 1.4849977 0.25153934]]
Labels:
[2 222222222222222222222222222222222222 2222222222222Θ10111111111111111111111 1110111111111111111111111101000010000 001ΘΘ00Θ101010011000Θ01Θ0001Θ0010001Θ θ 1]
Gambar 5. Cluster Center
Hasil akhir atau output program di atas mencetak dua hal: "Cluster Centers" dan "Labels".
-
1. "Cluster Centers": Bagian ini mencetak matriks pusat kluster yang dihasilkan setelah
menjalankan algoritma Fuzzy C-Means pada data iris. Setiap baris dalam matriks ini mewakili koordinat pusat kluster untuk kluster tertentu. Dalam contoh ini, matriks pusat kluster memiliki dimensi ` (n_clusters, X.shape[1])`, di mana `n_clusters` adalah jumlah kluster yang ditentukan dan `X.shape[1]` adalah jumlah fitur dalam data iris.
-
2. "Labels": Bagian ini mencetak label kluster untuk setiap sampel data iris. Label kluster
menunjukkan keanggotaan setiap sampel dalam kluster tertentu. Pada titik ini, label kluster dihitung berdasarkan indeks kluster dengan nilai keanggotaan terbesar untuk setiap sampel. Hasil ini adalah array dengan panjang sama dengan jumlah sampel dalam data iris.
Jadi, hasil akhir dari program ini memberikan informasi tentang pusat kluster yang dihasilkan dan label kluster untuk setiap sampel data iris. Dengan demikian, kita dapat melihat lokasi pusat kluster dan bagaimana data iris dikelompokkan dalam kluster-keluster tersebut.
Dalam penelitian ini, metode Fuzzy C-Means berhasil diterapkan untuk pengklusteran data iris. Metode ini mampu mengelompokkan bunga iris berdasarkan karakteristik lebar mahkota (petal width), panjang mahkota (petal length), lebar kelopak (sepal width), dan panjang kelopak (sepal length) dengan menggunakan konsep logika fuzzy. Penggunaan logika fuzzy memungkinkan adanya derajat keanggotaan antara 0 dan 1, sehingga dapat menggambarkan tingkat keabuan dan kemungkinan suatu nilai. Dengan menggabungkan informasi keanggotaan dari masing-masing data iris, metode Fuzzy C-Means mampu menghasilkan kluster yang lebih fleksibel dan dapat mengatasi ketidakpastian serta ambiguitas dalam dataset. Hasil pengklusteran ini memberikan pemahaman yang lebih baik mengenai teknik pengelompokan fuzzy dan penerapannya dalam pengenalan pola dan analisis data.
Daftar Pustaka
-
[1] Siregar, Mustaid. Jumlah Spesies Tumbuhan Flora di Indonesia, diambil dari http://www.lipi.go.id/, pada tanggal 8 Juni 2023
-
[2] Kuniawati, Rizki Taher dkk. Pengelompokan Kualitas Udara Ambien Menurut Kabupaten/Kota di Jawa Tengah Menggunakan Analisis Klaster. Jurnal Gaussian, Vol 4 No 2
-
[3] Kadir, Abdul. Identifikasi Tiga Jenis Bunga iris Menggunakan ANFIS.
-
[4] Kusumadewi, Sri dan Purnomo, Hari. Aplikasi Logika Fuzzy untuk pendukung keputusan.
Edisi 2. Yogyakarta. Graha Ilmu.
-
[5] J. Bezdek, Pattern Recognition with Fuzzy Objective Function Algorithm, New York: Plenum Press, 1981.
286
Discussion and feedback