Perancangan Guitar Tuning Berbasis Web
on
JNATIA Volume 2, Nomor 2, Februari 2024 p-ISSN: 2986-3929
Jurnal Nasional Teknologi Informasi dan Aplikasinya
Perancangan Guitar Tuning Berbasis Web
I Nyoman Dheva Suryaa1, Cokorda Rai Adi Pramarthaa2, Agus Muliantarab3
aProgram Studi Informatika, Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Udayana, Bali
Jln. Raya Kampus UNUD, Bukit Jimbaran, Kuta Selatan, Badung, 08261, Bali, Indonesia 1dhevasurya0@gmail.com
2cokorda@unud.ac.id (Corresponding Author)
Abstract
Guitar tuning is a crucial step in preparing for playing, ensuring accurate sound production. In response to this need, our research led to the development of a web-based application dedicated to facilitating precise and straightforward guitar tuning. Leveraging web technology, this application offers users practical tuning experience without the need for additional software installation. By implementing comprehensive tuning features and employing the Fast Fourier Transform (FFT) method, our application guarantees accuracy in detecting and analyzing the spectrum of incoming sound vibrations. This technological approach ensures that users can confidently tune their guitars, avoiding mistuned strings. The decision to create a web-based app aims to optimize device space utilization, as it only requires a standard browser, readily available on all operating systems. In addition to tuning functionality, the application enriches the user experience by providing a collection of guitar chords for each note. This feature enables users to practice and play songs with adjustable transposition and speed. To assess the application's functionality and reliability, we conducted 100 trials using the BlackBox method, focusing on tuning the six guitar strings (e-b-g-d-a-e). The results demonstrated a remarkable 99% accuracy, affirming the system's effectiveness in facilitating precise guitar tuning. In conclusion, our research yields a practical, intuitive, and highly effective web application for users to tune their guitars with confidence and ease.
Keywords: Web, Guitar, Fourier Transform, FFT
Dengan adanya kemajuan teknologi dalam bidang musik, minat untuk mengembangkan dan memperbaiki kemampuan individu semakin tinggi. Namun, proses belajar yang diperlukan untuk menguasai alat musik tertentu membutuhkan waktu yang cukup lama. Selain itu, terbatasnya waktu juga menjadi kendala, ditambah lagi biaya yang harus dikeluarkan untuk mengikuti kursus musik yang tidak murah setiap bulannya. Dalam konteks ini, gitar dipilih sebagai contoh alat musik. Sebagian besar orang mengenal dan mendengar tentang gitar. Namun, mereka yang ingin belajar atau bahkan menjadi mahir dalam memainkannya membutuhkan waktu yang lama untuk menghafal chord yang ada dan chord yang diperlukan dalam sebuah lagu, serta memerlukan biaya yang tidak sedikit untuk mengikuti kursus. Selain itu, mereka juga harus berinteraksi secara teratur dengan guru untuk melatih kemampuan mereka.
Oleh karena itu, penulis memikirkan cara untuk belajar gitar secara mandiri tanpa memerlukan biaya yang tinggi dan harus bertemu guru secara berkala. Dalam hal ini, penulis memilih pengembangan aplikasi berbasis web dengan menggunakan ponsel pintar berbasis Android. Pemilihan ini didasarkan pada fakta bahwa ponsel pintar Android merupakan platform yang bersifat open source dan mudah digunakan, serta fleksibilitas ponsel pintar yang memudahkan pengguna dalam belajar.
Dengan aplikasi "Web Tuning" ini, pengguna dapat dengan mudah mempelajari gitar. Aplikasi ini menyediakan kumpulan chord gitar untuk setiap nada. Pengguna juga dapat memastikan bahwa
setiap senar gitarnya tidak salah dengan menggunakan tuner yang tersedia dalam fitur web ini. Selain itu, pengguna dapat berlatih dengan bermain mini game yang ada dalam aplikasi untuk melatih keterampilan bermain musik mereka, serta berlatih dengan lagu yang dapat diubah nada atau tempo sesuai keinginan. Dengan bantuan Transformasi Fourier Cepat (Fast Fourier Transform/FFT), aplikasi ini dapat mendeteksi dan menganalisis spektrum getaran suara yang masuk. FFT adalah algoritma yang efisien dalam menghitung Transformasi Fourier Diskret (Discrete Fourier Transform/DFT) dan merupakan perhitungan yang mendasar dalam sistem pemrosesan sinyal digital (DSP). Arsitektur FFT telah dipelajari secara luas untuk berbagai aplikasi [2]. Dengan pengembangan aplikasi berbasis web ini, diharapkan para pengguna yang ingin mempelajari gitar dapat dengan mudah belajar. Aplikasi ini memberikan kemudahan dalam mempelajari akor-akor gitar, memastikan penyetelan yang tepat, serta melatih keterampilan bermain musik melalui mini game yang interaktif. Dengan adanya fitur-fitur ini dan penerapan FFT, aplikasi ini dapat membantu pengguna dalam mengembangkan keterampilan musik mereka secara mandiri.
Penelitian ini mengadopsi tiga bagian utama dalam metodologi penelitiannya, yaitu analisis dan desain, implementasi, dan uji coba. Pada tahap analisis dan desain, fokus utama adalah pada perancangan antarmuka serta analisis suara yang akan dikonversi menjadi gelombang frekuensi. Di sisi lain, tahap uji coba melibatkan penggunaan uji coba BlackBox dan penggunaan kuisioner untuk mengumpulkan data.
-
• Nada dan Frekuensi
Nada adalah bunyi yang dihasilkan dari sumber bunyi dengan frekuensi yang teratur [3]. Frekuensi merupakan kecepatan perubahan amplitudo terhadap waktu dan biasanya diukur dalam satuan Hertz (Hz). Frekuensi dapat dihitung berdasarkan jumlah getaran per detik atau jarak relatif antara nada-nada. Terdapat juga tangga nada kromatik yang terdiri dari nada-nada seperti C, C#, D, D#, E, F, F#, G, G#, A, A#, B. Nada memiliki peran penting dalam musik, di mana tinggi rendahnya suara ditentukan oleh frekuensi yang besar atau kecil. Notasi musik digunakan untuk menunjukkan tinggi dan panjang pendeknya nada.
Nada juga merupakan salah satu aspek suprasegmental dalam ujaran, yang ditandai oleh tinggi rendahnya arus ujaran akibat perbedaan frekuensi getaran antara segmen-segmen [Safaat 2016]. Misalnya, ketika seseorang sedih, ucapan mereka cenderung memiliki nada rendah, sementara dalam keadaan marah atau gembira, mereka cenderung menggunakan nada yang tinggi.
Dalam kehidupan sehari-hari, kita dapat menjumpai bunyi yang dihasilkan oleh alat musik seperti gitar, piano, seruling, dan harmonika sebagai contoh konkret dari nada. Nada memiliki tinggi atau deretan nada yang mencakup rentang frekuensi dari yang terendah hingga yang tertinggi, serta interval nada yang menggambarkan perbandingan antara frekuensi nada-nada tersebut.
Tabel 1. Frekuensi Nada Gitar
|
Basis Data |
Notasi Saintis |
Frekuensi |
|
1 |
E5 |
659,26 Hz |
|
2 |
B4 |
493,88 Hz |
|
3 |
G4 |
392,00 Hz |
|
4 |
D4 |
293,00 Hz |
|
5 |
A3 |
220,00 Hz |
|
6 |
E3 |
164,81 Hz |
-
• Kres atau Sharp (#)
Kres atau sharp (#) adalah simbol musik yang digunakan untuk menunjukkan peningkatan satu tingkat tinggi sebuah nada. Ketika sebuah nada diberi tanda kres (#), artinya nada tersebut dimainkan dengan peningkatan setengah langkah dari nada aslinya. Dengan kata lain, kres (#) menaikkan nada sebesar satu interval semitone. Misalnya, jika kita memiliki nada C dan menambahkan tanda kres (#), maka itu menjadi C#. Nada tersebut merupakan peningkatan setengah langkah di atas nada C.
Tanda kres (#) juga dapat ditemukan dalam notasi musik untuk menunjukkan kunci atau akor yang menggunakan nada-nada yang ditingkatkan setengah langkah. Secara umum, tanda kres (#) digunakan dalam musik barat, sedangkan dalam musik lainnya seperti musik tradisional Timur, mungkin menggunakan simbol atau notasi yang berbeda untuk menunjukkan peningkatan tinggi sebuah nada. Sedangkan mol atau flat (b) adalah penandaan terhadap nada yang memiliki ½ nada lebih rendah. Sebagai contoh C#/Db yang berarti, nada C dinaikkan ½ nada atau nada D yang diturunkan ½ nada.
-
• Chord
Chord adalah kumpulan tiga atau lebih nada yang dimainkan secara bersamaan. Chord sering digunakan dalam musik untuk menciptakan harmoni dan memberikan dasar melodi. Dalam notasi musik, chord biasanya ditulis menggunakan huruf-huruf (A, B, C, dll.) yang mewakili nada-nada tertentu.
Chord terdiri dari beberapa elemen utama, yaitu:
-
1. Root Note (Nada Dasar): Nada dasar merupakan nada yang menjadi dasar atau acuan chord. Nada ini menentukan kualitas dan karakteristik dari chord tersebut. Misalnya, chord dengan nada dasar C akan dikenal sebagai chord C.
-
2. Interval: Interval adalah jarak antara nada-nada dalam chord. Interval ini menentukan jenis chord, apakah itu mayor, minor, augmented, diminished, dan sebagainya.
-
3. Kualitas Chord: Kualitas chord menunjukkan apakah chord tersebut mayor, minor, augmented, diminished, atau jenis kualitas lainnya. Hal ini ditentukan oleh jenis interval yang digunakan dalam chord.
Chord mayor terdiri dari tiga nada do, mi, sol, dan do sebagai root atau nada dasar. Sedangkan chord minor terdiri dari tiga nada do, ri, dan sol, dengan do juga sebagai root. Chord mayor biasa dituliskan CM atau C yang dibaca chord C mayor, sedangkan untuk chord minor dituliskan Cm yang dibaca chord C minor.
-
• Fast Fourier Transform (FFT)
Fast Fourier Transform (FFT) adalah suatu algoritma yang digunakan untuk melakukan perhitungan Transformasi Fourier secara efisien. Transformasi Fourier adalah teknik matematika yang digunakan untuk menganalisis sinyal dalam domain frekuensi. FFT merupakan implementasi cepat dari algoritma Transformasi Fourier Diskret (Discrete Fourier Transform - DFT) yang memungkinkan pengolahan sinyal secara lebih cepat.
Dalam konteks pemrosesan sinyal, FFT digunakan untuk mengubah sinyal dari domain waktu menjadi domain frekuensi. Dengan menerapkan FFT pada sinyal, kita dapat melihat komponen frekuensi yang terkandung di dalamnya. FFT memecah sinyal menjadi serangkaian nilai frekuensi yang membentuk spektrum frekuensi dari sinyal tersebut. Ini memungkinkan kita untuk menganalisis karakteristik frekuensi sinyal, seperti amplitudo (kekuatan) dan frekuensi komponen sinyal. FFT memiliki berbagai aplikasi di berbagai bidang, termasuk pemrosesan audio, pengolahan gambar, kompresi data, pemrosesan sinyal digital, analisis spektral, dan banyak lagi. Algoritma FFT telah dioptimalkan untuk melakukan perhitungan yang efisien, sehingga memungkinkan pengolahan sinyal dalam skala besar dengan kecepatan yang lebih tinggi daripada menggunakan metode konvensional. DFT sendiri merupakan proses transformasi sinyal dari domain waktu ke domain frekuensi.
Misalkan “x0, …, x(N-1)” merupakan bilangan kompleks. DFT didefinisikan dengan rumus:
x(nT) = 1 n∑ x(k)e jkΩπt, n = 0,1,2, ... , N - 1
Menghitung deret ini diperlukan operasi aritmatika sebanyak O(N2). Sedangkan algoritma FFT hanya memerlukan operasi sebanyak O (N log N) untuk menghitung deret yang sama
-
• Perancangan Flowchart Algoritma
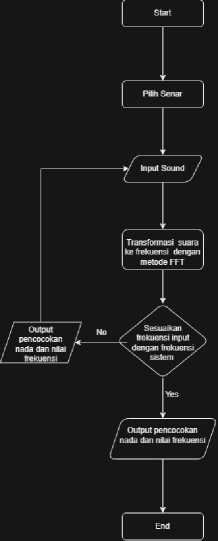
Gambar 1. Flowchart pada Citra Uji
-
• Diagram Konteks Sistem
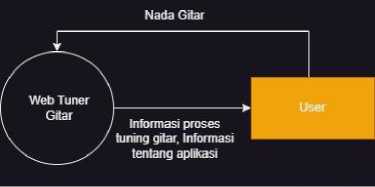
Gambar 2. Diagram Konteks Tuner Gitar
Pada penelitian ini dilakukan pengujian sistem dengan cara yaitu menggunakan gitar akustik bersenar enam dengan jarak 10 cm dan 20 cm berikut ini tabel pengujian sistem yang didapatkan
-
• Hasil Pengujian Penerapan Algoritma FFT dengan jarak 10 cm
Pengujian ini adalah pengujian black box terhadap algoritma FFT dengan menggunakan jarak 10 cm menggunakan gitar akustik (non elektrik).
Tabel 2. Frekuensi Uji FFT dengan jarak 10 cm dalam satuan Hz
Gitar Akustik Jarak 10 cm
|
No |
Frekuensi(Hz) | |||||
|
Senar 1 |
Senar 2 |
Senar 3 |
Senar 4 |
Senar 5 |
Senar 6 | |
|
1 |
658,800 |
496,196 |
390,527 |
294,083 |
219,947 |
165,139 |
|
2 |
658,604 |
495,563 |
390,743 |
294,146 |
219,457 |
165,069 |
|
3 |
658,546 |
496,280 |
391,816 |
294,726 |
220,385 |
164,686 |
|
4 |
658,221 |
495,359 |
391,480 |
294,498 |
219,686 |
164,751 |
|
5 |
658,445 |
495,672 |
390,938 |
293,519 |
219,082 |
164,818 |
|
6 |
658,417 |
495,274 |
391,845 |
293,607 |
219,600 |
165,054 |
|
7 |
659,554 |
496,021 |
391,090 |
294,611 |
219,325 |
165,239 |
|
8 |
657,793 |
495,954 |
391,834 |
293,929 |
219,189 |
165,011 |
|
9 |
658,567 |
495,079 |
390,963 |
294,295 |
219,276 |
164,363 |
|
10 |
658,296 |
496,086 |
391,692 |
294,737 |
219,699 |
164,989 |
|
Rata – Rata Frekuensi |
658,524 |
495,748 |
391,293 |
294,215 |
219,565 |
164,912 |
|
Standar Frekuensi |
659,260 |
493,880 |
392,000 |
293,660 |
220,000 |
164,81 |
|
Error |
0,734 |
1,868 |
0,707 |
0,555 |
0,435 |
0,102 |
Pada Tabel-2 terdapat R. Frekuensi, F. Standar dan Error. Rata - Rata Frekuensi adalah nilai rata-rata frekuensi yang didapatkan dari 10 percobaan, sedangkan Standar Frekuensi adalah frekuensi standar yang dimiliki oleh tiap senar. Error adalah nilai selisih antara F.standar dan R. Frekuensi. Pada Tabel-2 terlihat bahwa error terbesar adalah 1,868 yaitu pada senar dua sedangkan error terkecil pada senar enam sebesar 0,102. Dari error tersebut dapat kita hitung nilai rata-rata error adalah 0,7335. Hal ini berarti tingkat akurasi tuning gitar pada jarak 10 cm adalah 97%
-
• Hasil Pengujian Penerapan algoritma FFT dengan jarak 20 cm
Pengujian ini adalah pengujian black box terhadap algoritma FFT dengan menggunakan jarak 20 cm menggunakan gitar akustik (non elektrik).
Tabel 3. Frekuensi Uji FFT dengan jarak 20 cm dalam satuan Hz
Gitar Akustik Jarak 20 cm
|
No |
Frekuensi(Hz) | |||||
|
Senar 1 |
Senar 2 |
Senar 3 |
Senar 4 |
Senar 5 |
Senar 6 | |
|
1 |
658,800 |
493,196 |
391,529 |
294,083 |
219,947 |
165,139 |
|
2 |
658,729 |
495,563 |
391,743 |
293,145 |
219,457 |
165,069 |
|
3 |
658,451 |
495,280 |
391,816 |
294,726 |
220,385 |
164,686 |
|
4 |
658,110 |
494,359 |
391,480 |
293,498 |
219,686 |
164,751 |
|
5 |
658,803 |
494,672 |
390,938 |
295,519 |
219,082 |
164,818 |
|
6 |
658,417 |
494,274 |
391,845 |
293,607 |
219,600 |
164,154 |
|
7 |
659,069 |
495,021 |
391,090 |
294,611 |
220,308 |
164,239 |
|
8 |
657,793 |
494,954 |
391,834 |
293,929 |
219,727 |
164,211 |
|
9 |
658,567 |
495,079 |
390,963 |
294,420 |
220,276 |
164,363 |
|
10 |
658,603 |
494,086 |
391,692 |
293,737 |
219,012 |
164,989 |
|
Rata – Rata Frekuensi |
658,534 |
494,648 |
391,493 |
294,128 |
219,748 |
164,642 |
|
Standar Frekuensi |
659,260 |
493,880 |
392,000 |
293,660 |
220,000 |
164,81 |
|
Error |
0,726 |
0,768 |
0,507 |
0,468 |
0,252 |
0,168 |
Pada Tabel-3 terdapat R. Frekuensi, F. Standar dan Error. Rata - Rata Frekuensi adalah nilai rata-rata frekuensi yang didapatkan dari 10 percobaan, sedangkan Standar Frekuensi adalah frekuensi standar yang dimiliki oleh tiap senar. Error adalah nilai selisih antara F.standar dan R. Frekuensi. Pada Tabel-3 terlihat bahwa error terbesar adalah 0,768 yaitu pada senar dua sedangkan error terkecil pada senar enam sebesar 0,168. Dari error
tersebut dapat kita hitung nilai rata-rata error adalah 0,4815. Hal ini berarti tingkat akurasi tuning gitar pada jarak 10 cm adalah 99%
Tabel 4. Perbandingan Uji FFT dengan Jarak 10 dan 20 cm
Gitar Akustik (Non Elektrik) Jarak 20 cm
Frekuensi (Hz)
|
Senar 1 |
Senar 2 |
Senar 3 |
Senar 4 |
Senar 5 |
Senar 6 | |
|
Rata – Rata Error |
658,534 |
494,648 |
391,493 |
294,128 |
219,748 |
164,642 |
|
Standar Frekuensi |
659,260 |
493,880 |
392,000 |
293,660 |
220,000 |
164,81 |
|
Error |
0,726 |
0,768 |
0,507 |
0,468 |
0,252 |
0,168 |
|
Rata – Rata Error |
0,4815 | |||||
|
Gitar Akustik (Non Elektrik) Jarak 10 cm | ||||||
|
Frekuensi (Hz) | ||||||
|
Senar 1 |
Senar 2 |
Senar 3 |
Senar 4 |
Senar 5 |
Senar 6 | |
|
Rata – Rata Error |
658,524 |
495,748 |
391,293 |
294,215 |
219,565 |
164,912 |
|
Standar Frekuensi |
659,260 |
493,880 |
392,000 |
293,660 |
220,000 |
164,81 |
|
Error |
0,734 |
1,868 |
0,707 |
0,555 |
0,435 |
0,102 |
|
Rata – Rata Error |
0,7335 | |||||
Dari Tabel-4, jarak terbaik untuk melakukan tuning gitar dengan web ini adalah 20 cm. Ini dipengaruhi oleh kuat intensitas suara senar gitar, karena pada jarak yang terlalu jauh suara akan sulit ditangkap oleh mikrofon. Begitu juga jika jarak terlalu dekat, Suara yang dihasilkan senar akan menghasilkan noise.
Berdasarkan analisa perancangan sistem, implementasi dan pengujian sistem, maka dapat disimpulkan bahwa:
-
1. Algoritma Fast Fourier Transform yang diimplementasikan pada aplikasi ini memberikan hasil yang optimal untuk tuning gitar non elektrik. Berdasarkan pengujian tingkat akurasi tuning gitar mencapai 99%.
-
2. Jarak terbaik untuk melakukan tuning adalah 20 cm dengan error mencapai 0,4815. Hal ini dipengaruhi oleh kuat intensitas suara senar gitar, karena pada jarak yang terlalu jauh suara akan sulit ditangkap oleh mikrofon. Begitu juga jika jarak terlalu dekat maka suara yang dihasilkan oleh senar akan menghasilkan noise.
-
3. Web ini berhasil mengimplementasikan algoritma Fast Fourier Transform dalam melakukan tuning guitar.
Daftar Pustaka
-
[1] TEKNIKA, Volume 10(3), November 2021, pp. 189-198 ISSN 2549-8037, EISSN 25498045
-
[2] Yulio, I.B., Wijayanto, I. & Susatio, E. (2016). Perancangan dan Implementasi Tuner Gitar Berbasis Fast Fourier Transform dan Harmonic Product Spectrum Pada Platform Android. e-Proceeding of Engineering, Vol.3(2), pp. 1536-1543.
-
[3] Selamat, Tanda dan Kevin Angkasa. 2013. “Perangkat Lunak Tuning Gitar dengan Menggunakan Karplus Strong Algorithm”. Program Sarjana. Universitas STMIK IBBI Medan.
-
[4] Liu, W., Liao Q., Qiao, F., Xia, W., Wang. C. & Lombardi. F. (2017). Approximate Designs for Fast fourier transform (FFT) With Application to Speech Recognition. IEEE Transactions on Circuits and System 1: Regular Papers, Vol. 66(12), pp. 4727-4739
-
[5] Oktarian, N., Sharippudin & Irawan. (2020). Perancangan Aplikasi Pembelajaran Musik GItar Berbasis Android. Jurnal Ilmiah Mahasiswa Teknik Informatika, Vol. 2(3), pp. 186198.
-
[6] Wiflihani. 2013. “Pengetahuan Dasar Teori Musik”. Universitas Negeri Medan.
304
Discussion and feedback