Uji Performansi Algoritma Linear Regression dan Random Forest Regression pada Implementasi Sistem Prediksi Harga Rumah
on
JNATIA Volume 1, Nomor 3, Mei 2023
Jurnal Nasional Teknologi Informasi dan Aplikasinya
p-ISSN: 2986-3929
Uji Performansi Algoritma LR dan RFR pada Implementasi Sistem Prediksi Harga Rumah
I Putu Teddy Dharma Wijayaa1, Ida Bagus Dwidasmaraa2
aProgram Studi Informatika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana
Jalan Raya Kampus Udayana, Bukit Jimbaran, Kuta Selatan, Badung, Bali Indonesia
1 dharmawijaya077@student.unud.ac.id
-
2 dwidasmara@unud.ac.id (Corresponding Author)
Abstract
Currently the house has become one of the needs that must be met. The price of a house is the main parameter that determines whether a person or organization buys or invests. In general, house prices are influenced by several factors, including building area, land area, number of bedrooms, number of bathrooms and number of garages. Currently, there are many websites devoted to providing information about buying and selling houses. This of course makes it easier for someone when looking for a house with the desired specifications without the need to come directly to the location. However, the house buying and selling platform does not provide a house price prediction feature that is in accordance with user specifications. This means someone who is planning to buy a house does not get an initial idea of the costs that must be spent to own the desired home. Therefore, in this study, researchers will design a web app-based house price prediction system that can make it easier for users to get predictions of the desired house price. In this study the prediction algorithms to be used are linear regression and random forest. Both algorithms will be analyzed for their performance and then the algorithm with the best level of accuracy will be applied as a predictive model which will be integrated with the user interface display.
Keywords: Harga Rumah, Linear Regression, Random Forest Regression
Secara umum, rumah merupakan bangunan yang digunakan sebagai tempat tinggal dalam jangka waktu tertentu. Saat ini, rumah sudah menjadi kebutuhan primer bahkan sudah dijadikan alat untuk berinvestasi di masa yang akan datang dikarenakan harga yang cenderung berubah tiap waktunya serta banyaknya proses transaksi jual beli. Seiring berjalannya waktu, kebutuhan fisiologis manusia akan semakin bertambah salah satunya adalah kebutuhan dalam membeli rumah. Pengusaha properti akan berlomba-lomba membeli lahan perumahan yang kemudian akan dijual kembali kepada pembeli. Hal inilah yang menjadi salah satu faktor kuat yang menyebabkan harga rumah cenderung naik setiap tahunnya. Namun hal ini juga yang akan membuat masyarakat ragu dalam membeli rumah yang diinginkan. Harga yang terus berubah dan tidak bisa diprediksi membuat investor atau pembeli rumah memerlukan sebuah sistem yang dapat melakukan prediksi harga rumah berdasarkan beberapa parameter. Saat ini, salah satu metode machine learning yaitu prediksi sudah banyak digunakan sebagai bahan pertimbangan dalam pengambilan keputusan pembelian [1]. Hingga kini sudah banyak jurnal penelitian yang membahas prediksi harga rumah diantaranya, penelitian dengan judul “Analisis Prediksi Harga Rumah Sesuai Spesifikasi Menggunakan Multiple Linear Regression” yang dilakukan oleh M.Mu’tashm diperoleh hasil akurasi dari Multiple Linear Regression dalam prediksi harga rumah sebesar 66% [2]. Penelitian serupa yang dilakukan oleh Sefto P. (2016) dengan judul penelitian “Prediksi Harga Tanah menggunakan Algoritma Linear Regression” memberikan hasil akurasi yang tinggi dan RMSE terendah dengan data training 70% dan sisanya digunakan sebagai data testing yaitu sebesar 30% [3]. Berdasarkan penelitian yang sudah dilakukan sebelumnya dengan topik yang sama, algoritma Linear Regression merupakan algoritma yang paling banyak digunakan dalam penelitian topik prediksi harga rumah. Pada penelitian ini, selain algoritma
Linear Regression yang digunakan untuk prediksi harga rumah, penulis juga akan menggunakan algoritma Random Forest Regression sebagai pembanding dari algoritma Linear Regression. Random Forest Regression merupakan algoritma terawasi yang menggunakan metode pembelajaran ensemble untuk regresi sebagai teknik dengan melakukan penggabungan prediksi dari beberapa prosedur pemecahan dalam machine learning untuk menghasilkan hasil yang akurat pada model tunggal yang dirancang [4][5]. Terdapat beberapa penelitian mengenai penerapan dari algoritma Random Forest dalam kasus prediksi, misalnya pada penelitian yang dilakukan oleh Agri P., dkk (2019) dengan judul “Prediksi Pergerakan Harga Saham dengan Metode Random Forest Menggunakan Trend Deterministic Data Preparation”. Dari penelitian tersebut dihasilkan bahwa akurasi model yang dibangun dengan algoritma Random Forest pada data Trend deterministic adalah sebesar 61,40% dan pada data non-Trend deterministic adalah sebesar 75,76% [6]. Penelitian yang dilakukan oleh Egas S. dan Ida A. (2022) dengan judul ‘Penerapan Random Forest Regression Untuk Memprediksi Harga Jual Rumah Dan Cosine Similarity Untuk Rekomendasi Rumah Pada Provinsi Jawa Barat:” Dari penelitian tersebut diperoleh hasil precision sebesar 78%, recall 100% dan akurasi sebesar 80%. Pada penelitian kali ini, penulis akan melakukan komparasi performa algoritma Linear Regression dengan Random Forest Regression. Komparasi performa meliputi MSE (Mean Squared Root), MAE (Mean Absolute Error) dan R2 Score dari kedua model tersebut. Penulis juga akan melakukan optimalisasi kinerja dari kedua algoritma tersebut dengan metode grid search serta mencari kombinasi yang terbaik dari pembagian data train dan data test. Algoritma yang memiliki performa terbaik akan digunakan sebagai bagian dari model yang akan diintegrasikan dengan user interface pada sistem prediksi.
Gambar 1. Tahapan Penelitian
Pada Gambar 1, dapat dilihat tahapan dari penelitian yang akan dibuat. Terdapat tujuh proses dalam penelitian ini. Pada tahap pertama proses dimulai dari pengumpulan dataset, pemilihan algoritma yaitu Linear Regression dan Random Forest, analisis hasil prediksi, uji akurasi,
optimalisasi dengan metode grid search, uji akurasi final kemudian integrasi model dengan user interface:
-
2.1 Pengumpulan Data
Pengumpulan dataset dilakukan dengan mengunduh dataset harga rumah yang didapatkan dari platform Kaagle pada laman “https://www.kaggle.com/datasets/gustiosamba/datarumahjaksel”. Berdasarkan data yang didapatkan, dapat dilihat bahwa dataset terdiri dari 4 kolom yaitu harga rumah, luas bangunan, luas tanah, jumlah kamar mandi, jumlah kamar tidur dan jumlah garasi dengan total baris sebanyak 1010. Kolom luas bangunan, luas tanah, jumlah kamar mandi, jumlah kamar tidur dan jumlah garasi akan dijadikan features sedangkan kolom harga akan menjadi target features. Pada proses train, jumlah data yang digunakan akan divariasikan sebanyak 70%, 80% dan 90%. Hal ini dilakukan dengan tujuan untuk mengetahui jumlah data train optimal yang dapat digunakan.
-
2.2 Pemilihan Algoritma
Algoritma yang akan digunakan pada penelitian ini adalah Random Forest Regressoin dan Linear Regression. Kedua algoritma ini kemudian akan dibandingkan akurasi yang dihasilkan dengan metode MSE (Mean Squared Root), MAE (Mean Absolute Error) dan R2 Score
-
a. Linear Regression
Linear regression merupakan metode statistik yang digunakan untuk mengetahui pengaruh beberapa variabel terhadap satu buah variabel yang menjadi target [7]. Secara matematis Linear Regression akan mencari hubungan variabel dependen (y) dengan variabel independen (x) [8]. Berikut merupakan persamaan matematis dari metode Linear Regression [9]:
y = a + wx (1)
a = y — wχ
(2)
(3)
w - ∑nxi (yi-y)
w
∑∙1xi (xi-x)
Dengan w merupakan vektor bobot sedangkan a adalah intercept yang merupakan sebuah nilai skalar yang di dalam bidang machine learning disebut dengan istilah bias. Sehingga, secara umum model linear regression dapat diartikan sebagai penggunaan suatu fungsi lurus atau datar. Jadi pembelajaran (learning) pada model linear adalah untuk menentukan dua parameter yaitu a dan w.
-
b. Random Forest Regression
Random Forest Regression merupakan kombinasi pohon keputusan sedemikian sehingga setiap pohon akan bergantung pada nilai nilai dari vektor acak yang disamping secara independen dan dengan distribusi yang sama untuk semua pohon dalam hutan tersebut. Keunggulan dari Random Forest Regression dibandingkan dengan Linear Regression adalah pada seleksi acak untuk memilih setiap simpul (node) yang mampu menghasilkan tingkat kesalahan yang rendah. Proses pelatihan dari Random Forest Regression melibatkan pembangunan banyak pohon keputusan secara paralel dan independen. Ketika melakukan prediksi, setiap pohon akan memberikan prediksi berdasarkan fitur yang ada serta hasil prediksi setiap pohon yang sudah dibangun. Random Forest Regression dapat bekerja optimal pada data yang tidak seimbang dan memiliki kemampuan untuk mengevaluasi kepentingan fitur dalam prediksi. Dalam algoritma Random Forest Regression parameter jumlah pohon (n_estimators), kedalaman pohon (max_depth) serta jumlah fitur yang digunakan dalam setiap pohon (max_features) akan mempengaruhi kinerja dari algoritma Random Forest Regression.
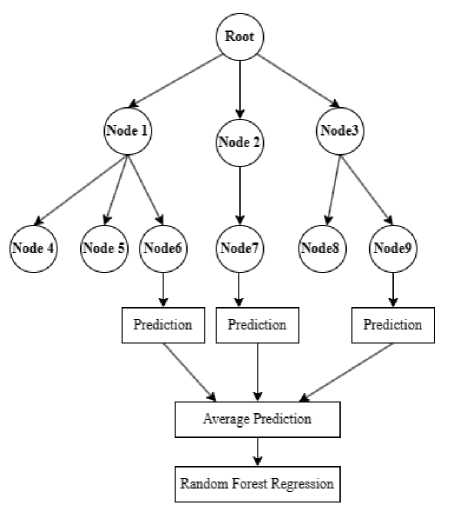
Gambar 2. Cara kerja dari algoritma Random Forest Regression
-
2.3 Uji Akurasi
Salah satu tahapan dalam proses penelitian yang sudah dijelaskan pada gambar 1 adalah uji akurasi. Pada penelitian ini, penulis akan melakukan uji akurasi sebanyak dua kali yaitu uji akurasi model tanpa optimalisasi Grid Search serta dengan optimalisasi Grid Search. Pada tahap uji akurasi, metode yang akan digunakan adalah sebagai berikut
-
a. MSE (Mean Squared Root)
MSE merupakan rata rata kuadrat kesalahan yang dihitung dengan menjumlahkan semua kesalahan atau eror prediksi yang dihasilkan oleh suatu model kemudian dikuadratkan dan membaginya dengan jumlah periode prediksi [10]. Berikut merupakan persamaan matematis dari MSE:
MSE = 1 ∑in(Xi - Fi)2 (4)
Keterangan:
Xi = Data aktual pada periode ke-i
Fi = Nilai hasil prediksi atau prediksi pada period ke-i
-
n = Banyaknya sampel
-
b. MAE (Mean Absolute Error)
MAE merupakan selisih absolut antara nilai prediksi dan nilai yang sebenarnya kemudian akan dihitung rata rata dari selisih tersebut. MAE dapat memberikan gambaeran rata rata prediksi dengan nilai yang sebenarnya. Berikut merupakan persamaan matematis dari MAE:
MAE = 1 ∑in |yi - ŷ (5)
Keterangan:
n = Banyaknya sampel
yi = nilai aktual pada sampel ke i
ŷ = nilai prediksi pada sampel ke i
-
c. R2 Score
R2 Score digunakan untuk mengukur sejauh mana variabilitas suatu model statistic atau machine learning dapat menjelaskan variasi data yang diamati. Range nilai dari R2 Score adalah antara 0 hingga 1. Berikut merupakan persamaan matematis dari R2 Score:
2 ∑in=1 (yi- ŷi)2
(6)
R = 1 - ∑in=1(yi- y̅i)2
Keterangan:
yi = Nilai aktual dari variabel dependen
ŷi = Nilai aktual dari variabel dependen
̅y = Nilai rata rata dari variabel dependen
Pada penelitian ini, jumlah total data yang digunakan adalah sebanyak 1010 baris dengan 9 buah kolom yang meliputi No, Nama Rumah, Harga, Luas Bangunan (LB), Luas Tanah (LT), Kamar Mandi (KM), Kamar Tidur (KT), Garasi (GRS). Dataset yang digunakan merupakan dataset harga rumah yang terdapat pada daerah Jakarta Selatan. Informasi lebih jelas dari dataset yang digunakan dapat diakses pada https://www.kaggle.com/datasets/gustiosamba/datarumahjaksel.
|
NO |
NAMA RUMAH |
HARGA |
LB |
LT |
KT |
KM |
GRS | |
|
O |
1 |
Rumah Murah Hook Tebet Timur, Tebet1 Jakarta S... |
3800000000 |
220 |
220 |
3 |
3 |
0 |
|
1 |
2 |
Rumah Modern di Tebet dekat Stasiun, Tebet, Ja... |
4600000000 |
180 |
137 |
4 |
3 |
2 |
|
2 |
3 |
Rumah Mewah 2 Lantai Hanya 3 Menit Ke Tebet, T... |
3000000000 |
267 |
250 |
4 |
4 |
4 |
|
3 |
4 |
Rumah Baru Tebet, Tebet, Jakarta Selatan |
430000000 |
40 |
25 |
2 |
2 |
0 |
|
4 |
5 |
Rumah Bagus Tebet komp Gudang Peluru It 350m,... |
9000000000 |
400 |
355 |
6 |
5 |
3 |
Gambar 3. Dataset yang Digunakan Dalam Perancangan Model
Data yang sudah dipersiapkan kemudian akan dibagi menjadi data latih dan juga data uji. Pada penelitian ini data latih akan divariasikan jumlahnya yaitu sebanyak 70%, 80% dan 90%. Hasil yang didapatkan dari algoritma Random Forest Regression adalah sebagai berikut
Tabel 1. Performa Algoritma Random Forest Regression
|
Jumlah Dataset |
MSE |
MAE |
R2 SCORE |
|
70% |
24119623.92 |
1979.89 |
0.683 |
|
80% |
24262964.70 |
1825.28 |
0.667 |
|
90% |
1184164.61 |
1708.59 |
0.83 |
Dengan konfigurasi yang sama pada algoritma Linear Regression maka diperoleh hasil sebagai berikut:
Tabel 2. Performa Algoritma Linear Regression
|
Jumlah Dataset |
MSE |
MAE |
R2 SCORE |
|
70% |
23723834.90 |
2102.96 |
0.69 |
|
80% |
26499374.32 |
2103.67 |
0.64 |
|
90% |
14911490.56 |
2091.32 |
0.75 |
Untuk mendapatkan performa terbaik dari kedua algoritma tersebut, maka langkah selanjutnya adalah melakukan optimalisasi menggunakan metode Grid Search. Berikut merupakan konfigurasi pada Grid Search pada kedua model:
Tabel 3. Parameter yang Digunakan pada Grid Search
|
Algoritma |
Parameter 1 |
Parameter 2 |
Parameter 3 |
Parameter 4 |
|
Random Forest Regression |
n_estimators = [100, 200, 300] |
max_depth = [5, 10, 15] |
min_samples_split = [2,5,10] |
min_samples_leaf = [1,2,3,4] |
|
Linear Regression |
positive = [True, False] |
fit_intercept = [True, False] |
copy_X = [True, False] |
- |
Tabel 4. Nilai parameter hasil optimisasi Grid Search pada Algoritma Random Forest Regression
|
Jumlah Dataset Max_depth |
Min_samples_leaf |
Min_sample_leaf N_estimators | ||
|
70% |
15 |
3 |
2 |
300 |
|
80% |
20 |
2 |
2 |
200 |
|
90% |
20 |
3 |
5 |
300 |
Tabel 5. Performa Algoritma Random Forest Regression hasil optimisasi Grid Search
Jumlah Dataset MSE MAE R2 SCORE
Tabel 6. Nilai Parameter hasil Optimisasi Grid Search pada Algoritma Linear Regression
Jumlah Dataset Positive Fit_intercept Copy_X
70% False False True
80% False True True
90% False False True
Tabel 7. Performa Algoritma Linear Regression Hasil Optimisasi Grid Search
Jumlah Dataset MSE MAE R2 SCORE
70% 15039552.95 2143.05 0.75
Jumlah Dataset MSE MAE R2 SCORE
80% 26499374.32 2103.67 0.63
90% 15039552.95 2143.05 0.75
Berdasarkan hasil percobaaan, baik sebelum dan sesudah dilakukan optimisasi dengan metode grid search diperoleh hasil bahwa Random Forest Regression memiliki rata rata performa yang lebih baik dibandingkan dengan Linear Regression terutama pada data latih diatas dari 70%. Ketika data training dibuat menjadi sebanyak 70% dan dengan teknik optimisasi grid search, algoritma Linear Regression menunjukkan performa yang jauh lebih baik dibandingkan dengan algoritma Random Forest Regression terutama pada nilai MSE dan R2 Score. Hal ini membuktikan bahwa meskipun algoritma Random Forest Regression membentuk n estimators pohon namun tidak menjamin memiliki performa yang selalu lebih baik dibandingkan dengan algoritma Linear Regression. Berdasarkan data tabel 5, model terbaik yang diperoleh adalah model yang menggunakan Algoritma Random Forest Regression dengan jumlah dataset sebanyak 90%, dan dengan parameter yang sesuai pada tabel 4.
-
3.2 Integrasi Model dengan User Interface
Pada penelitian ini, peneliti menggunakan library streamlit yang digunakan dalam pembuatan antaramuka sistem sehingga dapat mempermudah pengguna dalam melakukan prediksi harga rumah. Library streamlit dipilih karena penggunaannya yang mudah sehingga mempercepat proses deployment sistem yang dirancang. Dalam proses integrasi antara model dengan User Interface diperlukan sebuah tes yang dinamakan dengan integration testing. Berikut merupakan integration testing yang sudah dilakukan pada sistem prediksi harga rumah yang sudah dirancang.
Tabel 8. …
No Integration Testing Status
-
1. Pengujian pada text input Succced
-
2. Pengujian tombol tambah pada number input Succced
-
3. Pengujian pada tombol submit Succced
-
4. Sistem menampilkan hasil prediksi berdasarkan model Succced
SISTEM INFORMASI PREDIKSI HARGA RUMAH
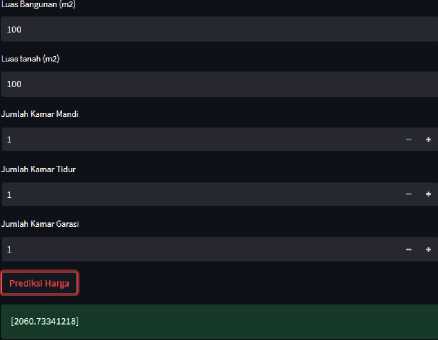
Gambar 4. Tampilan Antarmuka Sistem yang Dirancang
Berdasarkan percobaan yang dilakukan pada algoritma Linear Regression dengan Random Forest Regression diperoleh hasil akhir bahwa algoritma Random Forest Regression memiliki performa yang lebih baik dibandingkan dengan algoritma Linear Regression. Terutama pada persentase jumlah data train sebanyak 90% dan sudah dilakukan optimisasi dengan teknik Grid Search. Dimana pada persentase jumlah data train tersebut Algoritma Random Forest lebih baik hampir 10% jika dibandingkan dengan algoritma Linear Regression. Hal ini disebabkan pada algoritma Random Forest menggunakan lebih dari satu model pohon (n_estimators) yang kemudian dicari nilai tengah atau rata rata dari masing masing model pohon yang sudah dibangun. Namun pada persentase data train 70% dan 80% baik Random Forest Regression maupun Linear Regression tidak menunjukkan perbedaan yang signifikan. Oleh karenanya jumlah dari data train berperan penting dalam perancangan model ini.
Daftar Pustaka
-
[1] G. N. A. d. D. Fitrianah, "Penerapan Metode Regresi Linear Untuk Prediksi Penjualan
Properti pada PT XYZ," J. Telemat, vol. 14, p. 79–86, 2019.
-
[2] F. N. R. F. N. R. Evi Febrion Rahayuningtyas, "Prediksi Harga Rumah Menggunakan
General Regression Neural Network," JURNAL INFORMATIKA, vol. 8, pp. 59-66, 2021.
-
[3] S. Pratama, "PREDIKSI HARGA TANAH MENGGUNAKAN ALGORITMA LINEAR REGRESSION," Technologia, vol. 7, 2016.
-
[4] T. P. J. A. Yani, "Sistem Klasifikasi Variabel Tingkat Penerimaan Konsumen Terhadap Mobil Menggunakan Metode Random Forest," J. Tek. Elektro, vol. 9, p. 24–29, 2017.
-
[5] "S. Dutalia, A. K. Lalo, P. Batarius, Y. Carmeneja, H. Siki," Implementasi Algoritma C4 . 5
Untuk Klasifikasi Penjualan, vol. 06, p. 1–12, 2021.
-
[6] F. R. Setiawan, "Prediksi Pergerakan Harga Saham dengan Metode Support Vector Machine (SVM) Menggunakan Trend Deterministic Data Preparation( Studi Kasus Saham Perusahaan PT Astra International Tbk, PT Garuda Indonesia Tbk, dan PT Indosat Tbk )," e-Proceeding of Engineering, vol. 5, p. 8356, 2018.
-
[7] T. W. P. I. Heru Wahyu, "Penerapan Algoritme Linear Regression untuk Prediksi Hasil Panen Tanaman Padi," Jurnal Nasional Teknik Elektro dan Teknologi Informasi (JNTETI), vol. 4, p. 364, 2019.
-
[8] I. K. G. S. Indra Permana Putra, "Perbandingan Akurasi Algoritma Regresi Linier, Regresi Polinomial, dan Support Vector Regression Pada Model Sistem Prediksi Harga Rumah," JNATIA, vol. 1, 2022.
-
[9] T. K. a. R. Nindyasari, "Forecasting Dengan Metode Regresi Linier Pada Sistem Penunjang Keputusan Untuk Memprediksi Jumlah Penjualan Batik (Studi Kasus Kub Sarwo Endah Batik Tulis Lasem)," J. Mantik Penusa, vol. 1, p. 71–92, 2017.
-
[10] S. H. F. R. T. V. Heri Setyawan, "Prediksi Tingkat Produksi Buah Kelapa Sawit dengan Metode Single Moving Average," J.TIKomSiN, vol. 9, pp. 1-10, 2021.
924

Discussion and feedback