Implementasi Algoritma A* (Star) dengan Graf untuk Menentukan Rute Terpendek Distributor Kopi
on
JNATIA Volume 1, Nomor 4, Agustus 2023
Jurnal Nasional Teknologi Informasi dan Aplikasinya
p-ISSN: 2986-3929
Implementasi Algoritma A* (Star) dengan Graf untuk Menentukan Rute Terpendek Distributor Kopi
I Putu Andi Wiratama Putraa1, I Gede Arta Wibawaa2
aProgram Studi Informatika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Udayana
Jalan Raya Kampus Udayana, Bukit Jimbaran, Kuta Selatan, Badung, Bali Indonesia 1andiwp2003@gmail.com 2gedearta83@gmail.com
Abstract
In this research, the A Star algorithm is employed to find the most efficient route for goods distribution. Distributors encounter challenges in ensuring timely deliveries due to the presence of multiple destinations spread across different regions. Congestion further adds to the complexity of determining the shortest path. The A Star algorithm utilizes the distance-plus-cost function to prioritize the order of visiting points. This study utilizes primary data, comprising five shop locations in the Tabanan city, as nodes and incorporates the distances between the shops. The implemented program utilizes the A Star algorithm to compute the shortest route and present the path along with its corresponding distance. The objective of this research is to attain the shortest route and calculate the distance covered for the coffee distributor.
Keywords: A Star, Shortest Route, Graph
Dalam kehidupan sehari-hari, ketika berpindah dari satu tempat ke tempat lain, yang menjadi perhatian utama adalah efisiensi waktu dan biaya. Untuk itu, kita memerlukan informasi untuk menentukan rute terpendek antar tempat yang ingin kita jangkau. Algoritma yang digunakan untuk mencari jalur terpendek disebut juga sebagai algoritma jalur terpendek, digunakan untuk menentukan jalur dalam suatu graf [1]. Graf adalah gabungan dari simpul (vertices) dan edge (tepi), dimana setiap edge dihubungkan dengan satu atau dua simpul. Penerapan graf dan keterhubungannya dalam kehidupan nyata sering kita jumpai dalam berbagai bidang seperti komunikasi informasi, jaringan komputer, lalu lintas, jaringan listrik dan saluran air [2]. Distributor adalah badan usaha yang bertanggung jawab untuk mendistribusikan produk dari satu lokasi ke lokasi lain. Peran distributor sangat penting untuk menjamin ketersediaan dan pendistribusian produk yang dibutuhkan masyarakat. Sebagai perantara dalam proses pemasaran, distributor bertanggung jawab atas pengangkutan dan penyimpanan barang dan jasa dari produsen ke konsumen. Dalam peran pemasaran, distributor harus melakukan perjalanan untuk mengirimkan barang ke lokasi yang berbeda. Namun, distributor sering menghadapi tantangan dalam proses pengiriman, seperti waktu tempuh yang lama dan kesulitan dalam mengurutkan kunjungan secara efisien. Faktor tersebut seringkali dikarenakan luasnya wilayah yang harus mereka layani dan seringnya masalah kemacetan saat perjalanan. Algoritma A Star adalah metode yang diperkaya dengan penggunaan heuristik. Algoritma ini menghilangkan langkah-langkah pucat karena langkah-langkah ini tidak mengarah pada solusi yang diinginkan. Algoritma A Star yang digunakan untuk mencari rute terdekat mencakup perhitungan heuristik. Setelah nilai heuristik didapatkan, langkah selanjutnya adalah mencari nilai f(n). Nilai F(n) kemudian dimasukkan ke dalam open list. Kemudian bobot antar node diperhitungkan dan node dengan bobot terendah dipilih sebagai jalur [3]. Algoritme A Star menghitung dan menyimpan semua kemungkinan untuk membandingkan setiap jalur yang dipilih dengan jalur tersimpan lainnya. Hal ini mengarah pada solusi optimal dalam pencarian jarak terpendek. Tujuan utama dari penelitian ini adalah untuk menemukan saluran distribusi barang yang optimal dengan menggunakan algoritma A Star. Penelitian ini berfokus pada pendistribusian barang di jalan khususnya pada beberapa toko yang berada di Kabupaten Tabanan. Pada penelitian ini terdapat 5 toko yang melalui titik saluran distribusi. Pencarian rute terpendek diawali dengan informasi titik awal dan tujuan perjalanan distributor. Lokasi awal dan tujuan yang diberikan digunakan untuk menemukan rute terpendek.
Data yang digunakan dalam penelitian ini adalah data primer. Data tersebut mencakup informasi 5 toko yang teridentifikasi di wilayah perkotaan Tabanan. Setiap toko direpresentasikan pada grafik sebagai titik dengan lokasi sebagai simpul dan jarak antara toko sebagai tepi yang menghubungkannya. Jarak antar toko yang dimasukkan ke dalam sistem dan jumlah node bervariasi tergantung tujuan pengiriman yang ditentukan. Evaluasi hasil rute didasarkan pada perhitungan jarak, tanpa memperhitungkan faktor kemacetan atau kondisi geografis rute. Penentuan posisi menggunakan Google Earth sebagai panduan dan menghitung jarak antar titik dengan melihat bujur dan lintang lokasi yang dipilih.
-
2.2. Graf
Menggunakan grafik untuk memvisualisasikan objek diskrit dan hubungan di antara mereka adalah konsep umum. Dalam representasi visual, setiap objek direpresentasikan sebagai titik pada grafik, sedangkan hubungan antar objek direpresentasikan sebagai garis yang menghubungkan titik-titik tersebut. Grafik dapat digunakan untuk merepresentasikan berbagai informasi, salah satunya adalah peta [5].
-
2.3. Tahapan Algoritma A Star
Algoritma A Star merupakan metode pencarian jalur terpendek yang menggunakan fungsi heuristik untuk menentukan urutan kunjungan node. Fungsi heuristik ini memberikan estimasi atau skor pada setiap node yang membantu algoritma A Star untuk mencapai solusi yang diinginkan [3]. Menemukan jarak terpendek pada peta, peta harus disajikan sebagai diagram. Setiap simpul grafik mewakili persimpangan atau lokasi khusus di peta, sedangkan tepi grafik mewakili jalur yang dilalui. Tepi grafik memiliki bobot yang mencerminkan panjang jarak antar simpul. Algoritma Star mengevaluasi setiap node dengan menghubungkan g(n), yang merupakan biaya untuk mencapai node tersebut, dan h(n), yang merupakan perkiraan biaya untuk mencapai tujuan node tersebut. Dalam notasi matematika, ini dapat dinyatakan sebagai:
Rumus:
Π∏) = g(∏) + h(n)
(1)
Keterangan:
-
a. Nilai f(n) adalah hasil penjumlahan g(n) dan h(n). Nilai f(n) ini merupakan estimasi awal dari jalur terpendek. Sebenarnya, f(n) adalah jalur terpendek yang sebenarnya, tetapi tidak sepenuhnya dieksplorasi sampai algoritma A* dipecahkan.
-
b. Nilai g(n) adalah jarak total yang ditempuh dari titik awal ke titik saat ini (titik tujuan). Itu mencerminkan rintangan atau jarak yang ditempuh.
-
c. Nilai h(n) adalah perkiraan jarak dari titik saat ini (yang dikunjungi) ke titik tujuan. Fungsi heuristik digunakan untuk memperkirakan berapa lama waktu yang dibutuhkan untuk mencapai tujuan.
Beberapa istilah dari algoritma A Star [4] dapat dijelaskan sebagai berikut:
-
a. "Titik awal" mengacu pada posisi awal dalam algoritme.
-
b. "Node" adalah titik yang mewakili target dan bisa berbentuk persegi, segitiga atau lingkaran.
-
c. "A" adalah simpul yang digunakan untuk menemukan jalur terpendek.
-
d. "Open List" adalah sekumpulan node yang dapat diakses dari titik asal atau node yang sedang dievaluasi.
-
e. "Closed List" adalah kumpulan node yang dipilih sebagai bagian dari jalur terpendek.
-
f. “Harga” (F) adalah nilai yang dihitung dengan menjumlahkan nilai G yang merupakan penjumlahan dari nilai simpul-simpul jalur terpendek dari titik asal ke simpul A, dan nilai H yaitu estimasi jarak dari node tersebut ke tujuan.
Prinsip dari algoritma ini adalah mencari jalur terpendek dari titik awal (starting point) ke node tujuan, dengan biaya minimum (F).
Langkah-langkah algoritma A Star [4] adalah sebagai berikut:
-
a. Langkah pertama dimulai dengan simpul A sebagai titik awal.
-
b. Selanjutnya, semua node yang bertetangga dengan A dan tidak memiliki atribut barrier ditambahkan ke open list.
-
c. Kami kemudian mencari simpul dengan nilai H terkecil di antara simpul dalam daftar terbuka.
-
d. Setelah itu, A dipindahkan ke node dengan nilai H terkecil. Simpul sebelum A disimpan sebagai induk A dan ditambahkan ke daftar tertutup. Jika ada node lain yang bertetangga dengan A (yang telah dipindahkan) tetapi belum masuk ke dalam open list, node tersebut dimasukkan ke dalam open list.
-
e. Selanjutnya nilai G yang ada dibandingkan dengan nilai G sebelumnya. Jika nilai G yang baru lebih kecil, A kembali ke posisi semula. Node yang diuji termasuk dalam daftar tertutup. Proses ini diulangi hingga kami menemukan solusi atau tidak ada lagi node dalam daftar terbuka.
Pada penelitian ini penentuan rute terpendek dilakukan dengan mencari lokasi pada peta menggunakan informasi koordinat geografis (lintang dan bujur). Implementasi algoritma A Star untuk menentukan rute terpendek menuju dealer perusahaan dilakukan dengan menggunakan bahasa pemrograman Python. Tabel 1 di bawah menunjukkan tujuan pengiriman barang-barang yang digunakan dalam penelitian ini.
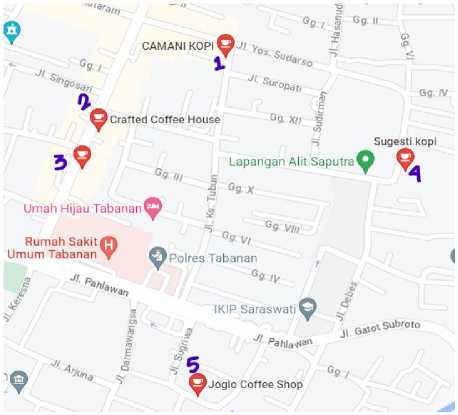
Gambar 1. Google Map Titik Awal dan Titik Tujuan
Tabel 1. Koordinat Latitude dan Longitude Titik Tujuan
|
No |
Titik Tujuan |
Latitude |
Longitude |
|
1 |
Camani Kopi |
-8.535638644370819 |
115.13396379698509 |
|
2 |
Crafted Coffee House |
-8.536900448812 |
115.13244771366291 |
|
3 |
Tan Panama |
-8.537571962922883 |
115.13177912233395 |
|
4 |
Sugesti Kopi |
-8.537561631945506 |
115.13683534425911 |
|
5 |
Joglo Coffee Shop |
-8.541133082729948 |
115.13367888799112 |
Berdasarkan titik koordinat bujur (Longitude) dan lintang (Latitude) yang didapatkan pada google maps, kemudian akan dilakukan perhitungan jarak antara satu titik ke titik lainnya dengan menggunakan persamaan berikut:
di∣ = (69 ∙ yJ(loni — Iontf + (lati — Iattf') ■ 1,60934 (2)
Dalam konteks ini:
-
a. "dij" mengacu pada jarak antara dua titik koordinat i dan j, diukur dalam kilometer.
-
b. "loni" merujuk pada nilai longitude dari titik i.
-
c. "lonj" merujuk pada nilai longitude dari titik j.
-
d. "lati" merujuk pada nilai latitude dari titik i.
-
e. "latj" merujuk pada nilai latitude dari titik j.
Keterangan:
Pada rumus diatas menggunakan rumus Haversine, dimana konstanta 69 yang digunakan bertujuan untuk mengonversi perbedaan dalam derajat lintang (latitude) menjadi jarak dalam mil. Ini didasarkan pada anggapan bahwa pada garis lintang rata-rata di Bumi, jarak sejajar satu derajat lintang sekitar 69 mil (atau 111,045 kilometer). Dengan menggunakan konstanta ini, kita dapat mengaproksimasi jarak dalam mil berdasarkan perbedaan lintang antara dua titik. Setelah kita menghitung jarak dalam mil menggunakan konstanta 69, kita perlu mengonversinya menjadi kilometer. Faktor 1,60934 digunakan untuk mengubah satuan jarak dari mil menjadi kilometer. Faktor ini adalah hasil dari konversi 1 mil menjadi kilometer (1 mil = 1,60934 kilometer). Dengan mengalikan jarak dalam mil dengan faktor ini, kita mendapatkan hasil jarak dalam kilometer.
Melakukan proses jarak masing-masing titik:
⅛ jarak,py > ...
-
1 from math import radians, sin, cos, sqrt, atan2
class Node:
def __init__(self, x, y): self.x = x self.y = y
-
8 # Menghitung jarak dari node nl dan n2 berdasarkan longitude dan Iatiti
def haversineDist(nl, n2):
R = 6371.0 # Radius bumi dalam kilometer
Iatl = radians(nl.x)
Icnl = radians(nl.y) lat2 = radians(n2.x) lon2 = radians(n2.y) dl□n = lon2 - Ionl dlat = lat2 - Iatl a = sin(dlat ∕ 2)**2 + cos(latl) * cos(lat2) * sin(dlon ∕ 2)**2 c - 2 “ atan2(sqrt(a), sqrt(l - a)) distance = R * c return round(distance, 4)
PROBLEMS OUTPUT DEBUG CONSOLE TERMINAL
C:∖Users∖putuandi∖OneDrive∖Documerτts∖Snatia∖code>python -u "c:∖Users∖putuandi∖(M Jarak antara nl dan nl: 3.0 km
Jarak antara nl dan n2: 3.2179 km
Jarak antara nl dan n3: 3.3224 km
Jarak antara nl dan ∏4: 3.3814 km
Jarak antara nl dan n5: 8.6118 km
Gambar 2. Mencari Jarak Antar Node
Berdasarkan perhitungan jarak antara titik/ tempat yang telah ditentukan sebelumnya. Hasil jarak tersebut akan direpresentasikan dalam satuan km dan dibulatkan 2 angka dibelakang koma sehingga diperoleh hasil sebagai berikut:
Tabel 2. Jarak Masing-Masing Titik Tujuan:
|
x |
1 |
2 |
3 |
4 |
5 |
|
1 |
0.00 |
0.22 |
0.32 |
0.38 |
0.61 |
|
2 |
0.22 |
0.00 |
0.11 |
0.49 |
0.44 |
|
3 |
0.32 |
0.11 |
0.00 |
0.56 |
0.45 |
|
4 |
0.38 |
0.49 |
0.56 |
0.00 |
0.53 |
|
5 |
0.61 |
0.44 |
0.45 |
0.53 |
0.00 |
Setelah mendapatkan jarak satu titik/ tempat ke titik/ tempat lainnya, maka selanjutkan kita dapt menghitung pencarian rute tercepat/ terbaik dengan mengimplementasikan algoritma A* di dalamnya.
import heapq
class Node:
def__Init__(self, name):
self.name = name
self.neighbors = {}
self.g_score = float(,inf,)
self.f_score = float(,inf,) self. camefrom = None
def add_neighbor(self, neighbor, weight):
self.neighbors[neighbor] = weight
def astar(start, goal):
open_set = []
heapq.heappush(open_set, (0, start))
start.g_score = O
start.f_score = heuristic(start, goal)
while open_set:
current = heapq.heappop(open_set)[l]
if current == goal:
return reconstruct_path(current)
for neighbor, weight in current.neighbors.items():
tentative_g_score = current.g_score + weight
if tentative_g_score < neighbor.g_score:
neighbor.camefrom = current
neighbor, gscore = Ientativegscore
neighbor.f score = tentative_g_score + heuristic(neighbor, goal) heapq.heappush{open_set, (neighbor.f_score, neighbor))
-
Gambar 3. Mencari Rute Terpendek Menggunakan Algoritma A*
Output program yang dikembangkan:
Masukkan titik awal: Cannani Kopi
Masukkan titik akhir: Ioglo Coffee Shop
Pengirinnan Biji Kopi dari Cannani Kopi ke Joglo Coffee Shop
Rute terpendek: Cannani Kopi -> Crafted Coffee House -> Tan Pananna -> Ioglo Coffee Shop Tarak tempuh: θ.75
-
Gambar 4. Output Yang Dihasilkan
Hasil program yang dijalankan di atas didapatkan berdasarkan proses pencarian rute menggunakan algoritma A* (Star), dimana pada program user dapat mengiputkan titik atau tempat yang akan dijadikan titik awal pengiriman kopi dan titik akhir pengiriman kopi berdasarkan tempat atau titik yang telah ditetapkan sebelumnya pada maps. Proses selanjutkan peneliti akan melakukan inputan agar dapat diimplementasikan oleh graf. Tujuan dari implementasi ini agar memudahkan dalam melihat tampilan arah peta pencarian rute yang lebih jelas dan detail.
Implementasi graf dalam menentukan rute terpendek:
import networkx as nx
import matplotlib.pyplot as pit
-
# Membangun graf graph = nx.Graph() graph.add_edge(''Camani Kopi", "Crafted Coffee House", weight=».22) graph.add_edge(''Camani Kopi", "Sugesti Kopi", weight=».38) graph.add edge(''Crafted Coffee House", "Tan Panama", weight=».11) graph.add_edge("Tan Panama", "Joglo Coffee Shop”, weight=».42) graph.add_edge("Sugesti Kopi", ''Joglo Coffee Shop”, weight=».53) graph.add_edge(”Joglo Coffee Shop", ''Sugesti Kopi'', weight=».45) graph.add edge(''Sugesti Kopi", ''Camani Kopi", weight=».38) graph.add_edge(”Joglo Coffee Shop", "Sugesti Kopi", weight=».53) graph.add_edge(''Tan Panama", "Crafted Coffee House", weight=».11)
-
# Menampilkan graf
pos = nx,Spring-Iayout(graph)
nx.draw(graph, pos, With labels=True, nodesize=500, font_size=12) edge labels = nx.getedgeattributes(graph, 'weight')
nx.draw networkx edge Iabelsfgraph, pos, edge labels=edge labels)
Gambar 5. Pencarian Rute Dengan Tampilan Graf
Output program yang dikembangkan:
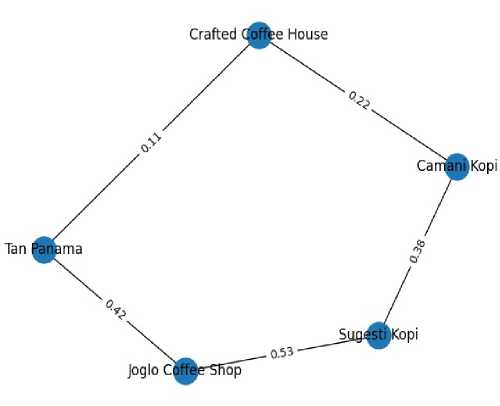
Gambar 6. Output Tampilan Graf
Pada pengujian ini, dilakukan variasi pada titik asal dan tujuan untuk mengevaluasi hasil algoritma A Star. Tujuan mengimplementasikan dalam bentuk graf, agar user dapat melihat tampilan dengan lebih jelas dan pasti terkait jarak antar titik/ tempat pendistribusian kopi. Hasil pengujian lengkap dari masing-masing titik atau tempat ke tempat tujuan dilihat pada tabel berikut:
Tabel 4. Hasil Pengujian Sistem
|
No |
Titik Awal |
Titik Tujuan |
Rute |
Jarak Terbaik (km) |
|
1 |
Camani Kopi |
Crafted Coffee House |
Camani Kopi → Crafted Coffee House |
0.22 |
|
No |
Titik Awal |
Titik Tujuan |
Rute |
Jarak Terbaik (km) |
|
2 |
Camani Kopi |
Tan Panama |
Camani Kopi → Crafted Coffee House → Tan Panama |
0.33 |
|
3 |
Camani Kopi |
Sugesti Kopi |
Camani Kopi → Sugesti Kopi |
0.38 |
|
4 |
Camani Kopi |
Joglo Coffee Shop |
Camani Kopi → Crafted Coffee House → Tan Panama → Joglo Coffee Shop |
0.75 |
|
5 |
Crafted Coffee House |
Tan Panama |
Crafted Coffee House → Tan Panama |
0.11 |
|
6 |
Crafted Coffee House |
Sugesti Kopi |
Crafted Coffee House → Camani Kopi → Sugesti Kopi |
0.6 |
|
7 |
Crafted Coffee House |
Joglo Coffee Shop |
Crafted Coffee House → Tan Panama → Joglo Coffee Shop |
0.53 |
|
8 |
Tan Panama |
Sugesti Kopi |
Tan Panama → Crafted Coffee House → Camani Kopi → Sugesti Kopi |
0.71 |
|
9 |
Tan Panama |
Joglo Coffee Shop |
Tan Panama → Joglo Coffee Shop |
0.42 |
|
10 |
Sugesti Kopi |
Joglo Coffee Shop |
Sugesti Kopi → Joglo Coffee Shop |
0.53 |
Dari hasil pengujian dapat disimpulkan, bahwa program dibuat bisa menerima inputan berupa graph sehingga dapat menghitung rute terpendek, dan menampilkan rute terpendek beserta jaraknya.
Pada penelitian ini dikembangkan sebuah sistem yang berhasil diuji untuk menentukan rute terpendek menuju distributor kopi dengan menggunakan algoritma A Star. Hasil dari sistem ini menunjukkan bahwa pencarian rute terpendek pada peta menggunakan algoritma A Star dapat diwujudkan dalam bentuk graf. Setiap simpul grafik mewakili lokasi di peta, sedangkan ujungnya mewakili jalur yang menghubungkan lokasi tersebut. Setiap sisi graf memiliki bobot atau jarak yang digunakan untuk menghitung nilai heuristic. Setelah mendapatkan informasi jarak dan nilai heuristic, pencarian rute dilakukan menggunakan algoritma A Star menggunakan pohon pencarian dan antrian prioritas. Pada penelitian ini, dengan menggunakan algoritma A Star, sistem penentuan jalur terpendek dapat mengolah masukan graf, menghitung jalur terpendek, dan menampilkan hasil jalur terpendek beserta jaraknya. Misalnya, jika titik awal adalah Camani Kopi dan titik tujuan adalah Joglo Coffee Shop, maka jarak terpendek adalah 0,75 km pada rute Camani Kopi → Crafted Coffee House → Tan Panama → Joglo Coffee Shop.
Daftar Pustaka
-
[1] A. T. Putra, M. Rumani, B. Tt, and M. W. Paryasto, “PERBANDINGAN KOMPLEKSITAS
ALGORITMA A-STAR, FLOYD-WARSHALL, VITERBI PADA SDN (SOFTWARE
DEFINED NETWORKING).”
-
[2] R. Wafdan, M. Ihsan, and R. Zuhra, “Connectivity Algorithm in Simple Graphs,” Jurnal
Natural, vol. 14, no. 1, pp. 30–33, 2014.
-
[3] I. Bagus, G. Wahyu, and A. Dalem, “PENERAPAN ALGORITMA A* (STAR)
MENGGUNAKAN GRAPH UNTUK MENGHITUNG JARAK TERPENDEK,” Online, 2018. [Online]. Available: http://jurnal.stiki-indonesia.ac.id/index.php/jurnalresistor
-
[4] D. Teguh Yuwono and A. Fadlil, “Perbandingan Algoritma Breadth First Search dan
Depth First Search Sebagai Focused Crawler,” 2016. [Online]. Available: http://ars.ilkom.unsri.ac.id
-
[5] A. Ananda and N. Siregar, “Fakultas Komputer.”
-
[6] A. Adam Maulana, T. Informatika UDINUS, and F. Ilmu Komputer UDINUS,
“Implementasi Algoritma A* Dalam Aplikasi Berbasis Web untuk Menemukan Rute Terpendek sebagai Navigasi Peta Digital Indoor Implementation of A* Algorithm in WebBased Applications for Finding the Shortest Route as Navigation of Digital Indoor Map,” Universitas AMIKOM Yogyakarta, vol. 5, no. 1, 2017.
-
[7] S. Suhendri, Dede Abdurahman, and Dani Irfan Maulana, “IMPLEMENTASI
ALGORITMA A-STAR UNTUK PEMETAAN LOKASI SARANA KESEHATAN KABUPATEN MAJALENGKA BERBASIS GEOGRAPHIC INFORMATION SYSTEM (GIS),” INFOTECH journal, pp. 57–65, Sep. 2021, doi: 10.31949/infotech.v7i2.1512.
-
[8] S. Purnama, D. Ayu Megawaty, and Y. Fernando, “PENERAPAN ALGORITMA A STAR
(A*) UNTUK PENENTUAN JARAK TERDEKAT WISATA KULINER DI KOTA BANDARLAMPUNG,” Jurnal TEKNOINFO, vol. 12, no. 1, pp. 28–32, 2018.
-
[9] A. P. Graf, “Kajian Teori.”
Halaman ini sengaja dibiarkan kosong
1062
Discussion and feedback