Optimalisasi Keuntungan Menggunakan Metode Branch And Bound Pada Produksi Spring Bed
on
Jurnal Matematika Vol. 12, No.2, Desember 2022, pp. 78-88
Article DOI: 10.24843/JMAT.2022.v12.i02.p151
ISSN: 1693-1394
Optimalisasi Keuntungan Menggunakan Metode Branch and Bound Pada Produksi Spring Bed
Daryan Dali
Program Studi Matematika, Fakultas MIPA, Universitas Pattimura
Universitas Patiimura, Ambon, 97233, Indonesia
e-mail: daryanadali@gmail.com
Yopi Andry Lesnussa
Program Studi Matematika, Fakultas MIPA, Universitas Pattimura
Universitas Patiimura, Ambon, 97233, Indonesia e-mail: yopi_a_lesnussa@yahoo.com
Venn Yan Ishak Ilwaru
Program Studi Matematika, Fakultas MIPA, Universitas Pattimura
Universitas Patiimura, Ambon, 97233, Indonesia
e-mail: vennilwaru007@gmail.com
Abstract: PT Satelit Maluku is a company that produces spring beds with three types, namely 2in1, ordinary spring beds and single beds. Every company established aims to get big profits as well as PT Satelit Maluku. To obtain large profits, companies need to make strategies so that each available material can be allocated optimally and appropriately. The purpose of this research is PT Satelit Maluku can optimize the profit of spring bed production by using the Branch and Bound and QM for Windows V5 methods. From the results of calculations using the Branch and Bound method and QM for windows V5, the optimal profit is Rp. 19,775,000 with a lot of production of spring bed type 2in1 is 0 (not producing), ordinary spring bed is 26 pieces and single bed is 3 pieces.
Keywords: Optimization, Integer Linear Programming, Branch and Bound Method, QM for windows V5.
Abstrak: PT Satelit Maluku merupakan perusahaan yang memproduksi spring bed dengan tiga tipe, yaitu 2in1, spring bed biasa dan singgel bed. Setiap perusahaan yang didirikan bertujuan untuk mendapatkan keuntungan yang besar begitupun dengan PT Satelit Maluku. Untuk memperoleh keuntungan yang besar, perusaahaan perlu membuat strategi agar setiap bahan yang ada dapat di alokasikan dengan optimal dan tepat. Tujuan dari penelitian ini adalah PT Satelit Maluku dapat mengoptimalkan keuntungan produksi spring bed yang disusun ke model program linier integer kemudian diselesaikan menggunakan metode Branch and Bound dan QM for Windows V5. Dari hasil perhitungan menggunakan metode Branch and Bound dan QM for windows V5 di peroleh keuntungan optimal sebesar Rp.19.775.000 dengan banyak produksi spring bed tipe 2in1 adalah 0 (tidak memproduksi), spring bed biasa adalah 26 buah dan singgel bed adalah 3 buah.
Kata Kunci: Optimalisasi, Integer Linear Programming, Metode Branch and Bound, QM for windows V5
Spring bed adalah salah satu kebutuhan pokok yang sangat di butuhkan masyarakat untuk mendapatkan kenyamanan dalam beristirahat. Untuk memenuhi kebutuhan masyarakat tersebut khususnya masyarakat Maluku, PT Satelit Maluku hadir dengan produksi Spring bed yang berkualitas. Untuk mendapatkan keuntungan maksimal pihak perusahaan PT Satelit Maluku perlu melakukan strategi atau metode untuk menyelaraskan antara produksi dan kebutuhan pasar dengan memperhatikan keterbatasan yang dimiliki perusahaan. Untuk mengatasi masalah tersebut, dapat menggunakan metode program linier branch and bound.
Setiap perusahaan didirikan mempunyai tujuan memperoleh keuntungan, termasuk juga perusahaan PT Satelit Maluku. Untuk mencapai tujuan tersebut perusahaan harus mampu mengatur sedemikian rupa seluruh biaya yang digunakan agar tetap terkendali antara pengeluaran dan pemasukan perusahaan. Untuk mendapatkan keuntungan yang besar, sangat penting untuk menyelaraskan antara produksi dan permintaan pasar. Untuk mengatasi masalah tersebut, digunakan salah satu cabang ilmu matematika yaitu linear prigramming (Zahedi, 2010). Menurut Heizer dan Render (Heizer, J. & Render, B. 2006), sebagian besar permasalahan linear programming di dunia nyata memiliki lebih dari dua variabel yang mengakibatkan penyelesaian dengan metode grafik kurang efektif. Oleh karena itu, penyelesaian untuk permasalahan ini menggunakan metode simpleks. Metode simpleks adalah suatu metode yang secara sistematis dimulai dari suatu penyelesaian dasar yang fisibel ke pemecahan dasar fisibel lainnya, yang dilakukan berulang-ulang (iteratif) sehingga tercapai suatu penyelesaian optimum (Herjanto, 1999), (Nasution, dkk., 2016), (Budianto, dkk., 2017). Selain mencari solusi optimal, seringkali sangat berguna dilakukan suatu analisis untuk mengamati perubahan-perubahan yang terjadi pada koefisien fungsi tujuan dan konstanta ruas kanan fungsi kendala, serta dampaknya terhadap optimalitas. Analisis tersebut dinamakan analisis sensitivitas. Analisis sensitivitas menjelaskan sampai sejauh mana koefisien fungsi tujuan dan nilai ruas kanan kendala boleh berubah tanpa memengaruhi solusi optimal (Siswanto,2006). Hal ini berarti, dengan melakukan analisis sensitivitas, akibat yang mungkin terjadi dari perubahan-perubahan tersebut dapat diprediksi dan diantisipasi sebelumnya (Amirudin, 2012). Model dalam linier programming metode simpleks salah satunya memeperbolehkan variabel keputusannya berupa bilangan pecahan, artinya solusi tidak bulat oleh karena itu dapat diatasi dengan menggunakan optimisasi dengan solusi bulat yang disebut dengan integer programming. Integer linier programming terdiri dari Metode Branch and Bound (cabang dan batas) adalah salah satu metode untuk
menghasilkan penyelesaian optimal pemrograman linear yang menghasilkan variabel-variabel keputusan bilangan bulat (Siringoringo,2005), (Firmansyah, dkk., 2018). Integer Linear Programming bisa dipecahkan dengan banyak cara, antara lain dengan memanfaatkan grafik, dengan metode subtitusi dan eliminasi, dan sebagainya (Rumetna, dkk., 2018). Cara yang cukup efisien untuk memecahkan masalah program bilangan bulat dengan mengaplikasikan algoritma Branch and Bound dibandingkan metode perhitungan nilai bulat lainnya dan sudah menjadi kode komputer standar bagi Integer Linear Programming (RK Dg Pagiling, dkk., 2015). Metode Branch and Bound dapat dimanfaatkan untuk memecahkan suatu masalah Integer Linear Programming sebab hasil yang didapatkan dalam pemecahan masalah optimasi lebih akurat dan lebih baik dari metode lainnya. Metode ini mempunyai hasil optimal banyak dari metode lainnya sehingga penulis bisa menentukan mana hasil yang paling optimal dari hasil-hasil yang didapat, metode ini dikatakan lebih akurat dan lebih baik dibandingkan dari metode lainnya (Angeline, dkk., 2014), (Akram, dkk., 2016).
PT. Satelit Maluku meupakan perusahaan yang memproduksi spring bed dengan 3 tipe yaitu 2in1, spring bed biasa dan singgel bed. Perusahaan ini berlokasi di kebun cengkeh, desa Batu Merah, Kec. Sirimau, Ambon, Maluku, Indonesia. PT Satelit Maluku berdiri pada tahun 2011. PT Satelit Maluku adalah salah satu perusahaan besar yang ada di Ambon dan merupakan perusahaan produksi spring bed dengan banyak permintaan pasar. Oleh karena itu sangat penting untuk PT. Satelit Maluku harus memiliki perencanaan jumlah produksi untuk memenuhi permintaan pasar. Berdasarkan uraian pada paragraf sebelumnya terlihat bahwa PT Satelit Maluku membutuhkan metode yang dapat menjawab permasalah yang ada dan juga mendapatkan keuntungan optimal dengan metode yang telah di uraikan sebelumnya. Dengan demikian peneliti tertarik untuk mengambil judul “OPTIMALISASI KEUNTUNGAN MENGGUNAKAN METODE BRANCH AND BOUND PADA PRODUKSI SPRING BED”.
Data yang digunakan dalam penelitian ini yaitu data primer tentang produksi spring bed pada PT. Satelit Maluku. Data tersebut kemudian diolah dan dianalisis menggunakan metode simpleks dan metode Branch and Bound untuk mendapatkan keuntungan optimal dari proses produksi Spring bed. Adapun tahapan dalam penelitian ini adalah sebagai berikut:
-
1. Identifikasi Masalah,
-
2. Pemilihan model pemecahan masalah,
-
3. Pengumpulan data,
-
4. Implementasi model (metode simpleks dan metode branch and bound)
-
5. Implementasi software QM for Windows V5.
Data sprinng bed berdasarkan satu kali produksi pada bulan Agustus 2021, pada Tabel 1, berikut:
Tabel 1. Tipe Spring Bed
|
No. |
Tipe Spring Bed |
Ukuran |
|
1 |
2in1 |
200 x 120 |
|
2 |
Spring Bed Biasa |
200 x 160 |
|
3 |
Singgel Bed |
200 x 120 |
Berdasarkan data di atas maka dapat diformulasi dengan simbol x1,x2,%3 dan Z dengan; %1 = 2in1, X2=Spring Bed Biasa, X3=Singgel Bed dan Zmax = Jumlah Keuntungan (Keterangan : x1, X2, X3 adalah simbol untuk satuan produk). Bahan baku produksi spring bed dapat dilihat pada Tabel 2, berikut:
Tabel 2. Bahan baku dan tipe spring bed
|
Bahan Baku |
Tipe Spring Bed |
Persediaan |
Satuan | ||
|
2 in 1 |
Biasa |
Singgel Bed | |||
|
Per |
400 |
200 |
200 |
17.600 |
Buah |
|
Kayu |
24 |
14 |
12 |
400 |
Buah |
|
Paku |
92 |
48 |
46 |
10.500 |
Buah |
|
Kain |
4 |
2 |
2 |
500 |
Lembar |
|
Karpet |
4 |
2 |
2 |
500 |
Lembar |
|
Busa |
4 |
2 |
2 |
700 |
Lembar |
|
Keuntungan |
787.500 |
700.000 |
525.000 Rupiah | ||
Sumber data: PT Satelit Maluku
Dari Tabel 2 diatas dapat diformulasi kendala-kendala dari permasalahan program linier diatas sebagai berikut:
400 xi + 200X2 + 200 x3 ≤ 17.600
24 xi + 14 X2 +12X3 ≤ 400
92 xi + 48 X2+ 46 x3 ≤ 10.500
4 xi + 2 X2 +2 X3 ≤ 500
4 x1+ 2 x2 +2 x3 ≤ 500
4 xi + 2 X2 +2 X3 ≤700
%1,%2,⅞ ≥ 0
Berikut hasil dari penyelesaian linear proogrammig metode simpleks dengan menggunakan QM for Windows V5.
Objective
ff M aximize
C M inimize
|
Variable |
Status |
Value |
|
X1 |
NONBasic |
C |
|
X2 |
Basic |
28.5714 |
|
X3 |
NONBasic |
O |
|
slack 1 |
Basic |
11885.71 |
|
slack 2 |
NONBasic |
O |
|
slack 3 |
Basic |
9128.571 |
|
slack 4 |
Basic |
442.8571 |
|
slack 5 |
Basic |
442.8571 |
|
slack 6 |
Basic |
642.8571 |
|
Optimal Value (Z) |
20000000 |
Gambar 1. Solusi dengan menggunakan software QM for Windows V5
|
- Objective (∙ Maximize C Minimize |
Instruction There are more results available in additional windows. These may be opened I |
|
Cj |
Basic Variables |
787500 X1 |
700000 X2 |
525000 X3 |
O slack 1 |
O slack 2 |
O slack 3 |
O slack 4 |
O slack 5 |
O slack 6 |
Quantity |
|
Iteration 1 | |||||||||||
|
O |
slack 1 |
400 |
200 |
200 |
1 |
O |
O |
O |
O |
O |
17,600 |
|
O |
slack 2 |
24 |
14 |
12 |
O |
1 |
O |
O |
O |
O |
400 |
|
O |
slack 3 |
02 |
48 |
46 |
O |
O |
1 |
O |
O |
O |
10,500 |
|
O |
slack 4 |
4 |
2 |
2 |
O |
O |
O |
1 |
O |
O |
500 |
|
O |
slack 5 |
4 |
2 |
2 |
O |
O |
O |
O |
1 |
O |
500 |
|
O |
slack 6 |
4 |
2 |
2 |
O |
O |
O |
O |
O |
1 |
700 |
|
Zj |
O |
O |
O |
O |
O |
O |
O |
O |
O |
O | |
|
cj-zj |
787,500 |
700,000 |
525,000 |
O |
O |
O |
O |
O |
O | ||
|
Iteration 2 | |||||||||||
|
O |
slack 1 |
O |
-33.3333 |
O |
1 |
-16.6667 |
O |
O |
O |
O | |
|
787500 |
X1 |
1 |
0.5833 |
0.5 |
O |
0.0417 |
O |
O |
O |
O |
16.6667 |
|
O |
slack 3 |
O |
-5.6667 |
O |
O |
-3.8333 |
1 |
O |
O |
O |
8,966.6667 |
|
O |
slack 4 |
O |
-0.3333 |
O |
O |
-0.1667 |
O |
1 |
O |
O |
433.3333 |
|
O |
slack 5 |
O |
-0.3333 |
O |
O |
-0.1667 |
O |
O |
1 |
O |
433.3333 |
|
O |
slack 6 |
O |
-0.3333 |
O |
O |
-0.1667 |
O |
O |
O |
1 |
633.3333 |
|
Zj |
787500 |
459375 |
393750 |
O |
32812.5 |
O |
O |
O |
O | ||
|
cj-zj |
O |
240,625.0 |
131,250 |
O |
-32,812.5 |
O |
O |
O |
O | ||
|
Iteration 3 | |||||||||||
|
O |
slack 1 |
57.1429 |
O |
28.5714 |
1 |
-14.2857 |
O |
O |
O |
O | |
|
700000 |
X2 |
1.7143 |
1 |
0.8571 |
O |
0.0714 |
O |
O |
O |
O |
28.5714 |
|
O |
slack 3 |
9.7143 |
O |
4.8571 |
O |
-3.4286 |
1 |
O |
O |
O |
9,128.5714 |
|
O |
slack 4 |
0.5714 |
O |
0.2857 |
O |
-0.1429 |
O |
1 |
O |
O |
442.8571 |
|
O |
slack 5 |
0.5714 |
O |
0.2857 |
O |
-0.1429 |
O |
O |
1 |
O |
442.8571 |
|
O |
slack 6 |
0.5714 |
O |
0.2857 |
O |
-0.1429 |
O |
O |
O |
1 |
642.8571 |
|
Zj |
1200000 |
700000 |
600000 |
O |
50000 |
O |
O |
O |
O | ||
|
cj-zj |
-412,500 |
O |
-75,000 O |
O |
-50,000 |
O |
O |
O |
O | ||
Gambar 2. Iterasi metode simpleks dengan menggunakan software QM for Windows V5
Dengan metode simpleks diperoleh produksi spring bed tipe 2in1 adalah 0 (tidak produksi), spring bed biasa adalah 200 ≈ 28,571 dan singgel bed adalah 0 (tidak produksi) dengan keuntungan optimal sebesar Rp. 20.000.000, 00
Karena menggunakan metode simpleks di dapatkan solusi optimal yang tidak integer. Oleh karena itu akan di gunakan metode Branch and Bound untuk mendapatkan solusi optimal yang integer.
Pertama-tama akan ditentukan Batas Atas (BA) dan Batas Bawah (BB). berdasarkan hasil sebelumnya adalah xi = 0, x2 = 200 ≈ 28,571 dan x3 = 0 dengan keuntungan Rp.20.000.000,00 terlihat bawah x2 bukan bilangan integer oleh karena itu solusinya belum valid.
Karena x2 adalah satu-satunya variabel yang bernilai tidak integer maka x2 saja yang akan dicabangkan menjadi bagian-bagian masalah. Dengan tambahan kendala untuk bagian masalah 1 adalah x2 ≤ 28 dan bagian masalah 2 adalah x2 ≥ 29. Proses pencabangan dapat dilihat sebagai berikut :
Bagian masalah 1 : untuk x2 ≤ 28
Fungsi tujuan:
Zmax = 787.500x1+ 700.000 x2 + 525.000 x3
Fungsi kendala:
400 xi + 200X2 + 200 x3 ≤ 17.600
24 xi + 14 x2 +12x3 ≤ 400
92 xi + 48 x2 + 46 x3 ≤ 10.500
4 xi + 2 x2 +2 x3 ≤ 500
4 x1+ 2 x2 +2 x3 ≤ 500
4 xi + 2 x2 +2 x3 ≤700
x2 ≤ 28
Xj ≥ 0 , j= 1,2 dan 3
Diperoleh solusi dengan metode simpleks dengan menggunakan aplikasi QM for Windows V5 adalah :
x1 = 0, x2 = 28, x3 = 0,67 dan Z = 19.950.000
Bagian Masalah 2 : Untuk x2 ≥ 29
Fungsi tujuan:
Zmax = 787.500x1+ 700.000 x2 + 525.000 x3
Fungsi kendala :
400 xi + 200x2 + 200 x3 ≤ 17.600
24 xi + 14 x2+12x3 ≤ 400
92 xi + 48 x2 + 46 x3 ≤ 10.500
4 xi+ 2 x2 +2 x3 ≤ 500
4 xi + 2 x2 +2 x3 ≤ 500
4 xι + 2 X2 +2 X3 ≤700
X2 ≥ 29
xj≥0 , j= 1,2 dan 3
Diperoleh solusi dengan metode simpleks adalah infeasible.
Karena pada percabangan pada bagian masalah 1 Untuk x2 ≤ 28 masih bernilai tidak integer, maka percabangan tetap dilanjutkan sampai mendapatkan solusi optimal Z = Rp. 19.775.000, 00.
Berikut adalah prosedur metode branch and bound:
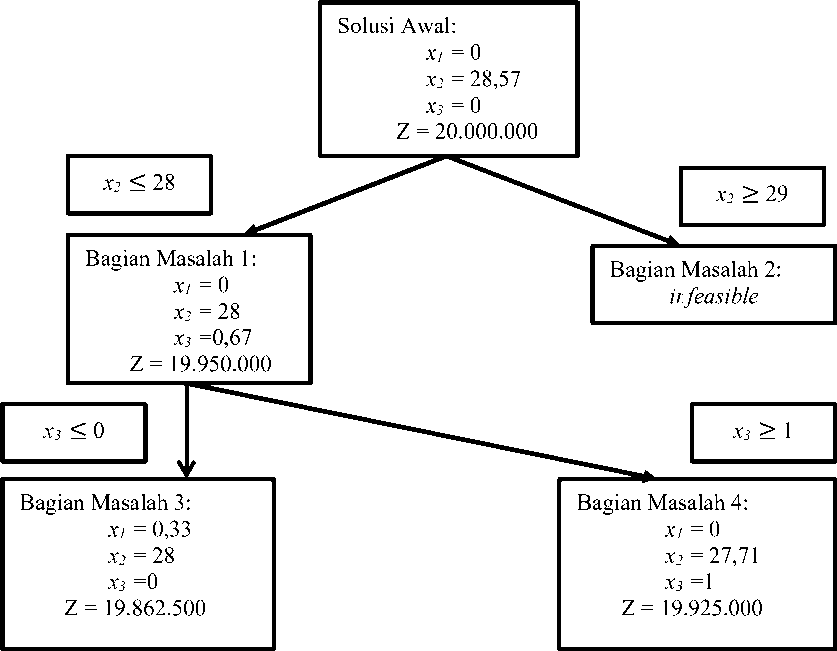
Bagian Masalah 4:
Bagian Masalah 3:
xι ≤ 0
Bagian Masalah 8: Infeasible
Bagian Masalah 7
Bagian Masalah 6
Bagian Masalah 5:
x1 = 0
x2 = 28
x3 =0
Z = 19.600.000
X2 ≥ 28
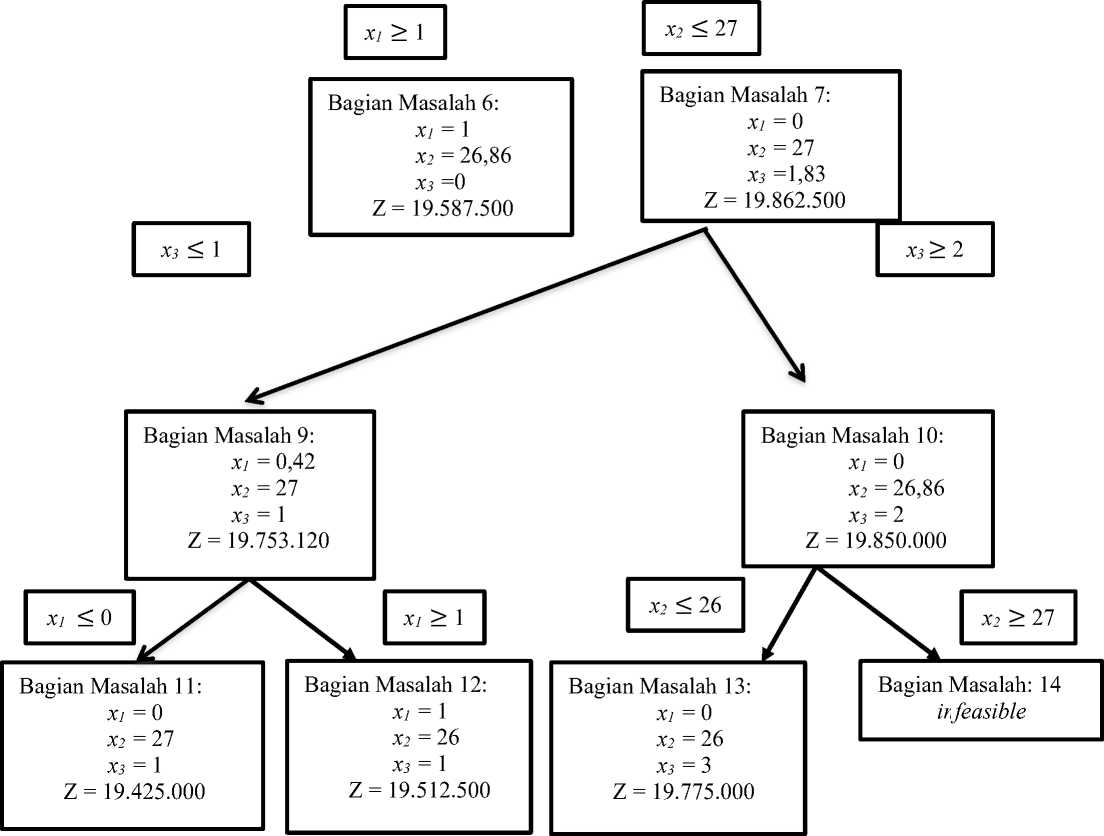
Gambar 2. Prosedur metode branch and bound
Jadi solusi optimal yang diperoleh dengan menggunakan metode branch and bound adalah Rp.19.775.000 dengan nilai variabel x1 = 0, x2 = 26 dan x3 = 3. Sehingga keputusan yang diperoleh adalah banyak produksi spring bed tipe 2in1 adalah 0 (tidak memproduksi), spring bed biasa adalah 26 buah dan singgel bed adalah 3 buah, dengan keuntungan optimal adalah Rp. 19.775.000
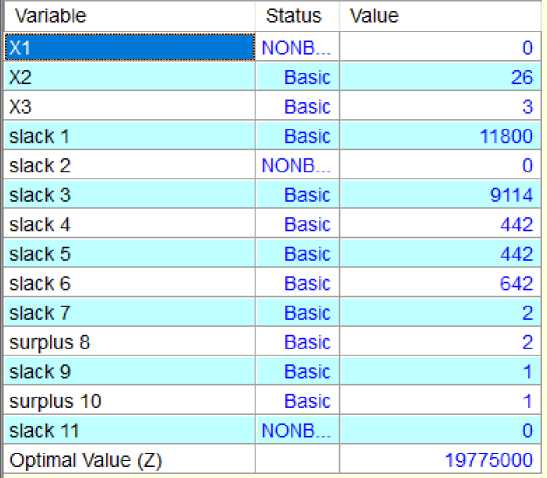
Gambar 3. Solusi optimal dengan QM for Windows V5
Adapun bahan yang dihabiskan untuk produksi adalah sebagai berikut : Per 11.800 buah dari 17600 buah persediaan, artinya ada 5.800 buah per sisa; Kayu 400 buah habis terpakai; Paku 9.114 buah dari 10500 buah persediaan, artinya ada 1.386 buah paku sisa; Kain 442 lembar dari 500 lembar persediaan, artinya ada 58 lembar kain sisa; Karpet 442 lembar dari 500 lembar persediaan, artinya ada 58 lembar karpet sisa dan Busa 642 karung dari 700 lembar persediaan, artinya ada 58 lembar busa sisa.
Berikut hasil dari penyelesaian integer linear proogrammig metode Branch and Bound dengan menggunjakan QM for Windows V5.
Iteration
Level
Xl
X2
X3
Solution
Value
Added Solution
constraint type
|
Optimal |
19775000 |
0 |
26 |
3 | |||
|
1 |
0 |
NONinteger |
20000000 |
0 |
28.57 |
0 | |
|
2 |
1 |
X2<= 28 |
NONinteger |
19350000 |
0 |
28 |
.67 |
|
3 |
2 |
X3<=0 |
NONinteger |
19862500 |
.33 |
28 |
0 |
|
4 |
3 |
X1<=0 |
INTEGER |
19600000 |
0 |
28 |
0 |
|
5 |
3 |
X1>= 1 |
Suboptimal |
19587500 |
1 |
26.86 |
0 |
|
6 |
2 |
X3>= 1 |
NONinteger |
19925000 |
0 |
27.71 |
1 |
|
7 |
3 |
X2<= 27 |
NONinteger |
19862500 |
0 |
27 |
1.83 |
|
S |
4 |
X3<= 1 |
NONinteger |
19753120 |
.42 |
27 |
1 |
|
9 |
5 |
X1<=0 |
Suboptimal |
19425000 |
0 |
27 |
1 |
|
10 |
5 |
X1>= 1 |
Suboptimal |
19512500 |
1 |
26 |
1 |
|
11 |
4 |
X3>=2 |
NONinteger |
19850000 |
0 |
26.86 |
2 |
|
12 |
5 |
X2<= 26 |
INTEGER |
19775000 |
0 |
26 |
3 |
|
13 |
5 |
X2>=27 |
Infeasible | ||||
|
14 |
3 |
X2>= 28 |
Infeasible | ||||
|
15 |
1 |
X2>= 29 |
Infeasible | ||||
Gambar 4. Iterasi metode Branch and Bound dengan QM for Windows V5
Berdasarkan pembahasan pada bab sebelumnya maka dapat di ambil kesimpulan bahwa Metode Branch and Bound dapat membantu dalam mengoptimalkan keuntungan pembuatan spring bed oleh PT Satelit Maluku dengan keterbatasan sumber daya yang ada. Dari hasil perhitungan menggunakan metode Branch and Bound dan QM for windows V5 diperoleh banyak produksi spring bed tipe 2in1 adalah 0 (tidak memproduksi), spring bed biasa adalah 26 buah dan singgel bed adalah 3 buah dengan keuntungan optimal yang didapatkan adalah sebesar Rp.19.775.000.
Daftar Pustaka
Akram Akram, Agusman Sahari, dan Agus Indra Jaya. (2016). Optimalisasi Produksi Roti Dengan Menggunakan Metode Branch and Bound (Studi Kasus Pada Pabrik Roti Syariah Bakery, Jl. Maleo, Lrg. VIII No. 68 Palu), Jurnal Ilmiah Matematika dan Terapan 13(2), 98-107.
Amirudin, A. (2012). Analisis Sensitivitas (Sensitivity Analysis).
Angeline Angeline, Iryanto Iryanto, dan Gim Tarigan. (2014). Penerapan Metode Branch and Bound dalam Menentukan Jumlah Produksi Optimum Pada CV. Xyz. Saintia Matematika, 2(2), 137–145.
Budiyanto, S. Mujiharjo, and S. Umroh. (2017). Maksimalisasi Profit pada Perusahaan Roti Bunda Bakery Menggunakan Metode Simplek. AGROINDUSTRI. vol. 7, 84– 98
Firmansyah, D. J. Panjaitan, M. Salayan, dan A. D. Silalahi. (2018). Pengoptimalan Keuntungan Badan Usaha Karya Tani di Beli Serdang dengan Metode Simpleks. J.Islam. Sci. Technol. 3(1), 18-28.
Heizer, J. dan Render, B. (2006). Operations Management: Manajemen Operasi. Penerjemah: Dwianoegrahwati Setyoningsih dan Indra Almahdy. Edisi Ketujuh. Jakarta: Salemba Empat.
Herjanto, E. (1999). Managemen produksi dan operasi. Edisi kedua. Jakarta: Grasindo.
M. S. Rumetna, T. N. Lina, T. Aponno, A. Palisoa, and F. Singgir. (2018). Penerapan Metode Simpleks Dan Software POM- QM Untuk Optimalisasi Hasil Penjualan Pentolan Bakso. Ilm. Manaj. Inform. dan Komput. 2(3), 143–149.
Nasution et al. (2016). PENERAPAN METODE SIMPLEKS UNTUK MENGANALISA PERSAMAAN LINIER DALAM MENGHITUNG KEUNTUNGAN MAKSIMUM. J. Ris. Komput. 3(4), 42–48.
RK Dg Pagiling, Agusman Sahari, dan Rais Rais. (2015). Optimalisasi Hasil Produksi Tahu dan Tempe Menggunakan Metode Branch and Bound (Studi Kasus: Pabrik Tempe Eri Jl. Teratai. No. 04 Palu Selatan). Jurnal Ilmiah Matematika dan Terapan, 12(1), 53-63
Siswanto. (2006). Operations Research. Jilid 1. Jakarta: Erlangga. an Operasi. Edisi Kedua. Jakarta: Grasindo
Zahedi. (2010). Metode Integer Linear Programming Melakukan Optimasi Produksi Di PT.NP Tbk. Jurnal.Jakarta
88
Discussion and feedback