Analisis Kestabilan Model Insidensi Setengah Jenuh pada Epidemi Flu Burung

Jurnal Matematika Vol. 11, No.2, Desember 2021, pp. 87-101

Article DOI: 10.24843/JMAT.2021.v11.i02.p139

ISSN: 1693-1394

Analisis Kestabilan Model Insidensi Setengah Jenuh pada Epidemi Flu Burung

Yomi Kharisma Septika

Kampus IPB, Jl. Raya Dramaga, Babakan, Kec. Dramaga, Kota Bogor, Jawa Barat 16680 e-mail: [email protected]

Ali Kusnanto

Kampus IPB, Jl. Raya Dramaga, Babakan, Kec. Dramaga, Kota Bogor, Jawa Barat 16680 e-mail: [email protected]

Paian Sianturi

Kampus IPB, Jl. Raya Dramaga, Babakan, Kec. Dramaga, Kota Bogor, Jawa Barat 16680 e-mail: [email protected]

Abstract: The H5N1 avian influenza is an example of a pathogen that is known to cause human disease outbreaks. This study focuses on selecting avian influenza control strategies using Half-Saturated Incidence (HSI) Models. In this study, a model was constructed by involving elements of human self-protection, poultry isolation and poultry vaccination. Furthermore, it is shown that the parameters that influence are the parameters of the population that apply personal protection and its effectiveness, the parameters of the rate of isolation of birds with avian influenza, and the parameters of vaccine coverage and its effectiveness. Increasing the value of this parameter can reduce the basic reproduction number so that disease-free conditions can occur. Hence, controlling the dynamics of disease spread can be done by increasing the value of these parameters.

Keywords: avian influenza, reproduction number, H5N1, half-saturated incidence

Abstrak: Flu burung H5N1 adalah contoh patogen yang diketahui sebagai penyebab terjadinya wabah penyakit pada manusia. Penelitian ini berfokus pada pemilihan strategi pengendalian penyakit flu burung dengan menggunakan Model Insidensi Setengah Jenuh (HSI). Dalam penelitian ini dikonstruksi model dengan pelibatan unsur perlindungan diri manusia, isolasi unggas dan vaksinasi unggas. Selanjutnya ditunjukkan bahwa parameter yang berpengaruh adalah parameter populasi yang menerapkan perlindungan diri dan efektivitasnya, parameter tingkat isolasi unggas yang terkena flu burung, serta parameter cakupan vaksin dan efektivitasnya. Peningkatan nilai parameter ini dapat menurunkan bilangan reproduksi dasar sehingga kondisi bebas penyakit dapat terjadi. Sehingga pengontrolan dinamika penyebaran penyakit dapat dilakukan dengan meningkatkan nilai parameter tersebut.

Kata Kunci: flu burung, bilangan reproduksi, H5N1, insidensi setengah jenuh flu burung, bilangan reproduksi, H5N1, insidensi setengah jenuh

• 1.    Pendahuluan

Penyakit adalah kondisi buruk pada organ atau bagian tubuh tertentu yang disebabkan oleh patogen atau mikroorganisme berbahaya seperti bakteri, virus, luka, dan munculnya sel tidak sempurna. Patogen yang menimbulkan penyakit dapat disebabkan oleh lingkungan yang kurang sehat dan individu lain karena sifatnya yang menular. Flu burung H5N1 adalah contoh patogen yang diketahui sebagai penyebab terjadinya wabah penyakit pada manusia dan penularannya terjadi secara langsung maupun tidak langsung (Hewajuli dan Dharmayanti, 2014).

Menurut OIE (2011), kasus flu burung H5N1 di Indonesia pertama kali dilaporkan pada 2 Februari 2004 dengan total 710 unggas mati. Dengan demikian pendekatan pemodelan sangat penting untuk pengambilan keputusan tentang strategi pengendalian penyakit flu burung H5N1. Pemodelan epidemiologi penyakit menular flu burung H5N1 yang digunakan adalah model SI yang mengkategorikan individu dalam suatu populasi sebagai kelompok yang rentan terhadap penyakit (Susceptible) dan terinfeksi penyakit (Infected) dimana tingkat insidensi jenuh (Saturated Incidence/SI) sering digunakan dalam model epidemik.

Pemodelan matematika dengan tingkat insidensi setengah jenuh digunakan oleh Chong et al. (2014) untuk menggambarkan manusia rentan yang melakukan kontak efektif dengan burung ataupun manusia terinfeksi dengan mempertimbangkan efek penghambatan dari perubahan perilaku ataupun tindakan pengendalian yang diambil oleh manusia rentan. Tingkat insidensi setengah jenuh juga dipilih karena adanya pertimbangan efek kejenuhan (saturation effect). Dengan kata lain, ketika populasi terinfeksi meningkat atau mencapai titik jenuh, maka laju infeksi penyakit mengalami perlambatan (Ulfa, 2020).

Selanjutnya, Lee dan Lao (2018) mempelajari dinamika global penyebaran penyakit flu burung dengan tingkat insidensi bilinear dan insidensi setengah jenuh pada burung dan manusia. Berkaitan dengan hal tersebut, dalam penelitian ini akan dilakukan analisis model penyebaran penyakit flu burung dengan tingkat insidensi setengah jenuh. Selain itu, akan diberikan beberapa strategi penanganan untuk mencegah atau mengurangi penyebaran penyakit flu burung seperti penerapan perlindungan diri oleh manusia, isolasi unggas, dan vaksinasi unggas. Harapannya salah satu strategi yang disebutkan dapat membantu mengontrol penyebaran penyakit flu burung H5N1.

• 2.    Metode Penelitian

Metode yang digunakan dalam penelitian ini adalah dengan melakukan rekonstruksi model yang telah dikembangkan oleh Lee dan Lao (2018). Selanjutnya pengembangan

model dilakukan dengan beberapa strategi yaitu: perlindungan diri manusia, isolasi unggas, dan vaksinasi unggas. Dalam penelitian ini, setiap strategi akan memunculkan kompartemen baru sehingga menghasilkan model matematika yang baru. Sehingga fokus utama penelitian ini adalah membandingkan dinamika solusi empat model tersebut terhadap perubahan nilai parameter.

Langkah yang dilakukan dalam membandingkan empat model tersebut adalah dengan melihat kestabilan titik tetap, menentukan bilangan reproduksi dasar (#0) dan mengamati pengaruh parameter pada dinamika populasi manusia dan burung.

Bilangan reproduksi dasar (dilambangkan dengan #₀) didefinisikan sebagai nilai yang diharapkan terjadi infeksi dalam suatu populasi yang sangat rentan yang dihasilkan oleh individu terinfeksi. Untuk mencari #₀ akan digunakan matriks next generation. Menurut Driessche dan Watmough (2002), klasifikasi bilangan reproduksi dasar, #₀ dibagi menjadi :

• 1.    Jika #₀ < 1, maka jumlah individu yang terinfeksi penyakit akan mengalami penurunan pada setiap waktu, sehingga penyakit tidak akan menyebar dalam suatu populasi.

• 2.    Jika ^₀ > 1, maka jumlah individu yang terinfeksi penyakit akan mengalami peningkatan pada setiap waktu, sehingga penyakit akan menyebar dalam suatu populasi.

• 3.    Hasil dan Pembahasan

  • 3.1    Model Matematika

Model I : Model Dasar

Model Flu burung yang digunakan dalam penelitian ini dikembangkan oleh Lee dan Lao (2018). Interaksi antara manusia dan burung dan antar burung menggunakan model insidensi setengah jenuh (Half-Saturated Incidence/HSI). Populasi manusia terbagi menjadi S_h, populasi manusia rentan (Susceptible) dan I_h, populasi manusia terinfeksi (Infected). Sedangkan populasi burung terbagi menjadi dua kelas yaitu S_b, populasi burung yang berisiko tertular penyakit (Susceptible) dan Ib, populasi burung yang terinfeksi parasit (Infected). Total populasi manusia dilambangkan dengan Nh dan total populasi burung dilambangkan dengan Nb. Secara skematis, model ini dapat digambarkan dalam diagram kompartemen pada Gambar 1a.

Model II : Penerapan Perlindungan Diri oleh Manusia

Kurangnya perlindungan diri seperti mengonsumsi unggas yang terinfeksi dan tidak dimasak dengan matang, terpapar debu infeksi, dan kebersihan lingkungan yang buruk adalah beberapa kemungkinan penyebab tertularnya penyakit flu burung H5N1. Oleh karena itu, penerapan perlindungan diri diperlukan oleh manusia untuk meminimalisir tingkat penyebaran penyakit. Selanjutnya, akan diperiksa efek penerapan perlindungan diri dalam mengendalikan transmisi penyakit pada manusia dengan mengubah parameter βbh menjadi (1 - cq)β_bh∙ Kemudian model mengalami modifikasi dan digambarkan ulang ke dalam diagram kompartemen pada Gambar 1b.

Model III : Isolasi Unggas

Pada strategi ini ditambahkan kompartemen baru yaitu populasi burung yang diisolasi (dilambangkan dengan T_b(t)) dan burung yang pulih (dilambangkan dengan R_b(t)). Dikarenakan isolasi burung tidak berpengaruh terhadap penularan penyakit pada populasi manusia, maka akan dipertimbangkan populasi unggas saja. Namun, untuk menyelidiki bagaimana strategi isolasi unggas bekerja untuk meminimalkan penyebaran penyakit, maka banyaknya burung yang terinfeksi per satuan waktu mengalami modifikasi. Selain itu, juga ditambahkan γ_b (tingkat kepulihan unggas yang terinfeksi) dan ψ_b (tingkat isolasi unggas yang terinfeksi). Kemudian model mengalami modifikasi dan digambarkan ulang ke dalam diagram kompartemen pada Gambar 1c.

Model IV : Vaksinasi Unggas

Untuk mencegah penyebaran penyakit pada hewan, para peneliti telah mengembangkan vaksin virus flu burung H5N1. Oleh karena itu, akan diterapkan program vaksinasi sebagai strategi pengendalian terhadap unggas. Kemudian akan ditambahkan kompartemen baru mewakili dinamika unggas yang divaksinasi (direpresentasikan oleh V_b(t)). Selanjutnya, akan dilakukan modifikasi terhadap banyaknya burung yang rentan dan terinfeksi per satuan waktu dengan menambahkan parameter persentase unggas yang divaksinasi (dilambangkan dengan p) dan tingkat kemanjuran vaksinasi unggas (dilambangkan dengan φ). Asumsi vaksinasi dapat mengurangi kemungkinan tertular flu burung sebesar 50% dibandingkan populasi unggas rentan yang tidak mendapatkan vaksinasi. Kemudian model mengalami modifikasi dan digambarkan ulang ke dalam diagram kompartemen pada Gambar 1d.

a. Kompartemen model I

b. Kompartemen model II

d. Kompartemen model IV

c. Kompartemen model III

Gambar 1. Diagram Kompartemen

Sistem persamaan diferensial yang digambarkan dalam diagram kompartemen di atas, dapat dituliskan dalam persamaan-persamaan berikut :

dSb              βbSbIb

7 — -d b   UbSb    :     ~,

dt                hb + Ib

dSb

“ — Ab ^bSb

βbSb!b hb + Ib

dlb βbSbIb

dt Jib + Ib

^- (⅛ + Sb)l_v

dSh _ _{λ c} PbhSbJb : — Λh [IhSh :     ”,

^dt            ⅛₁ + 4

(1)

di b dt

βbSbIb

⅛ +/b

~ (⅛ + Sb)I_b,

dSh

— = Λh-μhSh-(I — cq)

TT

T+¹ b

(2)

^⁼?TT-^^+d)A'

dl_h        PTJ_h

^dt       T+¹ b

-T+‘P T

Sistem Persamaan Diferensial

Model I

Sistem Persamaan Diferensial Model II

dSb               βbSbIb

7 -- ^li WbiSb 7     7”*

dt                 Λb 4^- /b

dlb βbSb!b _{r            x}

TΓ1^7b-^^+δb+^

dSb                       βbSbIb

77- J¹ “ P^^ - μ_bS_b - y—, O t                           ∏b^∖^lb

dTb                   ,

-^=ψiJ_b- (⅛+ ½+∕b) Tb,

(3)

dVb                _λ βvVbIb

— = pΛ_b-^-_φ}-- ^V_h,

(4)

dRb

— = γbT_b-μ_bRb,

dlb βbS_blb , BvVbIb ,

λ^≡ ^{+ 0}^⅛-⅛^a⅛

Sistem Persamaan Diferensial

Model III

Sistem Persamaan Diferensial

Model IV

Keterangan :

S_b(t): Banyaknya burung yang rentan pada waktu t I_h (t): Banyaknya burung yang terinfeksi pada waktu t S_h (t): Banyaknya manusia yang rentan pada waktu t I_h (t): Banyaknya manusia yang terinfeksi pada waktu t T_b(t): Banyaknya burung yang diisolasi pada waktu t R_b (t): Banyaknya burung yang pulih pada waktu t V_h (t) : Banyaknya burung yang divaksinasi pada waktu t ^_b (t): Banyaknya populasi burung pada waktu t N_b(t): Banyaknya populasi manusia pada waktu t S_b (0): Banyaknya burung yang rentan pada waktu t = 0 I_b (0): Banyaknya burung yang terinfeksi pada waktu t = 0 S_h (0): Banyaknya manusia yang rentan pada waktu t = 0 I_h (0): Banyaknya manusia yang terinfeksi pada waktu t = 0 T_h (0): Banyaknya burung yang diisolasi pada waktu t = 0 R_h (0): Banyaknya burung yang pulih pada waktu t = 0 V(0): Banyaknya burung yang divaksinasi pada waktu t = 0

∕_h: Laju kelahiran burung

∕_h: Laju kelahiran manusia

μ_b: Laju kematian alami burung

μ_h: Laju kematian alami manusia

β_b: Tingkat penularan penyakit pada burung β_h: Tingkat penularan penyakit dari burung ke manusia

R_b: Konstanta setengah jenuh untuk burung tertular flu burung

R_{b ft}: Konstanta setengah jenuh untuk manusia tertular flu burung dari unggas yang terinfeksi d : Laju kematian akibat penyakit flu burung pada manusia

d_b: Laju kematian akibat penyakit flu burung pada burung

• q: Tingkat efisiensi perlindungan diri

• c: Persentase populasi manusia yang menerapkan perlindungan diri

• y_h:    Tingkat kepulihan unggas

^_h: Tingkat isolasi unggas

β_v: Tingkat penularan penyakit pada burung yang divaksinasi

R_v: Konstanta setengah jenuh untuk burung yang divaksinasi tertular flu burung

φ: Tingkat kemanjuran vaksinasi

p : Persentase populasi unggas yang divaksinasi

• 3.2    Titik Tetap dan Bilangan Reproduksi Dasar

Model I

Titik tetap bebas penyakit, ^o _ ^ 0 ^ 0 ^ 0 j o^ _ (^b q ⅞ qA ^{b , b , h , h}       ∖μ_b' 'μ_h' /

Titik tetap endemik, E* = (S_b*,I_b*,S_h*,I_h*)

dengan

„ * _ ^hb(μb ⁺ ^b) ⁺ ^b

^Sb =    (μb+βb)   '

I * _ ^b^βb ^{- μ}b^hb(μb ⁺ ^b) ^b     (μb ⁺ ^b)(μb ^{+ β}b)

S * ___________^ħ[^hbh(^μb + ^b)(μb + βb) ⁺ ^b^βb ^{- μ}b^hb(μb + ^b)__________

-

^μb(^μb ⁺ ^b)[^μh^hbh ^{- h}b(μh ^{+ β}bh) ^{+ β}b[^b^βbh ^{+ μ}h[^hbh(μb + ^b) ⁺ ^b]l

I * _ _____________________^[>bh[Ab ^β b^-μbhb(^μ_b+δ_b)]______________________

^[μb(μb^+δb⁾[μh^hbh^-hb(μh+βbh⁾]^+βb^[Λb^βbh⁺μh[hbh(μb+δb⁾+Λb]^]](d+μh⁾

di mana konstanta A_bβ_b > μ_bh_b(μ_b + δ_b).

Bilangan reproduksi dasar, ^ _    ^bβb

0    ^μb^hb(μb+δb)

Model II

Titik tetap bebas penyakit, ^ o _^o ^o ^o ^ o^_ Λbn. Q Λ⅛ q^

Titik tetap endemik, e_pp* = (S_b*,I_b*,S_h*,I_h*)

dengan :

* -^hb(μb ⁺ ^b^{β +} Λ

^Sb =

(^μb ^{+ β}b)

b

,

I * _ ^b^βb — ^μb^hb(μb ⁺ δb) ^b     (μb ⁺ δb)(μb ^{+ β}b)

S * =_____________^ΛhEbhμμ+^δμ⁾⁽.μμ+^β2+^Λ.b^β-μb^bbiμμ+^δμL_____________,

^{b     μ}b(μb^+δb)[μh^bbh^-bbμh⁺(cq-l)^βbh^bb]^+βb[(Λb-ΛbCq)^βbh+μh[hbh(μ_b+δ_b)+Λb]]

Ih = —

___________________________^Λh(^cq-^1)βbh[Λbβb-μbhb(^μh+δh⁾]___________________________ [^μb(μb⁺βb)[μh^bbh^-bbμh⁺(cq-l)hb^βbh]^+βb[CΛ_b-Λ_bcq)^β_bh⁺μh[h_bh(μ_b+δ_b)+Λ_b]]](d+^μh)

di mana konstanta Λ_bβ_b > μ_bh_b(μ_b + δ_b)∙

Bilangan reproduksi dasar,

Rpd

(1-cq)Λhβbh μh^hbh(μb+δb)

Model III

Titik tetap bebas penyakit,ι^pθ   (Sb¹Jb¹J^plJ^pH   {~,o^^

Titik tetap endemik, e_i* = (S_b*, I_b*, T_b*, R_b*) dengan :

_c *   ^hb(fib ^{+ S}b ^{+ ψ}b) + ^A

b

,

^b =

(fib ^{+ β} b)

I * _ Ab^βb ^{- fi}bhb(μb + Sb +Ψb)

^b     (μb + ^sb ⁺ Ψb)(fib ^{+ β}b)

T * _   Λb^β_bΨb ^{- fi}b^hb^ψb(fib ^{+ S}b ^{+ ψ}b)

^b    (fib + ^sb ^{+ ψ}b)(fib ^{+ β}b)(fib ^{+ S}b ⁺ Yb)

^r*=X⅛^p^^

di mana konstanta A_bβ_b > μ_bh_b(μ_b + S_b+ ψ_b).

Bilangan reproduksi dasar, ^ _     ^bPb

^{1    μ}b^hb(μb+δb⁺Ψb)

Model IV

Titik tetap bebas penyakit, ^  0 _ ^ 0 y 0 ∣ o^ _ ((.ι-p^)Λ_b P ^b ^ θλ

^{b , b , b p} μ_b ’ μ_b ’ /

Bilangan reproduksi dasar, ^   _    Λ_b    Γ(ι-p)β_b ψ ∩ _ a Pv p!

Pb(Pb⁺Sbi)    ^hb                 ħv 1

• 3.3    Simulasi Numerik
  
  Model I

Simulasi numerik dilakukan dengan menggunakan nilai parameter seperti terlihat pada Tabel 1.

Tabel 1. Nilai		parameter dari model
Parameter	Nilai	Parameter	Nilai
^b	ι.00o individu per hari 365	d	_______6_______per hari (108 x 106) x 912.5
^h	is.59 w⅛(0) per hari 365 x 1000	hb	1.405 individu
Vb	1   per hari 2 x 365	hbh	20.000 individu
Vh	1    per hari 67.4x365	Sb(O)	2.279 burung
βb	710   per hari 4.709x30	Zb(O)	300 burung
βbh	_______16_______per hari (108 x 106) x 912.5	Sh(O)	22.675 manusia
Sb	817   per hari 4.709x30	Zh(O)	0 manusia

Dengan melakukan substitusi nilai parameter pada Tabel 1 ke dalam model, maka akan diperoleh grafik dinamika populasi pada model HSI seperti dalam Gambar 2 berikut :

Gambar 2. Dinamika populasi pada model HSI

Dalam kondisi ini titik tetap endemik bersifat stabil sehingga penyakit masih ada di dalam populasi. Untuk menanggulanginya, akan disusun strategi-strategi seperti dalam Model II, Model III, dan Model IV.

Model II

Simulasi numerik dilakukan dengan menambah nilai parameter c dan q. Simulasi pengaruh persentase populasi manusia yang menerapkan perlindungan diri terhadap dinamika penyebaran penyakit dilakukan menggunakan nilai parameter sesuai pada Tabel 1. Hal ini dapat dijelaskan melalui hasil simulasi dengan perubahan nilai parameter q yang disajikan pada Tabel 2.

Tabel 2. Hasil simulasi perubahan nilai parameter c

Nilai parameter q	Nilai parameter c	^PD
0.1	0.000001	1.08253
0.1	0.1	1.07171
0.1	0.3	1.05006
0.1	0.5	1.02841
0.1	0.8	0.99593
0.1	0.9	0.985105

Berdasarkan Tabel 2, diperoleh ^_pd > 1 untuk c yang bernilai 0.000001,0.1,0.3, dan 0.5 yang menghasilkan titik kestabilan endemik yang bersifat stabil. Selain itu, diperoleh ^PD < 1 untuk c yang bernilai 0.8 dan 0.9 yang menghasilkan titik kestabilan bebas penyakit yang bersifat sadel. Dinamika populasi manusia terinfeksi dari perubahan nilai parameter c dilihat dapat pada Gambar 3.

Gambar 3. Dinamika populasi manusia terinfeksi akibat perubahan nilai c

Hasil simulasi pada perubahan parameter c menunjukkan bahwa pada saat c ditingkatkan dari 0.5 sampai 0.8 akan menurunkan #_pD dari 1.02841 sampai 0.99593. Pada kasus ini, batas untuk terjadinya endemik maupun bebas penyakit dapat ditentukan secara analitik yaitu ketika c sebesar 0.762402 dengan asumsi nilai parameter lain tetap.

Simulasi pengaruh tingkat efisiensi perlindungan diri terhadap dinamika penyebaran penyakit dilakukan menggunakan nilai parameter sesuai pada Tabel 1. Hal ini dapat dijelaskan melalui hasil simulasi dengan perubahan nilai parameter q yang disajikan pada Tabel 3.

Tabel 3. Hasil simulasi perubahan nilai parameter q

Nilai parameter c	Nilai parameter q	^PD
0.1	0.000001	1.08253
0.1	0.1	1.07171
0.1	0.3	1.05006
0.1	0.5	1.02841
0.1	0.8	0.99593
0.1	0.9	0.985105

Berdasarkan Tabel 3, untuk q yang bernilai 0.000001,0.1,0.3, dan 0.5 menghasilkan nilai S_pd > 1 dan titik tetapnya bersifat stabil, sedangkan untuk q yang bernilai 0.8 dan 0.9 menghasilkan nilai S_pd < 1 dan titik tetapnya bersifat sadel. Dinamika populasi manusia terinfeksi dari perubahan nilai parameter q dapat dilihat pada Gambar 4.

Gambar 4. Dinamika populasi manusia terinfeksi akibat perubahan nilai q

Hasil simulasi pada perubahan parameter q menunjukkan bahwa pada saat q ditingkatkan dari 0.5 sampai 0.8, maka akan menurunkan S_pd dari 1.02841 sampai 0.99593. Pada kasus ini, batas untuk terjadinya endemik maupun bebas penyakit dapat ditentukan secara analitik ketika q sebesar 0.762402 dengan nilai parameter lain tetap.

Model III

Simulasi numerik dilakukan untuk memperlihatkan dinamika solusi dengan nilai parameter yang digunakan adalah ψ_b dimana nilai ψ_b berubah-ubah dengan nilai parameter lainnya dibuat tetap. Asumsi nilai awal T_b (0) = 0 dan R_b(0) = 0.

Simulasi pengaruh tingkat isolasi unggas terhadap dinamika penyebaran penyakit dilakukan menggunakan nilai parameter ψ_b = [0,1]. Hal ini dapat dijelaskan melalui hasil simulasi dengan perubahan nilai parameter ψ_b yang disajikan pada Tabel 4.

Tabel 4. Hasil simulasi perubahan nilai parameter ψ_b

Nilai parameter ψh	Si
0.000001	1.00001
0.1	0.0667663
0.3	0.023292
0.5	0.0141066
0.8	0.00886352
0.9	0.00788645

Berdasarkan Tabel 4, diperoleh Sj >1 untuk ψ_b yang bernilai 0.000001 yang menghasilkan titik kestabilan endemik yang bersifat stabil. Selain itu, diperoleh Sj < 1

untuk ψ_b yang bernilai 0.1,0.3,0.5,0.8, dan 0.9 yang menghasilkan titik kestabilan bebas penyakit yang bersifat stabil. Dinamika populasi burung diisolasi dari perubahan nilai parameter ψ_b dapat dilihat pada Gambar 5.

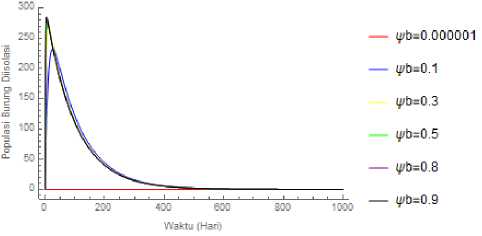
Gambar 5. Dinamika populasi burung diisolasi akibat perubahan nilai ψ_b

Hasil simulasi pada perubahan parameter φ_b menunjukkan bahwa pada saat ^ ditingkatkan dari 0.000001 sampai 0.1, maka akan menurunkan ^₁ dari 1.00001 sampab 0.0667663. Pada kasus ini, batas untuk terjadinya endemik maupun bebas penyakit dapat ditentukan secara analitik yaitu ketika populasi burung yang diisolasi sebesar 0.00000110144 dengan asumsi nilai parameter lain tetap.

Model IV

Simulasi numerik dilakukan dengan menambah nilai parameter p dan φ. Simulasi pengaruh persentase populasi burung yang divaksinasi terhadap dinamika penyebaran penyakit dilakukan menggunakan nilai parameter sesuai pada Tabel 1 dengan asumsi nilai awal kj,(0) = 0. Hal ini dapat dijelaskan melalui hasil simulasi dengan perubahan nilai parameter p yang disajikan pada Tabel 5.

Tabel 5. Hasil simulasi perubahan nilai parameter p

Nilai parameter φ	Nilai parameter p	^Vb
0.1	0.000001	1.00015
0.1	0.1	0.974535
0.1	0.3	0.923296
0.1	0.5	0.872058
0.1	0.8	0.795201
0.1	0.9	0.769581

Berdasarkan Tabel 5, diperoleh ^_vb > 1 untuk p yang bernilai 0.000001 yang menghasilkan titik kestabilan endemik yang bersifat stabil. Selain itu, diperoleh ^_vb < 1 untuk p yang bernilai 0.1,0.3,0.5,0.8, dan 0.9 menghasilkan titik kestabilan bebas

penyakit yang bersifat stabil. Dinamika populasi burung divaksinasi dari perubahan nilai parameter p dapat dilihat pada Gambar 6.

Gambar 6. Dinamika populasi burung divaksinasi akibat perubahan nilai p

Hasil simulasi pada perubahan parameter p menunjukkan bahwa pada saat p ditingkatkan dari 0.000001 sampai 0.1, maka akan menurunkan ^_vb dari 1.00015 sampai 0.974535. Pada kasus ini, batas untuk terjadinya endemik maupun bebas penyakit dapat ditentukan secara analitik yaitu ketika p sebesar 0.000390381 dengan asumsi nilai parameter lain tetap.

Simulasi pengaruh tingkat kemanjuran vaksinasi terhadap dinamika penyebaran penyakit dilakukan menggunakan nilai parameter sesuai pada Tabel 1. Hal ini dapat dijelaskan melalui hasil simulasi dengan perubahan nilai parameter φ yang disajikan pada Tabel 6.

Tabel 6. Hasil simulasi perubahan nilai parameter φ

Nilai parameter p	Nilai parameter φ	^Vb
0.0002	0.000001	1.00012
0.0002	0.1	1.0001
0.0002	0.3	1.0007
0.0002	0.5	1.00004
0.0002	0.8	0.999987
0.0002	0.9	0.99997

Berdasarkan Tabel 6, untuk φ yang bernilai 0.000001,0.1,0.3, dan 0.5 menghasilkan nilai ^_vb > 1 dan titik tetap endemik bersifat stabil, sedangkan untuk φ yang bernilai 0.8 dan 0.9 menghasilkan nilai ^_vb < 1 dan titik tetap bebas penyakit bersifat stabil. Dinamika populasi burung divaksinasi dari perubahan nilai parameter φ dapat dilihat pada Gambar 7.

Gambar 7. Dinamika populasi burung divaksinasi akibat perubahan nilai φ

Hasil simulasi pada perubahan parameter φ menunjukkan bahwa pada saat φ ditingkatkan dari 0.5 sampai 0.8, maka akan menurunkan ^_vb dari 1.00004 sampai 0.999987. Pada kasus ini, batas untuk terjadinya endemik maupun bebas penyakit dapat ditentukan secara analitik yaitu ketika φ sebesar 0.394992 dengan asumsi nilai parameter lain tetap.

4. Kesimpulan dan Saran

Kesimpulan

Pada penelitian ini dilakukan analisis model Insidensi Setengah Jenuh (HSI) dan diperoleh hasil bahwa model memiliki titik tetap bebas penyakit dan titik tetap endemik. Titik tetap bebas penyakit bersifat stabil asimtotik lokal jika bilangan reproduksi dasar yang diperoleh bernilai kurang dari satu dan titik tetap endemik bersifat stabil asimtotik lokal jika bilangan reproduksi dasar yang diperoleh bernilai lebih dari satu.

Pada simulasi numerik strategi perlindungan diri terlihat bahwa jika parameter populasi manusia yang menerapkan perlindungan diri dan tingkat keefektifannya ditingkatkan maka dapat menurunkan bilangan reproduksi dasar. Kedua parameter tersebut sama cepatnya dalam membuat populasi menuju keadaan endemik. Dinamika penyebaran penyakit dapat dikontrol dengan menambah populasi manusia yang menerapkan perlindungan diri atau dengan menambah tingkat keefektifannya. Batas nilai kedua parameter dapat ditentukan secara analitik dan diperoleh hasil bahwa kedua parameter tersebut memiliki hubungan linear.

Pada simulasi numerik strategi isolasi unggas terlihat bahwa jika parameter tingkat isolasi unggas ditingkatkan maka dapat menurunkan bilangan reproduksi dasar. Dinamika penyebaran penyakit dapat dikontrol dengan menambah tingkat isolasi unggas. Batas nilai parameter tersebut dapat ditentukan secara analitik yaitu dengan menghitung batas perubahan nilai bilangan reproduksi dasarnya untuk menentukan terjadinya kejadian bebas penyakit atau endemik.

Pada simulasi numerik strategi vaksinasi unggas terlihat bahwa jika parameter populasi unggas yang divaksinasi dan tingkat kemanjurannya ditingkatkan maka dapat menurunkan bilangan reproduksi dasar. Dinamika penyebaran penyakit dapat dikontrol dengan menambah populasi unggas yang divaksinasi atau dengan menambah tingkat kemanjuran vaksinasi. Batas nilai kedua parameter dapat ditentukan secara analitik dan diperoleh hasil bahwa kedua parameter tersebut memiliki hubungan tak linear. Populasi unggas yang divaksinasi lebih cepat membuat populasi menuju keadaan endemik dibandingkan tingkat kemanjuran vaksinasi. Hal ini dikarenakan betapa pun tingkat kemanjuran vaksin tersebut, jika mayoritas populasi tidak divaksinasi, maka akan sulit untuk mengontrol dan mencegah penularan penyakit infeksi.

Saran

Penelitian ini diharapkan dapat dikembangkan lebih lanjut dengan penambahan asumsi populasi burung yang tidak tertutup, yaitu adanya migrasi yang terjadi di dalam populasi burung.

Ucapan Terima Kasih

Penulis mengucapkan terima kasih kepada Departemen Matematika IPB yang telah memberi dukungan financial terhadap penelitian/makalah ini.

Daftar Pustaka

Chong, N.S., Tchuenche, J.M., & Smith, R.J. (2014). A Mathematical Model of Avian

Influenza with Half-Saturated Incidence. Theory in Biosciences,133(2014), 23-38.

Driessche, P.V.D., Watmough, J. (2002). Reproduction Numbers and Sub-Threshold Endemic Equilibria for Compartmental Models of Disease Transmission.

Mathematical Biosciences, 180(2002), 2948.

Hewajuli, D.A., & Dharmayanti, N.L.P.I. (2014). Identifikasi Flu Burung H5N1 pada Unggas di Sekitar Kasus Flu Burung pada Manusia Tahun 2011 di Bekasi. Jurnal Veteriner,15(1), 68-78.

Lee, H., & Lao, A. (2018). Transmission Dynamics and Control Strategies Assessment of Avian Influenza A (H5N6) in the Philippines. Infectious Disease Modelling, 3(2018), 35-59.

[OIE] Office International des Epizooties. (2011). Update on Avian Influenza in

Animals (Types H5 and H7) [internet]. [diacu 2020 Desember 10]. Tersedia dari: http://web.oie.int/waHSI/reports/en_fup_0000011040_20110921_161632.pdf.

Ulfa, S.A. (2020). Analisis Kestabilan Model Penyebaran Penyakit Pada Tanaman Jatropha Curcas [skripsi thesis]. Surabaya (ID) : Universitas Airlangga.

101