Analisis Dinamika Model Penyakit Toksoplasmosis pada Populasi Kucing dan Manusia

Jurnal Matematika Vol. 11, No.2, Desember 2021, pp. 75-86

Article DOI: 10.24843/JMAT.2021.v11.i02.p138

ISSN: 1693-1394

Analisis Dinamika Model Penyakit Toksoplasmosis pada Populasi Kucing dan Manusia

Riza Rusdiani

Kampus IPB, Jl. Raya Dramaga, Babakan, Kec. Dramaga, Kota Bogor, Jawa Barat 16680 e-mail: [email protected]

Ali Kusnanto

Kampus IPB, Jl. Raya Dramaga, Babakan, Kec. Dramaga, Kota Bogor, Jawa Barat 16680 e-mail: [email protected]

Paian Sianturi

Kampus IPB, Jl. Raya Dramaga, Babakan, Kec. Dramaga, Kota Bogor, Jawa Barat 16680 e-mail: [email protected]

Abstract: Toxoplasmosis is a disease that is identical to cats. This disease is caused by the parasite Toxoplasma gondii. In this study, a mathematical model of the spread of toxoplasmosis was reviewed with various population size. In this study, model construction, fixed point analysis and parameter sensitivity analysis were carried out. From the sensitivity analysis, it is shown that the cat transmission rate from a susceptible cat population to an infected cat population (horizontal transmission rate) and the probability of a susceptible cat born from an infected cat (vertical transmission rate) are found as sensitive parameters on production number (ℛ₀). Decreasing the horizontal transmission rate and an increase value of the vertical transmission rate can reduce the value of ℛ₀. A decrease in the value of ℛ₀, results in a disease-free state will be achieved more quickly so that the disease is under control.

Keywords: cat, Toxoplasmosis, horizontal transmissions, vertical transmissions

Abstrak: Toksoplasmosis merupakan penyakit yang identik dengan kucing. Penyakit ini disebabkan oleh parasit Toxoplasma gondii. Pada penelitian ini, ditinjau model matematika penyebaran penyakit toksoplasmosis dengan menggunakan ukuran populasi yang bervariasi. Dalam penelitian ini dilakukan konstruksi model, analisis titik tetap dan analisis sensitivitas parameter. Dari analisis sensitivitas ditunjukkan bahwa laju transmisi kucing dari populasi kucing rentan ke populasi kucing terinfeksi (laju transmisi horizontal) dan peluang kucing rentan lahir dari kucing yang terinfeksi (laju transmisi vertikal) adalah parameter yang sensitif terhadap bilangan reproduksi dasar (ℛ₀). Penurunan laju transmisi horizontal dan peningkatan laju transmisi vertikal akan menurunkan nilai ℛ₀. Penurunan nilai ℛ₀, berakibat keadaan bebas penyakit akan tercapai lebih cepat sehingga penyakit terkendali.

Kata Kunci: kucing, Toksoplasmosis, transmisi horizontal, transmisi vertikal

• 1.    Pendahuluan

Toksoplasmosis merupakan penyakit yang dapat diderita manusia dan semua hewan berdarah panas seperti domba, kucing, dan kuda (Hill, Chirukandoth, & Dubey, 2005). Penyakit ini disebabkan oleh Toxoplasma gondii (T.gondii). T.gondii merupakan organisme bersel satu yang hidup sebagai parasit. Penyakit ini menyebar dari hewan ke manusia melalui makanan atau minuman yang telah terkontaminasi oleh ookista (Pereira, Franco, & Leal, 2010).

Prevalensi toksoplasmosis di Indonesia berkisar antara 2%-88% yang tersebar di seluruh kepulauan yang ada di Indonesia (Aditama, Nurjazuli, & Dina, 2016). Berdasarkan hal tersebut, dibentuklah suatu model matematika untuk memodelkan strategi pencegahan dan pengendalian terhadap penyakit ini dengan bantuan simulasi numerik.

Pada penelitian ini dikembangkan model penyakit toksoplasmosis pada populasi kucing dan manusia yang sebelumnya telah dikembangkan oleh Pei et al.(2018). Perbedaan penelitian ini dengan penelitian sebelumnya yaitu pada pemisahan model menjadi dua model. Model I menggunakan asumsi kelahiran pada populasi kucing dapat terjadi pada populasi rentan dan terinfeksi dan anaknya akan sesuai dengan induknya, sedangkan model II menggunakan asumsi kelahiran pada populasi kucing hanya dapat terjadi pada populasi rentan dan peluang bayi yang lahir dalam kondisi sehat dari ibu yang terinfeksi, serta peluang kucing lahir dalam keadaan rentan tidak diketahui. Penelitian ini bertujuan untuk mengamati pengaruh perubahan nilai parameter terhadap dinamika model.

• 2.    Metode Penelitian

Metode yang digunakan dalam penelitian ini adalah dengan melakukan rekonstruksi model yang telah dikembangkan oleh Pei et al.(2018) dan mengembangkannya dengan membuat dua jenis model. Langkah berikutnya adalah menentukan bilangan reproduksi dasar (K₀), melakukan analisis sensitivitas terhadap parameter-parameter model, serta mengamati pengaruh parameter pada dinamika populasi kucing dan manusia dengan simulasi numerik.

Bilangan reproduksi dasar (K₀) merupakan nilai harapan terjadinya infeksi per satuan waktu pada suatu populasi yang mengakibatkan seluruhnya bersifat rentan yang dihasilkan oleh satu jenis individu yang sudah terinfeksi. K₀ dalam penelitian ini ditentukan dengan menggunakan metode yang dikenalkan oleh Driessche & Watmough (2008) yaitu mengkonstruksi suatu matriks yang berasal dari subpopulasi-subpopulasi yang menyebabkan infeksi saja. Matriks tersebut dikenal dengan “the next generation matrix”. Nilai K₀ merupakan nilai eigen tak negatif terbesar dari matriks tersebut.

Kondisi yang mungkin dari bilangan reproduksi dasar menurut Driessche & Watmough (2008) adalah

• 1.    Jika K₀ < 1 maka jumlah individu yang terinfeksi akan menurun pada generasi, sehingga penyakit tidak akan menyebar.

• 2.    Jika K₀ > 1 maka jumlah individu yang terinfeksi akan meningkat pada generasi, sehingga penyakit akan menyebar.

Analisis sensitivitas merupakan analisis yang digunakan untuk memeriksa perubahan

K₀ yang terjadi akibat adanya pengaruh perubahan nilai parameter pada model dan digunakan untuk menunjukkan parameter yang paling berpengaruh dalam menentukan hasil analisis model. Dalam analisis sensitivitas, indeks sensitivitas bilangan reproduksi

dasar K₀ yang bergantung pada parameter p didefinisikan pada persamaan (1) berikut

Ko _ ^dK0   ^p

(1)

^Kp    dp ×K₀

Indeks sensitivitas y^o digunakan untuk menunjukkan perubahan relatif pada bilangan

reproduksi K₀ ketika parameter p diubah (Natkul, James, & Jim, 2008). Indeks sensitivitas bertujuan untuk melihat parameter-parameter terhadap perubahan nilai K₀ • Indeks sensitivitas yang bernilai positif menunjukkan bahwa apabila parameter p ditingkatkan dan parameter yang lainnya dibuat tetap, maka akan meningkatkan nilai K₀ dan setiap penurunan nilai parameter p menyebabkan nilai K₀ menurun.

• 3.    Hasil dan Pembahasan
  
  Perumusan Model I

Populasi manusia terbagi menjadi tiga kelas yaitu S_h populasi manusia rentan (Susceptible), Ih populasi terinfeksi (Infected), dan R populasi yang pulih atau sembuh dari toksoplasmosis (Recovered). Sedangkan populasi kucing terbagi menjadi dua kelas yaitu S_c populasi kucing yang berisiko tertular penyakit (Susceptible) dan I_c populasi kucing yang terinfeksi parasit (Infected). Total populasi manusia dilambangkan dengan Nh dan total populasi kucing dilambangkan dengan N_c. Secara skematis, penyebaran penyakit toksoplasmosis dapat digambarkan dalam diagram kompartemen pada Gambar 1 berikut.

Gambar 1. Diagram kompartemen penyebaran penyakit toksoplasmosis

Berdasarkan diagram kompartemen pada Gambar 1 diperoleh sistem persamaan (2) sebagai berikut:

dS_h(f) dt dI_h(t) dt dR

. _   „ „    Ic(t)

= ^μh^h(^t) ^{- μ}h(^{1- p}h^)Ih^{(t) - kS}h^{(t) -} βh^sh(^t TTTT?, ^c^(t)

„ „ ' ' Ic(t)

= ^β*^S*^{(t)       + μ}h(^{1 - p}h^)Ih^{(t) - kI}h^(t'^{) -} Y¹h(^t),

^c^(t)

-^ = γlh(t) - kR⁽t), Nh(f) = S_h(f) + I_h(f) + ^R(t),

(2)

dSc(f) dt dI_c(t) dt

I_c(t)

= μ_cp_cI_c(t) - βcSc(t) N~φ,

I_c(t) =^tv

-

μ_cPcic(t),

N_c(t) = S_c(t) + I_c(t),

di mana konstanta μ_h, μ_c, p_h, p_c, k, γ, β_h, β_c > 0. Selanjutnya didefinisikan,

Si(t>    m-!*®.    ^ R(t

'   N_h(t)     ^y(t) W_ft(t)' ^Z(t)   Λ⅛(t)'

m  SAD          Ic(t)

^u(^t)=wi-   ^v(^t) = w-y

dan diketahui bahwa,

x(t) + y(t) + z(t) = 1 dan u(t) + v(t) = 1.

Selanjutnya, sistem persamaan (2) dapat disederhanakan menjadi :

{

x(t) = Vh- Vh(ι - Ph)y(t) - χ(t)(μ_h + β_h(1 - u⁽t)), ^y(t) = βh×(t)(1 - u⁽t)) + y(t)(μh(1 - Ph) -⁽Y + Vh)) ^u(t) =       μ_cP_c(1 - u(f)) - β_cu(t)(1 - u⁽t)),

(3)

dengan μh, μ_c,Ph,P_c,k,γ, βh, β_c > 0. Deskripsi parameter pada (3) akan disajikan pada Tabel 1.

	Tabel 1. Deskripsi parameter dari model
Parameter	Deskripsi
βh βc Y	Laju transmisi individu dari populasi manusia rentan ke populasi manusia terinfeksi. Laju transmisi kucing dari populasi kucing rentan ke populasi kucing terinfeksi. Laju transmisi individu dari populasi manusia terinfeksi ke populasi manusia yang telah pulih atau sembuh.
μh μc Ph	Tingkat kelahiran manusia. Tingkat kelahiran kucing. Diasumsikan sama dengan tingkat kematian alaminya. Peluang bayi yang baru lahir dari seorang ibu yang terinfeksi toksoplasmosis dalam keadaan sehat.
Pc k χ(t) y(t) z(t} u(t) V (t)	Peluang kucing rentan lahir dari kucing yang terinfeksi toksoplasmosis. Tingkat kematian alami manusia. Proporsi populasi manusia yang rentan pada waktu t. Proporsi populasi manusia yang terinfeksi pada waktu t. Proporsi populasi manusia yang telah pulih atau sembuh pada waktu t. Proporsi populasi kucing yang rentan pada waktu t. Proporsi populasi kucing yang terinfeksi pada waktu t.

Penentuan Titik Tetap

Berdasarkan (3) diperoleh dua jenis titik tetap, yaitu titik tetap bebas penyakit dan titik tetap endemik. Titik tetap bebas penyakit E₁(x,y,u) = (1,0,1) dan titik tetap endemik adalah ^E₂⁽x.y,u) = (x2.y2.u2). dengan u_i=^. χ_i=-^-+μ^^ 2  _________β-μ-(^1-u'²)_________

^y2   βħ(1-U*²)(γ+μħ)+μħ(γ+Pħμhy

Bilangan Reproduksi Dasar

Bilangan reproduksi dasar (K₀) merupakan nilai eigen maksimum tak negatif dari the next generation matrix, dan didapat

^Ko =     ■

^μcUc

Teorema 1. Jika K₀ < 1 maka titik tetap bebas penyakit E₁ bersifat stabil asimtotik lokal.

Jika K₀ > 1 maka tidak stabil.

Bukti. Untuk membuktikan Teorema 1, dilakukan linearisasi sistem persamaan (3) di titik

E₁ yang akan menghasilkan matriks Jacobi sebagai berikut:

J-^Ph  -^Ph^{(1 -} Ph)

βh

^-βh -^Pc^Pc ^{+ β}c

)

Je₁ = ∖  0    -⁽y + PhPh)

00

Nilai eigen untuk titik tetap bebas penyakit E₁ diperoleh dengan menyelesaikan persamaan karakteristik berikut :

∣Jei-ai∣ = 0.

atau

I^-Ph^{-A    -}Ph(^1-ph)         ^βh      I

^{0     -}(^{γ + p}hPh) ^{- A       -β}h      = 0.

I 0           0        -PcPc+β_c-A

Diperoleh tiga nilai eigen dengan dua nilai eigen bernilai negatif yaitu A₁ = —Ph, A₂ = —Y — PhPh dan nilai eigen lainnya yaitu A₃ = -P_cp_c + β_c. Jika K₀ < 1 maka A₃ < 0.

Selanjutnya, jika K₀ > 1 maka terdapat nilai eigen yang bernilai positif yaitu A₃.

Teorema 2. Titik tetap endemik positif E₂ bersifat stabil asimtotik lokal jika K₀ > 1.

Bukti. Untuk membuktikan Teorema 2, dilakukan linearisasi sistem persamaan (3) di titik

E₂ yang akan menghasilkan matriks Jacobi sebagai berikut:

	/-ph-βh(1-u2)  -Ph(1-Ph)        βhx2      \
jE2 =	I    βh(1 - u2)     -(y + PhPh)         -βhx2        . \      0             0      -PcPc-βc + 2βc⅛/

Nilai eigen untuk titik tetap endemik E₂ diperoleh dengan menyelesaikan persamaan

karakteristik berikut :

∣Je₂ -^a1∣=0.

atau

I(^-P-h ^{- β}h(^{1 - u}2)) ^{- a}    -^Ph^(1-ph)              ^βh^x2          I

^βh(^1-u2)        ⁽-^Y-^ph^Ph)^{-A           -β}h^x2>          = ^0.

I          0                    0         (-PcPc-βc + 2βcU*₂)-A∖

Persamaan karakteristik di atas dapat ditulis sebagai berikut:

^((-PcPc ^{- β}c ^{+ 2β}c^u2) ^{- a}A^{a2 + a}1^{A + a}2^] = 0.

dengan,

aι=Ph+ βh(1 -u2)+γ + PhPh.

^a2 = ^ph^βh^{(1 - P}h^{)(1 - u2) +} (^ph ^{+ β}h(^{1 - u2))(y + P}h^Ph).

Diperoleh tiga nilai eigen dengan satu nilai eigen bernilai negatif yaitu A₁ = P_cP_c — β_c. Jika K₀ > 1 maka A₁ < 0. Selanjutnya, dua nilai eigen lainnya ditentukan dengan menyelesaikan persamaan kuadrat berikut A² + a₁A + a₂ = 0. Persamaan ini harus

memenuhi kriteria a₁ > 0 dan a₂ > 0. Karena semua nilai parameter positif dan R₀ > 1, maka terbukti bahwa α₁ > 0 dan a₂ > 0 .

Perumusan Model II

Pada model II diasumsikan kelahiran pada populasi kucing hanya terjadi pada populasi yang rentan dan peluang bayi yang lahir dalam keadaan sehat dari seorang ibu yang terinfeksi (p^), serta peluang kucing rentan lahir(p_c) tidak diketahui. Berdasarkan asumsi

tersebut maka didapat sistem persamaan sebagai berikut:

dS_h(t) dt dI_h(t) dt dR

I_c(t)

= Ph^Nh⁽t) ^- μh¹h(t) ^- k^sh^{(t) - β}h^Sh^(t) TTTR, ^c^(t)

„ „     Ic(t)

= ^βh^Sh^(t'⁾ _N    ⁺ μh¹h(^t) ^- kl_h(t) ^- γl_h(t),

™c^(t)

-^ = Y¹h(t) — kR⁽t),

(4)

Nh(t) = ^Sh(f) ^{+ 1}h(^t) + ^R(t),

^ds(^t- = μcNc(t) - μcSc(t) - β_cS_c(t) ¹^

dt                                  N_c(t)

^dc(^t) = β_cS_c(t) ⅛(^t)- - μ_cI_c(t), dt     ^{cc c}   N_c(t)   ^cc

Nc(t) =Sc(t)+Ic(t).

Berdasarkan langkah-langkah seperti pada model I, sistem persamaan (4) dapat

disederhanakan menjadi:

x(t) =μh- μhy(t) - β_hχ(t)(ι - u⁽t)) - μ_hx(t), y (t) =        β_hx(t)(1 - u⁽t)) - γy(f),

f

(5)

^u(t) =    μ_c(1-u(t))-β_cu(t)(1-u(t)).

Penentuan Titik Tetap

Pada model II, dari sistem persamaan (5) diperoleh dua titik tetap, yaitu titik tetap bebas penyakit E₃(x,y,u) = (1,0,1) dantitiktetapendemikE₄(x, y, u) = (x*,y*,ub),dengan

• *                     ^βcγμn

x* = --------T--------—-------:--------:------.

• ^βc^βh^{γ - β}h^γμc ^{+ β}c^βh^μh ^{+ β}c^γμh ^{- β}h^μc^μh

• * ₌___________Ph(Ec-Vc)Vh___________

• ^b   PcPhY^-PhYVc⁺PcPhVh+PcYVh-PhVcVh

• * _μc

^ub   βc'

Bilangan Reproduksi Dasar

Bilangan reproduksi dasar (R₀) pada model II dari the next generation matrix (G') yaitu :

^0

βc

.

Hc

• 3.3 Simulasi Numerik

Nilai parameter yang digunakan terlihat seperti dalam Tabel 2 dan nilai indeks sensitivitas diberikan dalam Tabel 3. Simulasi numerik yang dilakukan menggunakan proporsi nilai awal x(0) = 0.5, y(0) = 0.3, z(0) = 0.2, n(0) = 0.45.

Tabel 2. Nilai parameter dari model

Parameter	Nilai Parameter	Sumber
Hh	0.233	(Aranda et al, 2008)
βh	0.0206	(Aranda et al, 2008)
Ph	0.9898	(Aranda et al, 2008)
y	0.000232	(Aranda et al, 2008)
k	0.00601	(Aranda et al, 2008)
Hc	0.066	(González-Parra et al, 2009)

Tabel 3. Nilai indeks sensitivitas dari model

Parameter	Indeks Sensitivitas Model I	Indeks Sensitivitas Model II
βc	1	1
HC	-1	-1
Pc	-1	-
Ph	0	-
Hh	0	0
βh	0	0
y	0	0
k	0	0

Berdasarkan Tabel 3 dapat disimpulkan bahwa parameter yang berpengaruh terhadap ^₀ untuk Model I dan Model II adalah β_c (laju transmisi toksoplasmosis dari populasi kucing rentan ke populasi kucing terinfeksi). Simulasi numerik dilakukan untuk melihat pengaruh parameter β_c ini terhadap dinamika populasi pada kedua model. Dengan menurunkan nilai parameter β_c dan memperhatikan perubahan nilai ^₀, akan mengakibatkan kondisi yang semula endemik menjadi bebas penyakit, seperti terlihat dalam Tabel 5.

Tabel 5. Perbedaan bilangan reproduksi dasar pada kedua model

Parameter βc	^0 Model I	^0 Model II
0.08	3.0303 > 1	1.21212 > 1
0.05	1.89394 > 1	0.757576 < 1
0.02	0.757576 < 1	0.30303 < 1
0.0005	0.0189394 < 1	0.00757576 < 1

Dengan menurunkan nilai parameter β_c, model II lebih cepat mencapai kondisi bebas penyakit dibandingkan model I. Selanjutnya untuk β_c = 0.02 pada model I dan β_c = 0.05 pada model II memiliki nilai ^₀ yang sama yaitu 0.757576, untuk perbedaan dinamika yang terjadi pada kedua model tersebut dapat dilihat pada Gambar 2.

Populasi Manusia Model I

Populasi Kucing Model I

Populasi Manusia Model II

Populasi Kucing Model II

Gambar 2 Dinamika populasi manusia dan kucing Model I dan Model II pada saat β_c = 0,05

Perbedaan pengaruh perubahan parameter β_c terhadap populasi manusia terinfeksi dapat dilihat pada Gambar 3 berikut.

WaMiHt)

Model I

Model II

Gambar 3 Dinamika populasi manusia terinfeksi Model I dan Model II dengan perubahan nilai β_c.

Selain itu, dilakukan simulasi penurunan nilai parameter β_c = 0.08 sebesar 20%, 50%, 80%, dan 100% pada kedua model. Hal ini bertujuan untuk melihat pengaruh populasi manusia terinfeksi jika parameter β_c diturunkan. Perbedaan pengaruh penurunan parameter β_c terhadap populasi manusia terinfeksi dapat dilihat pada tabel berikut:

Tabel 6. Hasil simulasi perubahan nilai parameter β_c = 0.08

Parameter βc	y(0 Model I	y(t) Model II
0.08	0.0564104	0.938658
0.064	0.0498107	0
0.04	0.0294451	0
0.016	0	0
0	0	0

Berdasarkan Tabel 6, jika β_c diturunkan 20%, 50%, 80%, dan 100% maka akan menyebabkan populasi manusia terinfeksi pada model II lebih cepat mencapai kondisi bebas penyakit dibandingkan dengan model I. Selanjutnya, dinamika populasi jika β_c diturunkan 20%, 50%, 80%, dan 100% dapat dilihat pada gambar berikut.

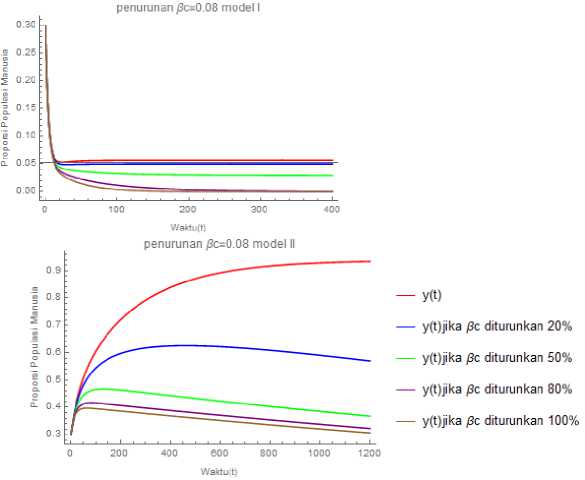
Model I

Model II

Gambar 1. Dinamika populasi saat β_c diturunkan 20%, 50%, 80%, dan 100% pada

kedua model

Pada Gambar 4 dapat dilihat dinamika populasi manusia terinfeksi pada model I akan mengalami penurunan hingga mencapai kondisi stabil, sedangkan pada model II akan mengalami peningkatan hingga mencapai kondisi stabil. Proporsi populasi manusia terinfeksi ini sesuai dengan hasil pada Tabel 6.

4. Kesimpulan dan Saran

Kesimpulan

Dalam penelitian ini dianalisis dua model penyakit toksoplasmosis pada populasi kucing dan manusia. Model I menggunakan asumsi kelahiran pada populasi kucing dapat terjadi pada populasi rentan dan terinfeksi dan anaknya akan sesuai dengan induknya, sedangkan model II menggunakan asumsi kelahiran pada populasi kucing dapat terjadi pada populasi rentan dan peluang bayi yang lahir dalam keadaan sehat dari seorang ibu yang terinfeksi (p_h) , serta peluang kucing lahir dalam keadaan rentan (p ') tidak diketahui. Kedua model yang dihasilkan dapat menggambarkan perilaku penyebaran penyakit.

Titik tetap bebas penyakit stabil asimtotik lokal terjadi saat bilangan reproduksi dasar kurang dari satu ^₀ < 1, sedangkan titik tetap endemik stabil asimtotik lokal pada kondisi bilangan reproduksi dasar lebih satu ^₀ > 1.

Hasil simulasi numerik kedua model juga menunjukkan bahwa penyakit akan punah atau tidak, bergantung pada parameter laju transmisi β_c. Semakin kecil laju transmisi β_c maka jumlah populasi manusia terinfeksi akan berkurang. Pada model II lebih cepat mencapai kondisi bebas penyakit dibandingkan Model I.

Saran

Penelitian selanjutnya diharapkan menambahkan parameter laju vaksinasi dan sterilisasi pada kucing sehingga penyebaran penyakit lebih sesuai dengan kondisi yang sebenarnya.

Ucapan Terima Kasih

Penulis mengucapkan terima kasih kepada Departemen Matematika IPB yang telah memberi dukungan financial terhadap makalah ini.

Daftar Pustaka

Aditama, N., Nurjazuli, & Dina, R.A. (2016). Determinan Lingkungan dan Perilaku Berhubungan dengan Terjadinya Penyakit Infeksi Toksoplasmosis di Wilayah Kota Semarang. Jurnal Kesehatan Masyarakat, 4(5), 67-76.

Aranda DF, Villanueva RJ, Arenas AJ, & González-Parra GC. 2008. Mathematical modeling of Toxoplasmosis disease in varying size populations. Comput Math with Appl. 56(3):690–696.

Driessche, V., & Watmough, J.( 2008). Further Notes on the Basic Reproduction Number.

Berlin Heidelberg: Springer-Verlag.

González-Parra, GC., Arenas AJ., Aranda, DF., Villanueva, RJ., & Jódar L. (2009). Dynamics of a model of Toxoplasmosis disease in human and cat populations. Comput Math with Appl, 57(10), 1692–1700.

Hill, DE., Chirukandoth, S., & Dubey, JP. (2005). Biology and epidemiology of Toxoplasma gondii in man and animals . Anim Heal Res Rev, 6(1), 41–61.

Natkul, C., James, MH., & Jim, MC. (2008). Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull Math Biol, 70(5), 1272–1296.

Pei, Y., Ji, X., Li, C., & Gao, S. (2018). Dynamics of a model of Toxoplasmosis disease in cat and human with varying size populations. Math Comput Simul, 144, 52–59.

Pereira, KS., Franco, RMB., & Leal, DAG. (2010). Transmission of toxoplasmosis (Toxoplasma gondii) by foods. Ed ke-1. Volume ke-60. Elsevier Inc.

86